基于神经元的多重分形分析在大模型神经元交互动力学中的应用
Neuron-based Multifractal Analysis of Neuron Interaction Dynamics in Large Models
发表年份:2025年
作者:Xiongye Xiao, Heng Ping, Chenyu Zhou, Defu Cao, Yaxing Li, Yi-Zhuo Zhou, Shixuan Li, Nikos Kanakaris, Paul Bogdan
作者机构:
南加州大学(University of Southern California)
加州大学河滨分校(University of California, Riverside)
期刊/会议:ICLR 2025(International Conference on Learning Representations)
1. 研究目的
当前对大模型涌现能力的研究,主要停留在外部观察:
关联规模与性能:发现模型参数越多(规模越大),在某些任务上的性能会突然变好。
黑箱评估:通过给模型做大量测试题(基准评测)来评估其能力。
这存在几个核心缺陷:
知其然不知其所以然:我们知道大模型有能力,但不知道这些能力是如何从模型内部产生的。
评估效率低:依赖外部测试,费时费力。
忽略结构:只关心模型“有多大”和“输出什么”,不关心其内部“结构是如何变化的”。
因此,本文的研究目的非常明确:开发一种新的方法,能够直接量化大模型内部结构的动态变化,并建立这种内部结构与“涌现能力”之间的直接联系。 他们要打开模型的“黑箱”,从结构的角度理解智能的涌现。
2. 方法
作者提出了一个名为 NeuroMFA(Neuron-based Multifractal Analysis) 的三步分析框架
第一步:将模型表示为一张图——神经元交互网络
为了能对AI的结构进行分析,我们要将一个LLM转化为一个神经交互网络(Neuron Interaction Networ,NIN)。NIN是一个有向图,图中的节点就是人工神经网络里的神经元,而连边上的权重则是原始权重的绝对值的倒数ωab = |wab|-1。具体操作如下:
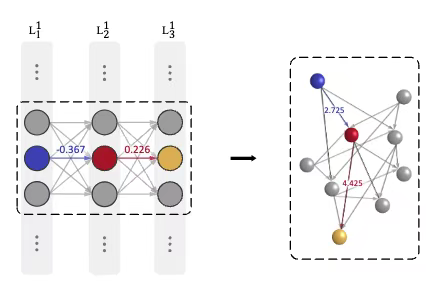
👍第1步:识别网络中的所有神经元
在一个典型的全连接前馈神经网络或Transformer的前馈层中:

👍第2步:定义边的权重(从“连接强度”到“距离”)
这是最关键的一步。在原始神经网络中,两层神经元之间有一个权重矩阵 W,其中的元素 wab 可以是正数或负数。
问题:传统的图分析工具(如最短路径算法)通常处理非负的边权重。负权重的存在会使得“距离”的概念失去意义。
解决方案:将原始的连接权重 wab 转换为一个非负的距离值 ωab。转换公式为:
![]()
参数解释:
∣wab∣:取绝对值,因为相互作用的强度不应为负。一个很大的负权重和一个很大的正权重,都表示两个神经元之间有非常强的相互影响。
p:是一个指数参数。在本文中,他们设定 p=−1。这意味着:
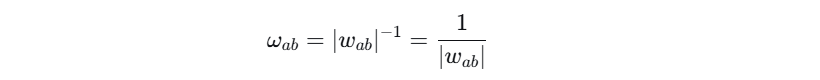
为什么这样设计?
这建立了一个直观的映射:
原始权重 ∣wab∣ 很大 → 连接很强 → 在图中,这两个节点应该“很近” → 距离 ωab 很小。
原始权重 ∣wab∣ 很小 → 连接很弱 → 在图中,这两个节点应该“很远” → 距离 ωab 很大。
通过这个转换,我们成功地将神经网络的连接强度,映射为了图论中的路径距离。
👍第3步:定义节点之间的距离(最短路径距离)
在NIN中,两个神经元 i 和 j 之间的距离 dij,定义为它们之间的最短加权路径。
关键点:这个路径可以跨越多个层。它不仅包括相邻层神经元之间的直接边,还包括通过中间层神经元连接的间接路径。
距离公式:
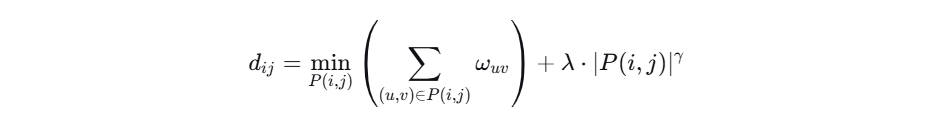
公式分解:
∑(u,v)∈P(i,j)v:这是路径 P(i,j)上所有边的权重(距离)之和。
∣P(i,j)∣:这是路径的长度(即经过的边的数量,或称“跳数”)。
λ 和 γ:是超参数,用于平衡路径总权重和路径长度的影响。引入路径长度项是为了防止算法总是选择跳数过多、虽然每跳距离小但总效率低下的路径。这类似于在现实世界中,换乘次数太多的路线即使总地理距离短,也可能不是最优路线。
算法:使用修改后的Dijkstra或Floyd-Warshall等最短路径算法,在允许跨层连接的前提下,计算所有节点对之间的 dij。
👍第4步:定义邻居关系
为了后续的分析,需要定义每个神经元 vi 的“邻居”。邻居不是根据层来定义的,而是根据上一步计算出的最短路径距离来定义的。

其中 d_threshold是一个预设的距离阈值。所有与 vi 的网络距离在这个阈值内的神经元,都被认为是它的邻居。这定义了一个基于网络拓扑结构的“局部区域”。
第二步:对这张图进行多重分形分析(NeuroMFA)——量化结构特征
这是最核心、最复杂的一步。分形通常描述一个物体在不同尺度下具有自相似性(如雪花)。多重分形则描述一个系统中同时存在多种不同的分形规律,即结构是异质性的。
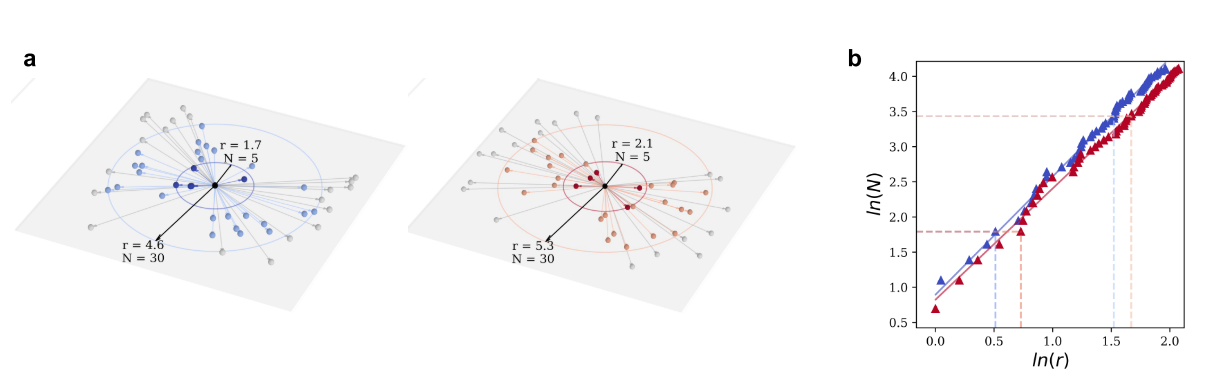
🍀做什么:分析NIN图中,以每个神经元为中心的局部区域的“质量”(即覆盖的其他神经元数量)如何随着“观测尺度”(即半径r)的变化而变化。
🍀具体操作(盒覆盖法扩展):
以某个神经元
v_i为中心,设定一个初始半径r。计算在这个半径形成的“球”内,包含多少个其他神经元,记为
N_i(r)。逐渐增大半径
r,记录一系列的(r, N_i(r))数据对。对这个关系进行拟合,发现它通常符合幂律关系:
N_i(r) ~ r^D。这里的D可以理解为该神经元局部的“分形维数”,描述了其周围空间的填充方式。
🍀引入多重分形:传统的分形分析只给整个网络一个平均的 D。但这会掩盖一个重要事实:网络中不同区域的疏密程度(即“奇异性”)是不同的。有的区域是“ hubs”(枢纽,非常稠密),有的区域是边缘(非常稀疏)。所以定义质量概率:对于神经元 vi 和尺度 r,定义其概率测度为:
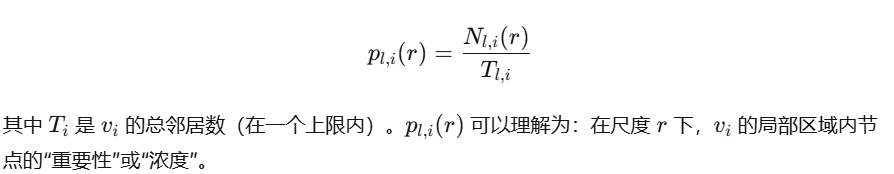
并通过一个叫“畸变因子”q的参数,来放大或缩小不同概率区域的影响。
🍀计算配分函数
Z_q(r):对所有神经元的 q 次方概率进行求和,得到配分函数,它是一个“加权计数器”:对不同区域进行有偏的统计,描述了在特定尺度 r 和畸变因子 q 下系统的整体状态。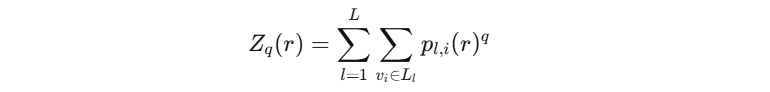
计算 Zq(r)的意义在于,它提供了一个系统性的、量化的方法来“扫描”或“探测”整个神经元交互网络(NIN),从而揭示其内部结构的异质性:尺度 r控制着放大倍率(看整体轮廓还是看局部细节)。
畸变因子 q 控制着聚焦方式(是重点关注密集区域还是稀疏区域)。
🍀计算质量指数
τ(q)与多重分形谱
文章发现:
Zq(r) 是微观性质的宏观体现:它本身是由成千上万个神经元的局部概率 pi(r)聚合(求和)而来的一个整体性、宏观的统计量。
τ(q) 是标度行为的量化:这个幂律关系表明,尽管网络结构复杂,但其统计行为在多个尺度上表现出规律性(标度不变性)。斜率 τ(q)就量化了在特定“聚焦方式”(q)下,这个宏观统计量随尺度(r)变化的速率。

通过计算配分函数 和 质量指数 最终可以得到两个关键的宏观结构指标:
不规则性度量 α₀:描述了网络中最常见的局部结构形态。α₀ 值降低,意味着整个网络的结构变得更规则、更有序。
异质性度量 w:描述了网络中存在的不同局部结构形态的范围。w 值增大,意味着网络的结构多样性在增加,出现了更多样化的连接模式。
1. 不规则性度量 α₀ 的获取
α₀ 的定义:它是多重分形谱 f(α) 取得最大值时所对应的 α 值。
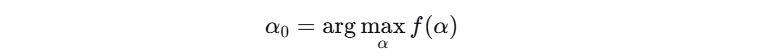
计算步骤:
得到完整的多重分形谱:通过之前的所有步骤,我们最终得到了一系列的 (α,f(α))数据对。这构成了一个连续的谱线,通常呈钟形(单峰)。
寻找峰值:在这条 f(α)谱线上,找到使 f(α)值最大的那个点。
读取横坐标:这个峰值点的横坐标 α 值,就是 α₀。
为什么 α₀ 能表示"最常见"的结构形态?
f(α)可以被理解为具有奇异性指数 α 的子集在系统中的"丰度"或"维度"。
因此,f(α)的最大值点,对应着在整个网络中出现得最频繁、最具代表性的那种局部结构形态。
α₀ 值的变化意味着什么?
α₀ 值高:意味着网络中最常见的局部结构是高度奇异、不规则的(例如,非常稠密或非常稀疏的极端区域)。
α₀ 值低:意味着网络中最常见的局部结构是相对平滑、规则、均匀的。
在训练过程中,α₀ 的降低 表明网络的结构正在从一种"混乱"的状态,朝着一种更有序、更稳定、更可预测的宏观状态演化。
2. 异质性度量 w 的获取
w 的定义:它是多重分形谱的宽度,即奇异性指数 α 的取值范围。
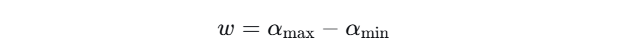
计算步骤:
确定 α 的范围:在计算出的多重分形谱 f(α)上,找到该谱线有效的 α 的最小值 αmin 和最大值 αmax。(在数值计算中,通常会设定一个阈值,例如 f(α)>0的区域,或者 f(α)大于其最大值某个百分比的区域)。
简单相减:计算两者的差值,即为谱宽 w。
为什么 w 能表示"结构多样性"?
α 值的范围直接对应着局部结构类型的范围。
αmin对应着网络中最稠密、最集中的区域(奇异性最强)。
αmax对应着网络中最稀疏、最分散的区域(奇异性最弱)。
因此,w 越大,说明网络中同时存在的结构类型越多,从极度稠密的"枢纽"到极度稀疏的"边缘",各种形态一应俱全。这体现了高度的异质性 或多样性。
w 值增大 表明在训练过程中,神经元之间的相互作用催生出了更多样化、更特化的连接模式,这是功能复杂化的重要结构基础。
之所以称为“多重分形分析”,是因为分析结果表明,神经元交互网络(NIN)的拓扑结构无法用一个单一的分形维数来刻画。相反,它是由一系列(即“多重”)不同的分形维数所共同描述的。
第三步:定义“涌现度”指标——将结构变化与能力关联
做什么:将第二步计算出的结构性指标,整合成一个单一的、可以衡量“涌现”的数值。
具体公式:
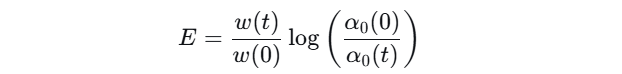
其中:w 表示异质性(谱宽度),
α0 表示规则性(谱峰值位置)。
公式解读:
w(t) / w(0):异质性增长因子。衡量从训练开始(0时刻)到当前时刻(t时刻),网络异质性的相对变化。比值>1表示异质性增加。< 1:表示异质性减少了。log[ α₀(0) / α₀(t) ]:规则性增长因子。衡量从开始到现在,网络规则性的相对变化。这是规则性(最常见结构形态 α0)变化的对数度量。由于α₀减小意味着规则性增加,所以这个对数值>0。使用比值是为了衡量相对变化。使用对数是为了将乘性变化转化为加性变化,并使指标对下降的幅度更敏感。同时,它确保了当规则性没有变化时(即 α0(t)=α0(0)),这一项为 0。E 值增大,直接表示模型内部结构正在同时朝着 “更多样” 和 “更有序” 的方向演化,作者将其定义为 “结构涌现”。
3. 主要结论与对应实验
结论一:大模型在训练过程中发生了显著的结构自组织,表现为异质性增加和规则性增强。
实验验证:
实验对象:Pythia模型套件(从14M到2.8B参数)。
分析方法:对模型在不同训练检查点(epoch)的NIN应用NeuroMFA,绘制其多重分形谱的演化图(如论文图5)。
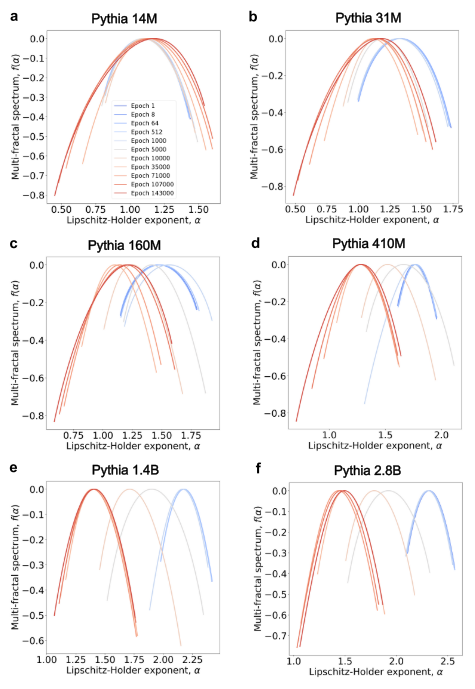
观测结果:
对于大于~100M参数的模型,随着训练进行,多重分形谱明显向左移动(表明 α0 减小,规则性增强)。
同时,谱的宽度 w 显著增加(表明异质性增加)。
对于小模型(14M, 31M),这种系统的、协调的结构变化不明显。
结论二:基于结构提出的“涌现度(E)”指标,与模型在标准基准测试上的性能表现正相关。
实验验证:
实验对象:Pythia-160M, 1.4B, 2.8B等模型在不同训练检查点。
分析方法:
计算每个检查点的涌现度 E。
在同一检查点上,用多个标准基准数据集(如LAMBADA, PIQA, ARC等)评估模型性能(准确率)。
将 E的变化曲线与性能变化曲线绘制在同一图中进行对比(如论文图6)。
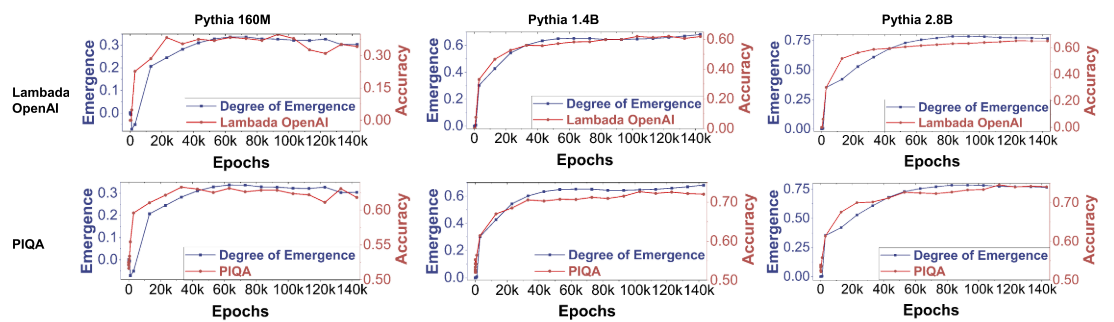
观测结果:E 的上升趋势与模型在多个任务上准确率的提升高度同步。这表明,纯粹从内部结构计算出的指标,可以可靠地反映模型外部能力的增长。
结论三:模型的“涌现能力”存在一个规模阈值,且“涌现度”随模型规模增大而对数增长。
实验验证:
实验对象:全系列的Pythia模型(不同参数规模)。
分析方法:
规模阈值:观察结论一的实验,发现小模型没有明显的自组织现象,因此也无法计算有意义的 E。
对数增长:在训练后期(如53,000 epoch),绘制不同规模模型的 “涌现度 E” 与其 “模型参数量” 的关系图(如论文图8)。
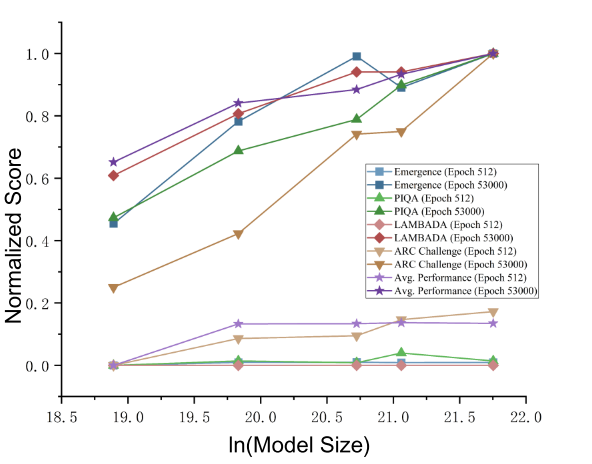
观测结果:E 与模型大小呈现出对数增长关系,这与许多关于模型规模扩展律的观察相符,从结构角度验证了“更大模型展现更强涌现能力”。
结论四:不同模型架构的“涌现潜力”不同,Transformer在自组织方面表现最优。
实验验证:
实验对象:Stable Diffusion(扩散模型)、ResNet-18、ResNet-152(CNN架构),并与规模相似的Pythia(Transformer架构)对比。
分析方法:对这些不同架构的模型应用相同的NeuroMFA,分析其多重分形谱(如论文图13, 14)。
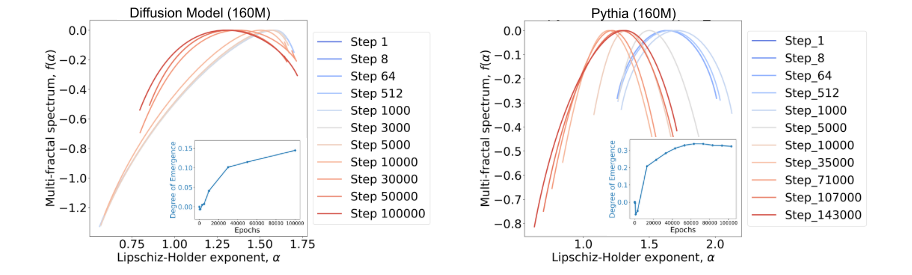
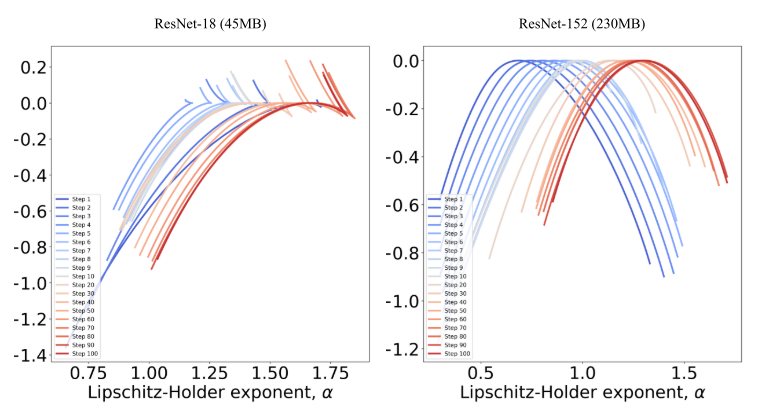
观测结果:
CNN(ResNet):谱图不规则,缺乏稳定的自组织迹象(ResNet-18几乎没有,ResNet-152有但不稳定)。
扩散模型:虽有多重分形结构,但其“涌现度”低于同等规模的Transformer模型。
结论:Transformer架构在训练中能形成最稳定、最复杂的自组织结构,这可能是其在NLP任务中表现出强大涌现能力的原因。
结论五:训练数据的质量影响模型的自组织过程和最终能力。
实验验证:
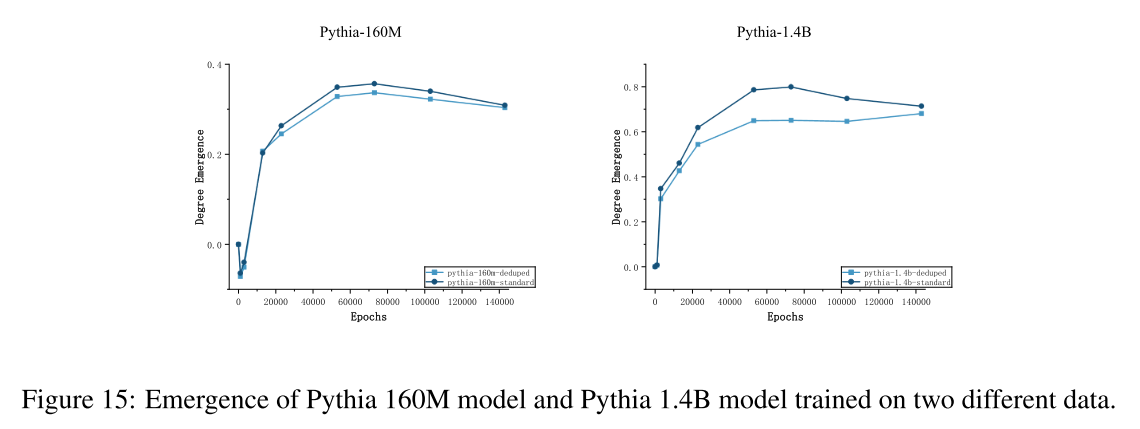
实验对象:Pythia-standard(标准数据集) vs. Pythia-deduped(去重数据集)。
分析方法:比较两种模型在训练过程中“涌现度 E”的增长曲线(如论文图15)。
观测结果:虽然结构自组织的“临界点”相似,但在标准数据集上训练的模型,其 E 的增长速率更快。这从结构角度解释了“数据质量”的重要性。
补充实验:使用污染数据微调BERT,结果显示其“涌现度”下降,与模型性能下降同步,反向证明了该指标的有效性。
这些实验从内部结构(结论1、4)、外部关联(结论2)、规模扩展(结论3)和训练要素(结论5)等多个维度,强有力地支撑了论文的核心论点:大模型的“涌现能力”可以通过其内部神经元交互网络的结构自组织(多重分形特性的演化)来量化、解释和预测。
