LDPC码译码算法--概率域BP译码算法和对数域BP译码算法

        置信度传播译码算法，简称为BP迭代译码算法，起源于在贝叶斯网络中的应用，后来就广泛应用到信号处理、通信网络和人工智能等方面。

        这种译码算法以Tanner图为基础，节点信息在这种连通图上反复传递更新，传递的路径就是图中的边，在这种信息的传递过程中，不断向着更可靠的方向更新各个节点的信息，那么在多次迭代之后，变量节点的值就会满足全部校验方程，这就是BP 迭代译码算法的思想。

        下图描述了BP迭代译码算法的过程。

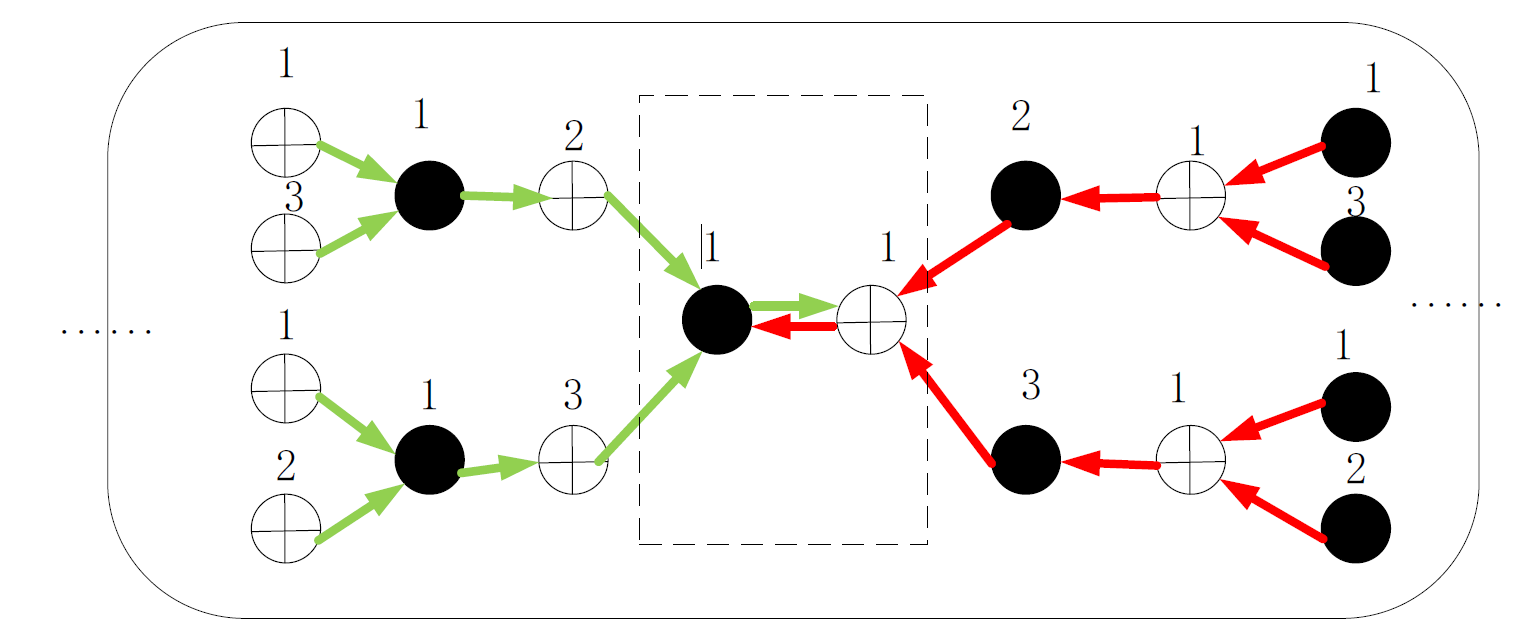
        BP 算法的运算就是不断进行着信息传递的过程，以一个变量节点为例，根据该节点参与的校验方程，所有与之相连的校验节点都参与该变量节点信息的更新，同样的，所有与校验节点连接的变量节点也都参与该校验节点信息的更新。

        但是在信息的更新过程中不能发生一个校验节点信息的更新过程中包含的变量节点信息是由该节点更新的。如上图所示左侧的信息转移路线是校验节点传递给变量节点的路径，右侧描述的是变量节点传递信息给校验节点的信息转移，二者对称传递。
        上述说明的信息传递过程的约束在这个图中以变量节点1 和校验节点1 为例说明，黑色实心圆点1~3 代表变量节点，带加号的白色圆圈1~3 为校验节点，那么变量节点传递给校验节点的信息是来自于标号2 和3 的校验节点，并不包含1，同样的校验节点传递给变量节点的信息也不能来自标号为1 的变量节点。

        保证每次信息的传递和转移都这样的进行。运算完成一次迭代后，对后验概率进行硬判决，判决为0、1 比特。下面将对BP 迭代译码算法进行描述，下表为相关参数。

        概率域上BP 算法可以表示为如下步骤：

1.初始化

        迭代次数为 1

2.校验节点更新

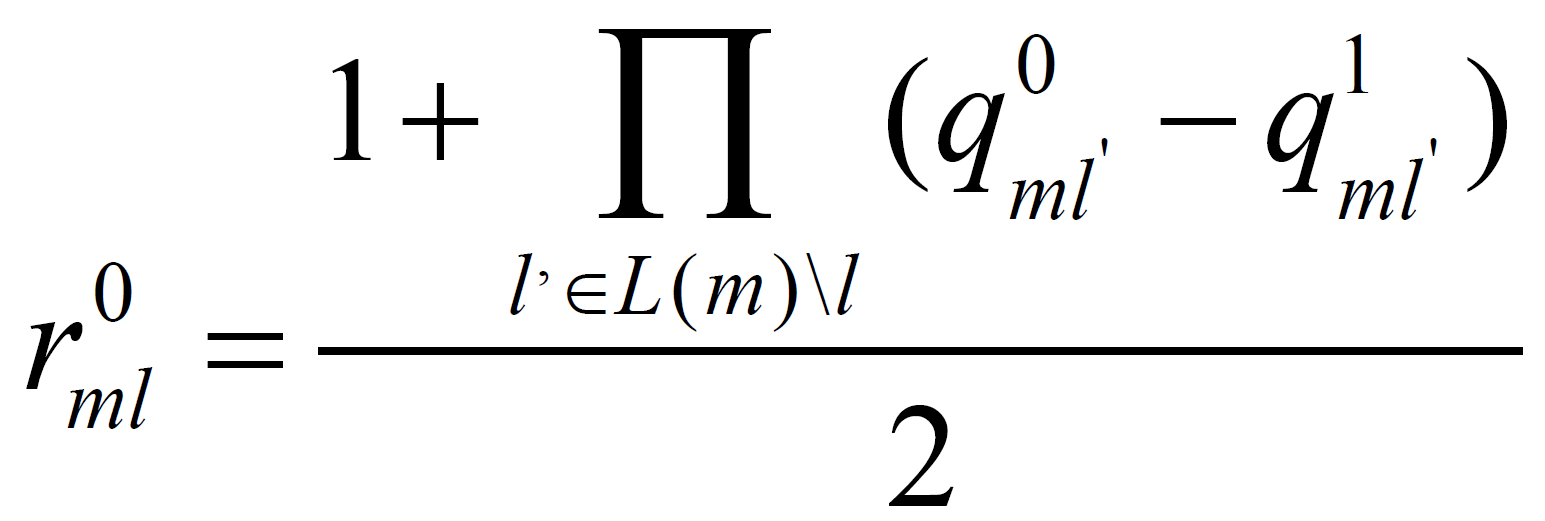
3.变量节点更新

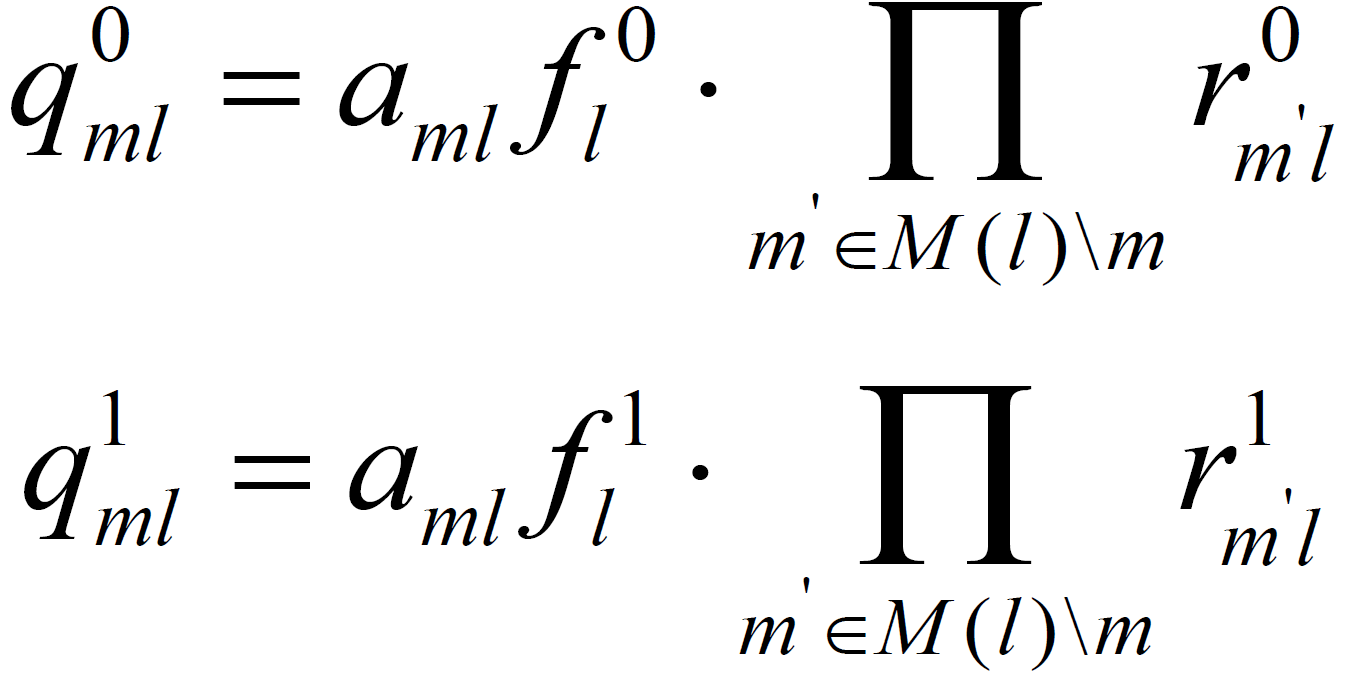
        其中，取值使得。

4.似后验概率更新和比特判决

，迭代次数为 1
        其中的取值使。若，则判决，否则判决。

5.停止译码

        若，或者迭代的次数已经超出了设定的最大迭代次数，跳出译码迭代，输出；不满足以上两个条件那么将当前的迭代次数自加，继续译码迭代过程，进入步骤2。
        在上面我们描述了BP迭代译码的算法过程，可以发现在整个算法过程中，存在指数运算以及大量的乘法、除法运算，这对于硬件实现来说，十分困难，而且除法运算会造成数据不稳定的情况。

        所以需要消除这种运算，根据信息论中的理论，可以将概率采用取对数的方法，用似然比代替概率信息，将这种概率域的运算变成对数域的加减，这就是对数域BP(LLR BP)算法，这样的操作不仅简化了运算，而且使表达式也更加简洁，并且也没有性能的损失。这种操作消除指数运算，将大量的乘除法转换为加减法运算，大大化简了整个运算过程。下面描述概率域BP 迭代译码算法过程。
        随机变量x的对数似然比L(x)为：

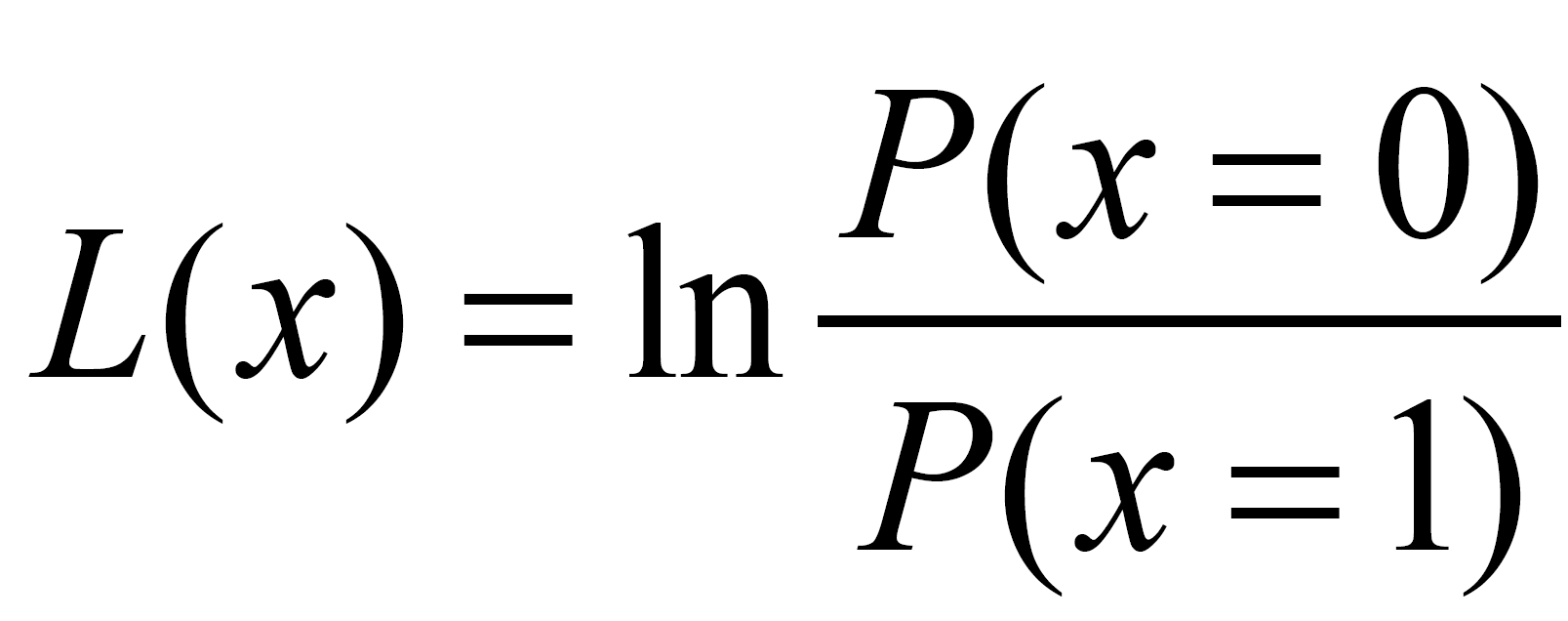
        根据上式的定义，则信道初始信息、校验节点传向变量节点的信息、变量节点传向校验节点的信息和变量节点搜集到的全部信息可以用下式表示。

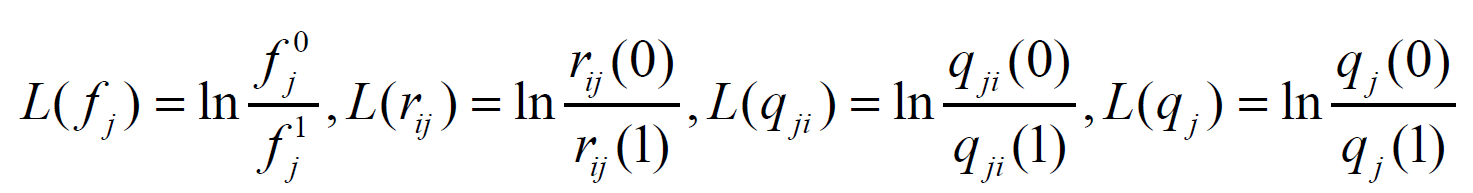
        对应的对数域上的BP 迭代译码算法步骤如下：

1.初始化：

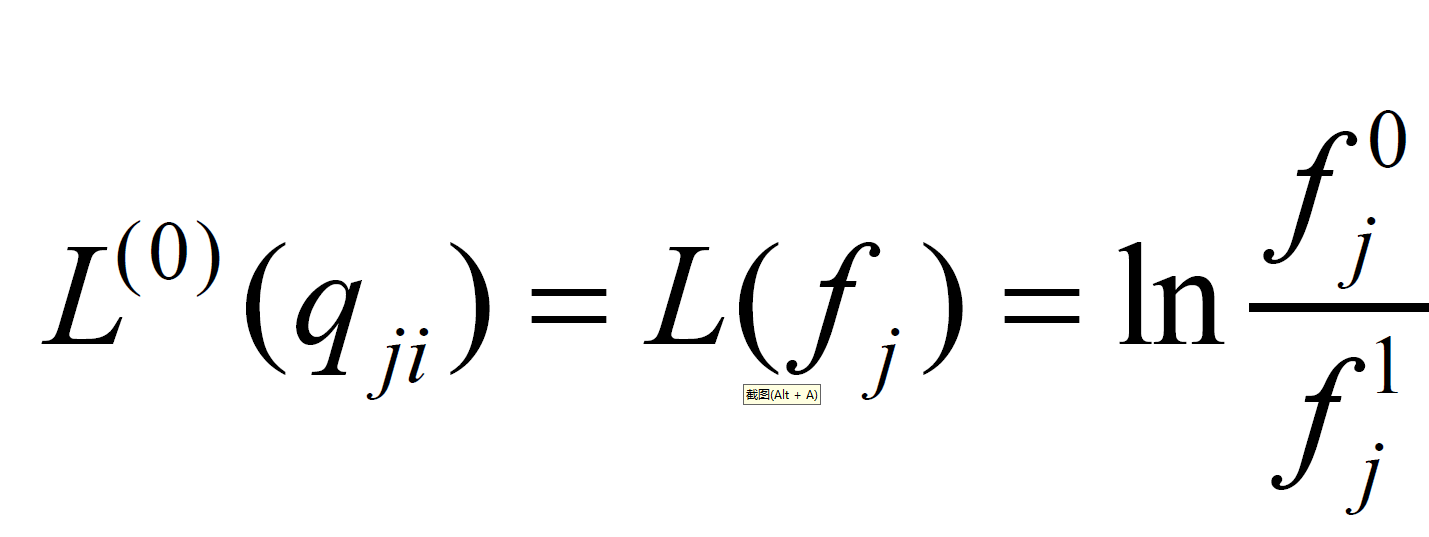
2.校验节点的更新：

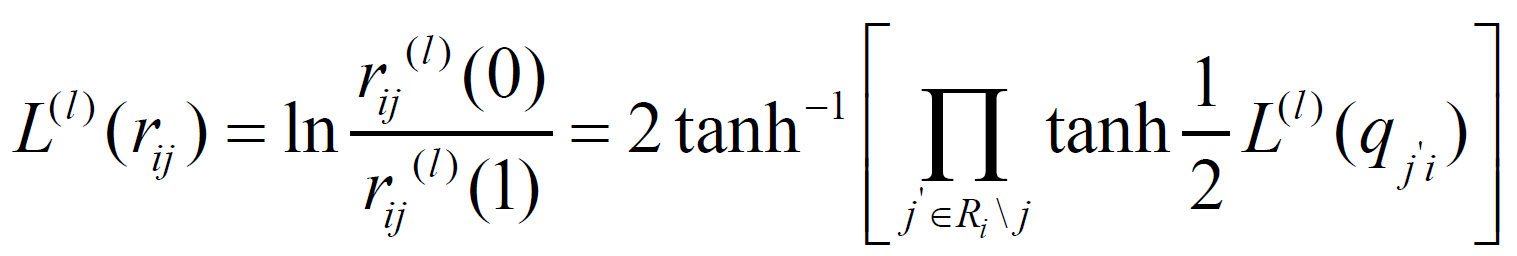
3.变量节点更新

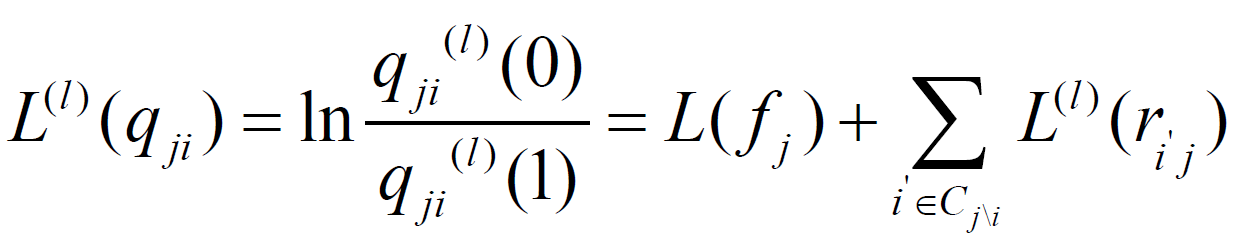
4.后验概率信息更新和译码结果的比特判决：

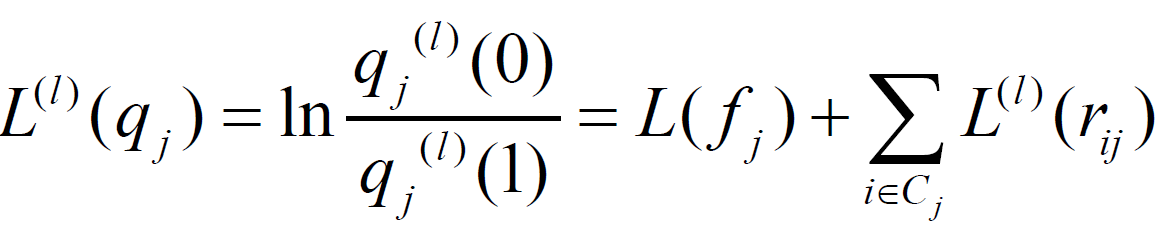
        如果 ,则判决，否则判决。

5.停止译码：

        若，或者迭代的次数已经超出了设定的最大迭代次数，跳出译码迭代，输出；不满足以上两个条件那么将当前的迭代次数自加，继续译码迭代过程，进入步骤2。
        根据以上的算法过程发现在对数域的运算已经不存在乘除法运算将其转换为对数域的加减法，大大降低了实现的难度。