当前位置：首页 > news >正文

卷积运算全解析：从原理到MATLAB实现

news 2025/10/29 7:31:59

1.简介

2.定义

3.实例理解

4.matlab代码实现

5.参考资料

本文主要记录了对卷积运算过程的理解，方便记忆并在日后中使用卷积。

1.简介

卷积是两个函数之间的一种数学运算，常用于信号处理、图像处理、系统分析等领域。卷积运算通过输入函数与另一个函数（通常被称为卷积核或滤波器）进行结合，生成一个新的函数。这个过程可以看作是一个系统对输入信号的“加权平均”或“平滑”过程。

2.定义

卷积在连续时间和离散时间下的定义：

连续时间： $y(t) = (f*g )(t) = \int_{-\infty}^{\infty} f(\tau) \, g(t - \tau) \, d\tau$

离散时间： $y[n] = (x* h)[n] = \sum_{k=-\infty}^{\infty} x[k] \, h[n - k]$

卷积的结果可以从两方面来理解：

系统响应：在系统理论中，卷积是描述线性时不变系统（LTI系统）响应输入信号的一种方式，系统的输出由输入信号与系统的脉冲响应卷积得到。
反映信号的历史影响：当前时刻的输出是过去所有时刻输入信号的加权总和，权重由卷积核决定。

3.实例理解

第二种理解方便我们记忆卷积的公式，当前时刻的卷积的结果是过去所有时刻输入信号的加权总和。用离散时间的卷积公式来举例子，卷积结果的变量是n,在离散时间中n表示为节拍，可以理解为数电中的时钟。将n从0开始带入下面的式子：

$y[n] = (x* h)[n] = \sum_{k=0}^{\infty} x[k] \, h[n - k]$

会得到:

$y(0) = x(0) \cdot h(0)\\ y(1) = x(0) \cdot h(1) + x(1) \cdot h(0)\\ y(2) = x(0) \cdot h(2) + x(1) \cdot h(1) + x(2) \cdot h(0)\\ ...$

将上述的结果用下面的图来理解：

当节拍n=0时：

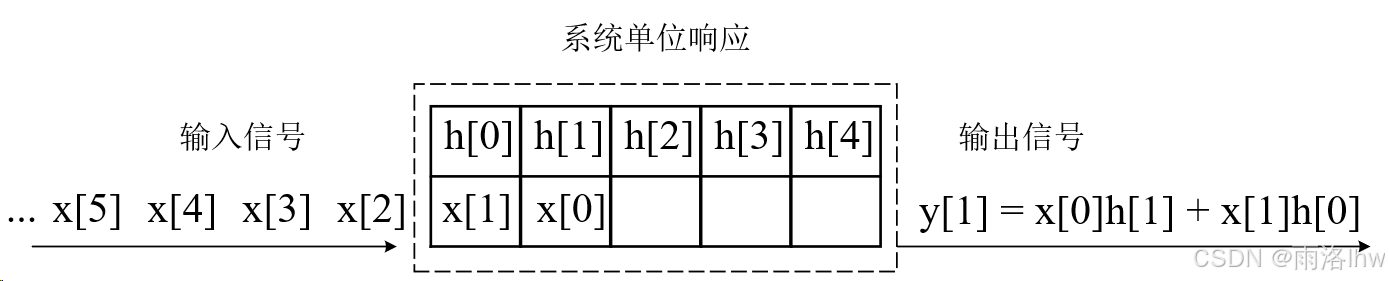
当节拍n=1时：

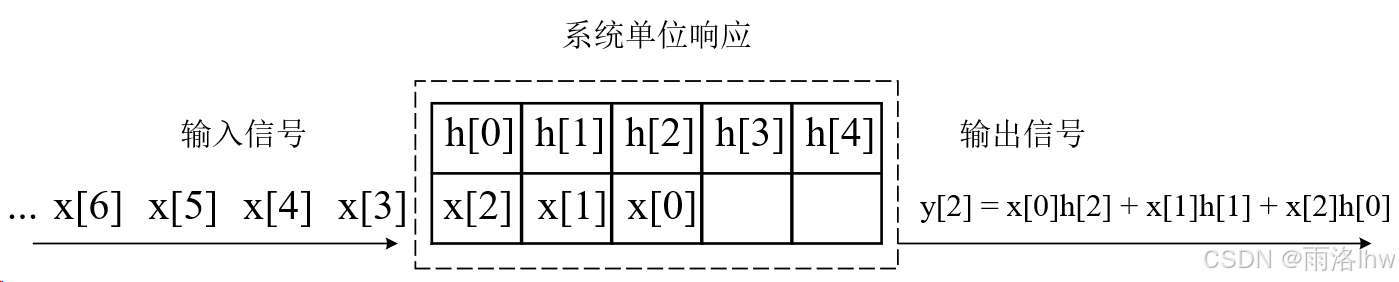
当节拍n=2时：

...

上面几幅图清晰地展示了定义中的计算过程。可以将 h[n]理解为一个不变的系统单位脉冲响应，无论信号何时输入，h[n]都不会发生变化。卷积的结果是当前时刻下，所有进入系统的输入信号与对应时刻的脉冲响应 h[n]的乘积之和。
例如，当n=0时，只有x[0]进入系统，此时卷积结果为 $y(0) = x(0) \cdot h(0)$ ；当n=1时，x[1]也进入系统并与h[0]对应，而 x[0]则随着节拍从h[0]传递到 h[1]，因此卷积结果为 $y(1) = x(0) \cdot h(1) + x(1) \cdot h(0)$ 。之后，随着时间的推移，信号依次进入系统，每一时刻的卷积结果是当前时刻下所有输入信号与其对应的h[n]的乘积之和。

上述的理解对于离散时间卷积的计算非常有帮助，但本质上还是遵循“反折—平移—相乘—相加（或积分）”的过程。只不过在这种方式中，通过对 x[n]进行翻折和平移（ $y[n] = (x* h)[n] = \sum_{k=0}^{\infty} h[k] \, x[n - k]$ ）来实现这一过程。实际上，这个过程与常规的卷积计算方式本质相同，因为卷积具有交换律，顺序的变化不会影响最终的结果。

反折是因为x[n]的表示方法为 {x[0],x[1],x[2],… }，即信号的方向与输入系统的方向相反。因此，必须将其反转为 {…,x[2],x[1],x[0]}，以便按照正确的顺序进入系统。图像中表现出来的就是波形的反折。
平移指的是信号随着节拍的推进逐步进入系统。在波形图中，这一过程表现为信号的平移。
相乘表示当前时刻下，所有进入系统的输入信号与对应时刻的脉冲响应 h[n]的乘积。
相加则是对各个时刻乘积的累积求和，从而得到最终的卷积结果。

连续时间： $y(t) = (f*g )(t) = \int_{-\infty}^{\infty} f(\tau) \, g(t - \tau) \, d\tau$ 的例子：

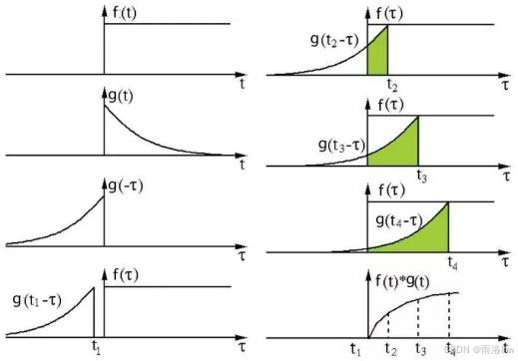
图中展示了将 g(t) 进行“反折—平移—相乘—积分”的过程，从而得到卷积的结果。 $g(t - \tau)$ 这里 t 为正值的原因在于“负负得正”。右移操作对应的是减法，而由于反折之后带有负号，因此两次负号相乘，结果为正值。
所以当两个信号进行卷积的时候可以将有限信号的波形进行反折，然后平移，两信号相乘积分。

4.matlab代码实现

卷积函数名称：C = Conv(a, b)

（1）C的区间长度为：序列a 的长度+序列b的长度-1；

（2）模拟两个连续时间信号卷积，需要额外地处理，才能得到真实的结果 Cr = C . Ts，这是因为卷积求的是面积和，而conv只能求取点数，所以用这个点数乘以采样间隔，从而近似等于这个面积；

离散时间形式：

%% //初始设置
% 清空工作空间，关闭无关页面
clc,clear,close all;% 绘图变量
font_size = 12; axis_size = 10; line_width = 2; legend_size = 12; marker_size = 6;
figure_width = 14; figure_height = 8; BiaValue = 0;%% //卷积-离散时间形式
% 信号x1
n1 = 0 : 1 : 4;
x1 = [0,2,4,6,8];% 信号x2
n2 = 0 : 1 : 4;
x2 = [1,3,5,7,9];% 卷积的结果
N = length(n1) + length(n2) - 1;
n = 0 : 1 : N-1;
y = conv(x1, x2);%% 绘图
figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(n1, x1, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 4])
ylim([0 10])
set(gca,'XTick',0 : 1 : 4)
set(gca,'YTick',0 : 2 : 10)
xlabel('节拍', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('离散时间信号x1[n]', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(n2, x2, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 4])
ylim([0 10])
set(gca,'XTick',0 : 1 : 4)
set(gca,'YTick',0 : 2 : 10)
xlabel('节拍', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('离散时间信号x2[n]', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
stem(n, y, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 10])
ylim([0 120])
set(gca,'XTick',0 : 1 : 10)
set(gca,'YTick',0 : 10 : 120)
xlabel('节拍', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
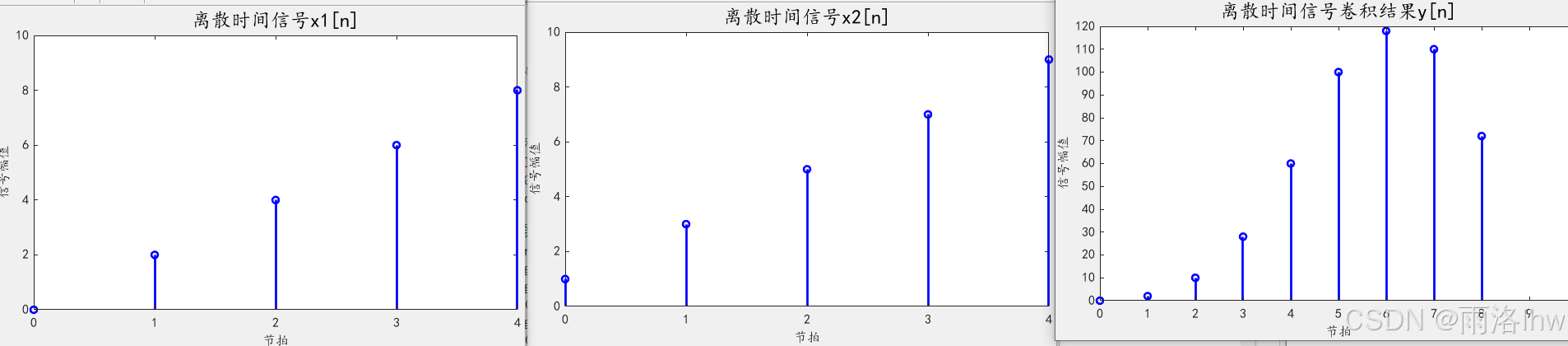
title('离散时间信号卷积结果y[n]', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')

x1 = [0,2,4,6,8]和x2 = [1,3,5,7,9]卷积结果如下：

连续时间形式：

%% //初始设置
% 清空工作空间，关闭无关页面
clc,clear,close all;% 绘图变量
font_size = 12; axis_size = 10; line_width = 2; legend_size = 12; marker_size = 6;
figure_width = 14; figure_height = 8; BiaValue = 0;%% //卷积-连续时间形式
% 以1ms短周期近似连续时间信号
Ts = 0.001;% 信号1：矩形函数
t1 = 0 : Ts : 5;
x1 = ((t1>0) - (t1>3));% 信号2：指数函数
t2 = 0 : Ts : 8;
x2 = exp(-t2);% 卷积结果
N = length(t1) + length(t2) - 1;
t = 0 : Ts : Ts*(N-1);y = conv(x1, x2);
% 注意！需要乘以Ts得到真实的卷积结果
y = y * Ts;  %注意这个结论%% 绘图
figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
plot(t1, x1, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 8])
ylim([0 1.6])
set(gca,'XTick',0 : 2 : 8)
set(gca,'YTick',0 : 0.4 : 1.6)
xlabel('时间 (s)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('连续时间信号x1(t)', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
plot(t2, x2, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 8])
ylim([0 1.6])
set(gca,'XTick',0 : 2 : 8)
set(gca,'YTick',0 : 0.4 : 1.6)
xlabel('时间 (s)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
title('连续时间信号x2(t)', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')figure
set(gcf,'Unit','centimeters','Position',[3 3 3+figure_width 3+figure_height]);
set(gca,'LooseInset',get(gca,'TightInset')+[BiaValue,0,0,0],'FontName','KaiTi','FontSize',font_size);
plot(t, y, 'b-', 'LineWidth', line_width)
set(gca,'FontSize',font_size,'FontName','KaiTi')
xlim([0 15])
ylim([0 1.6])
set(gca,'XTick',0 : 5 : 15)
set(gca,'YTick',0 : 0.4 : 1.6)
xlabel('时间 (s)', 'FontSize', font_size, 'FontName', 'KaiTi')
ylabel('信号幅值', 'FontSize', font_size, 'FontName', 'KaiTi')
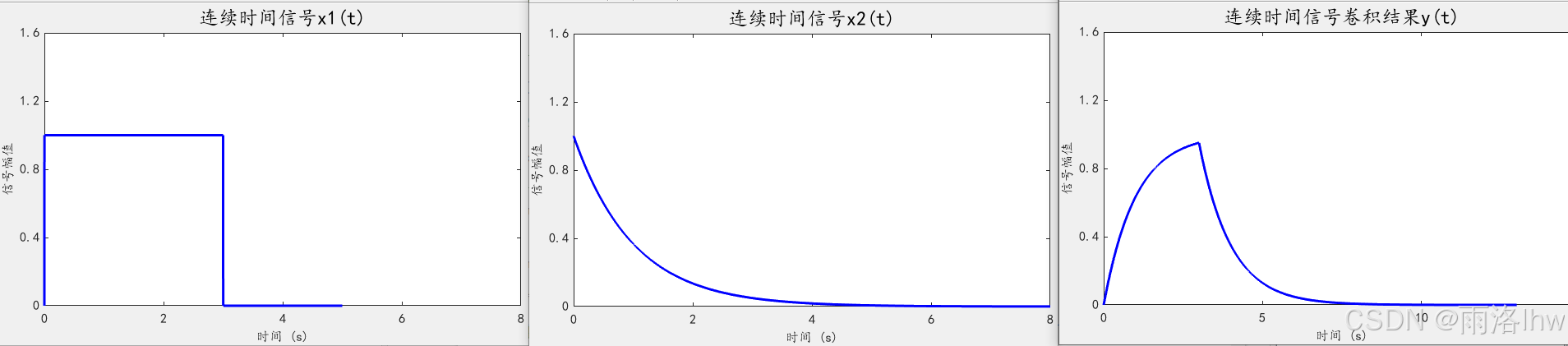
title('连续时间信号卷积结果y(t)', 'FontSize', font_size*1.5, 'FontName', 'KaiTi')

x1 = ((t1>0) - (t1>3))和x2 = exp(-t2);卷积结果如下：