【Swift】LeetCode 73. 矩阵置零

73. 矩阵置零

题目描述

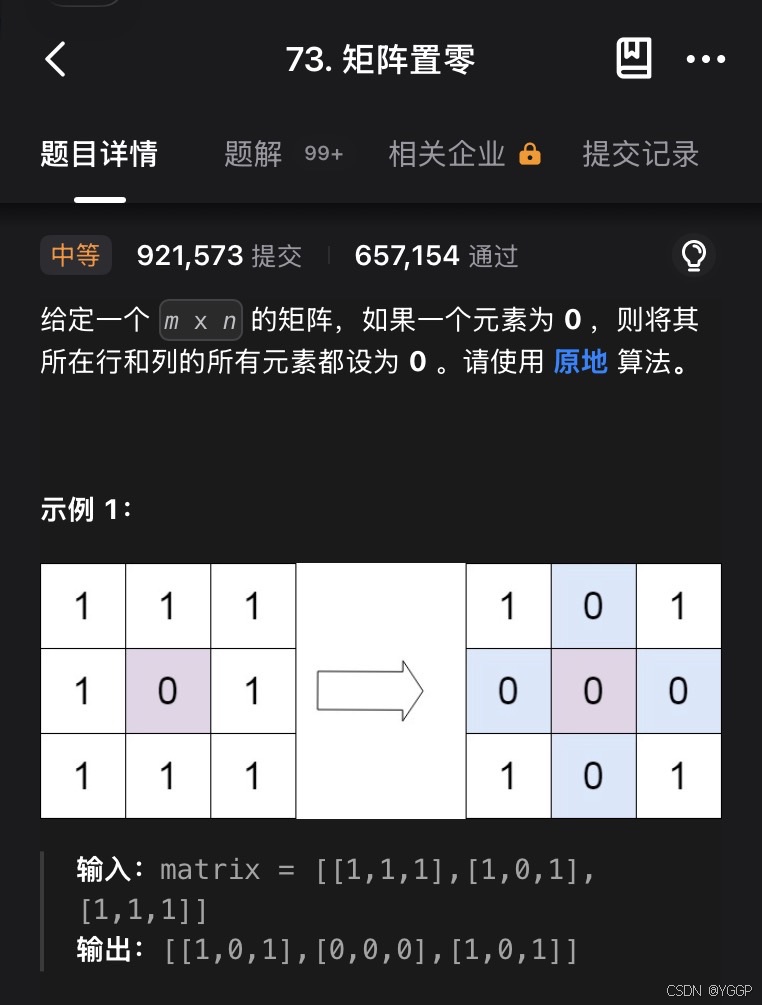
思路与 Swift 题解

由于这道题目已经要求需要使用原地算法，因此性能最好的算法应该是使用额外空间占用最少的算法。

解决这道题目的时候需要注意的是，我们不能够简单地通过一次遍历二维数组，令nums[i][j] == 0的第i行和第j列为零。理由非常简单，如果nums[0][0] == 0，我们接下来设置第零行第零列为零，那么整个数组最终都将会被置零。

我们可以通过两次遍历来解决这个问题。首先，我们第一次遍历二维数组，找到那些为零的值，并使用一种方式来标记这一行和这一列将来要被置为零。在第二次，我们不需要遍历整个数组，只需要置那些被标记为零的行和列为零即可。

问题归结为，我们通过什么方式来标记一行和一列将要被置为零。一个朴素的方式是新开两个向量（数组），长度分别为m和n，分别记录哪些行被标记为零以及哪些列被标记为零。该方式所占用的额外空间复杂度是m + n。

更简单的方式是，我们直接利用原数组的第零行和第零列。首先，我们找第零行当中是否有零，如果有的话，使用一个布尔值记录该行最后需要被置为零；对列同理。然后，我们跳过第零行和第零列，遍历整个二维数组，如果遇到nums[i][j] == 0，就置nums[0][j] = nums[i][0] = 0。再然后，基于第零行和第零列，我们置第一行及之后的相应行以及第一列及之后的相应列为零。最后，基于我们一开始维护的两个布尔值，置第零行和第零列为零。

基于上述方式，我们使用两个布尔值的额外空间复杂度，解决了这道题目。

完整的 Swift 题解是：

class Solution {func setZeroes(_ matrix: inout [[Int]]) {var m = matrix.countvar n = matrix[0].countvar col = false, row = falsefor i in 0..<m {if matrix[i][0] == 0 {col = truebreak}}for j in 0..<n {if matrix[0][j] == 0 {row = truebreak}}for i in 1..<m {for j in 1..<n {if matrix[i][j] == 0 {matrix[i][0] = 0matrix[0][j] = 0}}}for i in 1..<m {if matrix[i][0] == 0 {for j in 1..<n {matrix[i][j] = 0}}}for j in 1..<n {if matrix[0][j] == 0 {for i in 1..<m {matrix[i][j] = 0}}}if row {for j in 0..<n {matrix[0][j] = 0}}if col {for i in 0..<m {matrix[i][0] = 0}}}
}