当前位置：首页 > news >正文

归并排序和计数排序详解（非比较排序）

news 2025/10/29 6:32:39

1 归并排序

1.1 算法思想

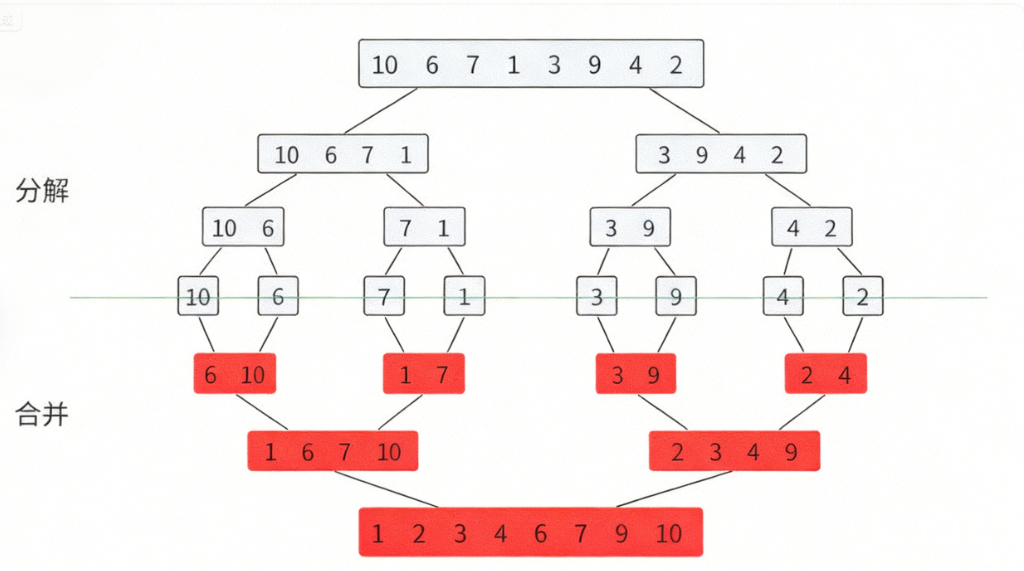
分解：先运用递归将序列进行分解直到只有一个元素
合并：使每一个子序列有序，再将两个有序的子序列合并成一个更大的有序子序列，直到整个序列有序

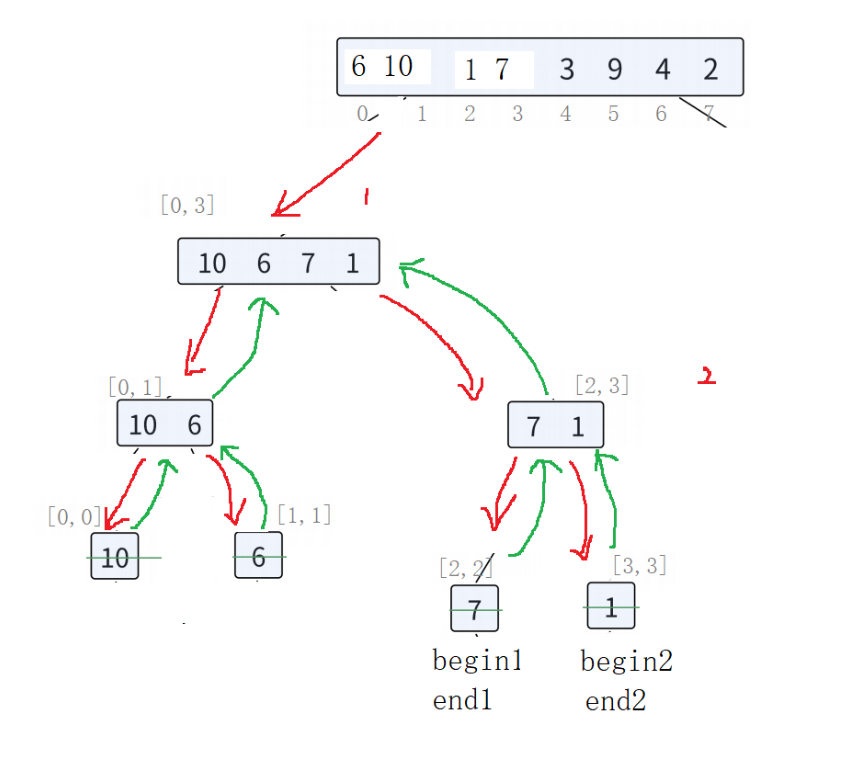
在这里插入图片描述

1.2 代码实现

#include<stdio.h>
#include<stdlib.h>
void MergeSort(int* arr, int left, int right,int* tmp)
{//归并排序if (left >= right){return;}int mid = (left + right) / 2;//确定中间位置划分成左右两个序列MergeSort(arr, left, mid,tmp);MergeSort(arr, mid+1, right,tmp);//这之后将其进行排序，将两个顺序序列连接起来int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = begin1;while (end1 >= begin1 && end2 >= begin2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin2 <= end2){tmp[index++] = arr[begin2++];}	while (begin1 <= end1){tmp[index++] = arr[begin1++];}//再将tmp里面数据返回arr中,从而实现arr数组的变化for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}
int main()
{int arr[] = { 2,7,3,9,8,5,6,1,4 };int len = sizeof(arr) / sizeof(arr[0]);int* tmp = (int*)calloc(len, sizeof(int));MergeSort(arr, 0, len - 1,tmp);for (int i = 0; i < len; i++){printf("%d ", arr[i]);}free(tmp);return 0;
}

2 计数排序

计数排序是一种非比较排序(不是元素之间通过比较大小来确定位置关系)，又称为鸽巢原理，是对哈希直接定址法的变形应⽤。

统计相同元素出现次数
根据统计的结果将序列回收到原来的序列中

先将数组里面的全部元素映射到count数组中（统计各个元素有多少个，count数组下标是数组元素映射值），再根据count数组映射到arr数组从而实现有序（count数组下标依次增大，所映射的元素也是依次增大）。
在这里插入图片描述
为什么上面说count数组下标是数组元素的映射值，这个映射怎么理解？

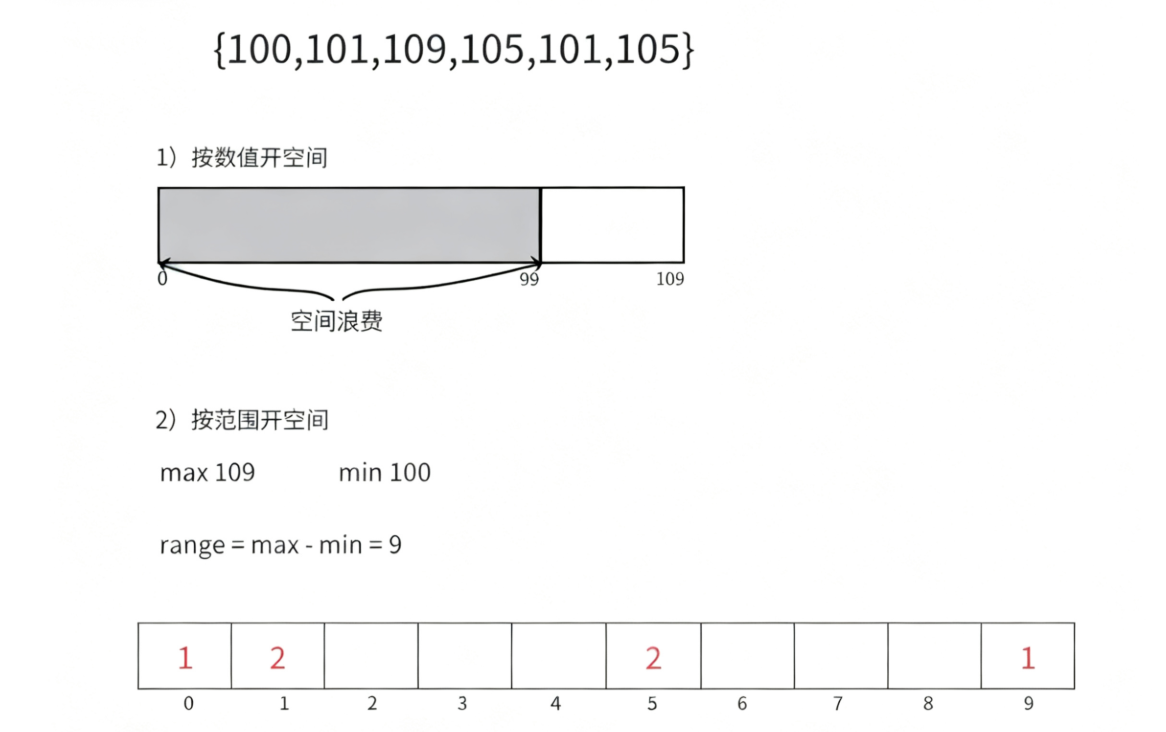
当数组最小值元素过于大时，如果也是按count数组下标就是数组中的元素大小时，这样便会浪费大量的空间，所以我们选择映射，按范围开辟空间，将最小的数组元素映射为count的第一个元素下标0。

2.1 代码实现

#include<stdio.h>
#include<stdlib.h>
void CountSort(int* arr,int n)
{int min = arr[0], max = arr[0];for (int i = 0; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//找到最大值和最小值确定区间int range = max - min + 1;int* count = (int*)calloc(range,sizeof(int));if (count == NULL){perror("realloc failed!");exit(1);}for (int i = 0; i < n; i++){count[arr[i] - min]++;}//再将count映射到arr上去int index = 0;for (int i = 0; i < range; i++){while (count[i]){arr[index++] = i + min;count[i]--;}}free(count);
}
int main()
{int arr[] = {2,4,3,7,5,9,6,8,1};int len = sizeof(arr) / sizeof(arr[0]);CountSort(arr,len);for (int i = 0; i < len; i++){printf("%d ", arr[i]);}return 0;
}