DFS专题（二）洪水填充问题(C++实现，结合lc经典习题讲解)

        上次我们介绍了回溯类的一些经典题目，休息了几天我们继续来围绕着DFS的专题进行介绍。今天我们用一个专题来介绍另一种经典的DFS类题型--洪水填充问题。顾名思义，洪水填充就像把一桶水倒在地图上某个点一样，水会自动向四周蔓延，直到遇到边界为止。一般来讲洪水填充问题都是以二维网格为基础场景的。普通的洪水填充问题是“没有回头路”的，也就是不带回溯操作，路径信息不撤销，但是本文我们也会介绍“带回溯操作”的搜索类问题。在我个人看来，洪水填充问题就是回溯思想的一种“特殊简化版”。今天我也选出了一些在我看来很经典的题目进行介绍。此处声明：我的文章参考了左程云老师的课程和灵茶山艾府等大神的题解，融合我自己的理解进行介绍。
leetcode 130 被围绕的区域

        题设给出了标记“X”和“O”的含义，也分别详细的给出了“连接”，“区域”，“围绕”的概念，这里不再进行赘述，我这里贴出来leetcode的官方示例，供大家理解：

        

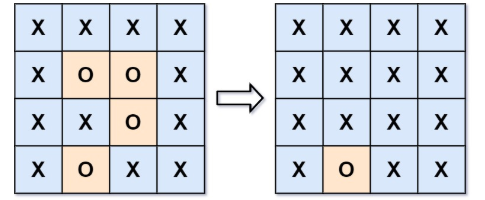
        这道题的中心思想就是被"X"围绕的"O"会被自动感染成“X”。在上面的图例中，由于下方的“O”处于边界，并没有真正意义上的被“X”包围，所以它不会被“感染”。实际上，所有不被包围的“O”，它一定会与边界上的“O”以直接或者间接的方式相连。所以我们现在的任务是从各个边界出发，找出所有与边界“O”直接或间接相连的“O”，并将其标记(假设标记为“F”)。最后遍历整个矩阵，如果发现是“F”，我们将这些“F”还原为“O”。如果发现是“O”说明这些才是被围绕的区域，将其改为“X”即可。示例代码如下：

class Solution {
public:void dfs(vector<vector<char>>& board, int n, int m, int i, int j) {if (i == -1 || i == n || j == -1 || j == m || board[i][j] != 'O') {return;}board[i][j] = 'F'; // 标记为已访问dfs(board, n, m, i + 1, j);dfs(board, n, m, i - 1, j);dfs(board, n, m, i, j + 1);dfs(board, n, m, i, j - 1);}void solve(vector<vector<char>>& board) {int n = board.size();if (n == 0) return; // 空矩阵直接返回int m = board[0].size();// 上下边界for (int j = 0; j < m; j++) {if (board[0][j] == 'O') {dfs(board, n, m, 0, j);}if (board[n - 1][j] == 'O') {dfs(board, n, m, n - 1, j);}}// 左右边界for (int i = 1; i < n - 1; i++) {if (board[i][0] == 'O') {dfs(board, n, m, i, 0);}if (board[i][m - 1] == 'O') {dfs(board, n, m, i, m - 1);}}// 遍历矩阵，修改 'O' 为 'X'，恢复 'F' 为 'O'for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (board[i][j] == 'O') {board[i][j] = 'X';}if (board[i][j] == 'F') {board[i][j] = 'O';}}}}
};

leetcode 827 最大人工岛

        在看下面的介绍之前，请大家一定先准确的理解题意，1所在的位置代表岛屿。这道题其实是岛屿问题的一个拓展问题吧，其前置题目为leetcode 695 岛屿的最大面积，也着实是一道好题。这道题目的关键点在于“最多只能将一格0变成1”。我们其实应该想想，为什么要把0变成1呢？假如两个岛屿中间仅差一格0，那我们把这个0变成1，就类似于“填海造陆”，成功地把两个，或者若干个岛屿连接在了一起。这时候可能会有人想，如果直接遍历水域0，然后进行填充，这时周围的岛屿会连接起来，我们可以直接累加吗？不可以！因为这些“1”可能来自同一个岛屿，我们必须对其进行区分。

        显然我们需要先孤立统计地图上所有现有岛屿的面积，采用洪水填充的感染策略，但是我们需要区分不同岛屿，所以我们需要采用从2开始的自增标记。之后我们的重点就是要找出那个“性价比最高”的0。这个过程没有什么捷径，我们只能在这个矩阵中遍历所有的0进行讨论。以这个0为中心，“吸纳”上下左右四个方向的岛屿(累加逻辑)，之后不断以求最大值的方式进行更新，由此便能得到“最大人工岛”的面积，示例代码如下：

class Solution {
public:void dfs(vector<vector<int>>& grid,int n,int m,int i,int j,int id){if(i<0||i==n||j<0||j==m||grid[i][j]!=1){return;}grid[i][j]=id;dfs(grid,n,m,i-1,j,id);dfs(grid,n,m,i+1,j,id);dfs(grid,n,m,i,j-1,id);dfs(grid,n,m,i,j+1,id);}int largestIsland(vector<vector<int>>& grid) {int n=grid.size();int m=grid[0].size();int id=2;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==1){dfs(grid,n,m,i,j,id++);}}}vector<int> sizes(id);int ans=0;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]>1){ans=max(ans,++sizes[grid[i][j]]);}}}//讨论所有的0变成1，能带来的最大岛屿大小vector<bool> visited(id);int up,down,left,right,merge;for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(grid[i][j]==0){//是否有上下左右，如果有，把编号拿出来up=i>0?grid[i-1][j]:0;down=i+1<n?grid[i+1][j]:0;left=j>0?grid[i][j-1]:0;right=j+1<m>0?grid[i][j+1]:0;//先吸纳上面的岛visited[up]=true;merge=1+sizes[up];if(!visited[down]){merge+=sizes[down];visited[down]=true;}if(!visited[left]){merge+=sizes[left];visited[left]=true;}if(!visited[right]){merge+=sizes[right];visited[right]=true;}ans=max(ans,merge);visited[up]=false;visited[down]=false;visited[left]=false;visited[right]=false;}}}return ans;}
};

leetcode 803 打砖块

        这道题的题意相对而言还是比较难理解的。在这道题目我们需要注意“砖块”是“易碎且有黏性”的。砖块是吊在“天花板”上的，炮弹打到砖块之后，当前砖块会碎掉，而其下黏着的砖块会掉落。也就是说每次打砖块可能会导致连锁坍塌。而这道题目需要我们求的是掉落砖块的数量。我们结合下面画的这张图例进行讲解：

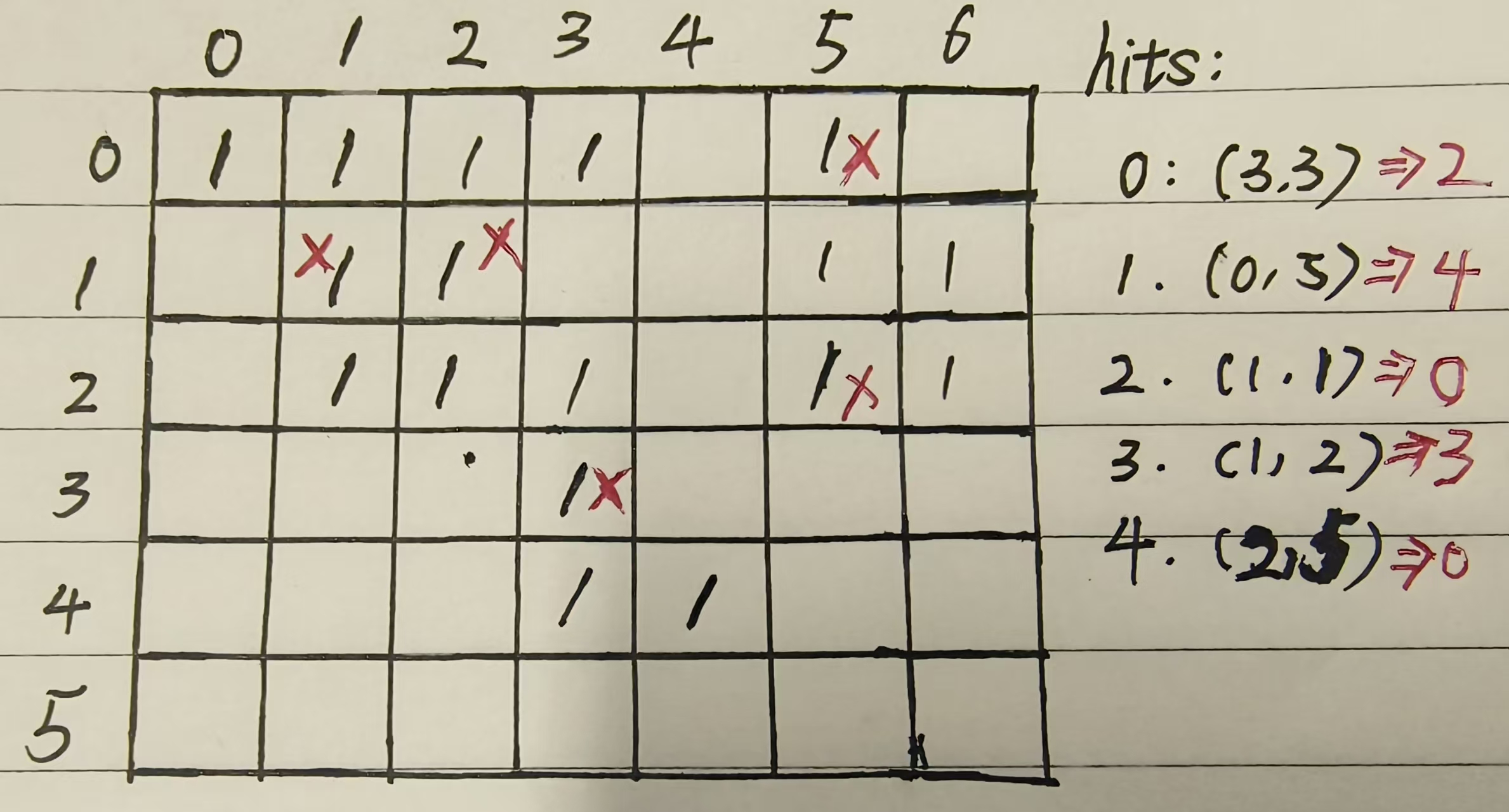
        hit数组代表我们打砖块的位置。假设第一发炮弹打在(3,3)位置，那么(3,3)处位置的砖块会直接碎掉，而(4,3),(4,4)处的砖块因为失去了(3,3)处砖块的黏着，会掉落，所以此时掉落的砖块数为2。第二发炮弹打在(0,5)位置同理，(1,5),(1,6),(2,5),(2,6)四个砖块会被打掉，所以此时掉落的砖块数为4。第三发炮弹打在(1,1)位置，当前砖块碎掉，但是不会有砖块掉落。可能我们很容易想到按照顺序进行模拟即可，但是我们在打完每一发炮弹之后，都需要重新计算连通性并更新状态。假设遇到网格很大或者hit次数很多的极端案例，这个时间复杂度是我们难以容忍的，必然导致超时；而且这道题中蕴含的连锁反应不好处理，我们必须换个角度进行思考。

        既然顺着来发现不太好办，那我们试试倒着做，也许会有意外之喜。我们与其顺序的打掉砖，不如先“假装所有砖块都已被打掉”，然后再从最后一个炮弹开始倒着把砖块加回来。我们选择这种策略的理由是：连通性是只增不减的，实际上我们加回来的砖，要么什么都不变，要么只会让其他的砖更稳定，所以我们每次只需处理增量即可，不需要推翻重来。我们先对这个矩阵进行预处理，把所有被炮弹打中的砖先减1。这样我们就得到了一张打完所有炮弹的状态图。接下来我们从天花板出发进行洪水填充，这些砖经历了所有炮弹都没有掉下来，所以一定是稳定砖。由此稳定砖都会被标记为2。这就是整个过程的“初始稳定”状态。接下来我们逆序遍历hits，把这些砖块打中的炮弹加回去。而且只有与稳定砖相邻的砖块才值得被加回去，这里我们只需要简单判断即可。这种思考方式我们也称为“时间倒流”，值得我们思考与学习，示例代码如下：

class Solution {
public:vector<vector<int>> grid;int n, m;// 从 (i, j) 出发，遇到 "1" 就感染成 "2"，返回新增了几个 "2"int dfs(int i, int j) {if (i < 0 || i == n || j < 0 || j == m || grid[i][j] != 1) {return 0;}grid[i][j] = 2; // Mark as stablereturn 1 + dfs(i + 1, j) + dfs(i, j + 1) + dfs(i - 1, j) + dfs(i, j - 1);}// 检查 (i, j) 是否值得修复bool worth(int i, int j) {return grid[i][j] == 1 && (i == 0 || (i > 0 && grid[i - 1][j] == 2) || (i < n - 1 && grid[i + 1][j] == 2) || (j > 0 && grid[i][j - 1] == 2) || (j < m - 1 && grid[i][j + 1] == 2));}vector<int> hitBricks(vector<vector<int>>& inputGrid, vector<vector<int>>& hits) {grid = inputGrid;n = grid.size();m = grid[0].size();vector<int> ans(hits.size(), 0);if (n == 1) {return ans;}// 预处理：先将所有炮弹命中的砖块标记for (auto &hit : hits) {grid[hit[0]][hit[1]]--;}// 天花板 "洪水填充"，找到所有稳定砖块for (int i = 0; i < m; i++) {dfs(0, i);}// 逆序处理炮弹for (int i = hits.size() - 1, row, col; i >= 0; i--) {row = hits[i][0];col = hits[i][1];grid[row][col]++;if (worth(row, col)) {ans[i] = dfs(row, col) - 1;}}return ans;}
};

leetcode 212 单词搜索II

        我承认这篇文章有点点标题党了哈~不过在我认为，洪水填充是二维网格图DFS的一种非常特殊的情况，不需要进行回溯，所以整个的情况是要简单不少的，那我们就来看看比较一般的情况是怎么回事。我这里给出leetcode官方的示例图来帮助朋友们进行理解：

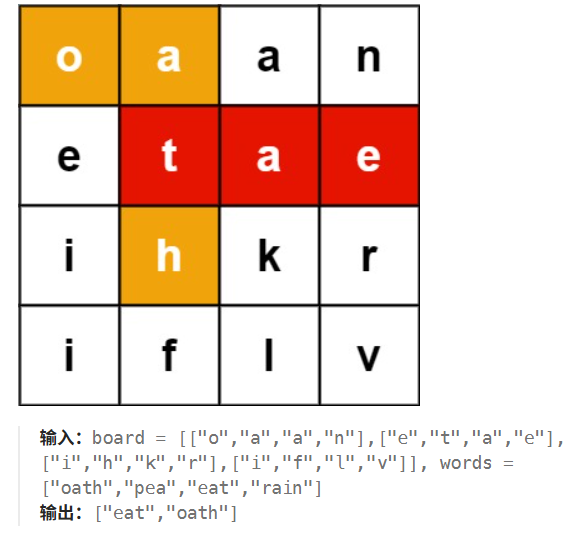
         实际上我们是在一张二维网格图中与字典中的单词进行匹配，匹配成功则将单词返回。根据我们之前的做题经验，我们很容易想到从二维网格的每个格子出发，采用类似洪水填充的方式进行DFS匹配，一旦匹配出的字符串和字典中的单词相同，就返回这个字符串。但是实际上，我们要匹配的不止一个单词，需要去尝试匹配这个字典中所有的单词，如果当前字符没能匹配出来，我们需要进行回溯并恢复现场。但是实际上这么做的时间复杂度是很高的，至少肉眼可见有O(n2*指数)的级别。我们没有必要从每个格子都开始搜索，实际上单词中是存在一种“前后缀”关系的。我们可以以字典为基准构建一棵前缀树。如果走到一个不存在的节点（即没这个前缀），可以立刻停止 DFS。由此我们并非暴力拼字，而是沿着前缀树进行匹配。当前缀树中已经没有下一个节点时，就可以立刻回溯（剪枝）。示例代码如下：

struct TrieNode {string word;TrieNode* children[26] = {nullptr};
};class Solution {
public:vector<string> ans;TrieNode* root;void insert(string word) {TrieNode* node = root;for (char c : word) {int idx = c - 'a';if (!node->children[idx]) node->children[idx] = new TrieNode();node = node->children[idx];}node->word = word; }void dfs(vector<vector<char>>& board, int i, int j, TrieNode* node) {char c = board[i][j];if (c == '#' || node->children[c - 'a'] == nullptr) return;node = node->children[c - 'a'];if (node->word != "") {   ans.push_back(node->word);node->word = ""; }board[i][j] = '#';if (i > 0) dfs(board, i-1, j, node);if (j > 0) dfs(board, i, j-1, node);if (i < board.size()-1) dfs(board, i+1, j, node);if (j < board[0].size()-1) dfs(board, i, j+1, node);board[i][j] = c;}vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {root = new TrieNode();for (auto &w : words) insert(w);for (int i = 0; i < board.size(); i++) {for (int j = 0; j < board[0].size(); j++) {dfs(board, i, j, root);}}return ans;}
};

leetcode 417 太平洋大西洋水流问题

        在看下面的介绍之前，也请朋友们一定深刻思考，理解题意，下面我贴出了leetcode官方的示例供大家参考理解，我们也基于此进行介绍。题目的返回的二维元组表示水流既可流入太平洋，也可流入大西洋的单元格。它只要求从该格子出发，有一条路能去左/上边界，另一条能去右/下边界。角落只是交界，不是必经之地。

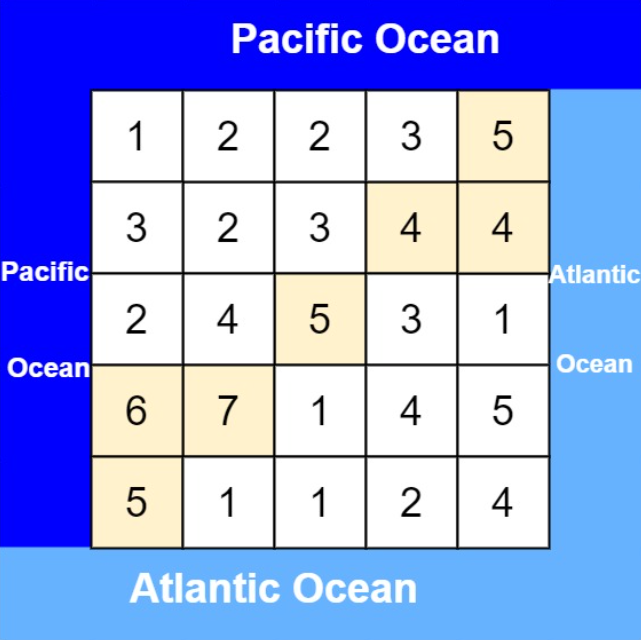
        一开始我其实会想，我从每个格子出发，看它能不能同时流到两个大洋。但问题在于，DFS洪水填充是向外扩充的思想，这道题不完全是这样，因为“水往低处流”，所以其实思考了半天发现正向DFS逻辑是很难说得通的，也很难整理出来用代码实现。我们不妨换个思路，与其让水“流下去”，不如让海洋“反向地”沿着可以流回来的路径“蔓延上来”。也就是说太平洋从左边界、上边界开始“反向灌溉”，大西洋从右边界、下边界开始“反向灌溉”。因为从海洋向陆地反向扩张，只有当陆地比海洋高或相等，才可能形成一条能“往下流”的路径。最后我们取两个区域的交集即可。洪水填充问题一般是属于“同类传播”，而这道题是属于是一种“条件传播”。示例代码如下：

class Solution {
public:void dfs(vector<vector<int>>& heights, vector<vector<bool>>& visited, int i, int j) {visited[i][j] = true;int m = heights.size(), n = heights[0].size();if (i > 0 && !visited[i-1][j] && heights[i-1][j] >= heights[i][j]) {dfs(heights, visited, i-1, j);}if (i < m-1 && !visited[i+1][j] && heights[i+1][j] >= heights[i][j]) {dfs(heights, visited, i+1, j);}if (j > 0 && !visited[i][j-1] && heights[i][j-1] >= heights[i][j]) {dfs(heights, visited, i, j-1);}if (j < n-1 && !visited[i][j+1] && heights[i][j+1] >= heights[i][j]) {dfs(heights, visited, i, j+1);}}vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {int m = heights.size(), n = heights[0].size();vector<vector<bool>> pacific(m, vector<bool>(n, false));vector<vector<bool>> atlantic(m, vector<bool>(n, false));for (int i = 0; i < m; i++) dfs(heights, pacific, i, 0);for (int j = 0; j < n; j++) dfs(heights, pacific, 0, j);for (int i = 0; i < m; i++) dfs(heights, atlantic, i, n-1);for (int j = 0; j < n; j++) dfs(heights, atlantic, m-1, j);vector<vector<int>> result;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (pacific[i][j] && atlantic[i][j])result.push_back({i, j});}}return result;}
};

        今天我们见识了几道经典的洪水填充问题及其变体。从表面上看，洪水填充只是一个在网格中蔓延的 DFS 模板；但深入理解后，你会发现它其实是一种关于“可达性”的思维方式。无论问题的背景是水流、岛屿、还是单词，它们的本质都是：从某个起点出发，沿着规则不断扩散，直到边界或条件终止。当我们掌握了洪水填充，我们不只是学会了写 DFS，而是学会了在复杂系统中找传播规律、控制递归边界、维护访问状态。有不当之处还请大家多多批评指正，我们一起成长！