深度学习（6）激活函数与多类别
在神经网络（Neural Network）中，激活函数（Activation Function） 是一个非常核心的概念。它决定了每个神经元的输出方式，也直接影响模型的非线性表达能力和训练效果。
本篇笔记将从激活函数的选择出发，讲解不同任务下该如何使用激活函数，并说明其背后的原因。
一、激活函数的作用
激活函数的主要功能是为神经网络引入非线性（Non-linearity）。如果没有激活函数，网络的每一层仅仅是线性变换的叠加，最终仍然等价于一个线性模型，这样就无法学习复杂的映射关系。
激活函数常被放在每一层的输出之后，例如：
其中
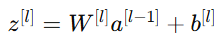
g(⋅) 表示激活函数（如 sigmoid、ReLU、tanh 等）
二、选择激活函数的场景指南
激活函数的选择与任务类型密切相关。下面逐一讲解常见的应用场景。
1. 二分类问题（Binary Classification）
在二分类任务中（例如判断猫/狗、垃圾邮件/正常邮件），输出 y 通常取值为 0 或 1。推荐激活函数：Sigmoid
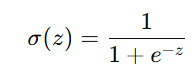
优点：
输出值在 (0,1) 之间，可以直接作为概率解释；
适用于输出层。
示例：
# 二分类输出层
output = tf.keras.layers.Dense(1, activation='sigmoid')
2. 回归问题（Regression）
在回归问题中，输出是连续值，例如预测房价、股票价格等。推荐激活函数：线性激活（Linear Activation）
优点：
不限制输出范围；
能精确预测任意实数值。
示例：
# 回归输出层
output = tf.keras.layers.Dense(1, activation='linear')
3. 输出非负的回归问题
如果预测目标 
，例如预测「放假天数」、「销量」、「温度」等非负值，推荐激活函数：ReLU（Rectified Linear Unit）
优点：
输出自然为非负；
计算速度快；
收敛效果好。
示例：
output = tf.keras.layers.Dense(1, activation='relu')
4. 隐藏层的激活函数选择
在隐藏层（Hidden Layer）中，激活函数的选择通常遵循以下经验：
| 层类型 | 推荐激活函数 | 说明 |
|---|---|---|
| 隐藏层 | ReLU | 收敛快、梯度稳定、不易饱和 |
| 输出层（二分类） | Sigmoid | 输出为概率 |
| 输出层（回归） | Linear | 输出为实数 |
| 输出层（非负回归） | ReLU | 输出为非负数 |
| 输出层（多分类） | Softmax | 输出为多类别概率 |
三、ReLU 与 Sigmoid 的比较
| 对比项 | ReLU | Sigmoid |
|---|---|---|
| 计算速度 | 快，仅需取 max(0, z) | 慢，需要指数运算 |
| 梯度下降 | 梯度更稳定 | 容易梯度消失 |
| 非线性区间 | 仅 z > 0 时激活 | 全区间平滑激活 |
| 常见用途 | 隐藏层 | 输出层（二分类） |
总结：
ReLU 更适合隐藏层；
Sigmoid 适合输出层；
如果网络层数较深，使用 Sigmoid 可能出现梯度消失问题。
四、多类别分类问题（Multi-class Classification）
对于类别数大于 2 的分类任务，例如识别手写数字（0–9）、动物种类（猫、狗、马等），推荐激活函数：Softmax
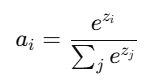
特点：
将输出转化为概率分布；
各类别概率之和为 1；
与交叉熵损失函数（Cross-Entropy Loss）配合使用效果最好。
示例：
# 多分类输出层
output = tf.keras.layers.Dense(num_classes, activation='softmax')
五、总结
| 任务类型 | 输出层激活函数 | 隐藏层激活函数 |
|---|---|---|
| 二分类 | Sigmoid | ReLU |
| 多分类 | Softmax | ReLU |
| 回归（实数） | Linear | ReLU |
| 回归（非负） | ReLU | ReLU |
关键要点：
隐藏层一般使用 ReLU；
输出层根据任务类型灵活选择；
激活函数让神经网络能学习复杂非线性映射；
选择合适的激活函数是训练成功的关键。