Java数据结构：Stack(栈)Queue(队列)

一、栈（Stack）

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出的原则。

入栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据在栈顶。

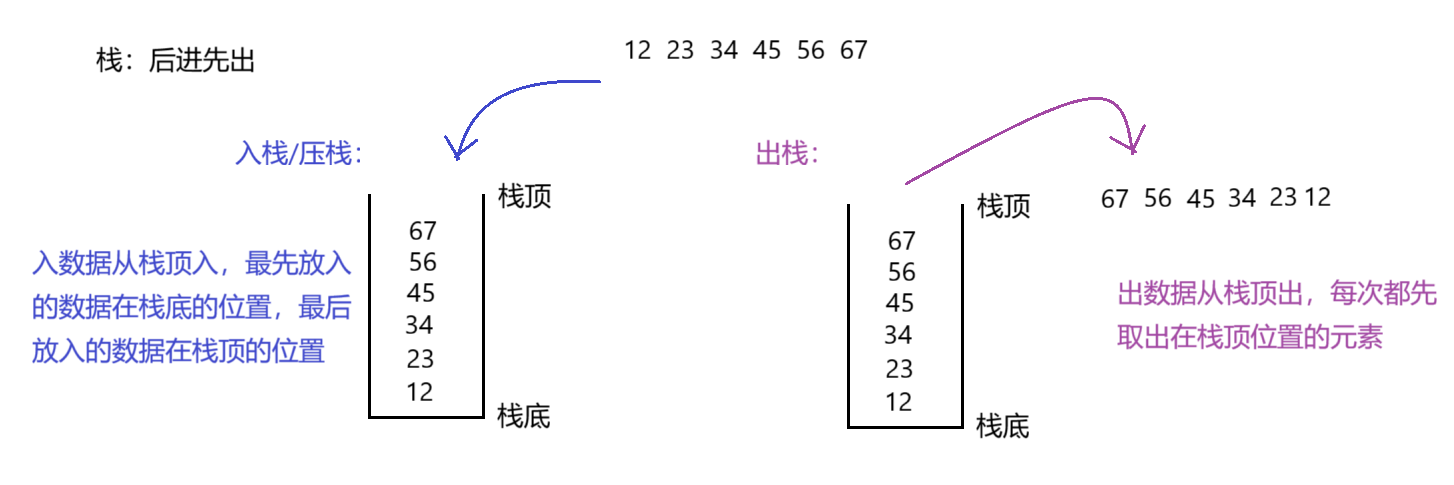
就像在叠一次性杯时，第一个叠的最终是在最底部，最后一个叠的在最上面；而在拿一次性杯子的时候，都会从最上部拿一个杯子。

栈的使用

我们先看看Stack栈的源码：它是一个泛型类并继承于Vector类，那么它除了可以使用自身的方法外，也可以使用Vector类中的方法。

Stack类中的方法：

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

我们可以使用Stack泛型类进一步验证入栈和出栈的过程：

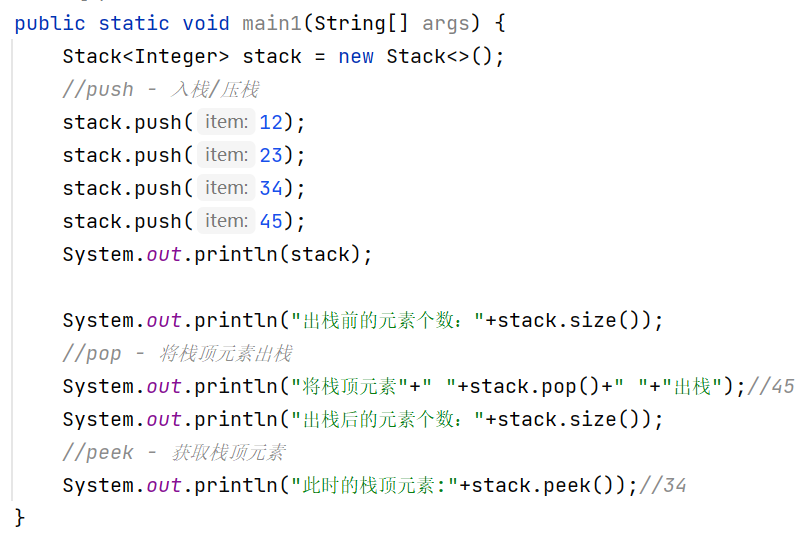
输出结果：

栈的模拟实现

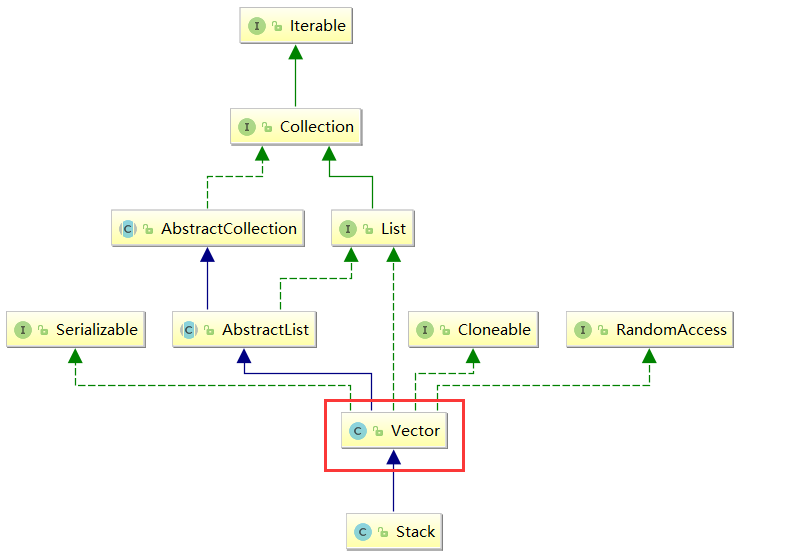
从上图可以看出，Stack继承了Vector，而Vector和ArrayList类似，都是动态的顺序表，不同的是Vector是线程安全的。因此，我们在模拟实现Stack的时候，采用顺序表的思路来实现。

思路：首先创建一个MyStack类，表示模拟实现Stack的一个类，这个类中包含Stack中的方法，再写一个IStack接口，让MyStack类实现这个接口，然后实现该接口中的抽象方法。

1.IStack接口的完整框架

在这个接口中，有Stack类中的方法，例如push方法等，MyStack类会继承该接口，然后重写这些方法。

public interface IStack {//将val入栈，并返回valint push(int val);//将栈顶元素出栈并返回int pop();//判断栈是否为空boolean empty();//获取栈顶元素int peek();//获取栈中有效元素的个数int size();
}

2.MyStack类的完整框架

以顺序表的思路实现该类，我们知道顺序表一般情况下是采用数组存储的，因此，我们需要在该类中定义一个数组（这里以int类型为例），用来存放栈中的元素，另外，定义一个变量usedSize，表示栈中有效元素的个数；然后构造一个无参构造方法，用来对数组进行初始化。

不要忘记让该类实现IStack接口，然后实现抽象方法。

public class MyStack implements IStack {public int[] array;public int usedSize;public MyStack() {this.array = new int[10];}//重写接口中的抽象方法public int push(int val) {}……………………
}

现在，类和接口的整体框架已经说明完毕，现在，详细说明在MyStack类中如何重写抽象方法。

[1] push() 入栈

该方法的作用是向栈中添加元素（从栈顶入栈），并返回添加的元素val。

不过，在入栈之前，要先判断栈是否已经满了，如果满了，返回true，对栈进行扩容，然后再入栈；否则，返回false，直接将元素入栈，写一个方法isFull()来实现判满操作(如果有效元素个数usedSize的值等于array数组的长度，表示栈已经满了)。

扩容：使用Arrays类中的copyOf()方法来进行扩容操作，该方法的作用：用于复制数组并指定新数组长度。利用copyOf方法复制原数组并指定这个新数组的长度是原数组长度的2倍（以2倍数增长），最后将这个新数组赋值给原数组array，这样就表示增容成功。

(1.1) isFull() 判断栈是否已满

public boolean isFull() {return usedSize == array.length; //如果相等，表示满了，返回true，否则返回false
}

(1.2) push()

public int push(int val) {if(isFull()) {//满了，进行扩容this.array = Arrays.copyOf(this.array,2*this.array.length); }array[usedSize++] = val;//将val入栈，有效元素usedSize个数增加return val;
}

[2] empty() 判断栈是否为空

如果有效元素个数usedSize的值等于0，表示栈为空，返回true，否则返回false。

public boolean empty() {return usedSize == 0;
}

[3] pop() 出栈

该方法的作用是将栈顶元素出栈（从栈顶出栈），并返回出栈的栈顶元素。

注意：每次将栈顶元素出栈后，栈中的有效元素个数也会相应的减少，也就是说，原来的栈顶元素出栈后，该元素的前一个元素就会变成新的栈顶元素。

总结为一句话就是：将栈顶元素出栈并返回，会删除栈顶元素。

在出栈之前，先对栈判空，这里写一个EmptyStackException-空栈异常类，如果栈为空，抛出异常，不能进行出栈操作。

(3.1) EmptyStackException异常类

public class EmptyStackException extends RunTimeException {public EmptyStackException() {super();} public EmptyStackException(String message) {super(message);}
}

(3.2) pop()

用变量val来接受栈顶元素（因为要返回出栈的元素，所以在删除之前保存一下），然后usedSize直接--，即表示已经删除了该栈顶元素。

例如：现在栈中有1，2，3，4 这4个元素，它们的下标分别是0~3，此时要删除栈顶元素4，即下标为3的位置的元素，先使用val接收后，usedSize--，表示删除4后，有效元素个数为3个，这3个元素对应的下标分别为0~2；下次想要增加一个5，那么usedSize++，那么有效元素个数又变回4，对应的下标为0~3，那么5就直接覆盖了4，成为新的下标为3位置上的元素。

public int pop() {if(empty()) {//如果栈为空，无需出栈操作，抛出异常throw new EmptyStackException("空栈");}int val = array[usedSize-1];usedSize--;return val;
}

[4] peek() 获取栈顶元素

该方法和pop()方法的做法一模一样，但是peek()方法只是获取栈顶元素，即只是想要知道栈顶元素是什么而已，不会删除栈顶元素。

一句话总结就是：获取栈顶元素，但是不删除栈顶元素。

public int peek() {if(empty()) {throw new EmtpyStackException("空栈");}return array[usedSize-1];//返回栈顶元素
}

[5] size() 获取栈中有效元素个数

栈的有效元素个数就是usedSize的值，那么直接返回usedSize即可。

public int size() {return this.usedSize;
}

到这里，Stack的模拟实现圆满完成。

问题1：我们模拟实现的栈采用的是顺序表的思路，那么，使用单链表是否可以实现栈？

—— 采用顺序表实现的栈，叫做顺序栈，入栈和出栈的时间复杂度都是O(1)。那么采用单链表：

如果采用尾插/删法（单链表的尾节点位置就类似于栈顶，入栈或者出栈的那一固定端），那么入栈的时间复杂度为O(n)，因为需要遍历链表找到尾节点，然后再进行入栈操作，而如果有last引用标记尾节点，那么入栈的时间复杂度为O(1)，但是，出栈操作就一定是O(n)，因为又得重新遍历链表找到尾节点，然后再进行出栈操作。

如果采用头插/删法（单链表的头节点位置就类似于栈顶，入栈或者出栈的那一固定端），那么入栈的时间复杂度为O(1)，同时出栈的时间复杂度也为O(1)。因此，如果采用单链表实现栈，那么可以采用头插法的形式入栈和采用头删法的形式出栈。

问题2：使用双链表是否可以实现栈？

—— 采用双向链表实现栈是完全可以的，不管是采用头插法还是尾插法，入栈和出栈的时间复杂度都是O(1)。

采用单链表/双链表实现的栈，叫做链式栈。

我们可以查看LinkedList类中的方法，发现它是包含push、pop、peek等方法的：

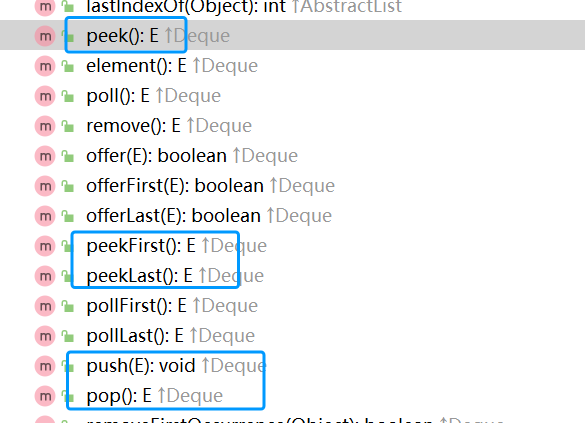
示例：

栈的应用

1.改变元素的序列

• （1）若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）

        A: 1,4,3,2           B: 2,3,4,1           C: 3,1,4,2           D: 3,4,2,1

分析：

A选项✔，按照 1,4,3,2 出栈的过程：当1入栈后，又出栈了，此时出栈序列的第一个元素就是1，现在栈又变回空的，接着继续按照进栈的顺序进栈，此时栈内的元素是2，3，4，2在栈底的位置，4在栈顶的位置；最后将栈中的所有元素出栈（是从栈顶出栈的），那么此时出栈序列的顺序是 4，3，2，最终的出栈序列为 1，4，3，2。

B选项✔，按照 2,3,4,1 出栈的过程：当1入栈后，就是2入栈，而2在入栈后，又出栈了，因此，出栈的序列的第一个元素是2，此后的3，4也重复了2的操作后，出栈序列的顺序为2，3，4，最后再将最开始入栈的1也进行出栈，因此，最终的出栈序列的顺序为 2，3，4，1。

C选项❌，按照 3,1,4,2 出栈是不可能的：想要让3是出栈序列的第一个元素，那么要让1，2入栈后，才能让3入栈又出栈，那么1就不可能在3之后出栈，它们之间还隔了2。

D选项✔，按照 3,4,2,1 出栈的过程：先让1，2入栈后，3入栈后又出栈，然后4再入栈，此时栈中的元素序列为1，2，4，再将它们出栈，最终出栈序列为 3，4，2，1。

• （2）一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ ）

分析：按照题目顺序依次入栈，然后依次出栈，那么元素出栈的顺序就是：E、D、C、B、A、5、4、3、2、1。

2.将递归转化为循环

比如：逆序打印链表

• 递归方式

void printList(Node head) {if(head != null) {printList(head.next);System.out.print(head.val+" ");}
}

• 循环方式——Stack实现

还是写一个printList方法，首先对链表进行判空，然后遍历链表，使用push()方法，将链表中的节点全部保存到栈中，全部入栈之后，此时的栈不为空，使用pop()方法，将栈中的元素出栈，此时的顺序与入栈的顺序刚好相反，即为逆序。

void printList(Node head) {if(head == null) {return;}Stack<Node> stack = new Stack<>();//将链表中的节点保存到栈中Node cur = head;while(cur != null) {stack.push(cur);cur = cur.next;}//将栈中的元素出栈while(!stack.empty()) {System.out.print(stack.pop().val+" ");}
}

栈、虚拟机栈和栈帧的区别

可以用一个简单的比喻来开始：

栈：就像一个书立或书堆，它决定了书只能从顶部放入或取出（先进后出）。

虚拟机栈：就像是分配给某个人的一个专属书堆。每个人（线程）都有自己的书堆，互不干扰。

栈帧：就是书堆里的每一本书。每本书代表一个任务（方法），书里的页记录了做这个任务需要的具体信息（局部变量、操作数等）。

-----------------------------------------------------------------------------------------------------------------------------

1.栈
这是一个通用的数据结构概念，与编程语言和硬件无关

核心特性：后进先出。

操作：只有两个基本操作：

入栈/压栈：将元素放入栈顶。

出栈/弹栈：从栈顶取出元素。

类比：就像一摞盘子，你总是把新盘子放在最上面（压栈），也总是从最上面拿走盘子（弹栈）。

2.虚拟机栈
这是一个与程序运行相关的内存区域概念，通常特指在Java虚拟机这样的托管环境中。

是什么：它是JVM为每个线程单独创建的一块私有内存区域。

生命周期：与线程相同。线程启动时创建，线程结束时销毁。

作用：用于存储方法调用时的栈帧（即它内部存储着一个一个的栈帧）。它描述了Java方法执行的内存模型：每个方法从调用到执行完成的过程，就对应着一个栈帧在虚拟机栈中从入栈到出栈的过程。

3. 栈帧
这是虚拟机栈的基本组成单位，是方法级别的。

是什么：是用于支持虚拟机进行方法调用和方法执行的数据结构。

生命周期：与方法调用相同。方法被调用时创建栈帧并入栈，方法执行结束时（无论是正常返回还是异常）栈帧出栈。

内部结构：一个栈帧通常包含以下几个部分：

局部变量表：一个数字数组，用于存储方法参数和方法内部定义的局部变量。

操作数栈：一个后进先出的栈，用于执行字节码指令。方法执行过程中的计算、参数传递等操作都在这里进行。

动态链接：指向运行时常量池中该栈帧所属方法的引用。这是为了支持方法调用过程中的动态绑定（多态）。

方法返回地址：方法正常退出或异常退出时，程序计数器应该返回的位置，以便调用者方法能继续执行。

一些附加信息：虚拟机实现可能会添加一些额外信息，如对调试、性能收集的支持等信息。

二、队列（Queue）

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的原则。

入队列：进行插入操作的一端称为队尾（Tail/Rear）。

出队列：进行删除操作的一端称为队头 （Head/Front）。

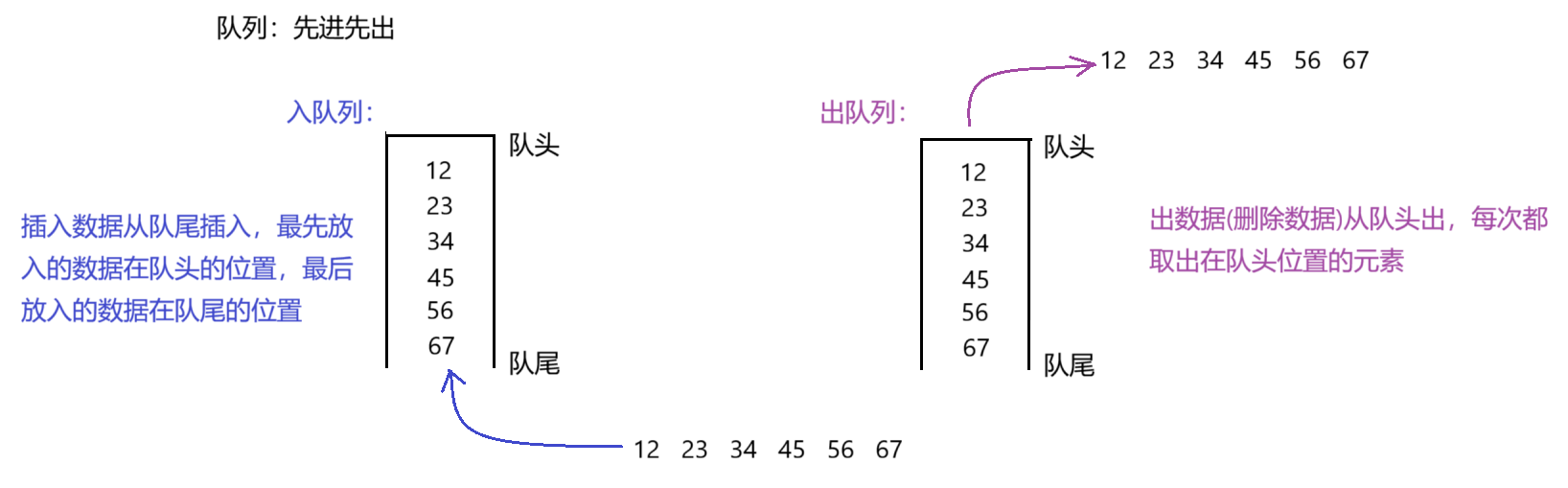
就像人在排队结账一样，每次要排队时都是从队尾的位置开始排进队伍里，结账时是排在队头的人开始的。

比较：队列是遵循先进先出的原则，而栈是遵循后进先出的原则；栈是只能从固定的一端插入和删除数据，即在栈顶进行出栈和入栈，而队列是只允许在一端插入数据，在另一端删除数据，即在队尾入队列，在队头出队列，两头分工明确。

队列的使用

在Java中，Queue是个接口，底层是通过链表实现的。

看Queue接口的源码，它继承与Collection接口，那么它除了可以使用自身的方法外，还可以使用Collection类中的方法，如size()、isEmpty()等方法。

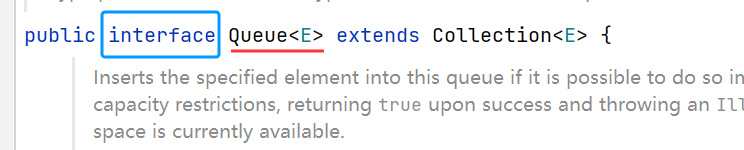
Queue中的方法：

方法	功能
boolean offer(E e)	入队列
E poll()	出队列
E peek()	获取队头元素
int size()	获取队列中有效元素个数
boolean isEmpty()	检测队列是否为空

在Queue接口中，还有add()、remove()、element()方法，这些的功能分别和offer()、poll()、peek()一样，但是我们通常使用的是上述表格上的方法。

注意：如果想要使用Queue接口，即Queue在实例化时，可以实例化LinkedList的对象，因为LinkedList实现了Queue接口。

LinkedList实现了 Deque 接口 ，而 Deque 接口又继承扩展了 Queue 接口：

如下图，LinkedList类中的一些方法：

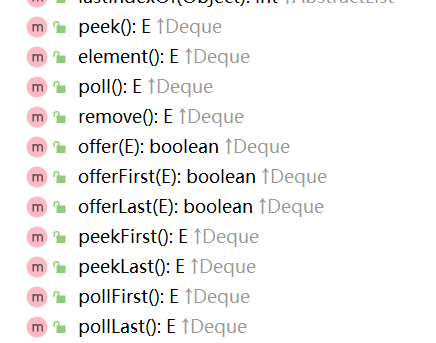
我们可以使用Queue接口进一步验证入队列和出队列的过程：

输出结果：

队列的模拟实现

队列中既然可以存储元素，那底层肯定要有能够保存元素的空间，通过前面线性表的学习了解到常见的空间类型有 两种：顺序结构 和 链式结构。

思考：队列的实现使用顺序结构还是链式结构好？

首先我们先使用链式结构来实现队列，这又分为两种：单链表实现和双链表实现。

• 单链表：如果使用单链表实现队列，那么可以先遍历链表，使用last引用对链表的尾节点进行标记，然后入队列采用尾插法，而出队列则采用头删法（删除头节点）。注意：就算有尾节点的标记，也不能将入队列和出队列的方式倒过来，即采用头插法入队，尾删法出队，因为这样的话，删除还需要找到最后一个节点的前一个节点（需要实时更新尾节点）。
• 双链表：如果使用双链表实现队列，那么采用 尾插法入队、头删法出队 或者 头插法入队、尾删法出队 都可以。出队和入队的时间复杂度都为O(1)。

我们使用双向链表来模拟实现队列，思路：创建一个MyQueue类，表示模拟实现Queue接口的一个类，在这个类中，模拟实现Queue中的方法。

MyQueue类完整框架

public class MyQueue {static class ListNode {public int val;public ListNode prev;public ListNode next;public ListNode(int val) {this.val = val;}}public ListNode first;//队头public ListNOde last;//队尾public int usedSize;//记录队列中有效元素个数//Queue接口中方法的实现public boolean isEmpty() {}//…………………………
}

接下来详细说明MyQueue类中Queue中方法的实现方式。

[1] isEmpty() 检测队列是否为空

如果队列的有效元素个数usedSize等于0，或者它的头节点/队头等于null，那么就代表队列为空。

public boolean isEmpty() {return usedSize == 0;//return first == null;
}

[2] offer() 在队尾入队列

isEmpty() 检测队列是否为空，如果为空，那么就将要入对的 node新节点的val值作为队列的第一个数据；如果不为空，就往队列的尾部添加数据。添加完成，uesdSize++，返回true。

public boolean offer(int val) {ListNode node = new ListNode(val);if(isEmpty()) {first = last = node;}else {last.next = node;node.prev = last;last = last.next;}usedSize++;return true;
}

[3] poll() 在队头出队列

如果队列为空，则返回-1（这里不需要像栈等用异常类进行判空，因为源码中的poll也没有）；如果不为空，则删除队列中的队头位置数据：first往后走，在删除前先保存一下队头节点的数据，如果这个新的first不是空的话，也就是队列中不是只有一个节点的情况，则需要将first的prev引用改成指向null，然后usedSize--，返回原队头节点的数据。

public int poll() {if(isEmpty()) {return -1;}int val = first.val;first = first.next;if(first != null) { //如果此时的新的队头节点不为空，即表示队列中不是只有一个元素first.prev = null;}usedSize--;return val;
}

[4] peek() 获取队头元素

如果队列为空，则返回-1；如果不为空，则直接返回队头元素。

public int peek() {if(isEmpty()) {return -1;}return first.val;
}

[5] size() 获取队列有效元素个数

直接返回usedSize即可。

public int size() {return usedSize;
}

到这里，就完成了队列的模拟实现。

在使用或者实现队列的过程中，我们一直使用的是链式结构，接下来，尝试使用顺序结构实现，即采用数组如何实现队列？

如下图，定义一个数组，使用变量front、rear来分别记录数组头和尾的位置，往数组中添加数据(入队列)后，在将数组中的一些数据出队列，此时的front位置跟着更新，再次添加数据，直到数组空间满，但是数组前面出队列后留出来的空间并没有用到：

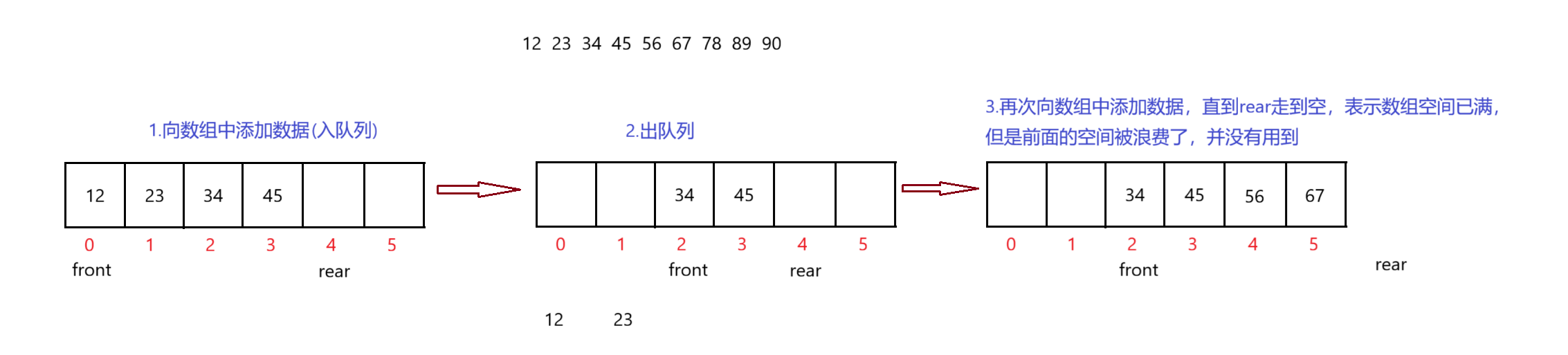
那么，如何让数组能够识别这些空余的空间添加数据？

—— 答案就是将这个数组围成一个环/圆圈，即队头和队尾连接起来形成一个环形队列，这样的队列叫做循环队列。

循环队列

环形队列通常使用数组实现。

向循环队列中存放数据，

问题1：rear 或者 front 下标从 7 位置到 0 位置怎么做到?

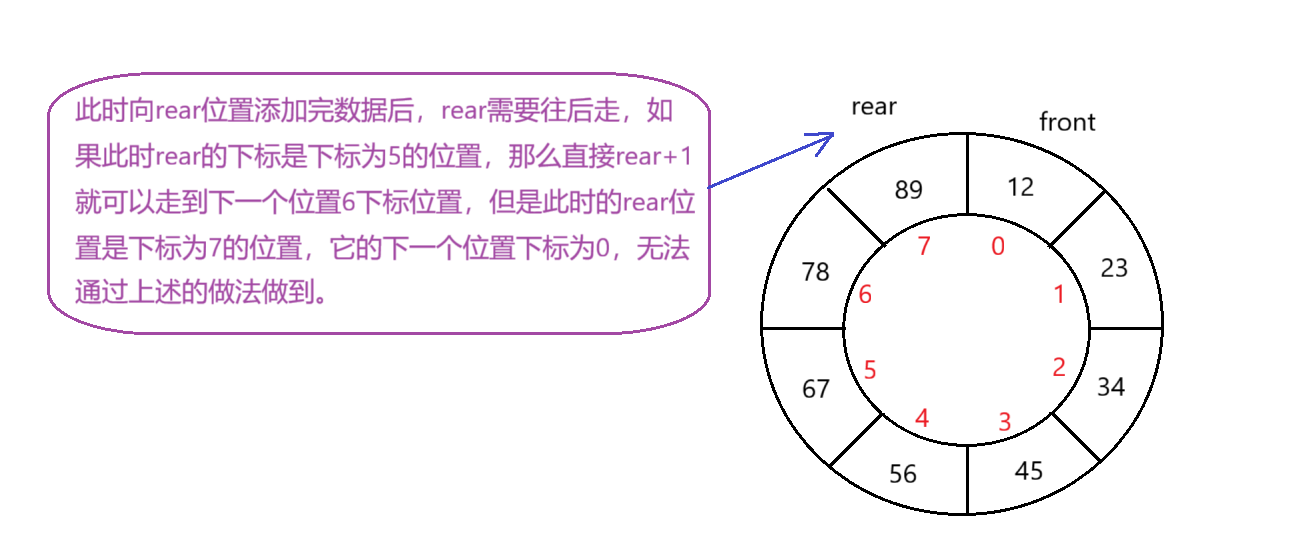
解决方法：通过公式  (rear+1)%array.length 做到，示例，此时rear是下标为5的位置，那么(5+1)%8=6，走到下一个位置下标为6的位置，如果rear是下标为7的位置，那么(7+1)%8=0，就可以做到从下标7走到下标0位置。

问题2：如何判断空和满？（空和满的情况front和rear都在同一个位置）

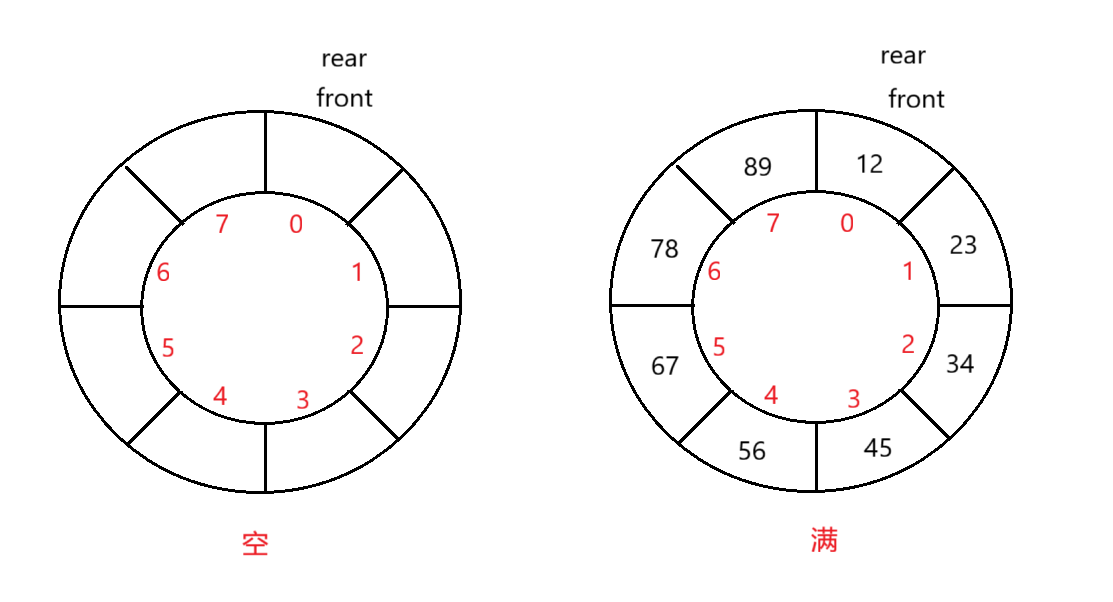
• 循环队列为空：只要front和rear相遇，即它们在相同位置的话(只要位置相同就代表空，无论它们在队列的哪一个下标位置)，就表示空。
• 循环队列满，有三种表示方法：

1.使用一个标志位 size

• 这种方法通过维护一个额外的变量来记录当前队列中的元素个数。
• 核心思想：用一个变量 size 来记录队列的实时长度。
• 判断条件：
• 队列空：size == 0
• 队列满：size == capacity
• 队列长度：直接返回 size 即可。
• 入队操作：在 rear 移动后，执行 size++。
• 出队操作：在 front 移动后，执行 size--。
• 优点：逻辑非常直白，易于理解。不浪费存储空间。
• 缺点：需要维护一个额外的变量，每次入队和出队操作都需要更新它。

2.使用一个标志位 tag

• 这种方法通过一个布尔标志位来记录最后一次操作的类型，以此来判断状态。
• 核心思想：用一个布尔变量 tag。
• 当执行一次 入队 操作时，我们将 tag 设置为  true，表示最后一次操作是“入队”。
• 当执行一次 出队 操作时，我们将 tag 设置为 false，表示最后一次操作是“出队”。
• 判断条件：
• 队列空：(front == rear) && (tag == false)
• （指针重合，且最后一次操作是出队，那肯定是把最后一个元素也拿走了，所以为空）
• 队列满：(front == rear) && (tag == true)
• （指针重合，且最后一次操作是入队，那肯定是因为放入一个元素导致 rear 追上了 front，所以为满）
• 优点：不浪费存储空间。
• 缺点：逻辑上比较复杂一些，需要同时判断指针和标志位。

3.浪费一个空间/保留一个位置

• 这是最经典和直观的方法。
• 核心思想：我们故意不使用数组中的最后一个位置。当 rear 的下一个位置是 front 时，我们就认为队列已满。
• 判断条件：
• 队列空：front == rear
• 队列满：(rear + 1) % capacity == front
• 队列长度：(rear - front + capacity) % capacity
• 示例：假设队列容量 capacity 为 5（即数组长度为 5），那么实际只能存储 4 个元素。
• 初始时 front = rear = 0，队列为空。
• 当插入 4 个元素后，rear 指向第 4 个位置（索引3）。此时 (3 + 1) % 5 = 4，不等于 front (0)，所以还能插入一个元素。
• 插入第 5 个（实际能存的第 4 个）元素后，rear 移动到 4。此时 (4 + 1) % 5 = 0，等于 front (0)，判定为队列已满。
• 优点：逻辑清晰，实现简单，效率高。
• 缺点：浪费了一个数组单元的存储空间。

我们采取第3种做法来表示满的情况。

明白了循环队列的思路之后，我们来设计实现一个循环队列。

设计循环队列

循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间，但是使用循环队列，我们能使用这些空间去存储新的值。
该类中支持以下的操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k 。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull(): 检查循环队列是否已满。

MyCircularQueue类 - 实现循环队列

public class MyCircularQueue {public int[] array;//定义数组存放数据public int front;//标记循环队列队头public int rear;//标记循环队列队尾//构造方法，初始化数组的长度public MyCircularQueue(int k) {array = new int[k+1];//是k+1的原因:在判满的时候，采取浪费一个空间的做法，那么要设置的队列长度是3的话，需要设置长度为4，确保有一个空间可浪费又不会占用要存放的数据个数}}

接下来解说该类中的方法如何实现。

[1] isFull() 判断循环队列是否已满

判满采取 浪费一个空间/保留一个位置 的做法 ，那么满的情况就是——如果rear的下一个位置等于front（ (rear+1)%array.length ），就说明已经满了。

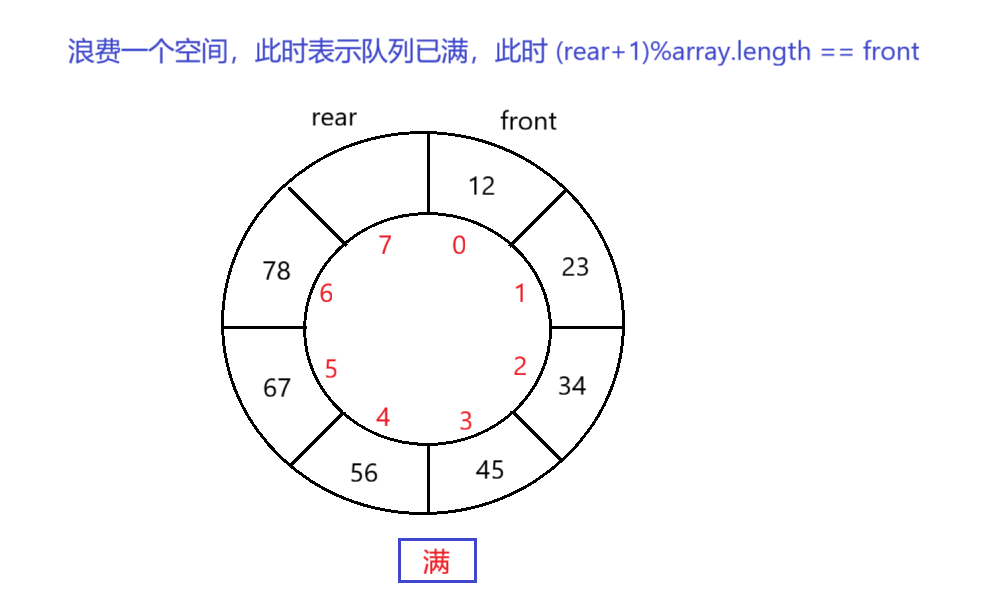
public boolean isFull() {return (rear+1)%array.length == front;
}

[2] isEmpty() 判断循环队列是否为空

如果rear 和 front 位置相同，则代表队列为空(只要位置相同就代表空，无论它们在队列的哪一个下标位置)。

public boolean isEmpty() {return rear == front;
}

[3] enQueue() 入队列

如果队列已满，则返回false；否则，向队尾插入数据，插入完成之后rear往后走（往后走的方式依然使用公式法），然后返回true。

public boolean enQueue(int value) {if(isFull()) {return false;}array[rear] = value;rear = (rear+1)%array.lenght;//rear往后走return true;
}

[4] deQueue() 出队列

如果队列为空，则返回false；否则，从队头删除数据，即front往后走，然后返回true。

无需担心原来front位置上的元素没有真正删除，如果后面再进行入队列操作，而且刚好要插入的位置是原front位置，那它原来存放的数据最终会被覆盖掉。

public boolean deQueue() {if(isEmpty()) {return false;}front = (front+1)%array.length;return true;
}

[5] Front() 获取队头元素

public int Front() {if(isEmpty()) {return -1;}return array[front];
}

[6] Rear() 获取队尾元素

我们知道，尾元素是用 array[rear-1]  （队列走到最后的时候，是在浪费的那个空间的位置上，那么它实际的最后一个元素就是 rear-1 ），但是，这里有一个特殊的情况，如果尾元素的下标是0位置时，0-1就变成了-1，而下标是不允许负数的，因此，需要单独处理当尾元素在0下标位置时的情况：采用三目操作符来解决——如果rear==0，则返回队列长度-1的位置，如果不等于0，则直接减1即可。

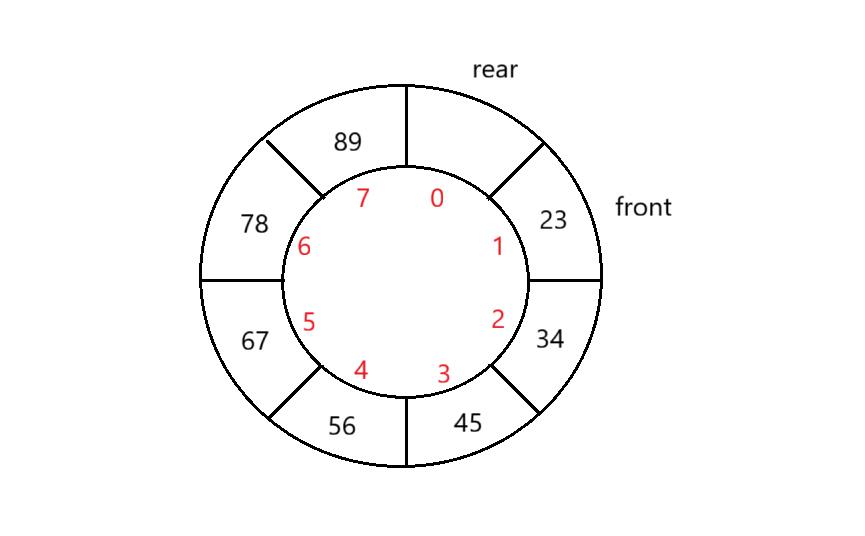
public int Rear() {if(isEmpty()) {return -1;}int index = (rear == 0) ? array.length-1 : rear-1;return array[index];
}

以上，就是循环队列的全部内容。

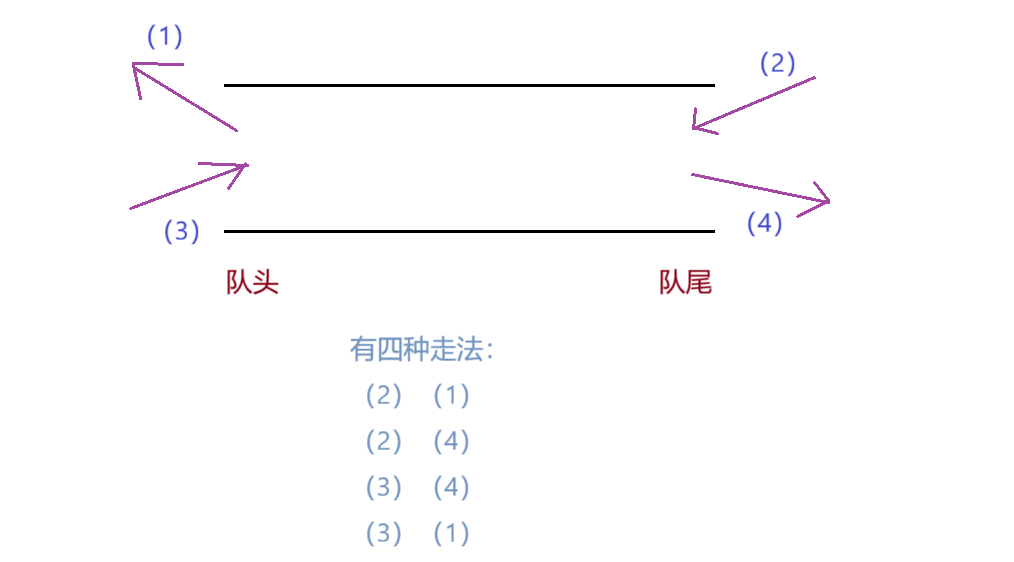
三、双端队列（Deque）

双端队列（deque）是指允许两端都可以进行入队和出队操作的队列，deque 是 “double ended queue” 的简称。 那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。

也就是说，双端队列Deque可以被当作队列和栈来使用。甚至是顺序表、链表使用（Deque中的方法支持）。

看Deque的源码，它是一个接口，继承于Queue接口：

那么，实现Deque，可以通过实例化LinkedLIst的对象实现

Deque<Integer> queue = new LinkedList<>();//双端队列的链式实现

认识另一个双端队列 ArrayDeque，它实现了 Deque 接口，是一个基于数组(循环数组)的双端队列

• ArrayDeque作为双端队列使用：ArrayDeque类也可以实现Deque接口，是双端队列的线性实现：

ArrayDeque<Integer> deque = new ArrayDeque<>();//双端队列的线性实现

• ArrayDeque作为队列使用：Queue除了通过LinkedLIst实现，还可以通过ArrayDeque实现：

ArrayDeque<Integer> queue = new ArrayDeque<>();

• ArrayDeque作为栈使用：可以代替Stack类实现栈，由于 Stack 基于 Vector，性能较差，ArrayDeque 的 push() 和 pop() 方法更适合实现栈：

ArrayDeque<Integer> stack = new ArrayDeque<>();