当前位置：首页 > news >正文

《深入浅出统计学》学习笔记（一）

news 2025/10/28 11:59:50

前言

这篇博客是我在学习《深入浅出统计学》这本书时整理的个人笔记。《深入浅出统计学》作为一本经典的统计学入门书籍，内容由浅入深、案例丰富，全书共 15 章。考虑到知识点的连贯性和阅读体验，我计划将整本书的学习笔记分为 3 篇在 CSDN 上分享，每篇聚焦 5 个章节的内容，本篇便是系列笔记的第一篇，涵盖书中的第 1 章到第 5 章。

在整理笔记的过程中，我会结合书中的核心内容，提炼重点概念、公式推导以及典型例题。为了更直观地呈现书本中的关键图表、例题解析和知识点框架，笔记里穿插了部分书本内容的截图，这些截图将与我的文字解读相互补充，帮助大家更好地理解统计学的基础原理。

由于是个人学习笔记，内容可能会带有一定的个人理解视角，若存在表述不够准确或遗漏的地方，欢迎大家在评论区留言指正。
注意：起初笔记是写在飞书上，现在是转化分享到csdn里，因此部分地方格式显示不全或看着不美观（如公式、图片等）

一、信息图形化

1.频数、百分比

指标	定义	例子
频数	某类别数据的绝对出现次数，是统计的原始结果	得 90 分的学生有 10 人
百分比	某类别数据的相对占比，是频数的标准化结果计算公式：百分比 =（某类别频数 ÷ 总频数）× 100%	得 90 分的学生占 28.57%

两者缺一的局限性

① 只有频数，缺少百分比：缺失 “相对视角”，无法判断重要性

例子：某老师公布月考成绩频数：90-100 分 8 人、80-89 分 15 人、70-79 分 12 人

思考：若不说明班级总人数（总频数），“8 人得高分” 的意义无法判断 —— 若总人数 35 人，高分占比 22.86%（属优秀）；若总人数 200 人，高分占比仅 4%（属平庸）

② 只有百分比，缺少频数：缺失 “绝对规模”，无法落地应用

例子：班主任反馈：喜欢篮球 20%、喜欢足球 15%、喜欢羽毛球 30%

思考：若班级共 20 人，喜欢篮球仅 4 人（难以组队）；若班级共 100 人，喜欢篮球 20 人（有充足活动伙伴）

统计指标的价值在于 “还原数据真相”：
频数提供 “具体数量”，锚定数据的绝对规模
百分比提供 “比例视角”，揭示数据的相对重要性
两者结合，才能全面、准确地解读数据意义！

2.定性数据、定量数据

类型	定义	关键特征	示例
定性数据	又称 “类别数据”，用于描述事物的性质、特征或类别，数据值不具备数字的量化意义	无大小、顺序之分，仅体现类别属性	商品颜色（“红色”“黑色”“白色”）
定量数据	又称 “数字值数据”，以数值形式呈现，既涉及计量/计数，又具备数字的量化、排序意义	有大小、顺序，可量化比较	考试分数（“85 分”“92 分”，可排序 “92 分＞85 分”）

两类数据的本质差异：
定性数据聚焦 “是什么类别”，仅用于区分属性
定量数据聚焦 “有多少 / 多大量”，可通过数值进行量化分析、排序比较
两者从 “类别属性” 和 “数值意义” 两个维度，构成了数据分类的基础逻辑！

3.区间宽度、频数密度

直方图用于数值型数据的分组频数可视化，多数场景下区间宽度相同（如 [1,5]、[5,10]，宽度为 5）；但部分场景会出现区间宽度不同（如游戏时间的 [0-1]、[1-3]、[5-10] 等区间），如下图：

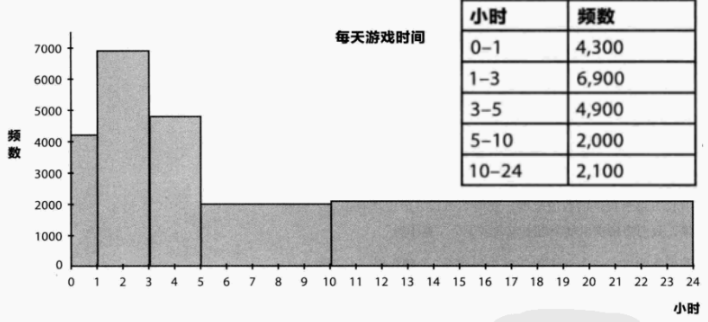
问题指出：传统直方图若直接以 “频数” 为高度，会因区间宽度不同导致视觉误导（如 “1-3” 区间频数高但宽度大，实际密集度并不突出）

解决办法：此时需遵循 “长方形面积与频数成比例”的原则 —— 即通过频数密度（即频数 ÷ 区间宽度）来标准化，确保不同宽度区间的对比公平性【长方形面积直接反映频数的多少】

计算公式：长方形面积 = 长方形高度（频数密度） × 区间宽度 = （频数 ÷ 区间宽度）× 区间宽度 = 频数

解决效果：优化后以 “频数密度” 为高度，长方形面积与频数成比例，能真实反映各区间的数据密集程度（如 “0-1” 区间频数密度最高，说明该区间数据最密集

指标	定义	与 “区间宽度” 的关系	意义
频数	某区间内原始数据的绝对出现次数	直接相关（宽度越大，频数可能越高）	反映区间数据的 “绝对数量”
频数密度	单位区间宽度对应的频数（频数 ÷ 区间宽度）	无关（仅反映数据 “密集程度”）	消除区间宽度影响，实现不同区间的公平对比

直方图宽度区间的同与不同：
宽度区间相同：长方形的高度与频数成比例（即:高度=频数）
因为区间宽度相同，长方形面积 = 高度 × 宽度（宽度固定），所以面积直接由高度决定，此时高度就可以直接反映频数的多少，即高度与频数成比例
宽度区间不同：长方形的面积与频数成比例（即:面积=频数）
因为区间宽度不同，长方形面积 = 高度(频数密度) × 区间宽度 = 频数（详情看上述计算公式）

本章涉及的图形：折线图、饼图、垂直条形图、水平条形图、分段条形图、堆积条形图、直方图、累计折线图

二、集中趋势的量度

1.均值、偏斜数据

指标	定义与计算公式	特点
均值		反映数据 “平均水平”，但易受异常值影响
中位数	数据排序后位于中间位置的数值（若数据量为偶数，取中间两个数的均值）	若数据都是两边极端的情况下，可能具有误导性（如100，100，20）
众数	数据集中出现次数最多的数值，可用于类别数据	是数据集的 “典型值”，必然属于数据集

指标

定义与计算公式

特点

均值

反映数据 “平均水平”，但易受异常值影响

中位数

数据排序后位于中间位置的数值

（若数据量为偶数，取中间两个数的均值）

若数据都是两边极端的情况下，可能具有误导性（如100，100，20）

众数

数据集中出现次数最多的数值，可用于类别数据

是数据集的 “典型值”，必然属于数据集

异常值：与其他数据格格不入的极高或极低的数值
偏斜数据：异常值会 “拉扯” 均值，导致数据分布偏斜，此时均值会失去代表性，存在误导性

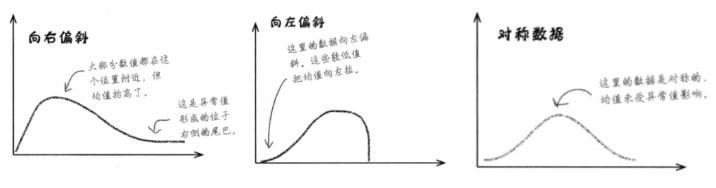
分布类型	形态特点	均值、中位数、众数的关系
右偏（长尾向右）	存在大异常值，右侧拖 “尾巴”	均值 > 中位数 > 众数
左偏（长尾向左）	存在小异常值，左侧拖 “尾巴”	均值 < 中位数 < 众数
对称分布	无明显偏斜，两侧形态对称	均值 = 中位数 = 众数

2.含含糊糊的平均数

推理复盘：某公司薪酬分布：大部分员工周薪 500 美元，少数经理薪资较高，首席执行官周薪 49,000 美元。不同角色对 “平均薪水” 的解读产生分歧：

工人认为 “平均薪水 2,500 美元”（实际用了中位数，削弱了 CEO 高薪的影响）
经理认为 “平均薪水 10,000 美元”（实际用了均值，CEO 高薪使均值虚高）
CEO 认为 “平均薪水 500 美元”（实际用了众数，500 美元是出现次数最多的薪资）

推理总结：“平均数” 是集中趋势指标的统称，包含均值、中位数、众数，需根据数据特点选择：

当数据无异常值、对称分布时，均值能较好代表整体水平
当数据存在异常值（如本例中 CEO 高薪）时，中位数更能反映大多数人的真实情况，避免被极端值误导

三、分散性与变异性的量度

1.全矩、四分位矩

指标	计算公式	特点与局限性
全距（极差）	全距 = 上界（最大值）- 下界（最小值）	示例：球员得分 7、9、9、10、11、13，全距 = 13-7=6 特点：仅描述数据 “宽度”，易受异常值误导，无法反映数据在上下界间的分布形态
四分位距（IQR）	四分位距 = 上四分位数（Q3）- 下四分位数（Q1）【Q1 为下四分位数，Q3 为上四分位数，中间 Q2 为中位数】	仅关注数据中心 50% 的部分，较少受异常值影响，是 “不易被异常值干扰的迷你距”

指标

计算公式

特点与局限性

全距

（极差）

全距 = 上界（最大值）- 下界（最小值）

示例：球员得分 7、9、9、10、11、13，全距 = 13-7=6

特点：仅描述数据 “宽度”，易受异常值误导，无法反映数据在上下界间的分布形态

四分位距

（IQR）

四分位距 = 上四分位数（Q3）- 下四分位数（Q1）

【Q1 为下四分位数，Q3 为上四分位数，中间 Q2 为中位数】

仅关注数据中心 50% 的部分，较少受异常值影响，是 “不易被异常值干扰的迷你距”

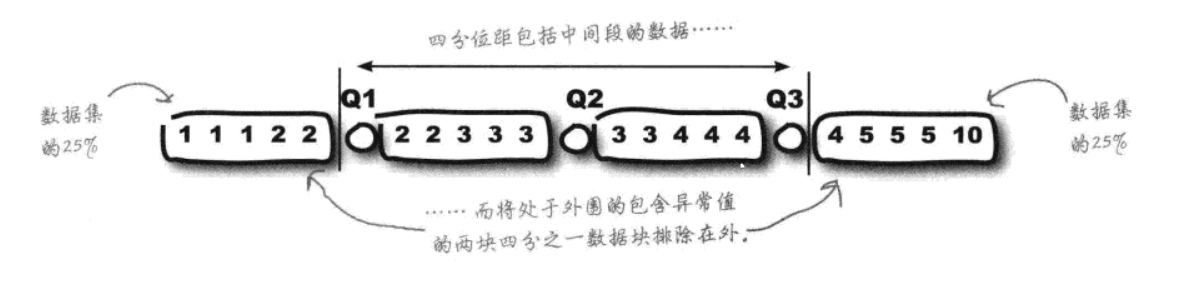
全矩和四分位矩的区别（应对异常值的逻辑）：
全距的问题：极易受异常值影响，只要有一个极端值，结果就会 “天差地别”
四分位距的优势：只关注数据中央50%区间，排除了两端异常值干扰，更能反映数据的核心离散程度

2.百分位数、箱线图

① 百分位数 $P_k$

指标定义：第k百分位数是位于数据范围k%处的数值；四分位数是特殊的百分位数（Q1=P25，Q3=P75）
计算规则：若有n个数据，第k百分位数的位置为 $\frac{k* n}{100}$ ，结果向上取整
案例分析：125 个数求第 30 百分位数，位置 $\frac{k*n}{100} = \frac{30*125}{100} = 37.5$ ，向上取整为38，即第38位的数值为第30百分位数

② 箱线图（箱形图）

指标定义：离散程度的可视化工具，可展示全距、四分位距及中位数
图形解读：
- 箱子两端：下四分位数（Q1）和上四分位数（Q3），箱内横线为中位数（Q2）；
- 箱子外的 “whisker（须）”：延伸至下界（最小值）和上界（最大值），展示全距。

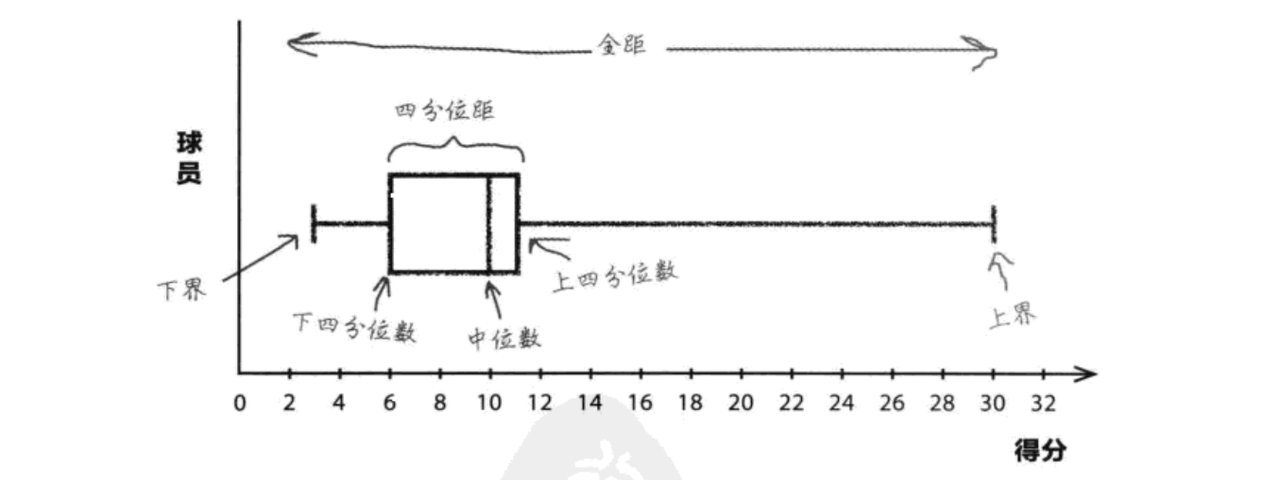
案例分析：

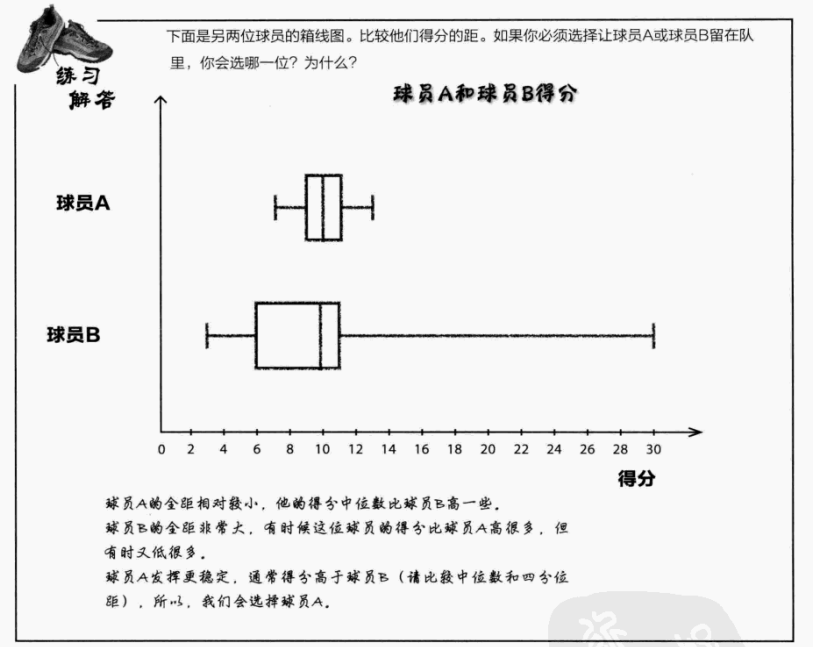
球员 A：全距小，中位数高，四分位距窄→ 得分稳定且整体水平高

球员 B：全距大，得分波动剧烈，虽有时得分很高，但低分时也很低→ 稳定性差

结论：选择球员 A，因其得分更稳定且中位数更高

离散程度分析的局限与价值：
全距和四分位距仅能反映 “最大值与最小值的差值”，但无法体现 “极值出现的频率” 或 “数据中心区域的分布密度”。
因此，在分析离散性时，需结合百分位数、箱线图等工具，从 “数值差异” 和 “分布形态” 两个维度全面解读数据

3.方差、标准分

本章的方差、标准差等计算针对的对象是：样本数据（实际的结果，即已经发生，是具体数值）

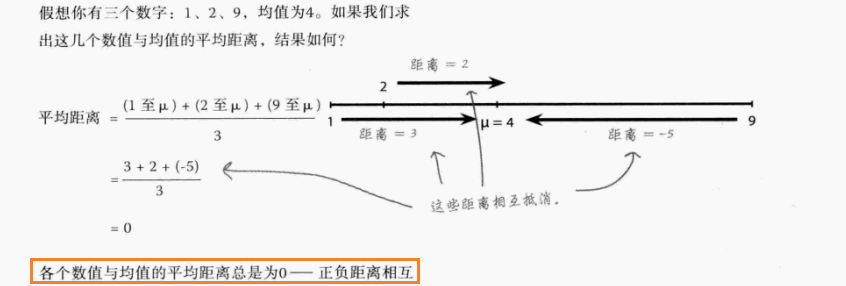
① 平均距离

指标定义：数值与均值的距离值的求和计算，实际上会因正负抵消而恒为0，无法反映离散程度（如下图）

② 方差 $\sigma^2$

指标定义：数值与均值距离的平方数的平均值，用于度量数据离散性
计算公式： 方差 $\sigma^2 = \frac{\Sigma(x-u)^2}{n}=\frac{\Sigma x^2}{n}-u^2$ （后者计算更简便，u 为均值，n 为数据量）

③ 标准差 $\sigma$

指标定义：方差的平方根，描述 “典型值与均值的距离”，比方差更易理解
计算公式： 标准差 $\sigma = \sqrt{\sigma ^2}$
指标意义：标准差越小→数据离均值越近→变异越小→稳定性越高
标准差越大→数据离均值越远→变异越大→稳定性越低

【注：标准差 $\sigma$ 的最小值为 0（即当所有数据等于均值时），另无负值】

④ 标准分z

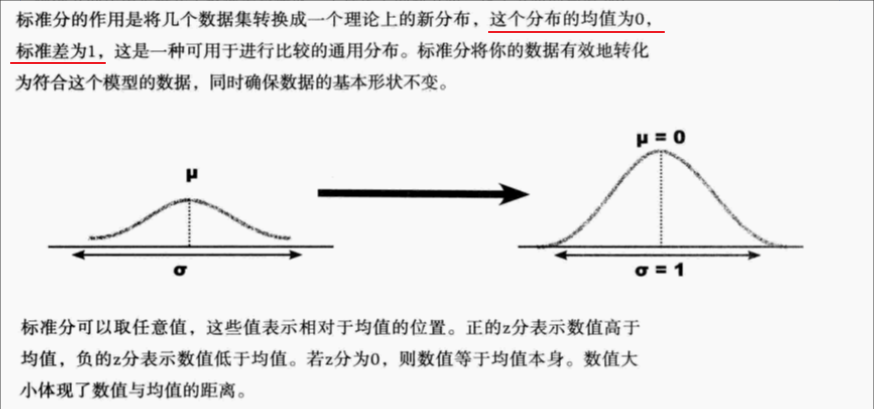
指标定义：用于比较均值和标准差不同的数据集
计算公式：标准分 $z= \frac{x-u}{\sigma}$ （x 为待比较数值，u 为数据集均值， $\sigma$ 为数据集标准差）
指标意义：提供了一种对不同数据集的数据进行比较的办法，这些不同数据集的均值和标准差甚至都各不一样。根据标准分z的计算方法，可以把这些数值视为来自同一个数据集或数据分布，从而进行比较

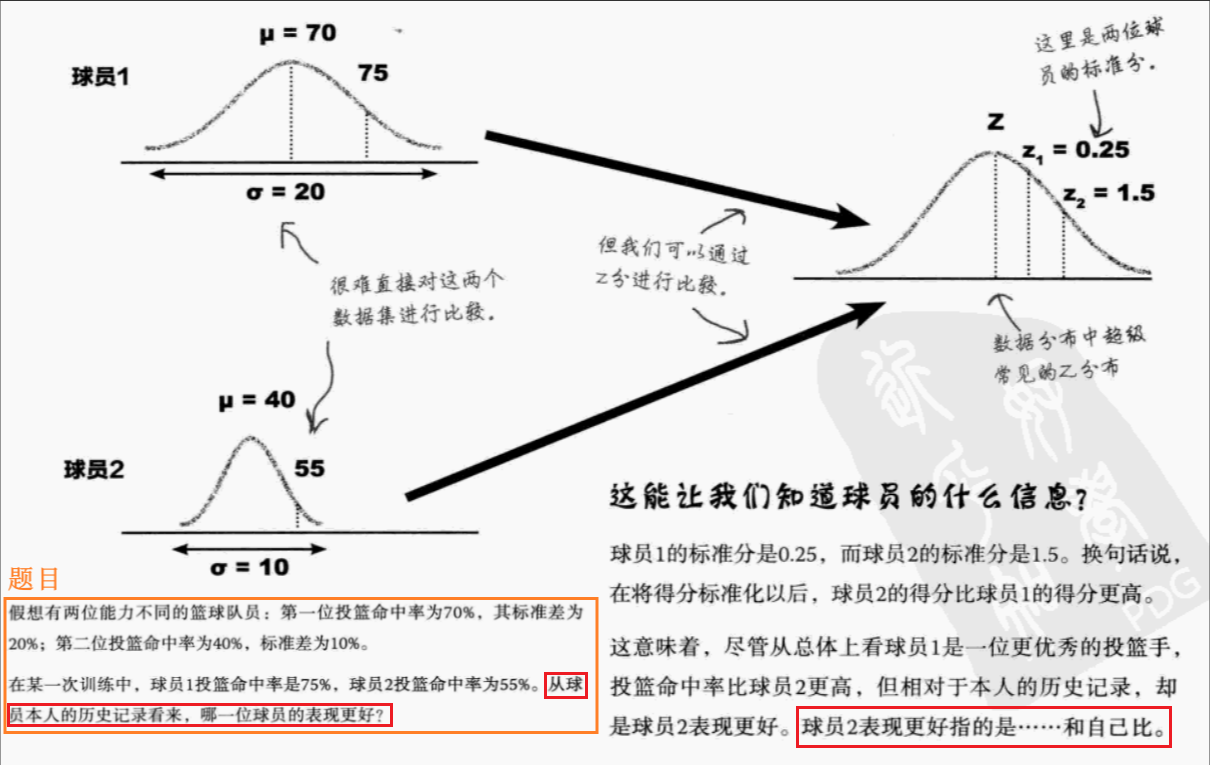
案例分析：（请联想z的计算公式去思考z的含义）

方差和标准差都能量度数据的分散程度，那么它们与全距有何区别？
全距是一种极其简单的量度数据分散程度的方法，它指出最大值和最小值之间的差值，但仅此而已。无法看出数据在这个差值范围内的聚散情况
用方差和标准差方法量度数据的变异性和分布形态则效果好得多，因为这二者考虑了数据的聚散情况，它们关注的是典型情况下的数值与数据中心的距离
标准分是什么？标准分和异常值检测有什么关系吗?
标准分是利用均值和标准差，将一个数据集中的各个数值转化为更通用的分布形态，同时确保数据的基本形状不变
标准分是对不同数据集中的数值进行比较的一种方法--即使各个数据集的均值和标准差各不相同也能进行比较，这是一种量度相对排名的方法
可以凭主观判断确定异常值，但有时候可以将异常值定义为偏离均值三个标准差的数值，即$3\sigma$（3西格玛）原则进行异常值处理

方差、标准差是从 “数值与均值的距离” 角度精准度量离散程度
标准分则突破数据集差异，实现跨场景的公平对比

四、概率计算

1.概率基础、对立事件

概念	定义与公式	说明
概率（P）	度量事件发生几率的数量指标，其量度尺度是0-1	0表示不可能发生，1表示必然发生
事件（A）	可指出发生可能性的 “事情”，是样本空间的子集	统计学中 “有概率可言的事情”
样本空间（S）	所有可能结果的集合，即 “概率空间”	可能发生的事件都是S的子集
事件概率公式	A事件的概率P(A) = \frac{发生事件A的可能数目}{所有可能结果的数目}=\frac{n(A)}{n(S)}	基于 “等可能结果” 的古典概型计算
对立事件（A'）	“事件A发生”的对立事件是“事件A不发生”，用A'表示；$P(A') = 1 - P(A)$	对立事件必互斥，且并集∪为样本空间

2.相交与互斥、维恩图

运算	含义	符号
交集 ∩	“与”，事件A和B同时发生	A ∩ B
并集∪	“或”，事件A或B发生，即A与B两事件的所有要素	A ∪ B

维恩图（交集和并集）

$P(A\cap B) = P(A)+P(B)-P(A\cup B)$

$P(A\cup B) = P(A)+P(B)-P(A\cap B)$

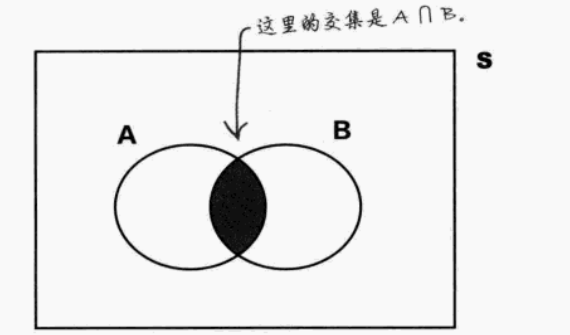
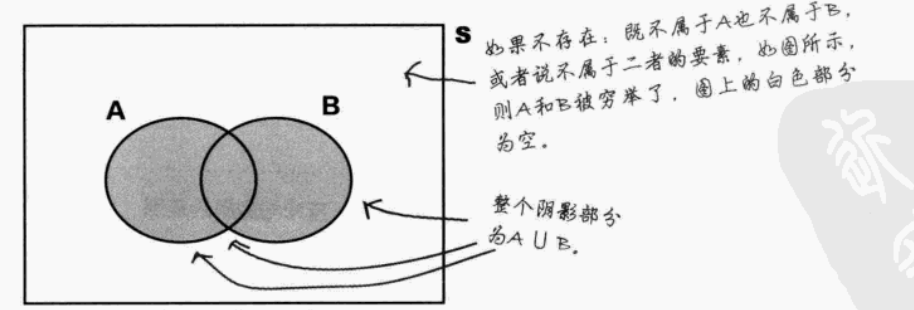
穷举事件：若P(A∪B) = 1，则说明事件A与事件B穷举，它们形成整个样本空间S，穷举了所有可能性
相交事件：如果事件A和事件B相交，则事件A和事件B有可能同时发生，即 $P(A\cap B) > 0$
互斥事件：如果事件A和事件B互斥，则事件A和事件B不可能同时发生，即 $P(A\cap B)=0$

互斥事件不一定是对立事件（对立事件需满足 “非此即彼” 且并集为样本空间）
但对立事件一定是互斥事件

3.条件概率、概率树图

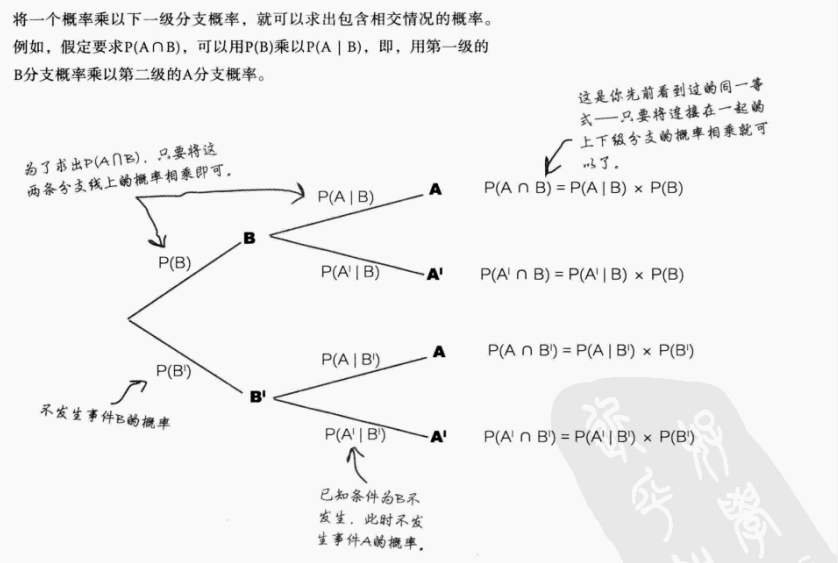
条件概率：以事件B发生为条件，事件A发生的概率，写为P(A|B)。计算公式如下：

$P(A|B) = \frac{P(A\cap B)}{P(B)}$ ⟹ $P(A\cap B) = P(B)*P(A|B)$

概率树图：可视化条件概率的方法，通过 “分支概率相乘” 计算交集概率，如下图：

4.全概率公式、贝叶斯定理

全概率公式：根据条件概率计算某个特定事件的全概率（总概率）

$P(B) = P(A)*P(B|A)+P(A')*P(B|A')$

（本质是将B的概率分解为 “A发生时B发生的概率” 与 “A不发生时B发生的概率” 之和）

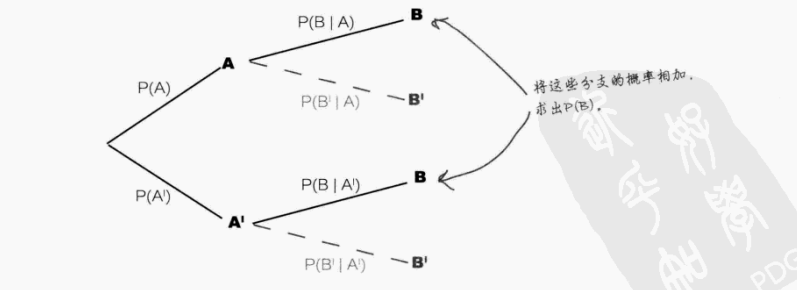
公式推理如下：

① 如图事件B发生的可能是在P(B|A)、P(B|A')这两种的情况，根据条件概率 $P(A|B) = \frac{P(A\cap B)}{P(B)}$ 可得：P(A\cap B) = P(A)*P(B|A)、P(A'\cap B)=P(A')*P(B|A')

② 根据维恩图理解P(A\cap B)、P(A'\cap B)这两概率的含义，如下图所示

事件A = 浅黄色部分 + 淡红色部分（重合） = A∩B' + A∩B

事件B = 浅紫色部分 + 淡红色部分（重合） = A'∩B + A∩B

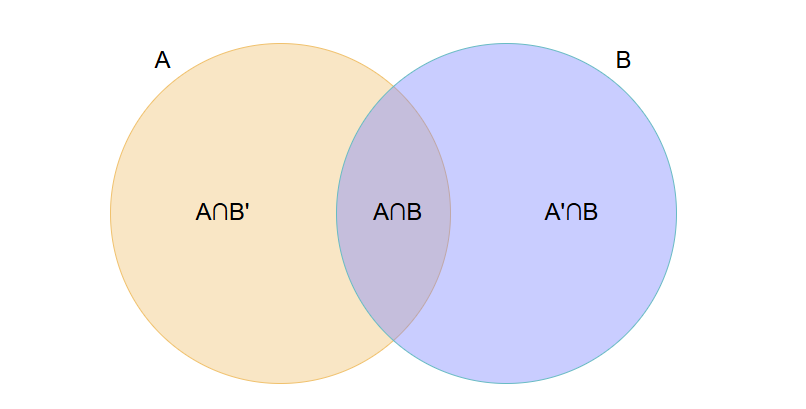
③ 根据①和②的分析可得，事件B的概率（即事件B的全概率公式）：

$P(B) = P(A\cap B) + P(A'\cap B) = P(A)*P(B|A)+P(A')*P(B|A')$

贝叶斯定理：用于 “由结果反推原因的概率”，即条件概率的逆运算，知P(B|A)得出P(A|B)

$P(A|B) = \frac{P(A)*P(B|A)}{P(A)*P(B|A)+P(A')*P(B|A')}$

分母是全概率公式（事件B的总概率），分子是 “事件A发生且B发生的概率”，从而得到 “已知B发生时，A发生的概率”

公式推理如下：

① 根据条件概率公式可得P(A|B) = \frac{P(A\cap B)}{P(B)},那需要求出P(A\cap B)、P(B)这两个概率值，而且已经知道P(B|A)、P(A)等相关条件的值，那可得P(A\cap B) = P(A)*P(B|A)

② 分母P(B)的值就是全概率公式P(B) = P(A\cap B) + P(A'\cap B) = P(A)*P(B|A)+P(A')*P(B|A')

③ 知道P(A|B)的分母和分子，那么直接代入即可得到贝叶斯定理的公式：

P(A|B) = \frac{P(A\cap B)}{P(B)}= \frac{P(A)*P(B|A)}{P(A)*P(B|A)+P(A')*P(B|A')}

什么时候使用全概率公式？什么时候使用贝叶斯定理？【应用场景】
全概率公式：已知 “原因的概率” 和 “原因导致结果的概率”，求 “结果的总概率”
贝叶斯定理：已知 “结果发生”，反推 “某原因导致该结果的概率”，适用于 “条件概率顺序相反” 的场景，可结合概率树辅助理解

5.相关事件、独立事件

① 相关事件

指标定义：若事件间互有影响，则为相关事件，即P(A|B) ≠ P(A)【事件 B 的发生会改变事件 A 的概率】
案例分析：（一轮游戏）共有白球和黑球共30个，其中黑球有18个，白球有12个。在黑球中，数字为奇数有10个，偶数的有8个。那么P(偶|黑) = 8/18 = 4/9；而P(偶) = 18/30 = 3/5，即 P(偶|黑) ≠ P(偶) → 相关事件

② 独立事件

指标定义：若事件间互不影响，则为独立事件，即P(A|B) = P(A)，且满足 $P(A\cap B) =P(A)*P(B)$
案例分析：（两轮有放回摸球）共有白球和黑球共30个，其中黑球有18个，白球有12个。在黑球中，数字为奇数有10个，偶数的有8个。P(黑|黑) =（P(黑)*P(黑)）/P(黑) = P(黑) = 3/5；第一轮的结果不影响第二轮的结果，则P(黑) = 3/5；即 P(黑|黑) = P(黑) → 独立事件

互斥与独立的关系：
若 A、B 是互斥事件 $P(A\cap B) =0$ ，则一定不是独立事件（因为A发生会导致B不发生，相互影响）
若 A、B 是独立事件 $P(A\cap B) =P(A)P(B)$ ，则一定不是互斥事件（除非 $P(A)=0$ 或 $P(B)=0$ ，否则交集概率不为 0）。

③ 案例分析

五、离散概率分布的应用

1.概率分布、期望、方差

概念	定义与说明
随机变量（X/Y）	可取一系列数值的变量，每个数值对应特定概率，用大写字母表示（如X或Y）
变量值（x/y）	随机变量的特定取值，用小写字母表示（如x或y）,P(X=x)则表示“变量X取特定数值x的概率”
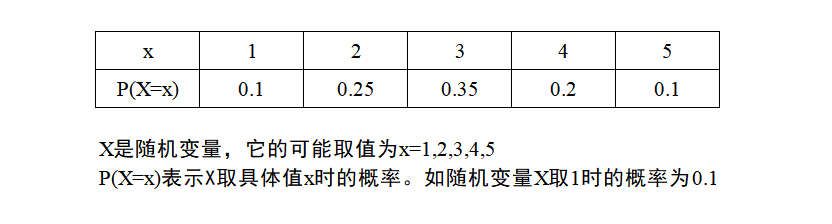
概率分布表	列出随机变量所有可能取值及对应概率的表格（如下图所示）

【补充说明：维恩图和概率树在计算概率时很有用；但对于概率分布来说，所有概率都早已计算好了】

本章期望、方差、标准差针对的对象是：离散型随机变量（还没发生，描述所有可能性，有概率信息）

① 期望E(X)

指标定义：离散型随机变量在大量重复试验下的平均结果，反映取值的集中趋势，通常写成E(X)或u，即均值
计算公式： $E(X) = u = \sum x * P(X=x)$
案例分析：如上面那张图表所例，它的期望值计算如下：（说明通过n次的抽取，抽到结果的均值为2.95）

$E(X) = u = \sum x * P(X=x) = 1*0.1+2*0.25+3*0.35+4*0.2+5*0.1=2.95$

② 方差Var(X)

指标定义：随机变量取值与期望距离的平方的加权平均，反映离散性，通常写成Var(X)
计算公式： $Var(X) = E(X-u)^2 = \sum(x-u)^2*P(X=x)$ 、标准差 $\sigma=\sqrt{Var(X)}$
指标意义：方差反映随机变量取值的离散程度，其大小对应不同的波动特征
方差越大→取值分布越分散，偏离均值的幅度大→收益 / 观测值波动性强
方差越小→取值越集中于均值附近→波动性低→系统稳定性高
案例分析：如上面那张图表所例，它的方差值计算如下：

$Var(X) = E[(X-u)^2] = \sum(x-u)^2*P(X=x) \\ =(1-2.95)^2*0.1+(2-2.95)^2*0.25+(3-2.95)^2*0.35+(4-2.95)^2*0.2+(5-2.95)^2*0.1\\=1.2475$

公式推理如下：

$Var(X) = E[(X-u)^2] = \sum (x-u)^2 *P(X=(x-u)^2)=\sum(x-u)^2*P(X=x)$

【1】随机变量的方差本质是“加权平均” ，而非样本数据的“算术平均”。样本数据的“除以 n”，是因为样本数据的 “权重” 是 “等权重”（每个数据的重要性相同），且权重和为n；而随机变量的 “概率” 是 “归一化权重”（和为1），加权求和后直接就是 “平均”，无需额外除法

【2】 P(X=(x-u)^2)和P(X=x)是一一对应的（即相同），原因是：当随机变量X取某一特定值(如x=1)，其概率 P(X=1)是确定的；而(x-u)^2由x唯一决定（如x=1对应唯一的（1-u)^2)。

离散型随机变量与样本数据的标准差和方差的核心区别：
样本数据本质：度量 “实际数据与均值的距离”，是算术平均（等权重，需除以数据量 n）【实际的结果，即已经发生，是具体数值】
离散随机本质：度量 “特定数值的概率分散情况”，是加权平均（概率为归一化权重，和为 1，无需额外除法）【还没发生，描述所有可能性，有概率信息】

③ 线性变换：当变量X按照aX+b的形式发生变换（a,b为常数），其计算方式如下：

期望：E(aX+b) =aE(X)+b

方差：Var(aX+b)=a^2Var(X)【常数b不影响离散程度】

2.独立观测值、线性组合

① 独立观测值

指标定义：（以 “赌局” 为例）在同一台赌博机上连续玩多局赌局时：
- 每一局称为一个事件，每一局的结果称为一个独立观测值（记为X_i）
- 每个观测值的期望和方差相同（因为每局独立且基于同一台赌博机，概率分布一致）
- 观测值数值有差别（每局结果不确定，收益不会完全一样），但概率分布完全相同
计算方法：

$$E(X_1+X_2+...+X_n) =nE(X)$$

$$Var(X_1+X_2+...+X_n) =nVar(X)$$

公式推理如下：

$$E(X_1+X_2+...+X_n) = E(X_1)+E(X_2)+...+E(X_n)=E(X)+E(X)+...+E(X)=nE(X)$$

$$Var(X_1+X_2+...+X_n) = Var(X_1)+Var(X_2)+...+Var(X_n)=...=nVar(X)$$

E(X1+X2)与E(2X)的区别：【看似相似，其实不然，它们是两个概念】
E(2X) ：对同一个变量的数值进行 “翻倍” 操作后求期望，变量只有一个，是数值层面的缩放
E(X1+X2)：观测两个独立的同分布结果后求综合期望，是两个独立事件的结果叠加，代表多局试验的总期望

案例分析：假设随机变量 X 的期望为E(X) = u，方差为 Var(X) = \sigma^2
E(2X) = 2E(X) = 2u ；Var(2X) = 4Var(X) = 4 * \sigma^2
E(X1+X2) = E(X1) +E(X2) = 2u ；Var(X1+X2) = Var(X1) + Var(X2) = 2 * \sigma^2
从期望结果看，二者在数值上相等；但从概念本质看，2X 是 “单个变量的数值缩放”，X1+X2 是 “两个独立变量的结果叠加”，逻辑完全不同
从方差结果看，更能体现二者的本质差异

② 多随机变量的线性组合