[优选算法专题五.位运算——NO.35~36 只出现一次的数字 II、消失的两个数字]

题目链接：

137. 只出现一次的数字 II

题目描述：

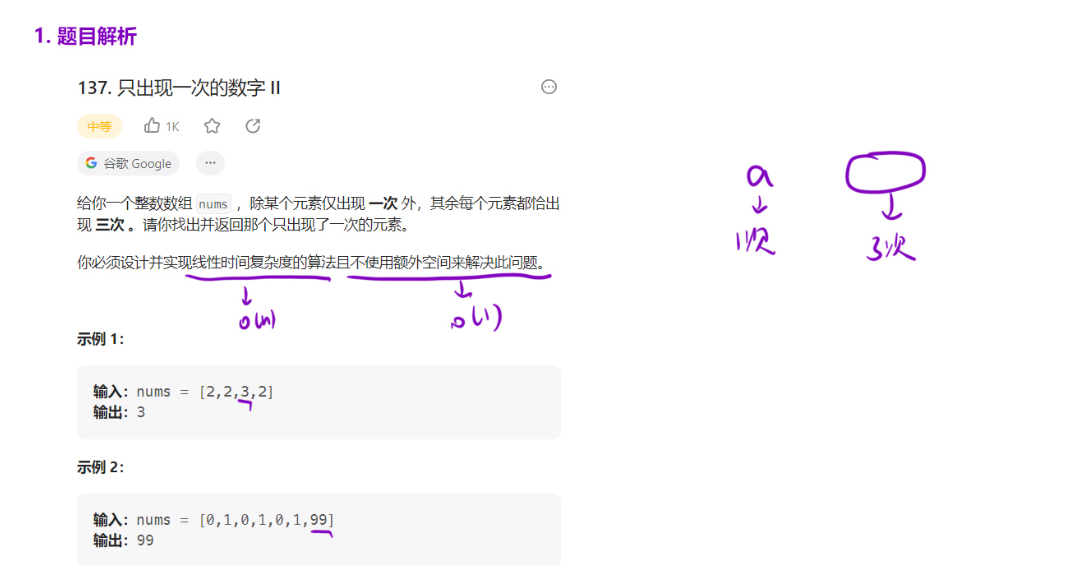
题目解析：

功能总结

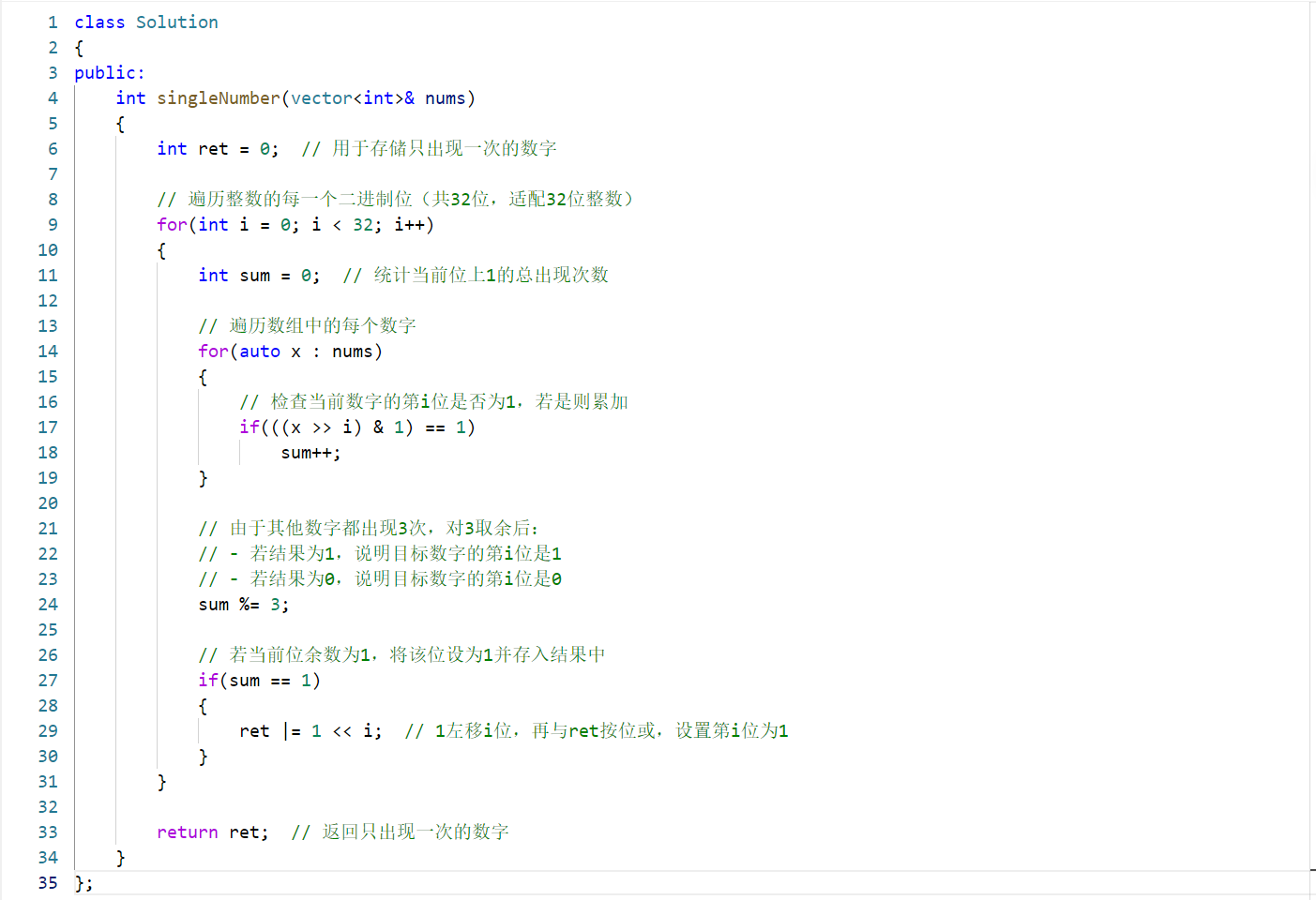
该代码用于解决「数组中除一个数字只出现一次外，其余数字都出现三次」的问题，核心思路是利用二进制位运算：

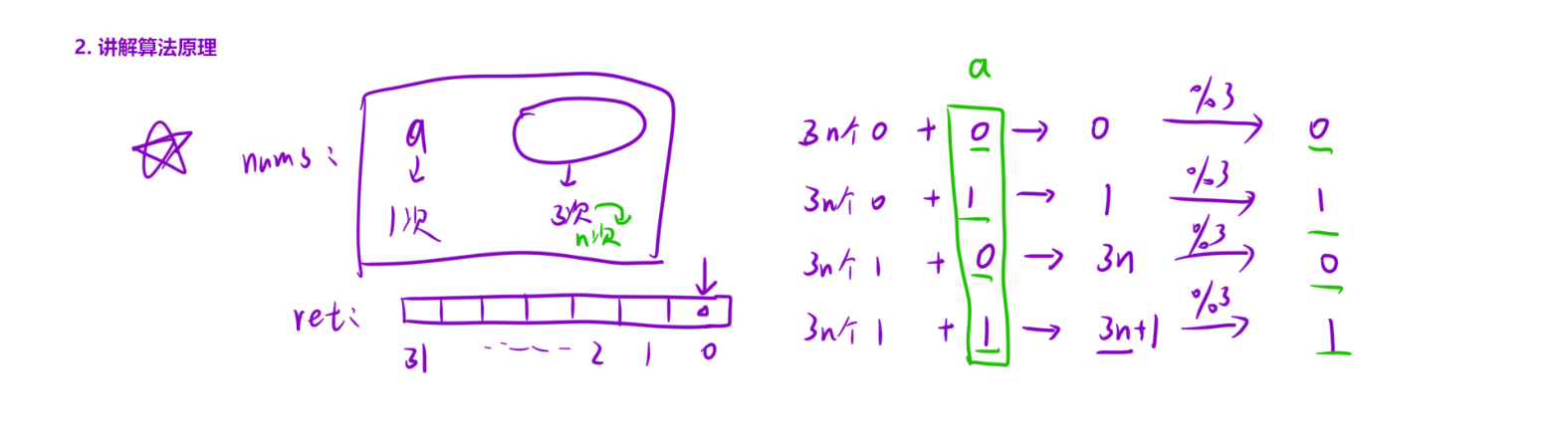
1. 原理：对于二进制的每一位，统计所有数字在该位上出现的总次数。由于除目标数字外的其他数字均出现 3 次，它们在该位的贡献总和一定是 3 的倍数（对 3 取余为 0）。因此，总次数对 3 取余的结果，就是目标数字在该位的值（0 或 1）。

2. 步骤：

   • 遍历 32 位整数的每一个二进制位；
   • 统计每个位上 1 的总出现次数；
   • 对次数取 3 的余数，确定目标数字在该位的值；
   • 拼接所有位的值，得到最终结果。

3. 时间复杂度：O (32×n) = O (n)，其中 n 为数组长度，32 是固定常数。

4. 空间复杂度：O (1)，仅使用常数额外空间。

---

题目链接：

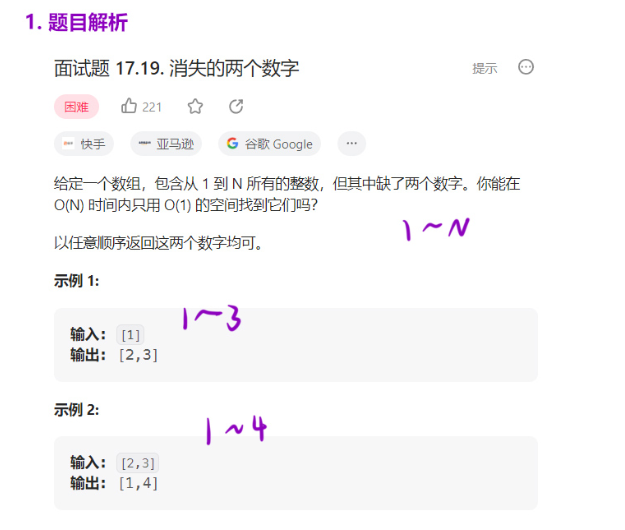
面试题 17.19. 消失的两个数字

题目描述：

功能总结

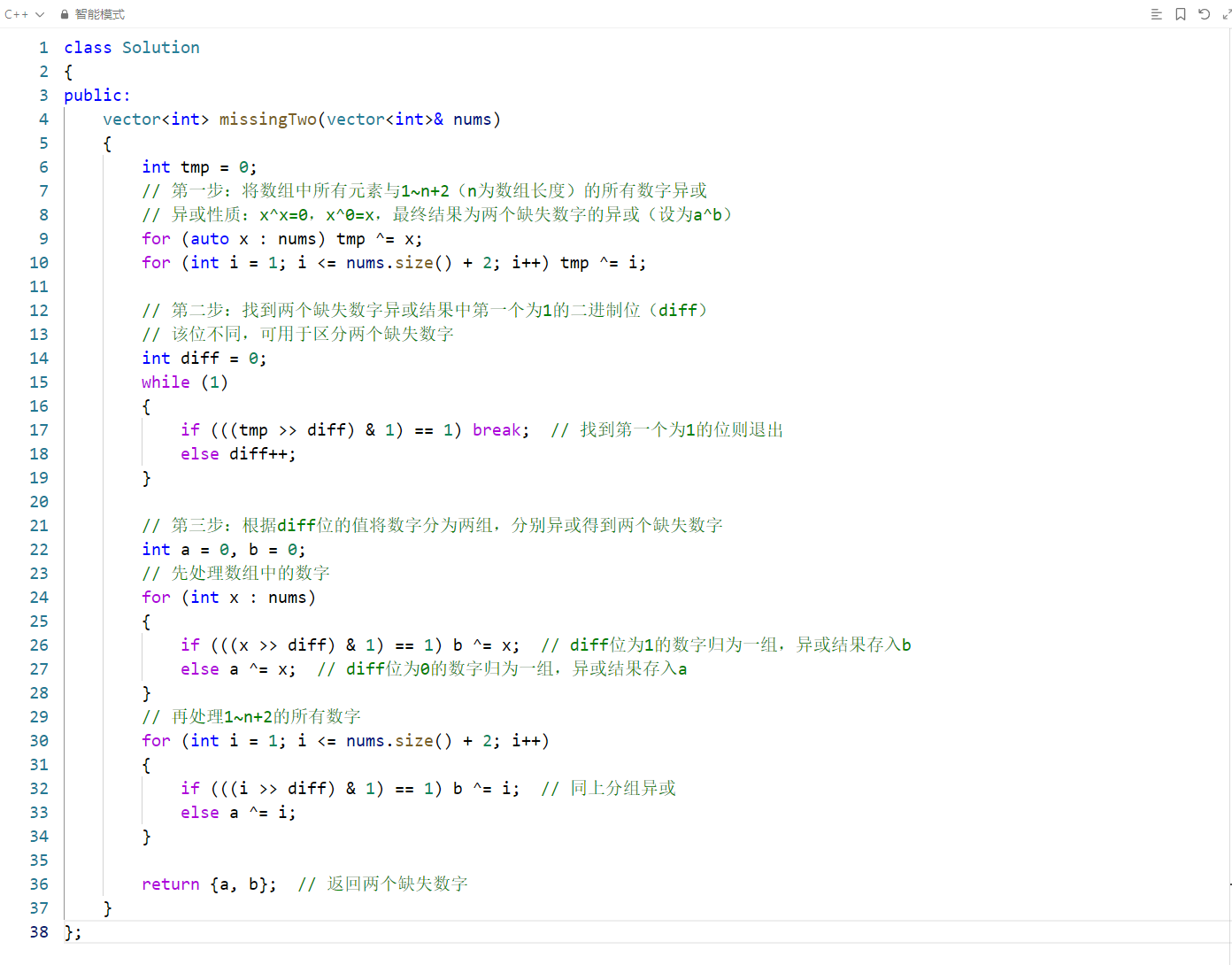
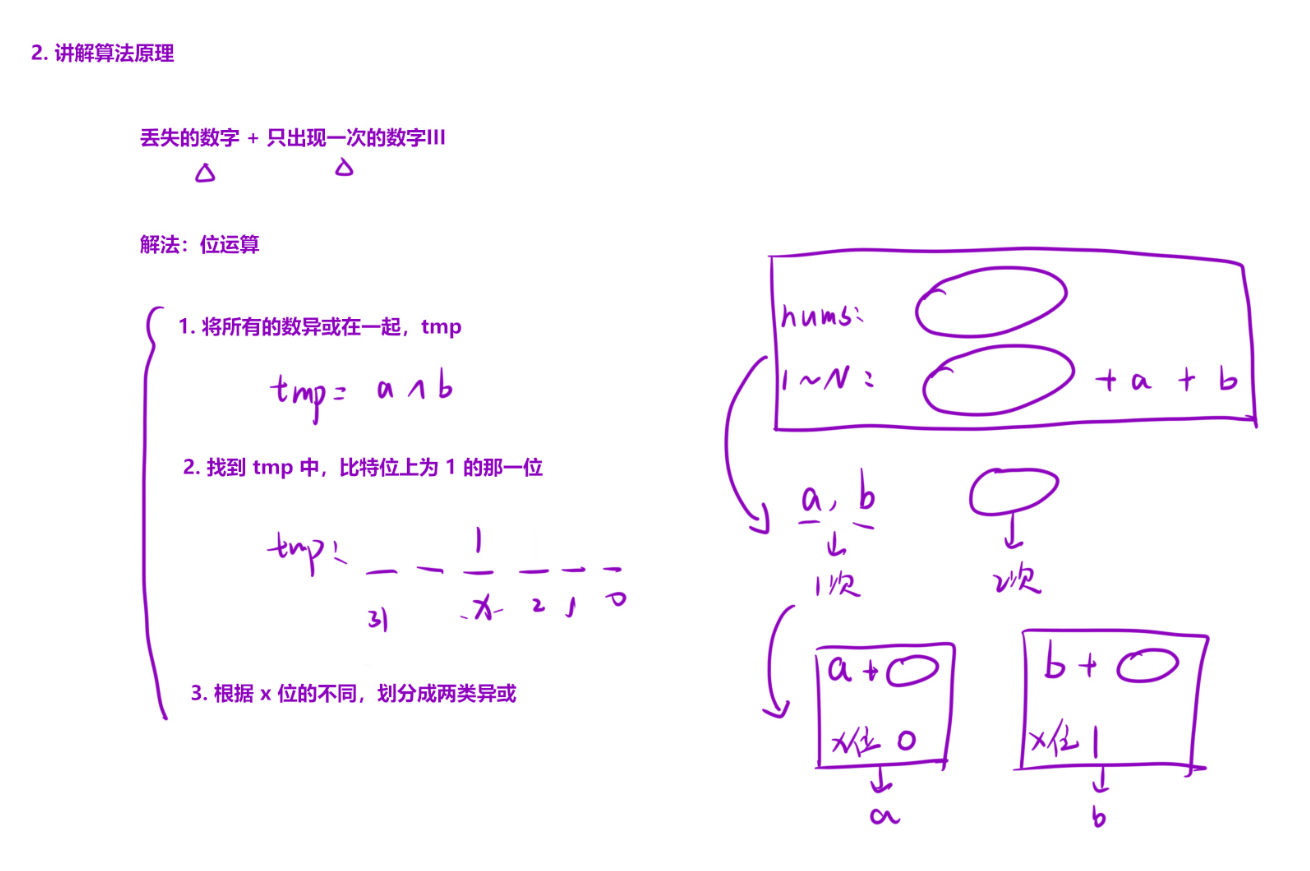
该代码用于解决「在包含 1~n+2 的数字中，缺失了两个数字，找出这两个缺失数字」的问题，核心思路是利用异或运算的性质：

1. 原理：

   • 异或运算具有 x^x=0、x^0=x、a^b^b=a 的性质；
   • 若将数组中所有元素与 1~n+2 的所有数字异或，最终结果为两个缺失数字的异或（a^b）；
   • 找到 a^b 中第一个为 1 的二进制位（diff），该位说明 a 和 b 在该位上的值不同（一个为 0，一个为 1）；
   • 根据 diff 位将所有数字分为两组，每组内异或后即可分别得到 a 和 b。

2. 步骤：

   • 计算数组元素与 1~n+2 的异或总和，得到 a^b；
   • 确定 a 和 b 的二进制差异位 diff；
   • 按 diff 位分组异或，分别得到两个缺失数字。

3. 时间复杂度：O (n)，其中 n 为数组长度，需遍历数组和 1~n+2 的数字。

4. 空间复杂度：O (1)，仅使用常数额外空间。