CCF-GESP 等级考试 2024年9月认证C++四级真题解析

2024年9月真题

一、单选题（每题2分，共30分）

正确答案：A
考察知识点：函数的定义与调用
解析：在 C++ 中，函数定义的格式为 “返回值类型 函数名 (参数类型 参数名，…) { 函数体 }”。选项 A 的int add(int a, int b) { return a + b; }符合 “返回整数值、接受两个整数参数” 的要求。答案为A。

正确答案：B
考察知识点：函数的定义与调用、形参与实参
解析：在 C++ 中，形参是函数定义时指定的参数（用于接收实参的值），实参是函数调用时传递给形参的具体值。选项 B 的描述符合这一关系。答案为B。

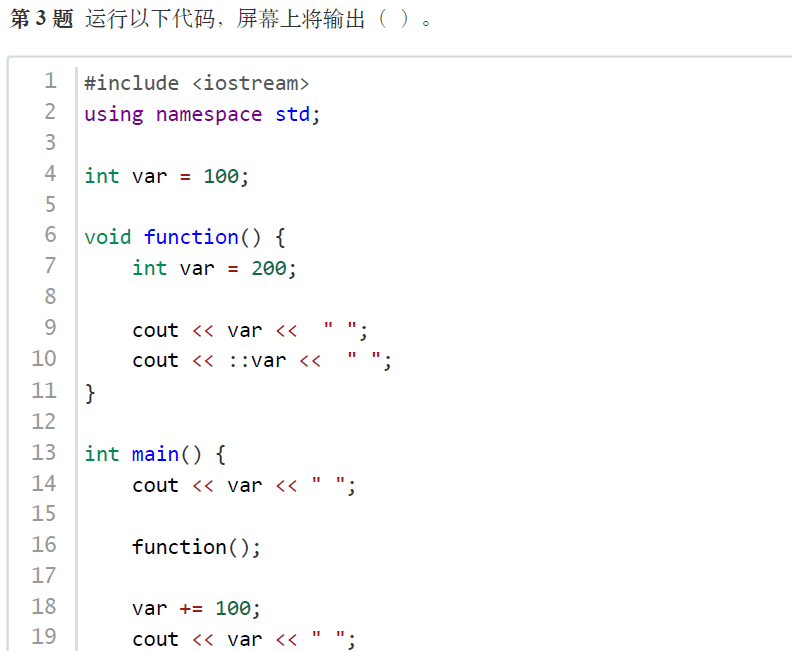
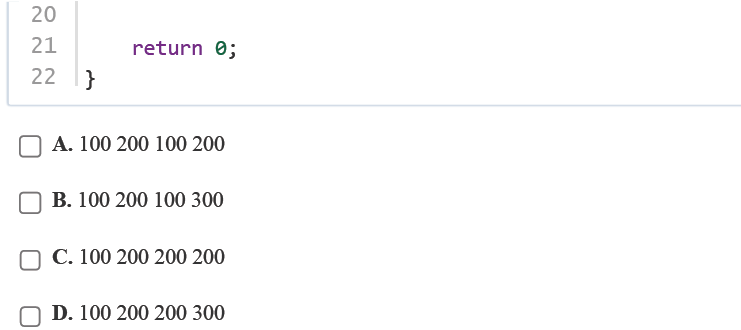
正确答案：A
考察知识点：函数的定义与调用、变量的作用域
解析：main函数中先输出var（全局变量，值为100）。
调用function函数时，输出局部var（200）和全局var（100， :; 访问到的是全局变量）。
main函数中var += 100后，全局var变为200，输出200。
因此最终输出为100 200 100 200。答案为A。

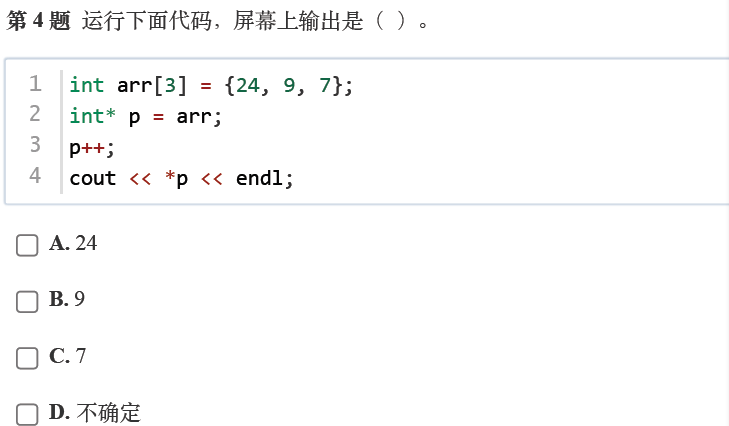
正确答案：B
考察知识点：数组、C++指针类型的概念及基本应用
解析：数组arr的首地址由p指向，执行p++后，p指向数组的第二个元素（即9）。*p取值该元素，因此输出9。答案为 B。

正确答案：D
考察知识点：C++指针类型的概念及基本应用
解析：代码中p初始指向x的地址，q指向y的地址。执行p = q;后，p的指向被修改为y的地址。答案为D。

正确答案：A
考察知识点：结构体
解析：在 C++ 中，结构体的正确定义格式为struct 结构体名 { 成员列表; };。选项 A 的struct student { char name[20]; int age; };符合要求，正确定义了包含name字符数组和age整数的student结构体。答案为A。

正确答案：B
考察知识点：二维数组与多维数组基本应用
解析：在 C++ 中，二维数组的声明格式为类型 数组名[行数][列数]。选项 B 的int arr[3][4];符合 “3 行 4 列” 的声明要求。答案为B。

正确答案：D
考察知识点：二维数组与多维数组基本应用
解析：二维数组arr[3][4]中，arr[0]是第 0 行的数组，包含 4 个int元素。每个int占 4 字节，因此arr[0]占用的内存为4 × 4 = 16字节。答案为D。

正确答案：A
考察知识点：递推算法
解析：阶乘的递推逻辑是result = result × i（初始result=1，依次乘以2,3,…,n）。选项 A 的result *= i;符合这一逻辑。答案为A。

正确答案：B
考察知识点：排序算法
解析：排序算法的稳定性：排序算法执行后，原始数组中相等元素的相对顺序保持不变，则该算法为稳定排序；反之则为不稳定排序。答案为B。

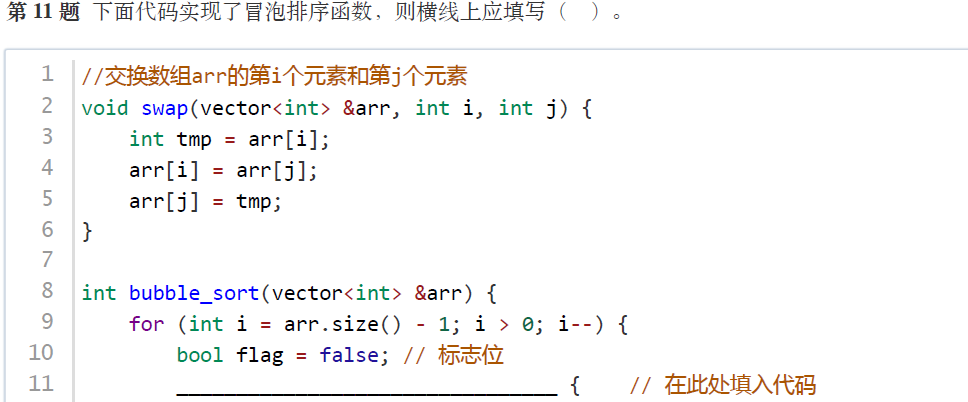
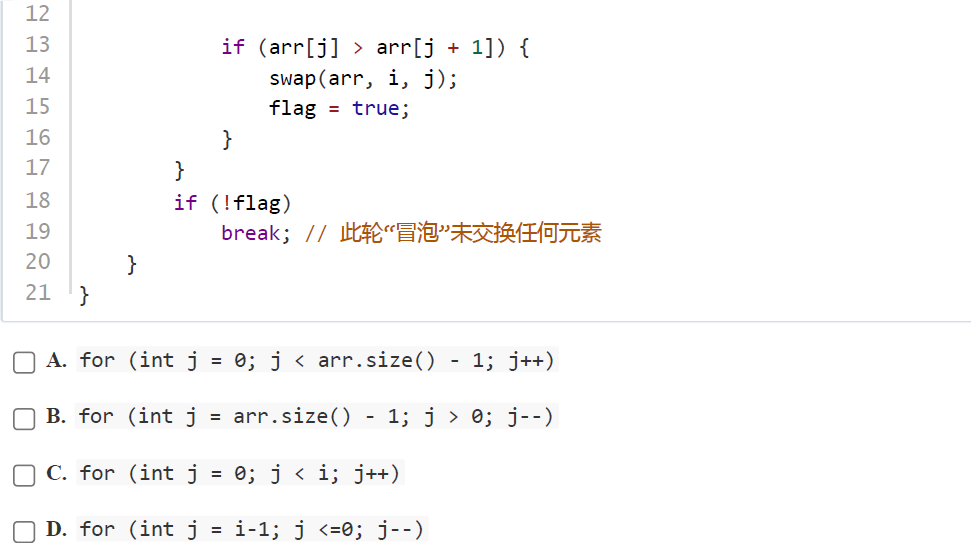
正确答案：C
考察知识点：排序算法
解析：冒泡排序的核心思想是：通过重复遍历待排序序列，每次比较相邻的两个元素，若顺序错误则交换它们的位置，直到没有元素需要交换为止。
冒泡排序的内层循环需遍历到当前未排序区间的末尾（由外层循环变量i控制）。选项 C 的for (int j = 0; j < i; j++)符合逻辑：每次外层循环i递减，内层循环遍历0到i-1的区间，对相邻元素进行比较交换。答案为C。

正确答案：A
考察知识点：排序算法、简单算法复杂度的估算
解析：该冒泡排序代码的时间复杂度分析如下：
最坏情况与平均情况：外层循环执行 n−1 次（n 为数组元素个数），内层循环在第 i 次外层循环时执行 i 次。总操作次数为 1+2+⋯+(n−1)= n(n−1)/2，因此时间复杂度为 $O(n^2)$。
最好情况：若数组已完全有序，内层循环的flag会提前终止循环，此时只需遍历一次数组，时间复杂度为 $O(n)$。
综上，该冒泡排序的平均、最坏时间复杂度为 $O(n^2)$，最好时间复杂度为 $O(n)$。答案为A。
对排序算法复杂度非常熟悉的同学，本题可直接作答。

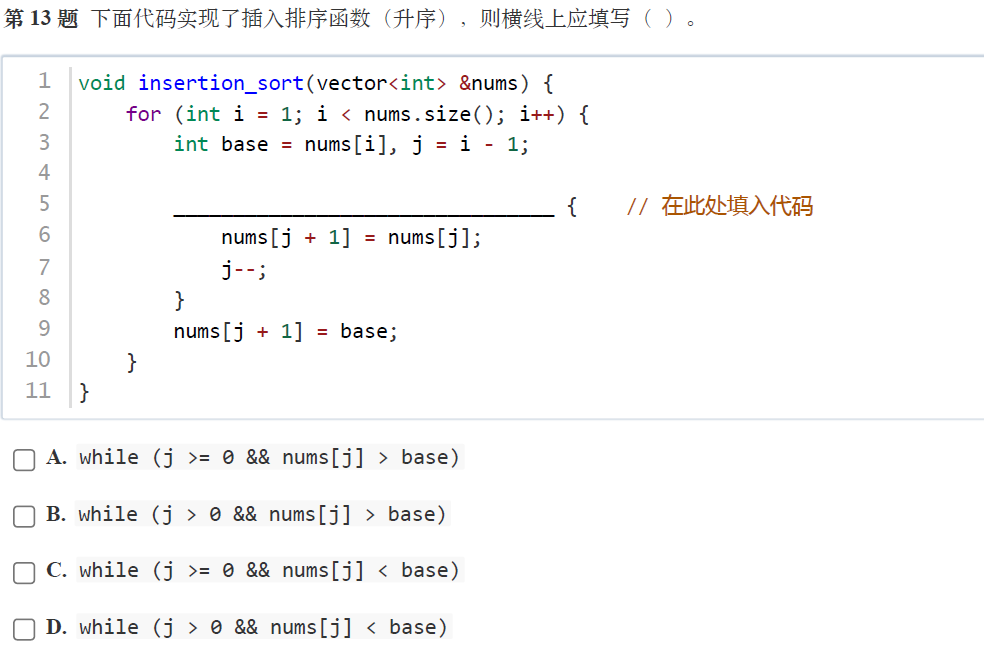
正确答案：A
考察知识点：排序算法
解析：插入排序的算法思想是：将待排序数组分为已排序区间和未排序区间，初始时已排序区间只有第一个元素。然后依次从未排序区间取出元素，插入到已排序区间的合适位置，使已排序区间始终保持有序，重复此过程直到未排序区间元素为空，最终得到有序数组。
插入排序的核心逻辑是：对于当前元素base，向前遍历已排序区间，当nums[j] > base且j ≥ 0时，将nums[j]后移。选项 A 的while (j >= 0 && nums[j] > base)符合这一逻辑。答案为A。

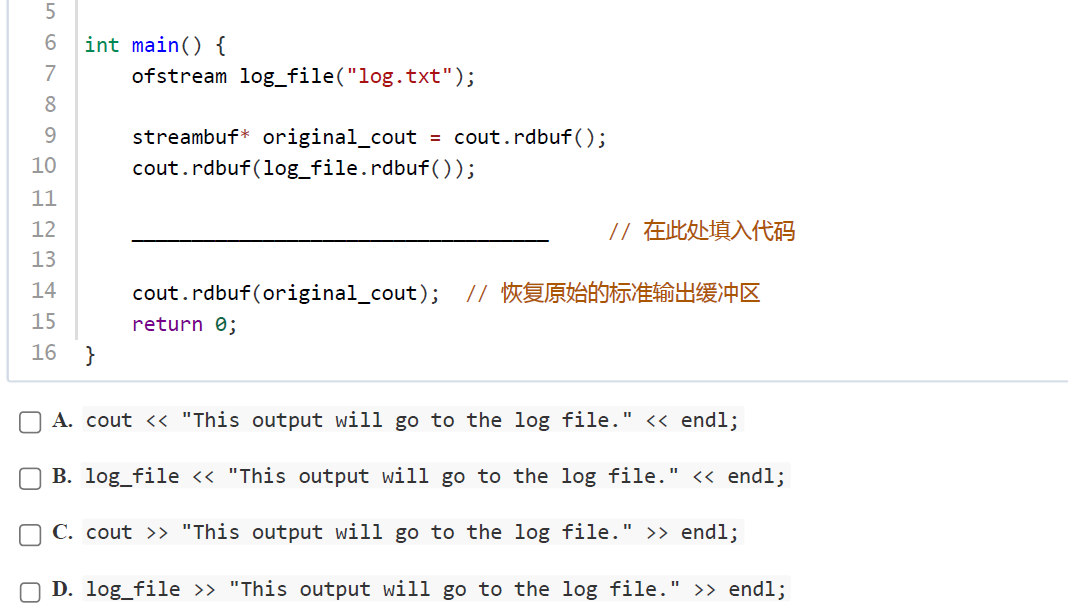
正确答案：A
考察知识点：文件重定向与文件读写操作
解析：代码中通过cout.rdbuf(log_file.rdbuf())将cout的输出缓冲区重定向到log_file（对应log.txt文件）。因此，使用cout输出的内容会写入log.txt，选项 A 的cout << “This output will go to the log file.” << endl;符合要求。答案为A。

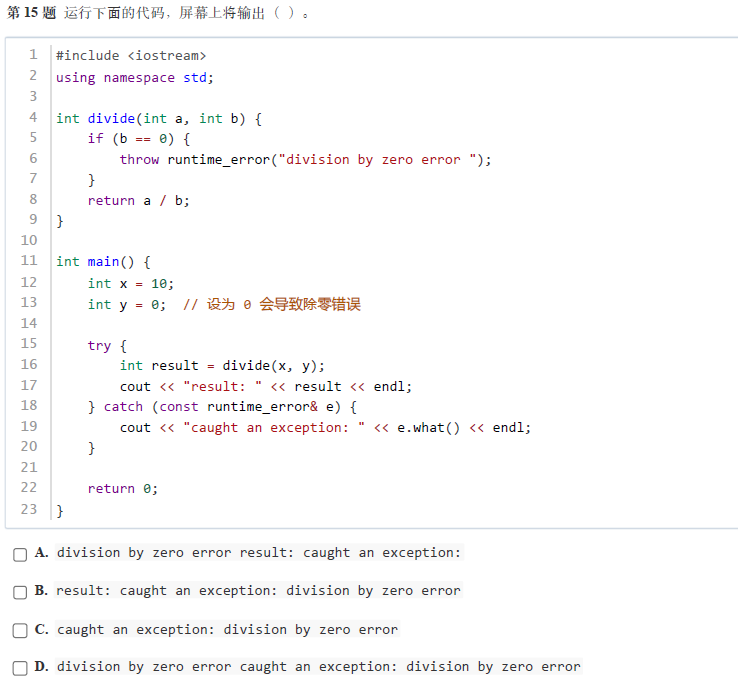
正确答案：C
考察知识点：异常处理
解析：代码中y=0，调用divide(x,y)时触发除零异常，抛出runtime_error("division by zero error “)。catch块捕获该异常，输出"caught an exception: division by zero error”。答案为C。

二、判断题（每题2分，共20分）

正确答案：正确
考察知识点：C++指针类型的概念及基本应用
解析：代码中先定义int变量a并赋值10，再定义指针p并将其初始化为a的地址（&a），这是 C++ 中正确定义和初始化指针的方式。表述正确。

正确答案：正确
考察知识点：函数参数传递的概念
解析：在 C++ 中，引用是变量的别名，函数通过引用传递参数时，直接操作原变量的内存空间，因此允许函数修改传递给它的参数的值。表述正确。

正确答案：错误
考察知识点：C++指针类型的概念及基本应用
解析：指针的大小取决于系统的地址总线宽度（如 32 位系统指针占 4 字节，64 位系统占 8 字节），与所指向变量的数据类型大小无关。例如，int和double指针在同一系统中大小相同。表述错误。

正确答案：错误
考察知识点：二维数组与多维数组基本应用
解析：在 C++ 中，二维数组的行和列的大小在定义时都必须确定，不支持列的大小动态变化。例如int arr[3][4]，行3和列4都需在定义时明确。表述错误。

正确答案：正确
考察知识点：递推算法
解析：递推算法的核心思想就是通过已知的初始状态，逐步推导当前状态与前一个或几个状态的关系（如斐波那契数列中f(n) = f(n-1) + f(n-2)），从而求解问题。因此该描述符合递推算法的定义。表述正确。

正确答案：错误
考察知识点：排序算法
解析：排序算法的稳定性：排序算法执行后，原始数组中相等元素的相对顺序保持不变，则该算法为稳定排序；反之则为不稳定排序。
选择排序，将待排序数组分为「已排序区间」和「未排序区间」，初始时已排序区间为空。每次从未排序区间中找到最小（或最大）元素，将其与未排序区间的第一个元素交换位置，此时该元素加入已排序区间。重复此过程，直到未排序区间为空。
选择排序是不稳定的排序算法。例如数组 [2, 2, 1]，第一趟会将第 3 个1与第 1 个2交换，导致两个2的相对顺序改变。表述错误。

正确答案：错误
考察知识点：排序算法
解析：插入排序的算法思想是：将待排序数组分为已排序区间和未排序区间，初始时已排序区间只有第一个元素。然后依次从未排序区间取出元素，插入到已排序区间的合适位置，使已排序区间始终保持有序，重复此过程直到未排序区间元素为空，最终得到有序数组。
冒泡排序的核心思想是：通过重复遍历待排序序列，每次比较相邻的两个元素，若顺序错误则交换它们的位置，直到没有元素需要交换为止。
插入排序和冒泡排序的时间复杂度平均、最坏情况均为 $O(n^2)$（n 为元素个数）。二者时间复杂度等级相同，不存在 “插入排序时间复杂度总是比冒泡排序低” 的情况。表述错误。

正确答案：错误
考察知识点：异常处理
解析：在 C++ 中，若抛出异常后没有匹配的catch块捕获，程序会立即终止，并调用std::terminate函数（默认行为是调用abort终止程序）。表述错误。

正确答案：错误
考察知识点：递推算法、简单算法复杂度的估算
解析：该代码采用递推法（迭代方式）求斐波那契数列，通过for循环从第 2 项迭代到第n项，循环次数为n-1次，时间复杂度为 $O(n)$（线性级），而非指数级。表述错误。

正确答案：正确
考察知识点：函数参数传递的概念、C++指针类型的概念及基本应用
解析：在main函数中，定义int a = 10，并让指针p指向a的地址（int* p = &a）。
调用point( p )时，函数内的*p就是a的值10，执行*p * 2后返回20。
*p = point( p ) 将a的值更新为20，最后cout << *p 输出 a 的当前值20。表述正确。

三、编程题（每题25分，共50分）

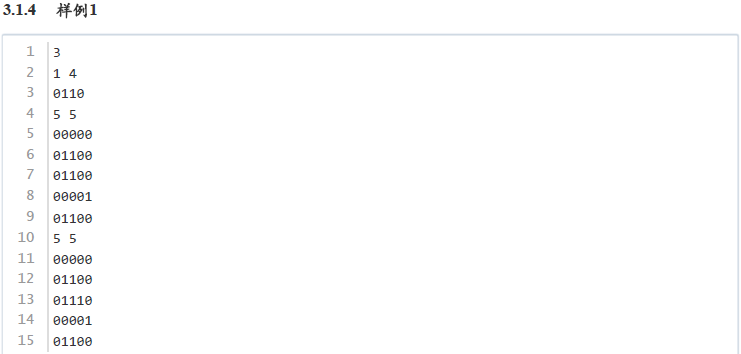
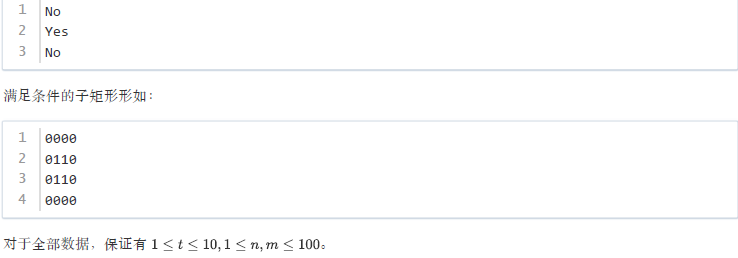
本题考察：模拟算法、枚举算法、多测试样例处理

枚举所有的4行4列子矩阵，判断其是否满足条件

#include<bits/stdc++.h>
using namespace std;
int t, n, m;
//预设4行4列满足条件的矩阵 
//1、矩形的第 1 行和第 4 行只包含白色格子；
//2、矩形的第 2 行和第 3 行，只有第 1 个和第 4 个格子是白色的，其余格子都是黑色的； 
char match[4][4]={{'0', '0', '0', '0'},{'0', '1', '1', '0'},{'0', '1', '1', '0'},{'0', '0', '0', '0'}};
char arr[101][101];
//通过和预设满足条件的矩阵进行比较，判断子矩阵是否满足条件 
bool check(int x1, int y1, int x2, int y2){for(int i=x1; i<=x2; i++){for(int j=y1; j<=y2; j++){if(arr[i][j] != match[i-x1][j-y1]) return false;}}return true;
}
int main() {cin>>t;while(t--) {cin>>n>>m;for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {cin>>arr[i][j];}}bool flag=0;//枚举所有的4行4列子矩阵//4行4列子矩阵左上角格子下标(x1, y1) for(int x1=1; x1+3<=n; x1++) {for(int y1=1; y1+3<=m; y1++) {	int x2=x1+3, y2=y1+3;  //4行4列子矩阵右下角格子下标(x2, y2)//检查子矩阵是否满足要求 if(check(x1, y1, x2, y2)){flag=true;break;}}if(flag) break;}if(flag) cout<<"Yes"<<endl;else cout<<"No"<<endl;}return 0;
}

提供另一种思路，利用前缀和求解，时间复杂度能再低一点，不过对本题来说，影响不大。

#include<bits/stdc++.h>
using namespace std;
int t, n, m, prefix[101][101];
char arr[101][101];
int main() {cin>>t;while(t--) {cin>>n>>m;memset(prefix, 0, sizeof(prefix));for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {cin>>arr[i][j];prefix[i][j] = prefix[i][j-1]+prefix[i-1][j]-prefix[i-1][j-1]+(arr[i][j]-'0');}}bool flag=false;//枚举所有的4行4列子矩阵//4行4列子矩阵左上角格子下标(x1, y1) for(int x1=1; x1+3<=n; x1++) {for(int y1=1; y1+3<=m; y1++) {int x2=x1+3, y2=y1+3; //4行4列子矩阵右下角格子下标(x2, y2)//计算子矩阵和 num int num = prefix[x2][y2]-prefix[x2][y1-1]-prefix[x1-1][y2]+prefix[x1-1][y1-1];//如果子矩阵和为4，且只有四个特殊位置为黑格子，说明满足要求 if(num == 4 && arr[x1+1][y1+1]=='1' && arr[x1+1][y2-1]=='1' && arr[x2-1][y1+1]=='1' && arr[x2-1][y2-1]=='1') {flag=true;break;}}if(flag) break;}if(flag) cout<<"Yes"<<endl;else cout<<"No"<<endl;}return 0;
}

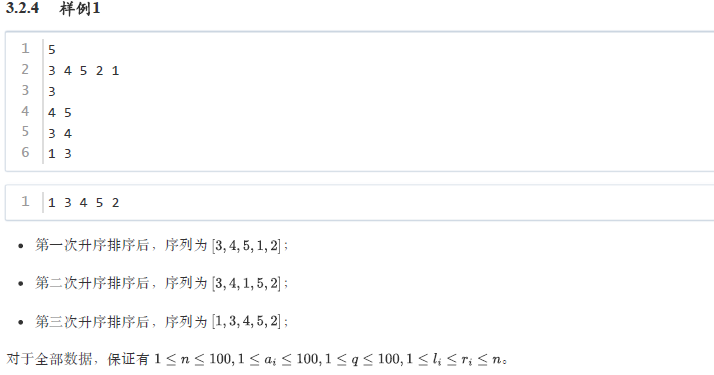
本题考察：排序算法、模拟算法。也是历史最简单了！！！

#include<bits/stdc++.h>
using namespace std;
int main() {int n, arr[101], q, l, r;cin>>n;for(int i=1; i<=n; i++) cin>>arr[i];cin>>q;while(q--){cin>>l>>r; sort(arr+l, arr+r+1); //使用sort函数进行区间排序 }for(int i=1; i<=n; i++) cout<<arr[i]<<" ";return 0;
}