视觉SLAM前置知识：相机模型

相机模型详解：从世界坐标到图像坐标的完整推导

视觉 SLAM 的核心之一就是重投影误差（Reprojection Error）。 要彻底理解它，首先必须理解相机模型（Camera Model）。 本篇文章从坐标系出发，详细讲解相机的几何关系、内外参数、投影模型、畸变、以及重投影误差的数学来源。

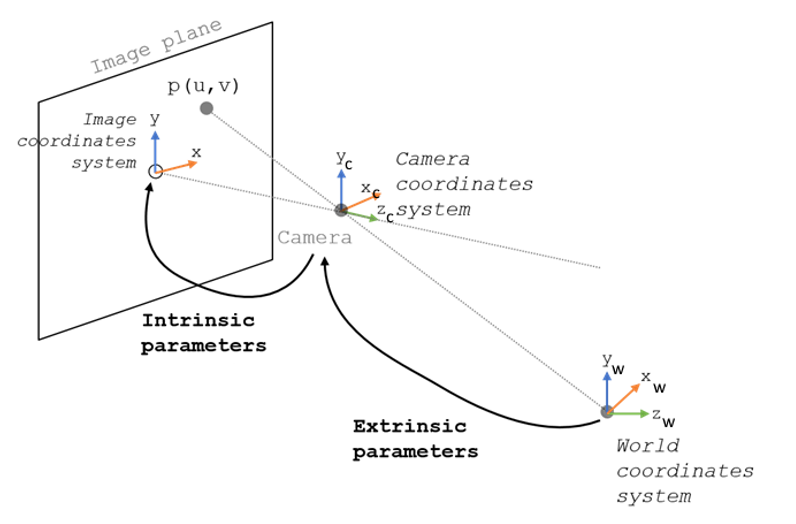
一、相机模型的核心思想

相机的作用：
把三维世界中的一个点 $P(X_w,Y_w,Z_w)$ 投影成二维图像平面上的一个像素点 $p(u,v)$。

这个过程主要分为两步：

1. 外参（Extrinsic Parameters）：描述世界坐标系 → 相机坐标系的变换；
2. 内参（Intrinsic Parameters）：描述相机坐标系 → 图像像素坐标系的变换。

二、坐标系的层次关系

相机模型中有三个主要坐标系：

1. 世界坐标系（World Coordinate System）
   表示现实世界中点的真实位置。
   一个点可表示为：
   $$P_w=\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

2. 相机坐标系（Camera Coordinate System）
   原点在相机光心，Z 轴指向成像方向（在视觉 SLAM、OpenCV、ORB-SLAM 等主流实现中，Z 轴是从相机出发，指向前方的世界）。
   点在相机坐标系下的表示为：
   $$P_c=\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

3. 图像坐标系（Image Coordinate System）
   原点位于图像平面中心，Z 轴垂直于成像平面。
   对应的像素坐标为 $p(u,v)$。

三、外参：世界坐标到相机坐标

世界坐标到相机坐标的转换由 旋转矩阵 ( R ) 和 平移向量 ( t ) 决定：

$$P_c=R{P}_w+t$$

用齐次坐标表示为：

$$\left[\begin{array}{c}{P}_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$

这部分称为 外参矩阵，代表相机在世界中的位姿。

四、透视投影模型（Pinhole Model）

在相机坐标系下，点 $P_c(X_c,Y_c,Z_c)$ 投影到成像平面上：

$$x=\frac{X_c}{Z_c},y=\frac{Y_c}{Z_c}$$

这里的 $(x,y)$ 是归一化平面坐标（焦距 = 1）。

五、内参：相机坐标到像素坐标

相机的内参矩阵$K$ 定义了从归一化平面坐标到图像像素坐标的变换：

$$K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

其中：

• $f_x=f/d_x$：焦距与像素比例（x方向）
• $f_y=f/d_y$：焦距与像素比例（y方向）
• $(c_x,c_y)$：主点（principal point）坐标（相机的光轴（即相机坐标系的 Z 轴）与图像平面（成像平面）相交的那个点）

将其应用到归一化坐标上：

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}{f}_{x}x+c_x\\ f_{y}y+c_y\\ 1\end{array}\right]$$

六、整体投影方程

综合外参与内参，完整的相机投影模型为：

$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K[R|t]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

其中 $s=Z_c$是尺度因子。

七、畸变模型（Distortion Model）

真实镜头会引入畸变，一般分为两种：

1. 径向畸变（Radial）：
   $$x_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$
   $$y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$
   其中 (r^2 = x^2 + y^2)。

2. 切向畸变（Tangential）：
   $$x^{\prime }=x+2p_{1}xy+p_2(r^2+2x^2)$$
   $$y^{\prime }=y+p_1(r^2+2y^2)+2p_{2}xy$$

最终像素坐标由畸变修正后的坐标计算得来。

八、重投影误差（Reprojection Error）

现在我们就能定义视觉 SLAM 优化的核心目标函数——重投影误差。

设：

• 实际观测到的像素坐标为 ${\mathbf{x}}_{i,k}^{obs}$
• 根据当前估计位姿 $T_k=[R_k|t_k]$ 和地图点 $X_i$ 投影得到的预测像素为：

$${\mathbf{x}}_{i,k}^{proj}=\pi (K[R_k|t_k]X_i)$$

那么重投影误差就是两者的差：

$${\mathbf{e}}_{i,k}={\mathbf{x}}_{i,k}^{obs}-{\mathbf{x}}_{i,k}^{proj}$$

视觉 SLAM 的优化目标，就是最小化所有观测点的重投影误差平方和：

min⁡{Rk,tk,Xi}∑i,kρ⁣(∥ei,k∥2)\min_{\{R_k, t_k, X_i\}} \sum_{i,k} \rho \!\left( \| \mathbf{e}_{i,k} \|^2 \right) {Rk​,tk​,Xi​}min​i,k∑​ρ(∥ei,k​∥2)

其中：

• $\rho (\cdot )$：鲁棒核函数（Huber、Cauchy等）
• 优化变量：相机姿态 $R_k,t_k$ 和地图点 $X_i$

在优化过程中，每一个匹配点都提供一个几何约束：真实图像中的点，预测投影点，之间的偏差越小，说明相机的姿态与地图的几何关系越正确。重投影误差直接反映了整个系统的几何一致性。

延伸：如何使用高斯-牛顿法求解重投影误差

在视觉 SLAM 中，我们的目标是让所有投影到图像上的特征点都尽可能接近它们的真实观测位置。 也就是说，我们要求解一个非线性最小二乘问题：

min⁡{Rk,tk,Xi}∑i,kρ⁣(∥ei,k∥2)\min_{\{R_k, t_k, X_i\}} \sum_{i,k} \rho\!\left(\|\mathbf{e}_{i,k}\|^2\right) {Rk​,tk​,Xi​}min​i,k∑​ρ(∥ei,k​∥2)

其中，重投影误差定义为：
$${\mathbf{e}}_{i,k}={\mathbf{x}}_{i,k}^{obs}-\pi (K[R_k|t_k]X_i)$$
$\pi (\cdot )$ 是投影函数（包含除以 $Z_c$）。

---

重投影误差是非线性的，因为投影涉及：

• 除以 (Z_c)（非线性）；
• 旋转矩阵 (R)（在 SO(3) 上，非线性）。

因此，我们无法直接解析求解，只能线性化近似并迭代优化。 高斯–牛顿法正是处理这类“非线性最小二乘”问题的经典方法。

---

假设我们有 (N) 个残差：
$$E=\frac{1}{2}\sum _{i=1}^N\Vert {\mathbf{e}}_i(\mathbf{x}){\Vert }^2$$

其中 $\mathbf{x}$ 是待优化变量（包括相机姿态、地图点等）。 我们希望找到 $\mathbf{x}$ 使得 $E$最小。

我们在当前估计 $\mathbf{x}$附近做一阶泰勒展开：

$$\mathbf{e}(\mathbf{x}+\Delta \mathbf{x})\approx \mathbf{e}(\mathbf{x})+J\Delta \mathbf{x}$$

其中 $J=\frac{\partial \mathbf{e}}{\partial \mathbf{x}}$是雅可比矩阵。

将线性化残差代入目标函数：

$$E(\mathbf{x}+\Delta \mathbf{x})\approx \frac{1}{2}\Vert \mathbf{e}+J\Delta \mathbf{x}{\Vert }^2$$

对 $\Delta \mathbf{x}$求导并令导数为 0，可得正规方程：

$$(J^{\top }J)\Delta \mathbf{x}=-J^{\top }\mathbf{e}$$

这是高斯–牛顿方程。
我们可以求出：
$$\Delta \mathbf{x}=-(J^{\top }J{)}^{-1}{J}^{\top }\mathbf{e}$$

然后更新参数：
$$\mathbf{x}\leftarrow \mathbf{x}⊞\Delta \mathbf{x}$$
其中 $⊞$表示在李群上的更新操作（例如姿态在 SO(3) 上指数映射更新）。

---

当优化相机位姿 $T=[R|t]$ 时，
我们在线性化时只考虑它的小扰动 $\delta \mathbf{\xi }\in \mathfrak{se}(3)$，
对应一个 6 维向量（3 平移 + 3 旋转）：

$$T^{\prime }=\exp (\delta {\mathbf{\xi }}^{\wedge })T$$

代入重投影函数：
$${\mathbf{e}}_i={\mathbf{x}}_i^{obs}-\pi (KT{X}_i)$$
线性化后：
$${\mathbf{e}}_i(T^{\prime })\approx {\mathbf{e}}_i(T)+J_i\delta \mathbf{\xi }$$
其中 $J_i=\frac{\partial {\mathbf{e}}_i}{\partial \delta \mathbf{\xi }}$是单个特征点关于位姿的雅可比矩阵。

---

对一个点 $P_c=(X_c,Y_c,Z_c)$，其投影为：
$$\{\begin{array}{l}u=f_x\frac{X_c}{Z_c}+c_x\\ v=f_y\frac{Y_c}{Z_c}+c_y\end{array}$$

对相机坐标 $P_c$的偏导为：

$$\frac{\partial (u,v)}{\partial (X_c,Y_c,Z_c)}=\left[\begin{array}{ccc}\frac{f_x}{Z_c}& 0& -\frac{f_x{X}_c}{Z_c^2}\\ 0& \frac{f_y}{Z_c}& -\frac{f_y{Y}_c}{Z_c^2}\end{array}\right]$$

然后再乘以 $P_c$关于姿态扰动$\delta \mathbf{\xi }$ 的偏导：
$$\frac{\partial P_c}{\partial \delta \mathbf{\xi }}=\left[\begin{array}{cc}I& -[P_c{]}_{\times }\end{array}\right]$$

综合得：
$$J_i=\frac{\partial {\mathbf{e}}_i}{\partial \delta \mathbf{\xi }}=-\frac{\partial (u,v)}{\partial (X_c,Y_c,Z_c)}\cdot \frac{\partial P_c}{\partial \delta \mathbf{\xi }}$$

这个 $J_i$ 就是一个 $2\times 6$的雅可比矩阵。

---

高斯–牛顿法适用于误差较小、收敛性较好的情况。
如果误差较大或非线性较强，常使用 Levenberg–Marquardt（LM）法：

$$(H+\lambda I)\Delta \mathbf{x}=b$$

其中 $\lambda$为阻尼因子，用来平衡收敛速度与稳定性。 ORB-SLAM 和 g2o 都在实际中使用了 LM 的形式。