当前位置：首页 > news >正文

力扣2982. 找出出现至少三次的最长特殊子字符串 II

news 2025/10/27 13:42:08

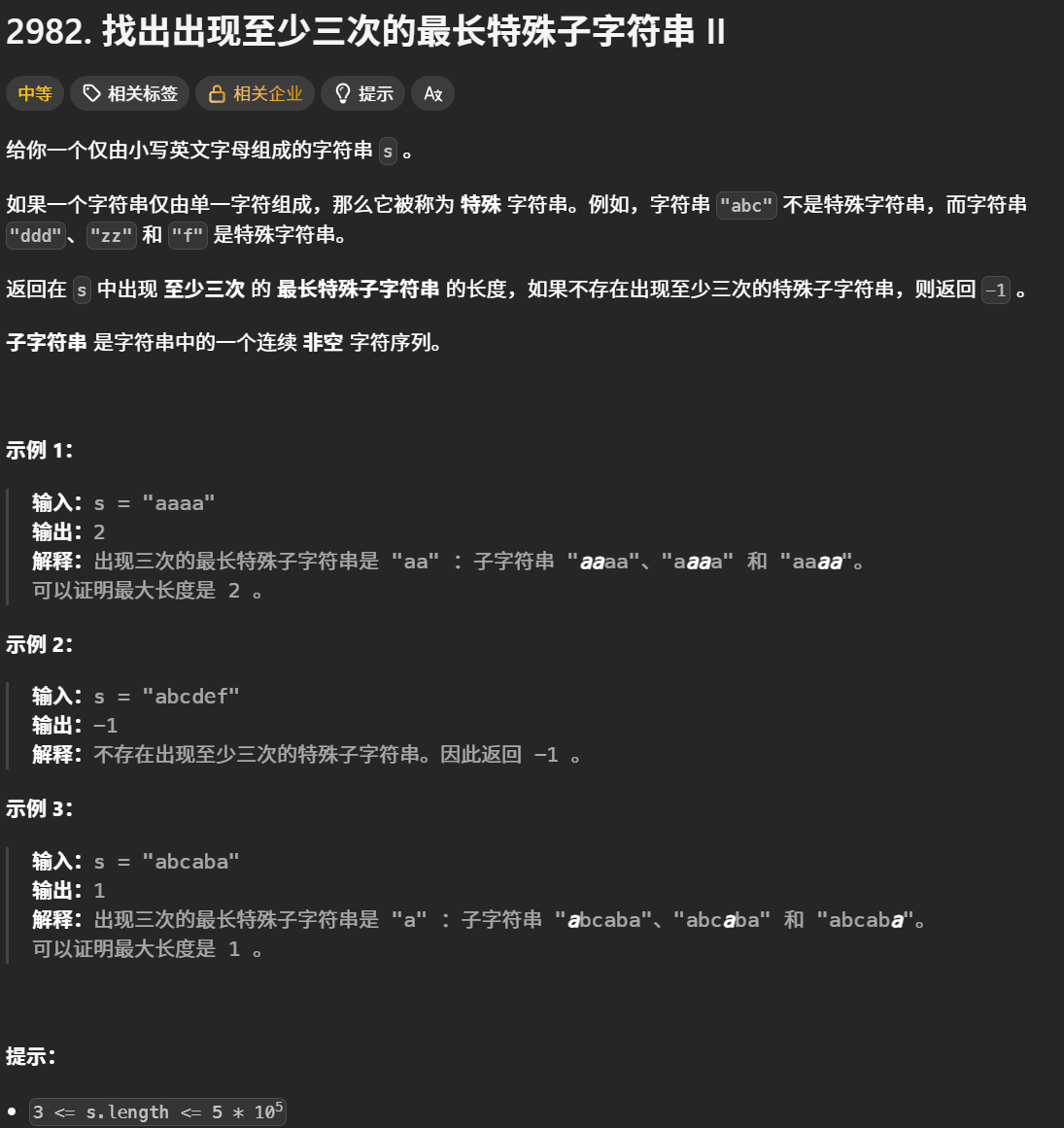
在这里插入图片描述

这一题的大意是给出一个字符串，让末尾找到一种特殊的子串，使得这个子串在给出的大的字符串中出现次数至少3次。那么这个特殊的字符串是什么样的呢，是某一个字符重复出现的，要求这个子字符串尽可能长，也就是说连续字符尽可能的多。
如果用遍历的方法查找一个个枚举子字符串的长度，那么至少是O（n)而再遍历大字符串统计至少出现3次，那么至少是O（n^2)的是一定会超时的。
而枚举子字符串的长度，特别是要找最大值，很明显可以用二分的方式去猜答案。

int l=1;int r=5*100005;int ans=0;while(l<=r){int mid=(l+r)/2;if(check(mid,s)){ans=max(ans,mid);l=mid+1;}else{r=mid-1;}}if(ans==0){return -1;}elsereturn ans;

上面是毫无疑问的，接下来我们只需要写好check函数即可。
那么就相当于已知子字符串的长度x，让我们在大字符串中寻找是否有符合长度的子字符串。
我想到的是从’a’到‘z’一个一个去遍历，看在字符串中是否有长度为x的从‘a’到’z’的字符。
从大字符串中截取相同长度的子字符串然后与给出的比较，如果相同则次数++。

 bool check(int x,string& s){if(x>s.size()){return false;}for(int i=0;i<26;i++){string temp(x,'a'+i);int t=-1;int cnt=0;for(int j=0;j<s.size()-x+1;j++){if(temp==s.substr(j,x)){cnt++;}if(cnt>=3){return true;}}}return false;}

这样虽然符合题意，但时间复杂度过于大O(logn） * 26 * O（n)*O(x)
这里的x可能过于大导致超时。
我们可以选择用哈希表来存储每一个字符，然后采用双指针的方式，如果这个字符在大的字符串中连续出现超过了x次，那么我们就可以计算出这个由这个连续出现的子串，会构成 j-i-x+1个符合长度为x的特殊子字符串。
如果某一个字符的出现次数超过3就符合题意，反之不符合题意。

class Solution {
public:bool check(int x,string& s){if(x>s.size()){return false;}unordered_map<char,int> mp;int i=0;while(i<s.size()){int j=i+1;while(j<s.size()&&s[j]==s[i]){j++;}if(j-i>=x)mp[s[i]]+=j-i-x+1;if(mp[s[i]]>=3){return true;}i=j;}return false;}int maximumLength(string s) {int l=1;int r=5*100005;int ans=0;while(l<=r){int mid=(l+r)/2;if(check(mid,s)){ans=max(ans,mid);l=mid+1;}else{r=mid-1;}}if(ans==0){return -1;}elsereturn ans;}
};