实验一:基于MATLAB控制系统单位阶跃响应分析
前言
二阶系统的闭环极点分布及其阶跃响应的特点
值 闭环极点分布的特点 阶跃响应的特点
ζ< 0 两个正实部的特征根, 振荡发散的曲线
位于s右半平面
ζ= 0 一对共轭纯虚根, 等幅振荡曲线
无阻尼系统 位于s平面虚轴上
0 < ζ < 1 两个负实部的共轭复根, 衰减振荡曲线
欠阻尼系统 位于s左半平面
ζ = 1 两个相等的负实根, 单调上升收敛的曲线
临界阻尼系统 位于s左半平面实轴
ζ>1 两个不相等的负实根, 上升速度较时慢
过阻尼系统 s的左半平面实轴
1. 实验内容
已知二阶控制系统:

求系统的单位阶跃响应
step ( ) 函数可以计算连续系统单位阶跃响应,其调用格式为:
step (sys) 或step ( sys , t ) 或step (num , den)
函数在当前图形窗口中直接绘制出系统的单位阶跃响应曲线,对象sys可以由tf ( ),zpk ( ) 函数中任何一个建立的系统模型。第二种格式中t可以指定一个仿真终止时间,也可以设置为一个时间矢量(如t=0 : dt : Tfinal,即dt是步长,Tfinal是终止时刻)。
(1)当ε =0,0.25,0.5,0.75,1,1.25时,求对应系统的闭环极点、自然振荡频率及阶跃响应曲线。
(2)当wn=10,30,50时,求系统的阶跃响应曲线。
实验代码
当ε =0,0.25,0.5,0.75,1,1.25时,求对应系统的闭环极点、自然振荡频率及阶跃响应曲线。
num =100 ; i = 0 ;
for sigma = 0 : 0.25 : 1.25
den = [1 2sigma10 100] ;
damp (den)
sys = tf (num , den) ;
i = i+1 ;
step (sys , 2)
hold on
end
grid
hold off
title ( ‘阻尼比不同时的阶跃响应曲线’ )
lab1= ‘ζ = 0’; text (0.3, 1.9, lab1),
lab2 = ‘ζ = 0.25’; text (0.3, 1.5, lab2),
lab3 = ‘ζ= 0.5’; text (0.3, 1.2, lab3),
lab4 = ‘ζ=0.75’; text (0.3, 1.05, lab4),
lab5 = ‘ζ=1’; text (0.35, 0.9, lab5),
lab6 = ‘ζ=1.25’; text (0.35, 0.8, lab6)
实验结果

分析
可见当wn一定时,系统随着阻尼比的增大,闭环极点的实部在s左半平面的位置更加远离原点,虚部减小到0,超调量减小,调节时间缩短,稳定性更好。
实验代码
当wn=10,30,50时,求系统的阶跃响应曲线
sgma = 0.25 ; i=0 ;
for wn =10 : 20 : 50
num = wn ^2 ; den = [1, 2sgmawn , wn ^2] ;
sys = tf (num , den) ;
i=i+1 ;
step (sys , 2)
hold on , grid
end
hold off
title (’ wn 变化时系统的阶跃响应曲线’)
lab1 = ‘wn = 10’ ; text (0.35, 1.4, lab1),
lab2 = ‘wn = 30’ ; text (0.12, 1.3, lab2),
lab3 = ‘wn = 50’; text (0.05, 1.2, lab3)
实验结果
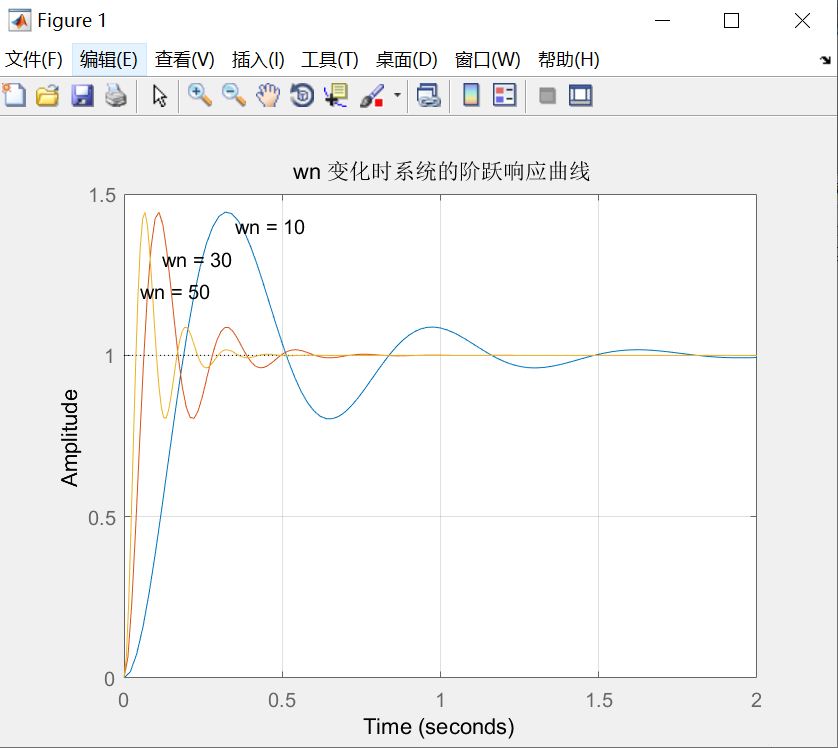
分析
可见,当ε一定时,随着wn增大,系统响应加速,振荡频率增大,系统调整时间缩短,但是超调量没变化
