将有序数组转换为二叉搜索树-力扣

一、核心思路

利用升序数组的特性和平衡二叉搜索树的定义，通过递归分割数组构建树：

选择数组的中间元素作为根节点（确保左右子树节点数量均衡）；

左半部分数组递归构建左子树（所有元素小于根节点，满足 BST 左小右大特性）；

右半部分数组递归构建右子树（所有元素大于根节点）；

重复以上步骤，直至数组为空（递归终止）。

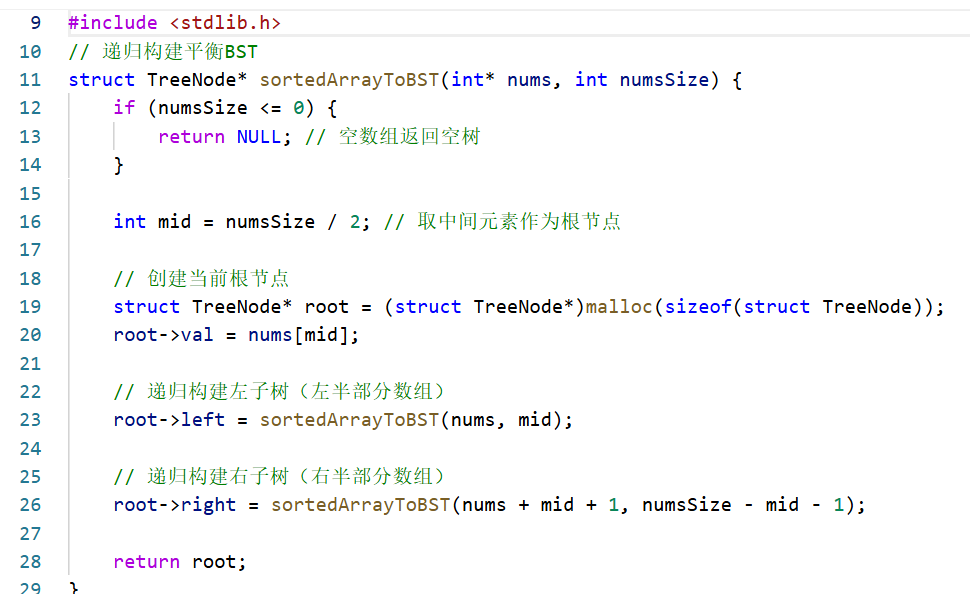
二、原理

二叉搜索树（BST）特性：对任意节点，左子树所有节点值 < 节点值 < 右子树所有节点值。升序数组的左半部分元素天然小于中间元素，右半部分元素天然大于中间元素，因此分割后自然满足 BST 的数值关系。

平衡树特性：左右子树的高度差不超过 1。每次选择中间元素作为根节点，可保证左、右子树的节点数量最多相差 1（数组长度为奇数时相等，偶数时差 1），递归构建后左右子树高度差必然≤1，从而满足平衡条件。

三、优点

简单直观：直接利用数组有序性和递归思想，逻辑清晰，代码简洁。

高效性：

时间复杂度：O (n)，每个元素仅需一次访问（创建节点）；

空间复杂度：O (log n)，递归栈深度等于树的高度（平衡树高度为 log n，n 为数组长度）。

天然平衡：通过中间元素分割数组，无需额外调整平衡（如 AVL 树的旋转操作），从构建过程就保证了平衡性。

普适性：对任意升序数组均有效，且可生成多种合法平衡 BST（如偶数长度数组可选择中间左 / 右元素作为根）。

总结

该方法的核心是中间元素为根，递归分割数组，既利用了升序数组的有序性满足 BST 的数值关系，又通过均衡分割保证了树的平衡性，是一种高效、简洁的构建方式。