线性dp合集

最长递增子序列

 

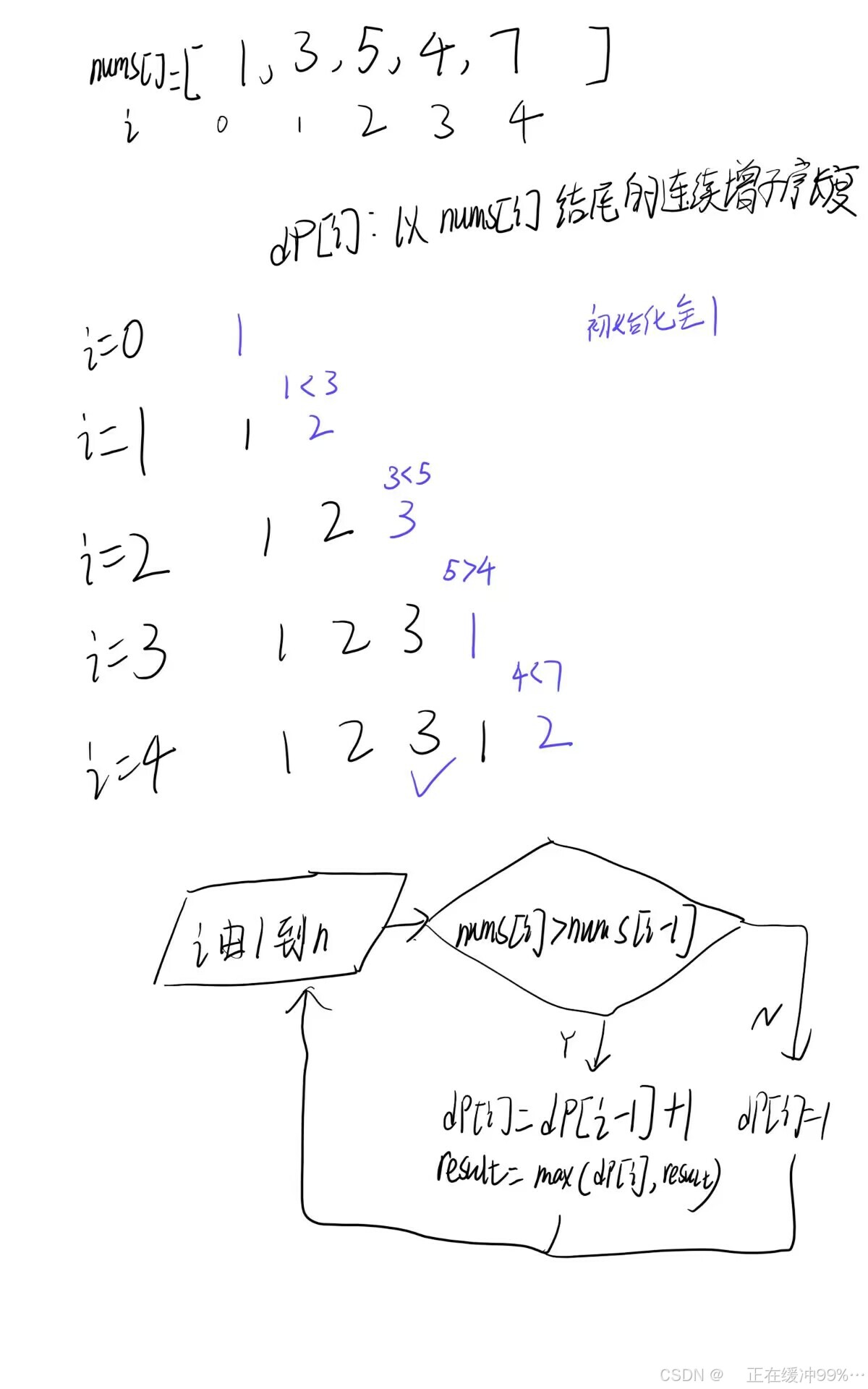
 dp[i]表示以nums[i]这个数结尾的时的严格递增子序列的最长长度，那么只要每次增加一个数字nums[i]并且这个nums[i]比之前的nums[j]要大，dp[i]就要更新为dp[i]和dp[j]+1二者的最大值，初始化默认最大递增子序列都是1

这里遍历顺序的感觉很像完全背包，每次增加一个物品nums[i]，然后对原本的最大子序列再进一步判断，只要增加的nums[i]比之前的子序列最后一个数字要大，那么就拼接上更新最大子序列长度

 错误代码：这里我忘记了dp[i]的含义，最后结果dp[n-1]存储的是以nums[n-1]结尾的子序列的最大递增长度，在这个错误案例中，正确的子序列是[1,3,6,7,9,10]，而我的错误代码得到的子序列是[1,3,4,5,6]

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n =nums.size();vector<int> dp(n,1);for(int i=1;i<n;i++)for(int j=0;j<i;j++)if(nums[i]>nums[j])dp[i]=max(dp[i],dp[j]+1);return dp[n-1];}
};

 正确代码：应该用一个结果存储真正的最长递增子序列也就是dp[n-3]而不是dp[n-1]的值

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n =nums.size();int result=1;vector<int> dp(n,1);for(int i=1;i<n;i++){for(int j=0;j<i;j++)if(nums[i]>nums[j])dp[i]=max(dp[i],dp[j]+1);result=max(result,dp[i]);}return result;}
};

java版本

class Solution {public int lengthOfLIS(int[] nums) {int result = 1;int n = nums.length;int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}result = Math.max(dp[i], result);}return result;}
}

最长连续递增序列

 

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {int n =nums.size();vector<int> dp(n);dp[0]=1;int result=1;for(int i=1;i<n;i++){if(nums[i-1]<nums[i]){dp[i]=dp[i-1]+1;result=max(dp[i],result);}elsedp[i]=1;}return result;}
};

最长重复子数组

 

 二维空间版

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size(),n=nums2.size();vector<vector<int>> dp(m,vector<int>(n));int result=0;for(int i=0;i<m;i++)if(nums1[i]==nums2[0]){dp[i][0]=1;result=1;}for(int j=0;j<n;j++)if(nums1[0]==nums2[j]){dp[0][j]=1;result=1;}for(int i=1;i<m;i++)for(int j=1;j<n;j++){if(nums1[i]==nums2[j]){dp[i][j]=dp[i-1][j-1]+1;result=max(result,dp[i][j]);}}return result;}
};

 一维滚动数组版，跟01背包的滚动数组一样由于内层循环需要由后向前遍历，因为dp[j]=dp[j-1]+1中这个dp[j-1]是上一层的数据如果由前向后遍历会覆盖掉导致dp[j]加错值

class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size(),n=nums2.size();vector<int> dp(n);int result=0;for(int i=0;i<m;i++){// 由于j-1的存在将j=0的情况剥离出去单独判断for(int j=n-1;j>=1;j--){if(nums1[i]==nums2[j]){dp[j]=dp[j-1]+1;result=max(dp[j],result);}elsedp[j]=0;}if(nums1[i]==nums2[0]){dp[0]=1;result==max(dp[0],result);}elsedp[0]=0;}return result;}
};

优化版本

二维代码

class Solution {public int findLength(int[] nums1, int[] nums2) {int result=0;int[][] dp=new int[nums1.length+1][nums2.length+1];for(int i=1;i<=nums1.length;i++){for(int j=1;j<=nums2.length;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=0;}result=Math.max(result,dp[i][j]);}}return result;}
}

一维代码

class Solution {public int findLength(int[] nums1, int[] nums2) {int result=0;int[] dp=new int[nums2.length+1];for(int i=1;i<=nums1.length;i++){for(int j=nums2.length;j>=1;j--){if(nums1[i-1]==nums2[j-1])dp[j]=dp[j-1]+1;elsedp[j]=0;result=Math.max(result,dp[j]);}}return result;}
}

最长公共子序列

 

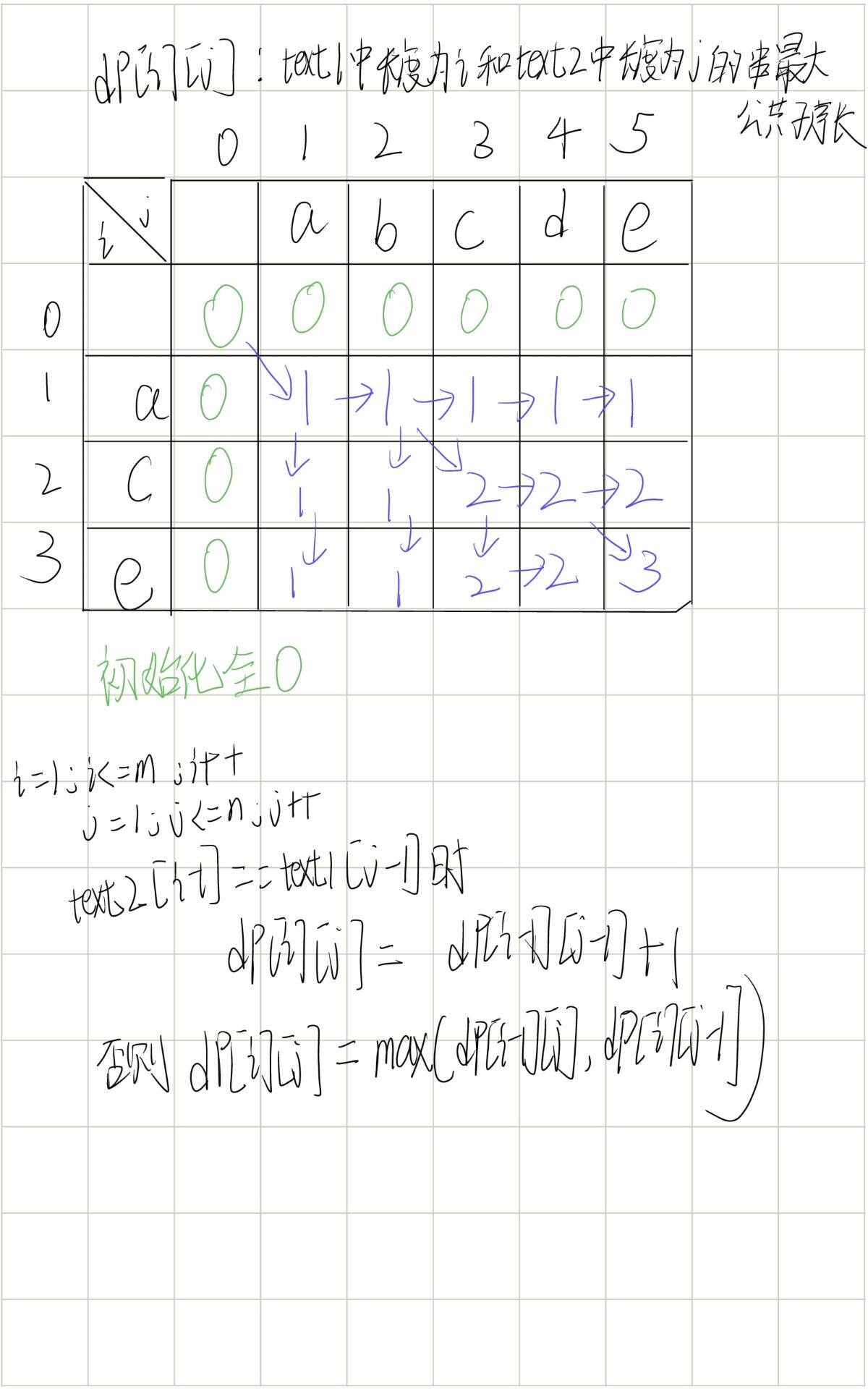
这道题目和最长重复子数组是一个类型的不同之处在于text1[i]!=text2[j]时dp[i][j]时他的值是继承上一行或上一列的最大值，二者dp数组的含义也不一样，这里的dp[i][j]表示的是以text[i]和text2[j]为结尾的子序列最大长度，这也是导致两种问题当判断不等的时候处理逻辑不同，对于子数组由于不能跨元素作为子数组所以不等的时候只能赋值为0，而子序列是可以跨元素的所以不等时是可以继承自上一行和上一列

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int m=text1.size(),n=text2.size();vector<vector<int>> dp(m,vector<int>(n));//默认全0dp[0][0]=text1[0]==text2[0]?1:0;for(int j=1;j<n;j++){if(text1[0]==text2[j])dp[0][j]=1;elsedp[0][j]=dp[0][j-1];}for(int i=1;i<m;i++){// j为0的情况单独判断if(text1[i]==text2[0])dp[i][0]=1;elsedp[i][0]=dp[i-1][0];for(int j=1;j<n;j++){if(text1[i]==text2[j])dp[i][j]=dp[i-1][j-1]+1;elsedp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[m-1][n-1];}
};

臃肿代码改进：

java版本代码：

class Solution {public int longestCommonSubsequence(String text1, String text2) {int m = text1.length();int n = text2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (text1.charAt(i - 1) == text2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);} }}return dp[m][n];}
}

不相交的线

 

 这道题看起来可能没有思路，但是实际上仔细观察会发现将相等的数字连接起来，并且不相交，就相当于是元素的原有相对顺序不变求其最大子序和，那么这道题目就是最长公共子序列，代码一模一样

class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp=new int[nums1.length+1][nums2.length+1];for(int i=1;i<=nums1.length;i++){for(int j=1;j<=nums2.length;j++){if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;elsedp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);}}return dp[nums1.length][nums2.length];}
}

不同的子序列

 

 依旧是动态规划的子序列问题，这里要注意的是对于s[i]==t[j]的时候执行的逻辑与以往不同，二者相等的时候意味着方案数增多。新方案是以i-1为结尾和以j-1为结尾的方案数，因为相等的时候意味着我们拿s[i]去匹配t[j]，s的前i-1去匹配t的前j-1；旧方案是i-1，j时的方案也就是我们不用s[i]和t[j]去匹配的方案数目，二者求和就是dp[i][j]。如果不相等就继承原有的方案数目。

class Solution {
public:int numDistinct(string s, string t) {int m=s.size(),n=t.size();vector<vector<int>> dp(m,vector<int>(n));dp[0][0]=s[0]==t[0]?1:0;for(int i=1;i<m;i++){if(s[i]==t[0])dp[i][0]=dp[i-1][0]+1;elsedp[i][0]=dp[i-1][0];for(int j=1;j<n;j++){if(s[i]==t[j]){if(dp[i-1][j-1]<INT_MAX-dp[i-1][j])dp[i][j]=dp[i-1][j-1]+dp[i-1][j];}elsedp[i][j]=dp[i-1][j];}}return dp[m-1][n-1];}
};

一维滚动数组版 

class Solution {
public:int numDistinct(string s, string t) {int m=s.size(),n=t.size();vector<int> dp(n);dp[0]=s[0]==t[0]?1:0;for(int i=1;i<m;i++){for(int j=n-1;j>0;j--)if(s[i]==t[j])if(dp[j-1]<INT_MAX-dp[j])dp[j]=dp[j-1]+dp[j];if(s[i]==t[0])dp[0]=dp[0]+1;}return dp[n-1];}
};

dp的另一种思路（代码简化版本）

class Solution {public int numDistinct(String s, String t) {int m = s.length();int n = t.length();int[][] dp = new int[m + 1][n + 1];for(int i=0;i<=m;i++)dp[i][0]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n&&j<=i/*j<=n是防止数组越界，j<=i是下三角遍历*/;j++){if (s.charAt(i - 1) == t.charAt(j - 1)) {dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];} else {dp[i][j] = dp[i - 1][j];} }}return dp[m][n];}
}

class Solution {public int numDistinct(String s, String t) {int m = s.length();int n = t.length();int[] dp = new int[n + 1];dp[0] = 1;for(int i=1;i<=m;i++){for (int j = Math.min(i, n); j >= 1; j--) {if (s.charAt(i - 1) == t.charAt(j - 1)) {dp[j] += dp[j - 1];}}}return dp[n];}
}

编辑距离

 

 一开始以为还是最大公共子序列问题，求出最大公共子序列后用word1的长度减去最大公共子序列的长度就可以解决问题了，结果示例2中最大公共子序列为etion，得到的结果为4，无法解决这道题

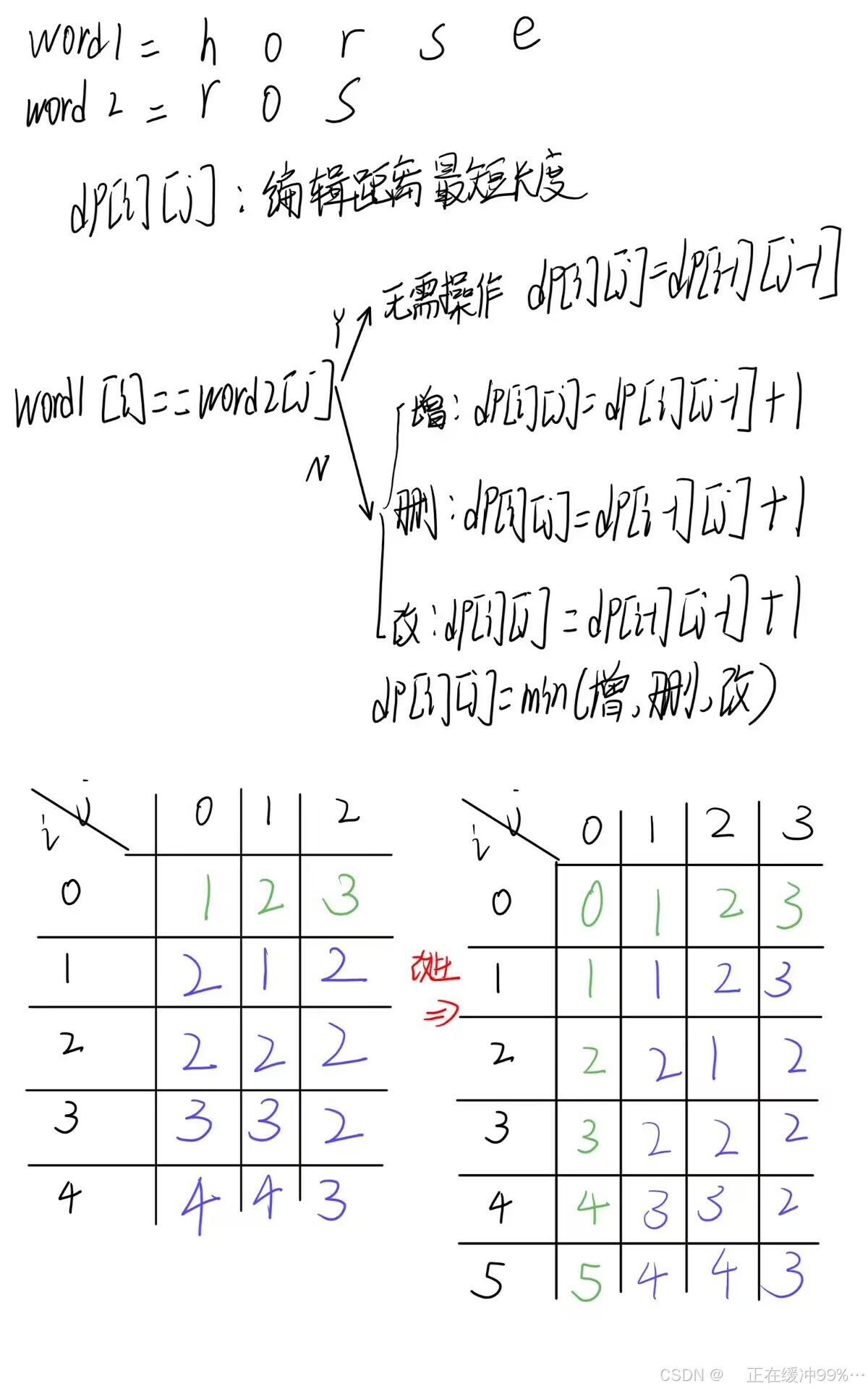
那就按部就班得进行动态规划分析，设置dp[i][j]为以word1中以i结尾的串和word2中以j结尾的串编辑距离的最小值，那么在word1[i]和word2[j]相等时就应该直接继承i-1和j-1的情况，而不相等时就取增删改的最小值，依据状态依赖关系遍历顺序应该是内外层都从前向后遍历，具体情况可看下图

 

class Solution {
public:int minDistance(string word1, string word2) {int m=word1.size(),n=word2.size();if(m==0)return n;if(n==0)return m;vector<vector<int>> dp(m,vector<int>(n));dp[0][0]=word1[0]==word2[0]?0:1;for(int j=1;j<n;j++){if(word1[0]==word2[j])dp[0][j]=dp[0][j-1];elsedp[0][j]=dp[0][j-1]+1;}for(int i=1;i<m;i++){if(word1[i]==word2[0])dp[i][0]=dp[i-1][0];elsedp[i][0]=dp[i-1][0]+1;for(int j=1;j<n;j++){if(word1[i]==word2[j])dp[i][j]=dp[i-1][j-1];elsedp[i][j]=min({dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1});}}return dp[m-1][n-1];}
};

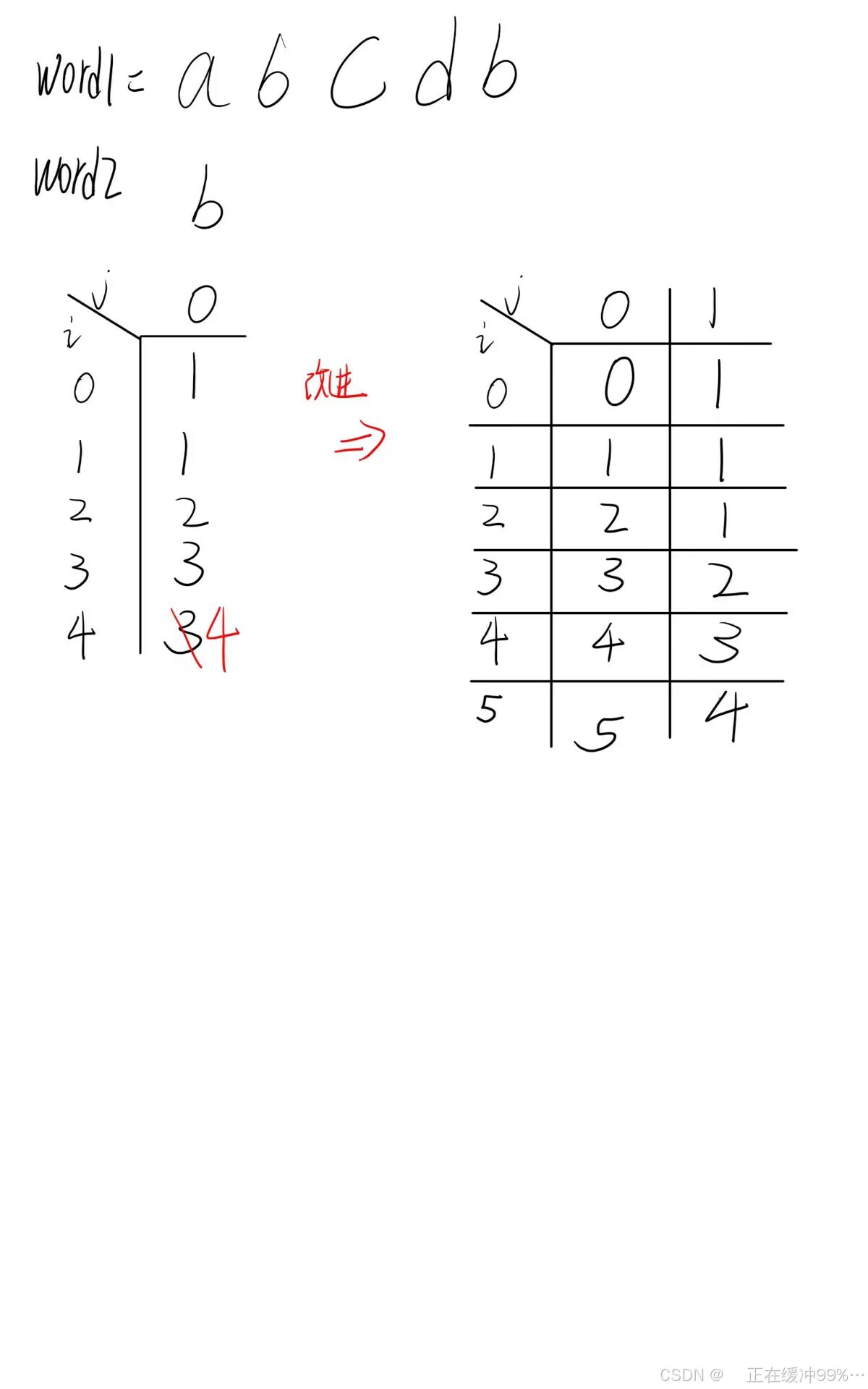
 分析完后把如上代码一提交结果不通过，仔细分析发现对于如下这种边界的特殊情况没有考虑到，两次出现b相等的情况应该是只有一次是dp[0][j]=dp[0][j-1]，第二次以及之后都是dp[0][j]=dp[0][j-1]+1，所以要额外判断是否是第一次出现相等的情况，所以引入一个标识flag来判别

 

class Solution {
public:int minDistance(string word1, string word2) {int m=word1.size(),n=word2.size();if(m==0)return n;if(n==0)return m;vector<vector<int>> dp(m,vector<int>(n));dp[0][0]=word1[0]==word2[0]?0:1;for(int j=1;j<n;j++){if(word1[0]==word2[j])dp[0][j]=dp[0][j-1];elsedp[0][j]=dp[0][j-1]+1;}bool flag=false;for(int i=1;i<m;i++){if(word1[i]==word2[0]&&!flag){dp[i][0]=dp[i-1][0];flag=true;}elsedp[i][0]=dp[i-1][0]+1;for(int j=1;j<n;j++){if(word1[i]==word2[j])dp[i][j]=dp[i-1][j-1];elsedp[i][j]=min({dp[i][j-1]+1,dp[i-1][j]+1,dp[i-1][j-1]+1});}}return dp[m-1][n-1];}
};

 如上代码就是引入了flag的代码，可以ac了，但是感觉这样写就是一坨屎，特殊情况代码太多，核心没有体现，可阅读性不高，所以调整一下干脆扩充一下dp数组用再多添加一行一列来进行辅助，这时候dp[i][j]的含义是word1中长度为i的串修改到word2中长度为j的串最小的操作数，最后得到改进的代码如下，正好多扩充的一行一列相当于判断了空串的情况

class Solution {
public:int minDistance(string word1, string word2) {int m=word1.size(),n=word2.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=m;i++)dp[i][0]=dp[i-1][0]+1;for(int j=1;j<=n;j++)dp[0][j]=dp[0][j-1]+1;for(int i=1;i<=m;i++)for(int j=1;j<=n;j++){if(word1[i-1]==word2[j-1])dp[i][j]=dp[i-1][j-1];elsedp[i][j]=min({dp[i][j-1],dp[i-1][j],dp[i-1][j-1]})+1;}return dp[m][n];}
};

java版本

class Solution {public int minDistance(String word1, String word2) {int m = word1.length();int n = word2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 0; i <= m; i++) {dp[i][0] = i;}for (int j = 0; j <= n; j++) {dp[0][j] = j;}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {dp[i][j] = Math.min(dp[i][j - 1], Math.min(dp[i - 1][j], dp[i - 1][j - 1])) + 1;} }}return dp[m][n];}
}