强化学习推荐系统：不同的探索策略——贪心探索策略（4.1）

阅读《强化学习与大模型推荐系统》应具备一定的深度学习和推荐系统技术基础，适合于对大模型和强化学习推荐技术感兴趣的读者学习参考。
《强化学习与大模型推荐系统》全书下载地址：https://github.com/ByShui/Book_RL-LLM-In-RS。

强化学习推荐系统：不同的探索策略——贪心探索策略（4.1）

一个优秀的探索策略要能够同时满足探索和利用的需求，以下代码构造了一个具有5个动作的策略评估环境，以此来对不同探索策略的累计遗憾值进行分析：

class Bandit:def __init__(self, arm_count):self.arm_count = arm_countself.generate_arms()def generate_arms(self):self.arms = []for _ in range(self.arm_count):mean = np.random.normal(0, 1)std_dev = np.random.uniform(0.5, 1.5)self.arms.append((mean, std_dev))def reward(self, arm):mean, std_dev = self.arms[arm]return np.random.normal(mean, std_dev)def optimal_arm(self):return np.argmax([mean for mean, _ in self.arms])if __name__ == "__main__":arm_count = 5bandit = Bandit(arm_count)

具体来说，策略评估环境中设置了5个臂，摇动臂的奖励${\text{reward}}_a$服从不同的正态分布：$${\text{reward}}_a=\mathcal{N}(\mu ,\sigma )$$其中，$\mu$和$\sigma$分别是正态分布的均值和方差，它们是随机生成的。定义拥有最大均值的动作是最优动作$a_{\ast }$，最优价值$V_{\ast }$从最优臂的价值分布中采样得到。

优化策略需要牺牲短期利益，因为需要通过探索搜集更多的信息以获得更优的动作，使得智能体最终能够获得更多回报。探索和利用是强化学习中的一对矛盾体，这意味着在学习过程中，智能体需要在已知和未知的情况下做出最优的决策。

其中，利用是指在已知情况下选择已知最优的策略来获得收益，而探索是指在未知情况下，为了获取更多的信息和收益，选择不同的策略进行尝试。

探索是指在不确定性的环境中，探索新的策略或动作来获得更高的奖励或效用，包含两个部分：一是尝试未知的行为，以期找到更好的策略并更新模型；二是平衡已知和未知的行为，以确保不会错过可能的好策略。

在推荐系统中，探索可以包括推荐新的项目、向用户提供个性化的推荐建议或者探索不同的推荐策略（如多臂机）。探索和利用需要平衡，以确保推荐系统具有长期的优化效果。

一个标准的强化学习算法包括探索和利用两个步骤——探索帮助智能体充分了解其状态空间，利用则帮助智能体找到最优的动作序列。

用来平衡探索和利用的方法包括：贪心探索策略、高斯探索策略、UCB探索策略、玻尔兹曼探索策略、汤普森采样探索策略和熵正则化探索策略等，本篇博客我们介绍一下贪心探索策略。

1. 贪心探索策略

MAB中的贪心策略指对贪心策略添加噪声的策略，如$ϵ$-贪心策略、衰减${ϵ}_t$-贪心策略。

（1）$ϵ$-贪心策略。 原始的贪心策略每次只选择已知的最优动作，这导致探索不足，有可能锁死在一个次优的动作上。$ϵ$-贪心策略设定了一个固定的探索率$ϵ\in [0,1]$，让智能体在每次选择动作时以$ϵ$的概率选择其他动作（探索），以$1-ϵ$的概率选择当前的最优动作（利用）：$$a_t=\{\begin{array}{ll}{\mathrm{argmax}}_{a\in A}{Q}_t(a)& P(1-ϵ)\\ \text{otherwise}& P(ϵ)\end{array}$$

如下代码实现了$ϵ$-贪心策略：

def epsilon_greedy(bandit, T, epsilon):arm_count = bandit.arm_countQ = np.zeros(arm_count)N = np.zeros(arm_count)cumulative_regret = [0]for t in range(1, T+1):if np.random.rand() < epsilon:arm = np.random.randint(arm_count)else:arm = np.argmax(Q)reward = bandit.reward(arm)N[arm] += 1Q[arm] += (reward - Q[arm]) / N[arm]optimal_reward = bandit.reward(bandit.optimal_arm())cumulative_regret.append(cumulative_regret[-1] + (optimal_reward - reward))return cumulative_regretif __name__ == "__main__":arm_count = 5T = 1000bandit = Bandit(arm_count)cumulative_regret_epsilon_greedy = epsilon_greedy(bandit, T, epsilon=0.1)

以上代码定义了epsilon_greedy()方法，它接收3个参数：

• bandit（一个多臂机实例）；
• T（试验轮次，即在多臂机上探索/利用的轮次）；
• epsilon（探索率，取值范围为0~1，它是一个用于平衡探索与利用的超参数）。

数组Q和N分别用于存储每个臂的平均奖励和被摇动的次数。随后执行T轮试验，在每轮试验中，智能体以epsilon的概率进行探索，以1-epsilon的概率进行利用。每轮试验结束后，更新所选臂的被摇动的次数和平均奖励，其中，平均奖励是通过一种常见的增量平均方法来计算的。最后计算累计遗憾值，将其添加到累计遗憾列表中，在这个过程中，最优臂是已知的，但最优价值依然从最优臂的价值分布中采样得到。

（1）衰减${ϵ}_t$-贪心策略。 尽管$ϵ$-贪心策略兼顾了探索与利用，但它永远无法收敛到最优解，因为它总按照一个的固定概率执行探索，不能每次都利用最优动作。衰减${ϵ}_t$-贪心策略就是为了解决这个问题而产生的。

设动作$a$的价值与最优价值的差值为：$${\Delta }_a=V_{\ast }-Q_t(a)$$

则当前的最优动作的价值与最优价值之间的差值可以表示为：$$d=\underset{{\Delta }_a\in A}{\min }{\Delta }_a$$

那么，当前时间步的探索率就可以表示为：ϵt=min⁡{1,c∣A∣d2t}\epsilon_t=\min\{1,\frac{c|A|}{d^2t}\}ϵt​=min{1,d2tc∣A∣​}其中，$c$是权重超参数，$|A|$是臂的数量，即项目的数量。

得到探索率${ϵ}_t$后，就可以利用$ϵ$-贪心策略的公式进行动作选择了。探索率${ϵ}_t$会随着时间以$1/t$的速率减小，遗憾值呈现与时间步的对数关系，即$${\int }_0^{\infty }(1/t)\text{d}t=\ln |t|$$这意味着该探索策略将会收敛地很快，这个收敛速度主要受差值$d$影响，在实践中还有两种设置方法：

• 设置为一个超参数，由人工手动调参；
• 设置为最优动作与次优动作之间的价值差。这种设置方法来源于这样一个思想，最优动作与次优动作之间的价值差距越大，表示最优策略更容易区分，此时 应当衰减得更快，以便更多地选择最优动作；反之，如果差距较小就表示最优策略不容易区分，此时探索率应当衰减得慢一些，以便增加探索的机会。

如下代码实现了衰减${ϵ}_t$-贪心策略：

def decay_epsilon_greedy(bandit, T, c=0.1):arm_count = bandit.arm_countQ = np.zeros(arm_count)N = np.zeros(arm_count)cumulative_regret = [0]for t in range(1, T+1):d = min(bandit.reward(bandit.optimal_arm()) - Q)epsilon_t = min(1, c * arm_count / (d**2 * (t + 1)))if np.random.rand() < epsilon_t:arm = np.random.randint(arm_count)else:arm = np.argmax(Q)reward = bandit.reward(arm)N[arm] += 1Q[arm] += (reward - Q[arm]) / N[arm]optimal_reward = bandit.reward(bandit.optimal_arm())cumulative_regret.append(cumulative_regret[-1] + (optimal_reward - reward))return cumulative_regretif __name__ == "__main__":arm_count = 5T = 1000bandit = Bandit(arm_count)cumulative_regret_decay_epsilon_greedy = decay_epsilon_greedy(bandit, T, c=0.1)

以上代码定义了decay_epsilon_greedy()方法，它接收三个参数：

• bandit，一个多臂机实例；
• T，试验轮次，即在多臂机上探索/利用多少轮；
• c，超参数，用于调整衰减速度。较大的c值将导致衰减速度降低，从而增加探索的可能性；较小的c值将导致衰减速度加快，减少探索的可能性。

我们在每轮试验中根据当前时间步的探索率${ϵ}_t$计算当前的衰减探索率 ，并执行${ϵ}_t$-贪心策略。

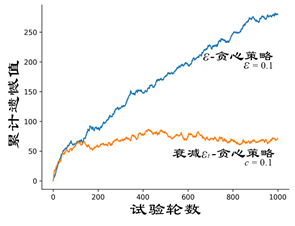
为了更好地观察两种探索策略的效果，上面的图分别绘制了$ϵ$-贪心策略和衰减${ϵ}_t$-贪心策略试验1000轮次后的累计遗憾值曲线，从图中可以看出两种探索策略在50轮左右的累计遗憾值变化幅度放缓，这说明它们此时都找到了最优臂。但是，$ϵ$-贪心策略的累计遗憾值依然在不断增长，这是因为它总是保持了一定的探索几率。相比之下，衰减${ϵ}_t$-贪心策略的累计遗憾值在200轮左右就达到了收敛状态，此后仅在小范围内波动，这是因为探索率${ϵ}_t$快速衰减，从200轮左右开始就不再执行探索。