对于使用队列实现栈以及用栈实现队列的题目的解析
开篇介绍:
hello 大家,是我是我又是我~那么在前面两篇博客中,我们了解并实践了栈和队列这两个数据结构类型,我们也知道,栈的特点是后进先出,队列的特点是先进先出,那么不知道大家好不好奇,我们能分别用顺序表实现栈,用单向链表实现队列,那么,我们能不能用队列实现栈,用栈实现队列呢?
答案是可以的,但是其实说实话,这个压根没什么用,队列就队列,栈就栈,为什么要用队列实现栈,用栈实现队列呢? 简直是多此一举,确实是多此一举,但是呢,它们也有它们的意义存在,所谓存在即合理。
我们可以利用这两个题目,去大大加深我们对栈和队列的理解,帮助我们更进一步的熟记以及运用这两个数据结构,那么,这两道题目的存在,就有意义了,即使它们我们未来用不到。
那么接下来,就让我带着大家,一起将这两道题解决吧。
依旧是老规矩,我先给上这两个题目的链接,大家先自行练练手。
225. 用队列实现栈 - 力扣(LeetCode)![]() https://leetcode.cn/problems/implement-stack-using-queues/232. 用栈实现队列 - 力扣(LeetCode)
https://leetcode.cn/problems/implement-stack-using-queues/232. 用栈实现队列 - 力扣(LeetCode)![]() https://leetcode.cn/problems/implement-queue-using-stacks/description/
https://leetcode.cn/problems/implement-queue-using-stacks/description/
225. 用队列实现栈:
这道题的难度是不大的,我们先看题目:
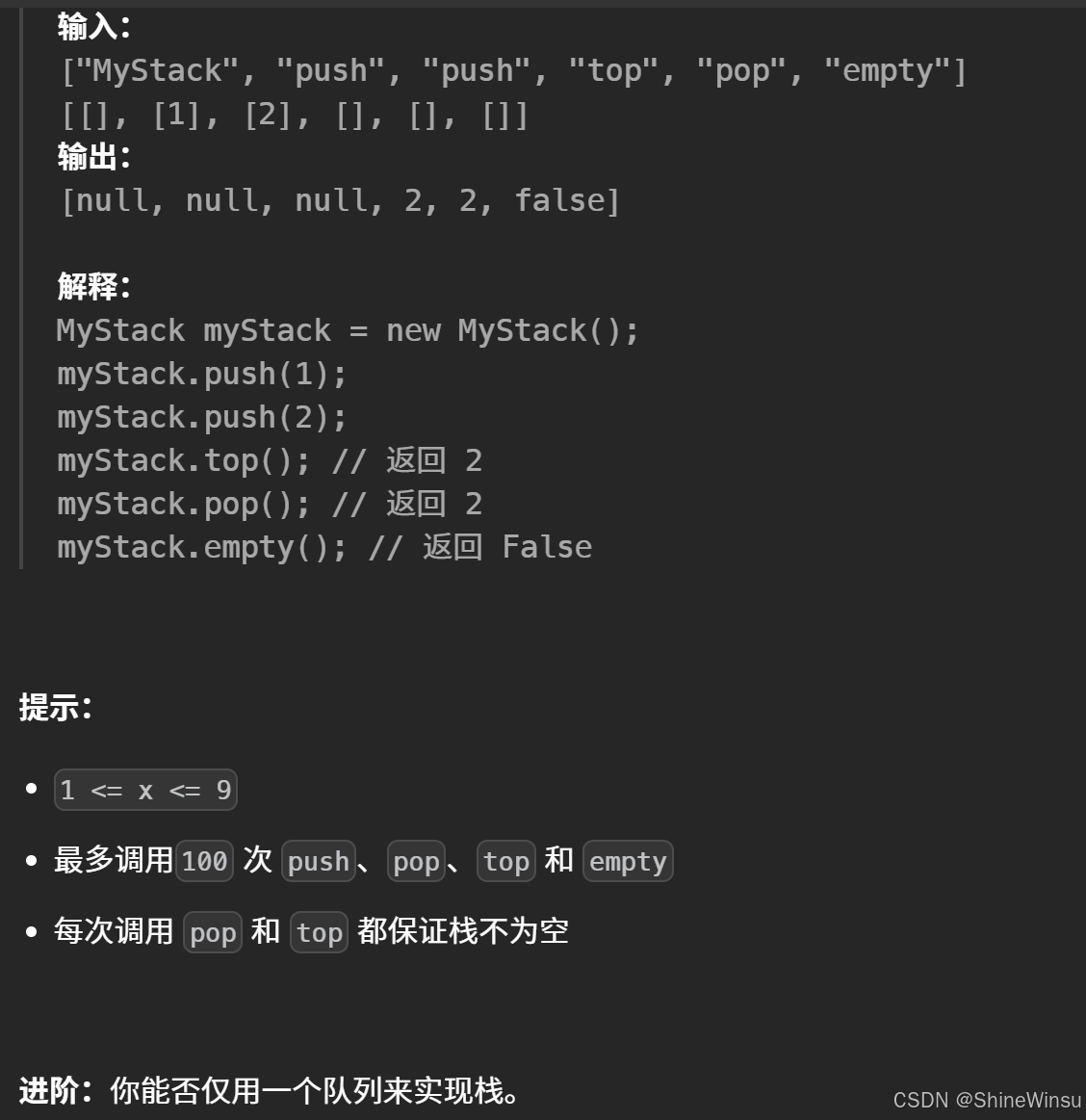
题意分析:
这道题要求仅使用两个队列来实现一个 ** 后进先出(LIFO)** 的栈,并支持栈的四种基本操作:push(压入栈顶)、pop(移除并返回栈顶元素)、top(返回栈顶元素)、empty(判断栈是否为空)。
关键限制
- 只能使用队列的标准操作,即
push to back(队尾入队)、peek/pop from front(队头查看 / 出队)、size(队列大小)、is empty(队列是否为空)。 - 如果所用语言不支持队列,可使用
list(列表)或deque(双端队列)来模拟队列,只要遵循队列的标准操作逻辑即可。
解析:
那么经过了上面的题意分析,我们也就知道,其实这道题的本质就是,我们要用两个队列,去实现栈的基本功能,尾插,尾取,尾删等等的操作。
那么具体我们要怎么实现呢,诶大家,还记得我第一篇讲数据结构所说的吗,数据结构这个专栏,最重要的就是画图分析,无论你有没有思路,都烦请你画个图,这会对你的思路产生极大的帮助,当然,如果你是天才,那就当我没说~
所以对于这道题,我们依旧是可以用画图来进行分析,我们先画出两个队列,接下来,我们来对题目所要求的要实现的栈的基本功能,一个一个的来分析。
对两个队列的创建(初始化):
大家其实可以看到,题目是要求我们把两个队列存储在一个结构体中的,所以在那个结构体中,我们就要先创建两个队列结构体(注意:不是链表结构体,是存放头指针和尾指针以及size的那个结构体)(这里也要注意,在这里我们是直接创建结构体变量 而不是结构体指针变量,所以不需要为这两个变量申请空间,如果创建的是结构体指针变量的话,就需要申请空间哦大家),然后在下一个函数,也就是这个函数中,我们要记得创建存储两个队列的结构体的指针变量(一定要记得给这个指针申请空间),然后再调用队列初始化函数,去把那个结构体中的两个队列都给初始化掉~perfect~,具体代码如下:
typedef struct {que q1;que q2;} MyStack;MyStack* myStackCreate() {MyStack* obj=(MyStack*)malloc(sizeof(MyStack));qninit(&(obj->q1));qninit(&(obj->q2));return obj;}对栈进行插入数据(尾插):
这一部分,其实没什么难度的大家,我们就往我们的其中一个队列尾插进数据就行,就像下图这样子: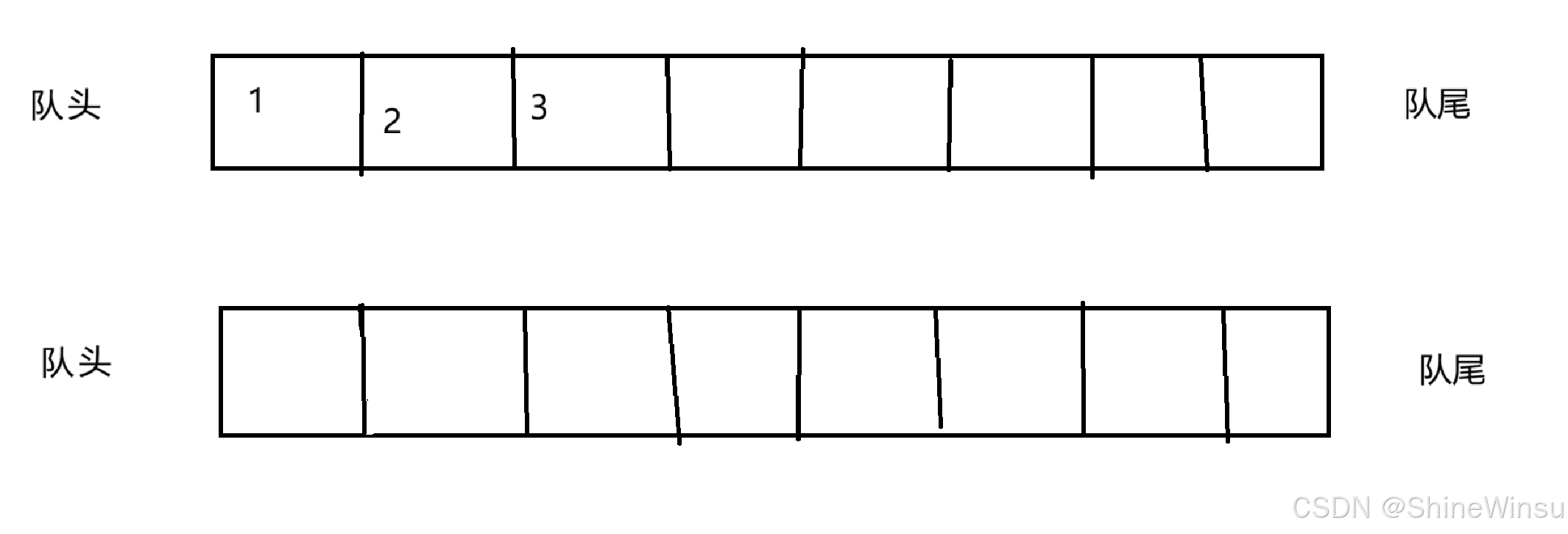
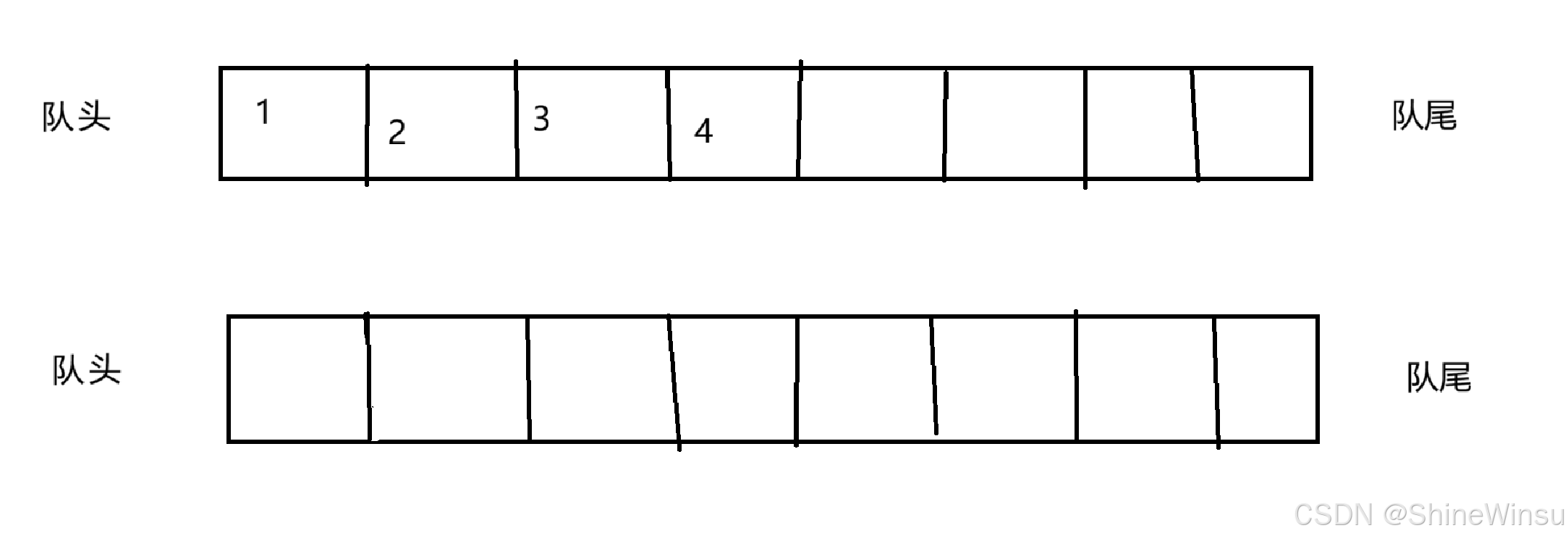
这个是没什么的,大家可千万不要搁那,诶,我一个数据放第一个队列,我另一个数据放第二个队列,这可是很离谱也很无敌的操作哇。
准确来说,因为是有两个队列,所以我们是要看哪个队列不为空,就往哪个队列插入数据,这样子才算是妥善的尾插(其实这个时候,那个不为空的队列,我们可以短暂的把其当作栈,只不过尾插依旧是用队列的尾插操作)。
那么这个时候,聪明的大家肯定就有疑问了,诶,为什么要往不为空的队列插入数据呢,难道还有为空的队列?是的诸位,不难为什么题目要求我们用两个队列去实现栈呢?哈哈,那么又为什么会出现一个为空的队列,一个不为空的队列呢?其实这就和我们要讲的利用两个队列实现栈的删除(尾删)操作有关了。
我们先看尾插的代码:
void myStackPush(MyStack* obj, int x) {//哪个队列不为空,就要往哪个队列去插入数据if(qnempty(&(obj->q1))==false){qnpush(&(obj->q1),x);}else{qnpush(&(obj->q2),x);}
}对栈删除数据(尾删):
那么可以这么说,这一部分,才算是本题唯一的难点,我们知道,栈遵循着后进先出的要求,就好比下面这幅图
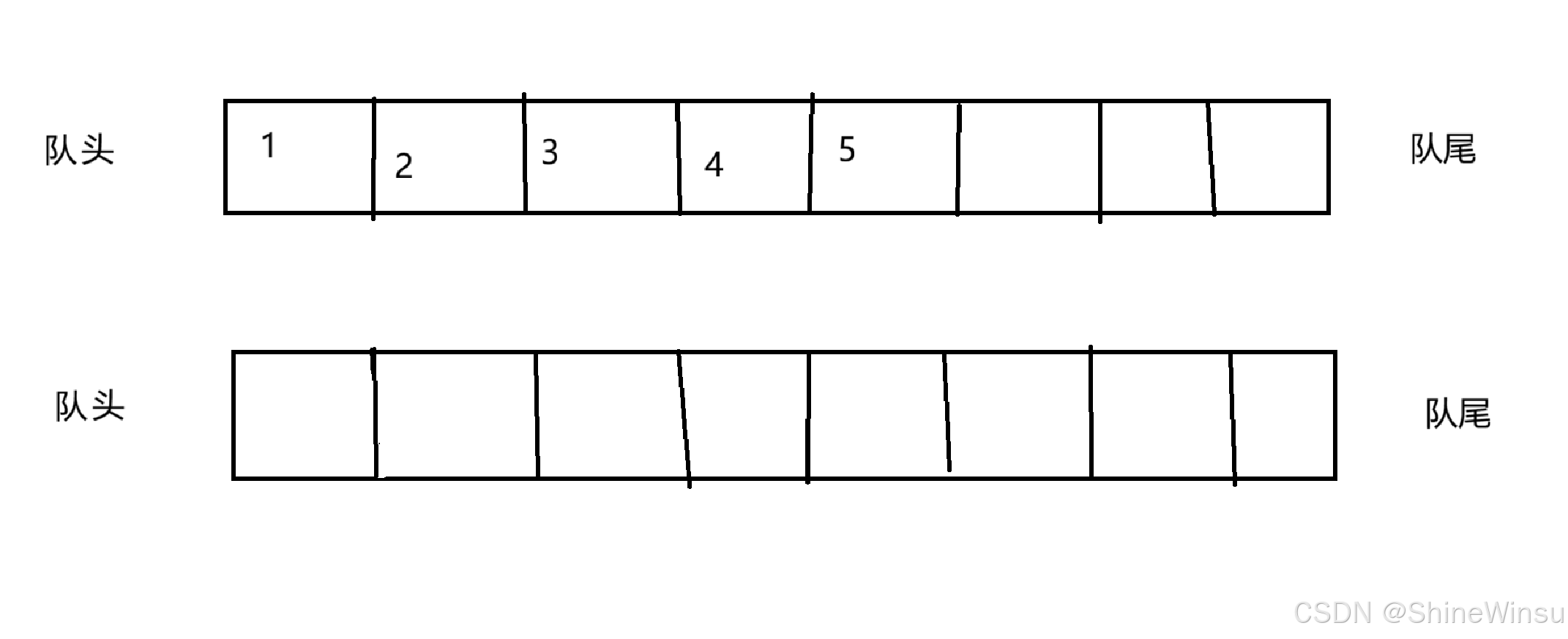
我们要让最后的5删除掉,但是由于我们是用队列实现,而队列可没有尾删的操作,所以呢,这个时候,我们的两个队列就派上用场了,大家接下来看我的示例图以及讲解,保证大家瞬间搞懂如何实现这一部分:
首先,我们原始的情况下,两个队列是长这样子
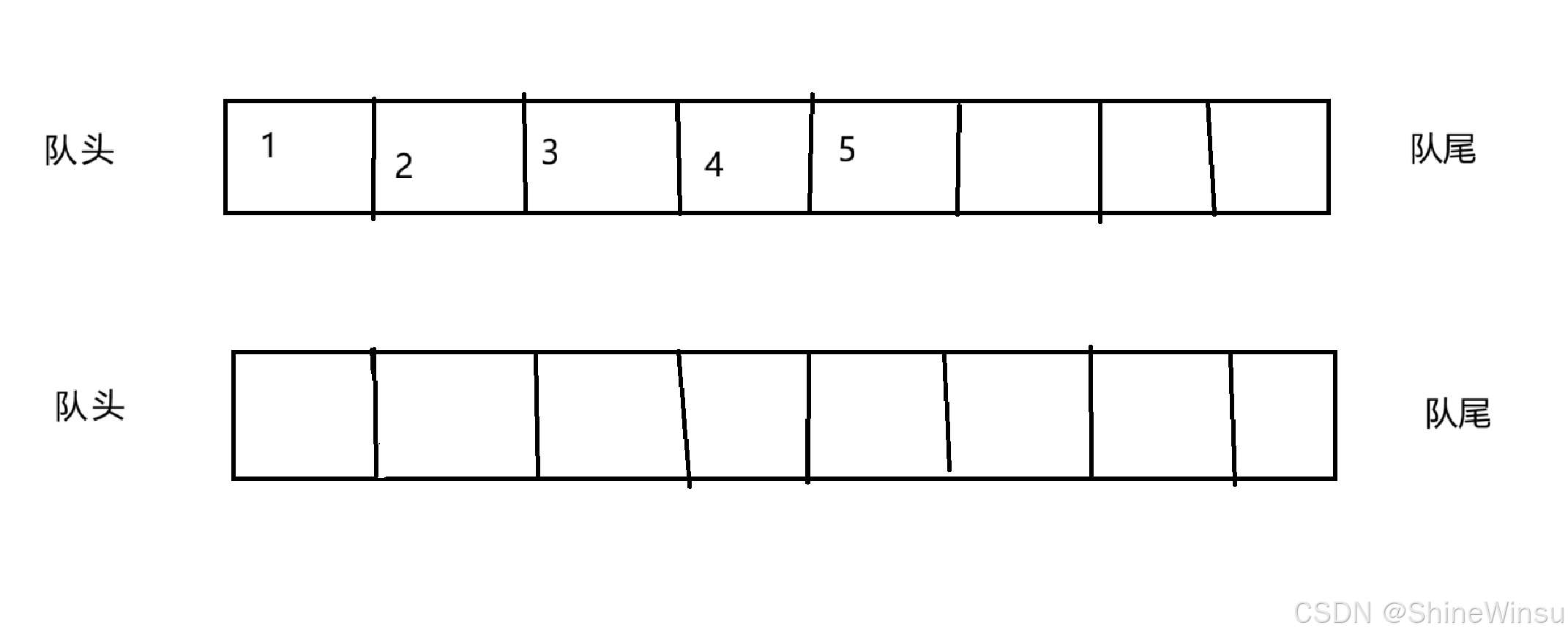
然后,我们要想办法把最后的5给它干掉,同时前面的1 2 3 4不能动,而且最重要的是,1 2 3 4的顺序也不能动,那么这个时候,我们就可以利用另一个空的队列了,大家看图:
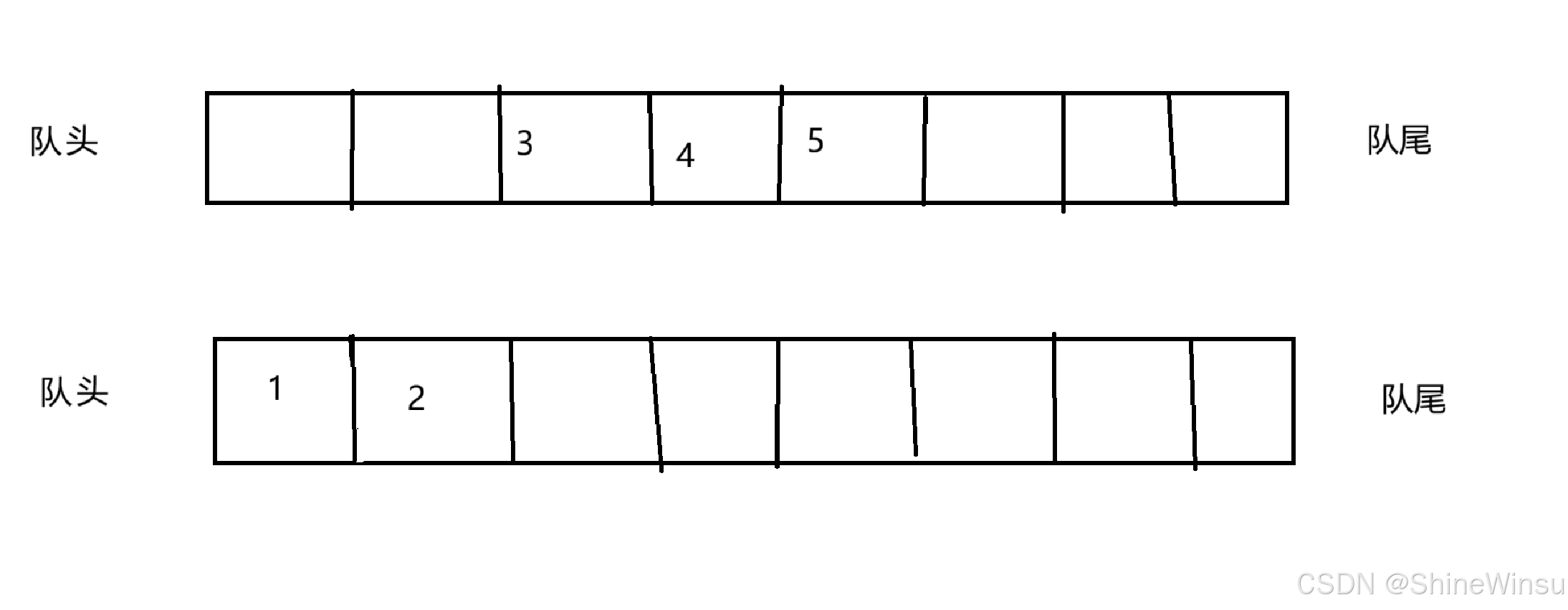
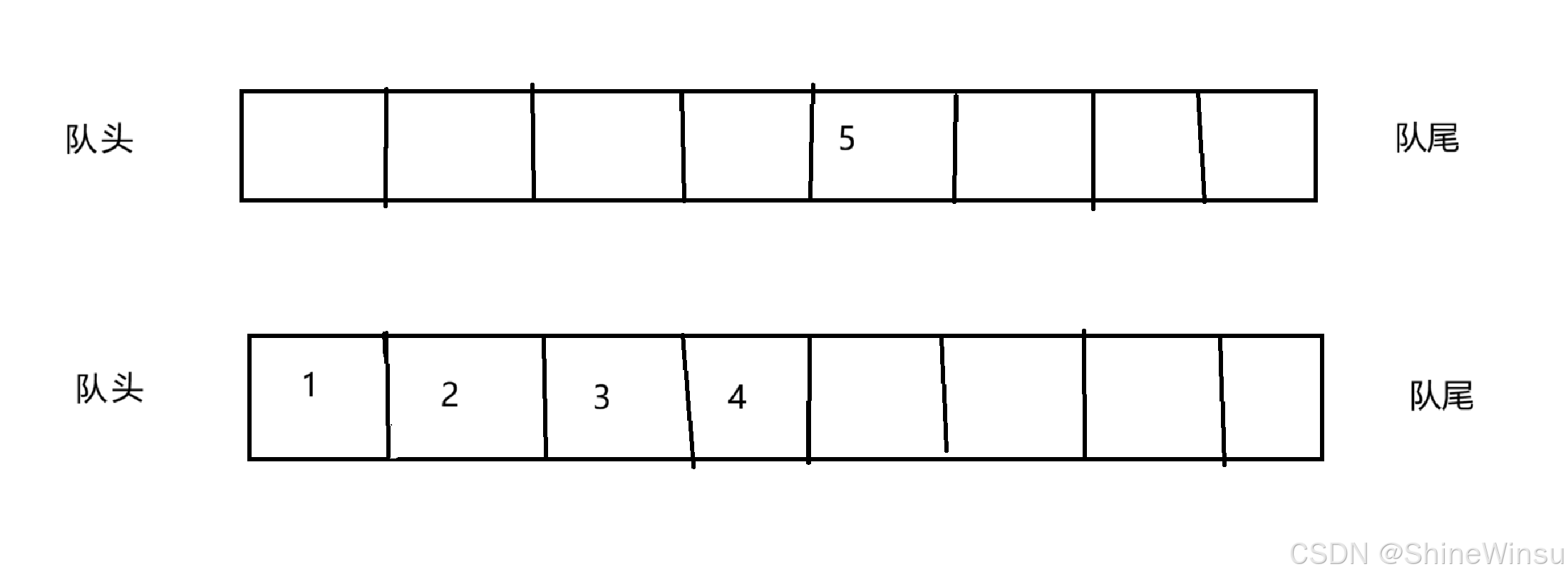
我们这样子一个一个的把不为空的那个队列的元素,分别取出它的队头的元素,然后再把那个元素尾插(即队尾插入)为空的那个队列,并且我们完成一次对为空队列的尾插之后,我们就把不为空的那个队列给头删一下(即对头删除) 当删除到原本不为空的那个队列只剩最后一个数据(也就是我们栈要删除的数据)之后,我们就不把那个数据传进原本为空的那个链表中,直接给他删除掉,就像下图: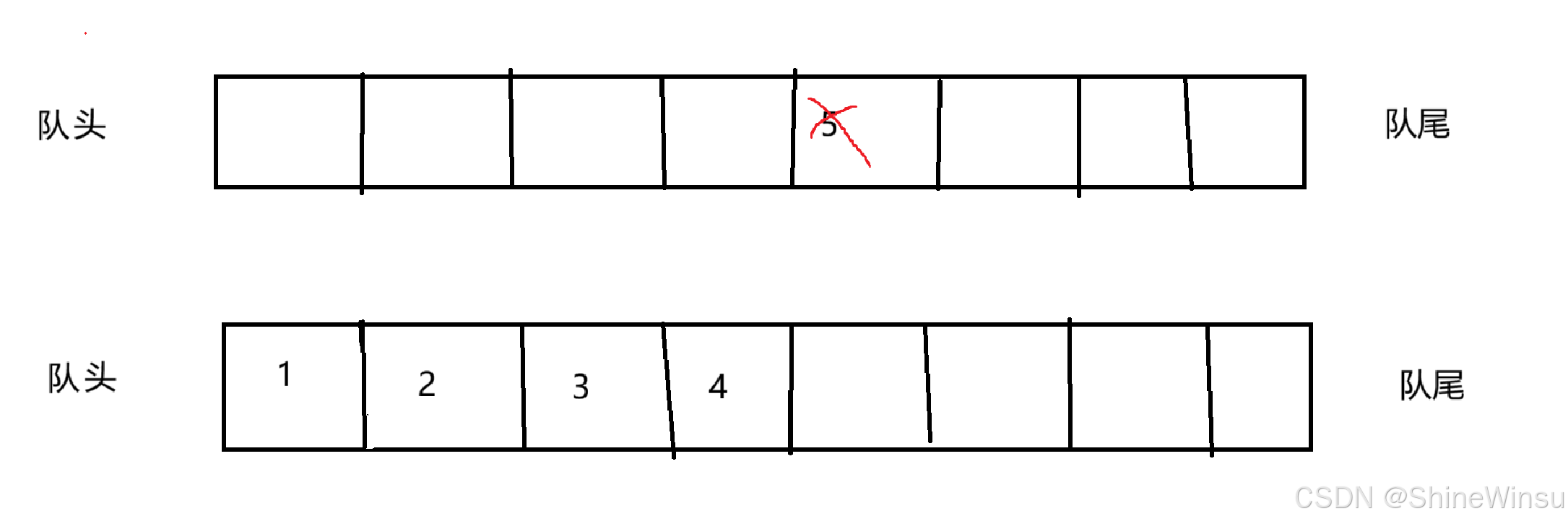
那么这么一来,新的不为空的队列(即原本为空的队列),就算作是新的临时栈,那么大家看图之后,可以发现,新的临时栈的数据排列顺序以及数据个数是完全符合我们对一个栈进行尾删之后的操作的。
怎么样,大家,是不是一下子就醍醐灌顶了?
那么我们进行队列数据转移的循环条件是什么呢?(可不要说不知道还要循环),其实就是原本非空的那个队列的数据个数大于1,只要还大于1,我们就转移数据,当原本的不为空的那个队列只剩下一个数据时,我们再出循环,去把那个数据给删除掉,如此一来,我们便能完美实现上面所说的操作~大家明白了不~~~
注意,上面所说的各个操作,我们的队列中的函数,都是有的,所以我们可以直接调用队列函数进行使用哦。
那么在我给出完整代码之前,还有一个问题需要解决,那就是,我们要怎么知道两个队列哪一个是空队列,哪一个是非空队列呢?
诶大家,其实这个很简单的,我们既可以使用if去分别判断q1和q2是否为空,也可以使用假设法去进行判断,这个也是我个人比较推荐的(因为用这个方法比较有逼格,符合我的个人形象~),而假设法,我在之前的题目解析中,有提到过,想必大家并不陌生(陌生就代表you no 逼格~),哈哈哈。
那么接下来,我就直接给出完整代码:
int myStackPop(MyStack* obj) {//将不为空的栈的d到最后一个前面的数据都丢到为空的那一个栈//使用假设法que* empty = &(obj->q1);que* noempty = &(obj->q2);if(qnempty(&(obj->q2))){empty=&(obj->q2);noempty=&(obj->q1);}while(noempty->size>1){qnpush(empty,qnfront(noempty));qnpop(noempty);//要记得删除非空队列的数据}int ret=qnfront(noempty);qnpop(noempty);//删除不为空的队列(此时就剩一个数据)的数据return ret;
}对栈的数据取用(栈顶,尾取):
大家,这个我觉得并不难吧,经过上面的图分析之后,我们知道,其实非空那么一个队列,就相当于是临时栈,顺序也是对的,所以,我可以直接用队列的尾取函数去取出那个非空队列的队尾元素就行啦大家~
详细代码如下:
int myStackTop(MyStack* obj) {que* empty=&(obj->q1);que* noempty=&(obj->q2);if(qnempty(&(obj->q2))){empty=&(obj->q2);noempty=&(obj->q1);}return qnback(noempty);
}对栈的销毁:
那么大家,其实这个销毁是简单的没边了,我们只需要先把那两个队列给销毁了,再把存储这两个队列的结构体给销毁掉就行,代码如下:
完整代码:
void myStackFree(MyStack* obj) {//要先把队列给释放了//再去释放objqnbreak(&(obj->q1));qnbreak(&(obj->q2));free(obj);
}完整代码:
那么到了这里,这道题也就大功告成了,下面我就给出完整代码:
//队列概念:只允许在一端进行插入数据操作,
//在另一端进行删除数据操作的特殊线性表,
//队列具有先进先出FIFO(First In First Out)
//入队列:进行插入操作的一端称为队尾
//出队列:进行删除操作的一端称为队头
//但是我们取出队列中的数据却是可以取队头的数据
//也可以取队尾的数据typedef int name1;//我们创建队列,是使用单向链表来进行实现
//因为如果使用顺序表(数组)的话,我们既要尾插,又要头删
//要进行数组的数据的不断循环移动,太消耗cpu
//而相对而言,单向链表的尾插头删等操作,就显得美妙多了
//它只需要改变指针方向并释放节点就行
//至于为什么不用双向链表,那是因为这家伙多了一个指针,
//占用空间大,所以我们不要struct queuenode
{name1 data;//存储数据struct queuenode* next;//指向下一个节点的指针
};typedef struct queuenode qn;//因为我们要对队列(本质算是单向链表)进行尾插和头删
//我们之前单向链表是只传入头结点指针
//那么这对我们队列来说,每次尾插都要遍历,太麻烦
//所以我们直接创建单向链表的尾节点指针
//那么这么一来就有两个指针了
//我们可以把它们放进结构体中进行维护struct queue
{qn* phead;qn* ptail;int size;//这个size是为了我们后续统计队列中一共有几个数据准备的//我们如果不用size的话,我们想要知道队列中有几个数据//就得去遍历队列,太过麻烦//而我们使用size的话,尾插时就++,头删时就--//最后统计队列数据个数的时候,直接将size返回就行了};typedef struct queue que;//这边注意,由于我们把队列中所需要的一些数据全部丢到结构体que中了
//所以我们函数的参数就可以直接传结构体即可//对队列的初始化
void qninit(que* ps);//对队列的销毁
void qnbreak(que* ps);//对队列队尾的插入数据
void qnpush(que* ps,name1 x);//对队列队头的删除数据
void qnpop(que* ps);//对队列队头数据的取用
name1 qnfront(que* ps);//对队列队尾数据的取用
name1 qnback(que* ps);//统计队列中的数据个数
int qnsize(que* ps);//判断队列是否为空
bool qnempty(que* ps);//对队列的初始化
void qninit(que* ps)
{// assert(ps);ps->phead = NULL;ps->ptail = NULL;ps->size = 0;//直接初始化为空即可
}//对队列的销毁
void qnbreak(que* ps)
{assert(ps);while (ps->phead != NULL){qn* nexttemp = ps->phead->next;free(ps->phead);ps->phead = nexttemp;}ps->phead = NULL;ps->ptail = NULL;ps->size = 0;
}//对队列队尾的插入数据
void qnpush(que* ps,name1 x)
{qn* newqn = (qn*)malloc(sizeof(qn));if (newqn == NULL){perror("malloc newqn false:");exit(1);}newqn->data = x;newqn->next = NULL;if (ps->size == 0)//如果队列中没有数据{ps->phead = newqn;ps->ptail = ps->phead;}else{//进行尾插:ps->ptail->next = newqn;ps->ptail = ps->ptail->next;}//要记得size++哦ps->size++;}//对队列队头的删除数据(头删)
void qnpop(que* ps)
{assert(ps);//检验队列中有没有数据//如果没有,那删个鸡毛assert(ps->size>0);qn* nextemp = ps->phead->next;//保存第二个节点的地址//如果只有一个节点时,就要两个指针都指向NULL,//不难有多个节点的话,我们是不会令ps->ptai指向空if (ps->phead->next==NULL){free(ps->phead);//不用free ps->ptail,因它们两个对应的节点是同一个ps->phead = NULL;ps->ptail = NULL;}else {free(ps->phead);//要记得将头结点指针修改为指向原队列的第二个节点ps->phead = nextemp;}//要记得对size--ps->size--;}//对队列队头数据的取用
name1 qnfront(que* ps)
{assert(ps);//检验队列中有没有数据//如果没有,那取个鸡毛assert(ps->size>0);//直接返回头结点的数据即可return ps->phead->data;
}//对队列队尾数据的取用
name1 qnback(que* ps)
{assert(ps);//检验队列中有没有数据//如果没有,那取个鸡毛assert(ps->size>0);//直接返回尾结点的数据即可return ps->ptail->data;
}//统计队列中的数据个数
int qnsize(que* ps)
{assert(ps);return ps->size;
}//判断队列是否为空
bool qnempty(que* ps)
{assert(ps);if (ps->size == 0){return true;}else{return false;}
}typedef struct {que q1;que q2;} MyStack;MyStack* myStackCreate() {MyStack* obj=(MyStack*)malloc(sizeof(MyStack));qninit(&(obj->q1));qninit(&(obj->q2));return obj;}void myStackPush(MyStack* obj, int x) {//哪个队列不为空,就要往哪个队列去插入数据if(qnempty(&(obj->q1))==false){qnpush(&(obj->q1),x);}else{qnpush(&(obj->q2),x);}
}int myStackPop(MyStack* obj) {//将不为空的栈的d到最后一个前面的数据都丢到为空的那一个栈//使用假设法que* empty = &(obj->q1);que* noempty = &(obj->q2);if(qnempty(&(obj->q2))){empty=&(obj->q2);noempty=&(obj->q1);}while(noempty->size>1){qnpush(empty,qnfront(noempty));qnpop(noempty);//要记得删除非空队列的数据}int ret=qnfront(noempty);qnpop(noempty);//删除不为空的队列(此时就剩一个数据)的数据return ret;
}int myStackTop(MyStack* obj) {que* empty=&(obj->q1);que* noempty=&(obj->q2);if(qnempty(&(obj->q2))){empty=&(obj->q2);noempty=&(obj->q1);}return qnback(noempty);
}bool myStackEmpty(MyStack* obj) {return qnempty(&(obj->q1))&&qnempty(&(obj->q2));
}void myStackFree(MyStack* obj) {//要先把队列给释放了//再去释放objqnbreak(&(obj->q1));qnbreak(&(obj->q2));free(obj);
}/*** Your MyStack struct will be instantiated and called as such:* MyStack* obj = myStackCreate();* myStackPush(obj, x);* int param_2 = myStackPop(obj);* int param_3 = myStackTop(obj);* bool param_4 = myStackEmpty(obj);* myStackFree(obj);
*/使用栈实现队列:
坦白的说,这道题其实我个人觉得 是要比上面的用队列实现栈更有难度,我们先看题目:

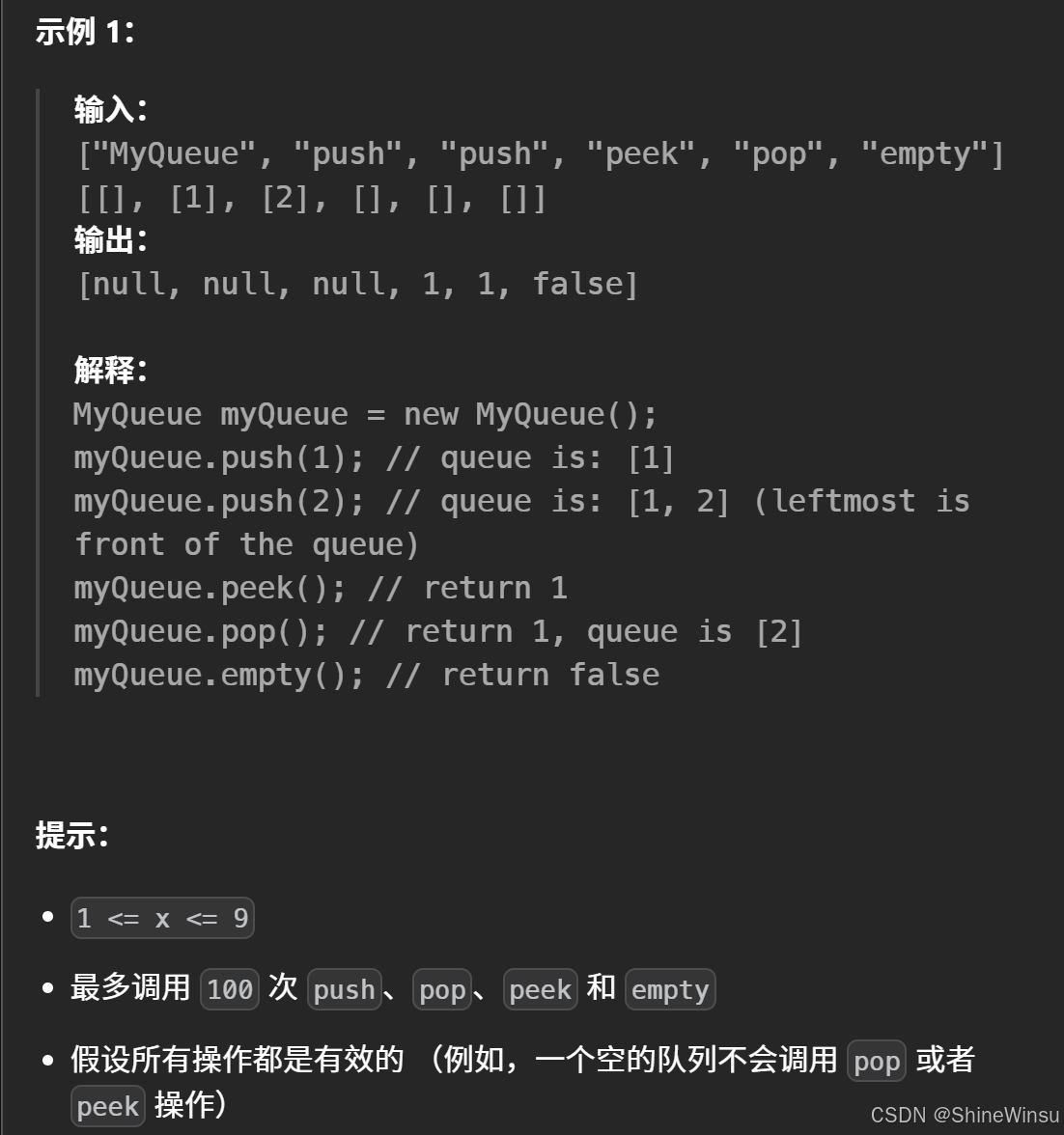
题意分析:
这道题要求仅使用两个栈来实现一个 ** 先入先出(FIFO)** 的队列,并支持队列的四种基本操作:push(元素推到队列末尾)、pop(从队列开头移除并返回元素)、peek(返回队列开头的元素)、empty(判断队列是否为空)。
关键限制
- 只能使用标准的栈操作,即
push to top(栈顶入栈)、peek/pop from top(栈顶查看 / 出栈)、size(栈大小)、is empty(栈是否为空)。 - 如果所用语言不支持栈,可使用
list(列表)或deque(双端队列)来模拟栈,只要遵循栈的标准操作逻辑即可。
解析:
那么大家经过了题意分析之后,也是知道了,这道题也是要求我们使用两个栈去实现一个队列,即利用两个栈的先进后出,去实现一个队列的先进先出。
那么,对于这道题,我们肯定也是延续着我们的优秀作风,直接画图分析(啊♥伟大的画图啊,请赐予我战胜一切,一往无前的力量吧!!!),我们先给出两个初始图: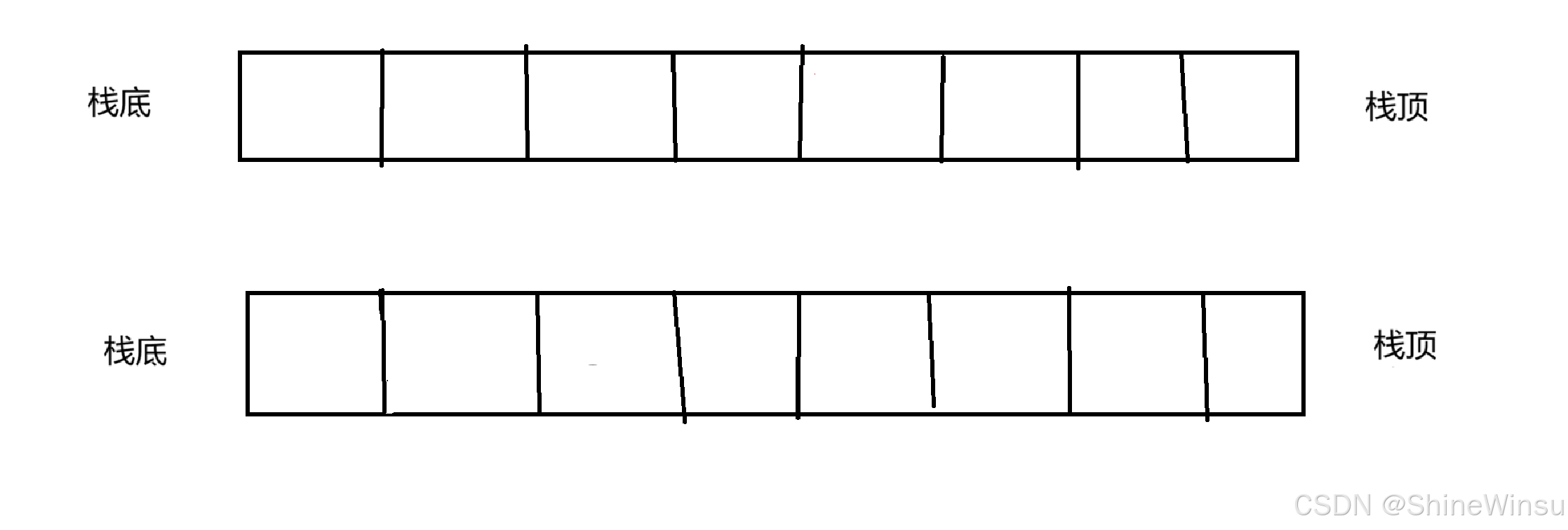
对于两个栈的创建:
如上面那道题一样,这道题也是要把两个栈存储在一个结构体中,那么那么,我在这里是用的栈结构体指针变量,所以我后续得为它们两个申请内存空间,那如果大家是直接用的结构体变量的话,那么大家就可以不用申请。
接下来就是要对我们存储两个栈的结构体申请内存空间,然后我们接下来就可以开始这两个栈为所欲为了哈哈哈。
下面是详细代码:
typedef struct {st* s1;st* s2;} MyQueue;MyQueue* myQueueCreate() {MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));//由于我们上面创建的是指针类型,而不是结构体类型//指针类型的话,需要我们去申请内存//结构体类型则不需要我们去申请内存obj->s1=(st*)malloc(sizeof(st));obj->s2=(st*)malloc(sizeof(st));//进行初始化stinit(obj->s1);stinit(obj->s2);return obj;
}对于队列的判空:
这个很简单,我们直接看是不是两个栈都是为空,如果两个栈都为空的话,恭喜队列,你是空的,详细代码如下:
bool myQueueEmpty(MyQueue* obj) {return stempty(obj->s1)&&stempty(obj->s2);
}对于队列的尾插:
其实和上一题类似,两个栈,有数据的那个栈,可以充当临时的队列,所以,针对于我们这个队列的数据插入,也就是尾插,我们可以直接对有数据的那个栈进行尾插数据即可,就如下图: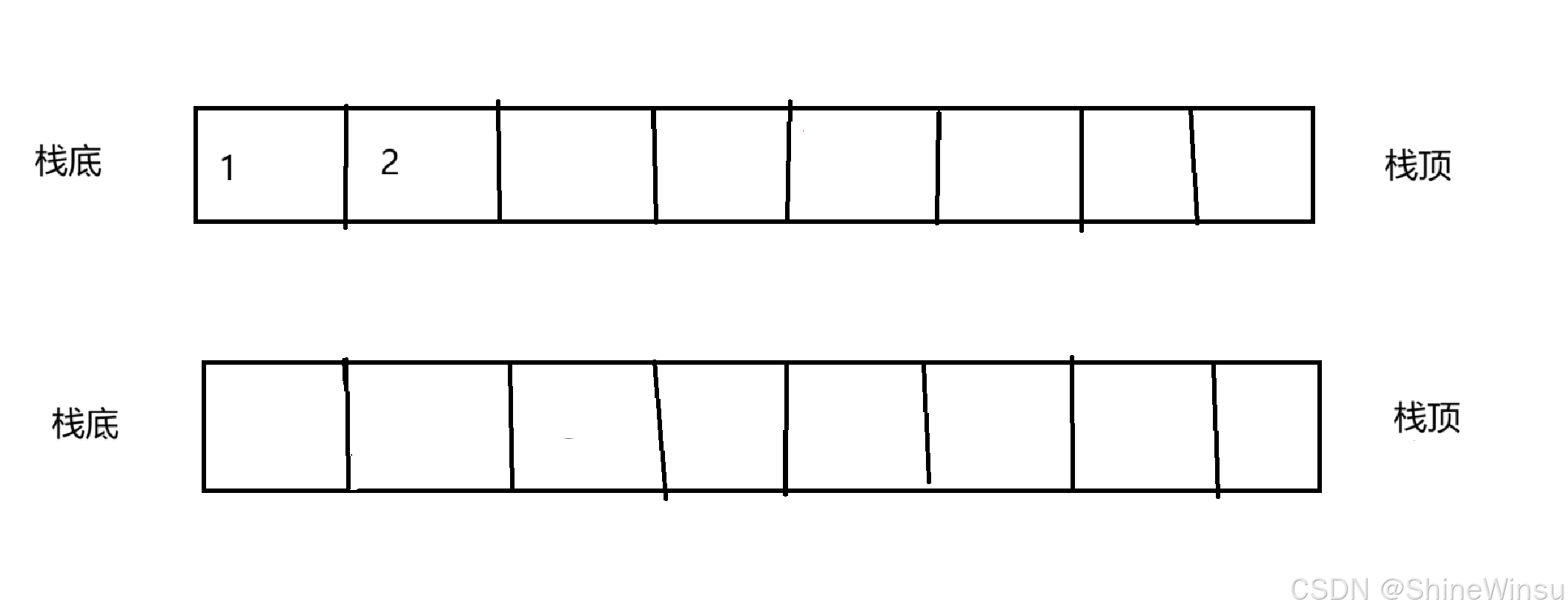
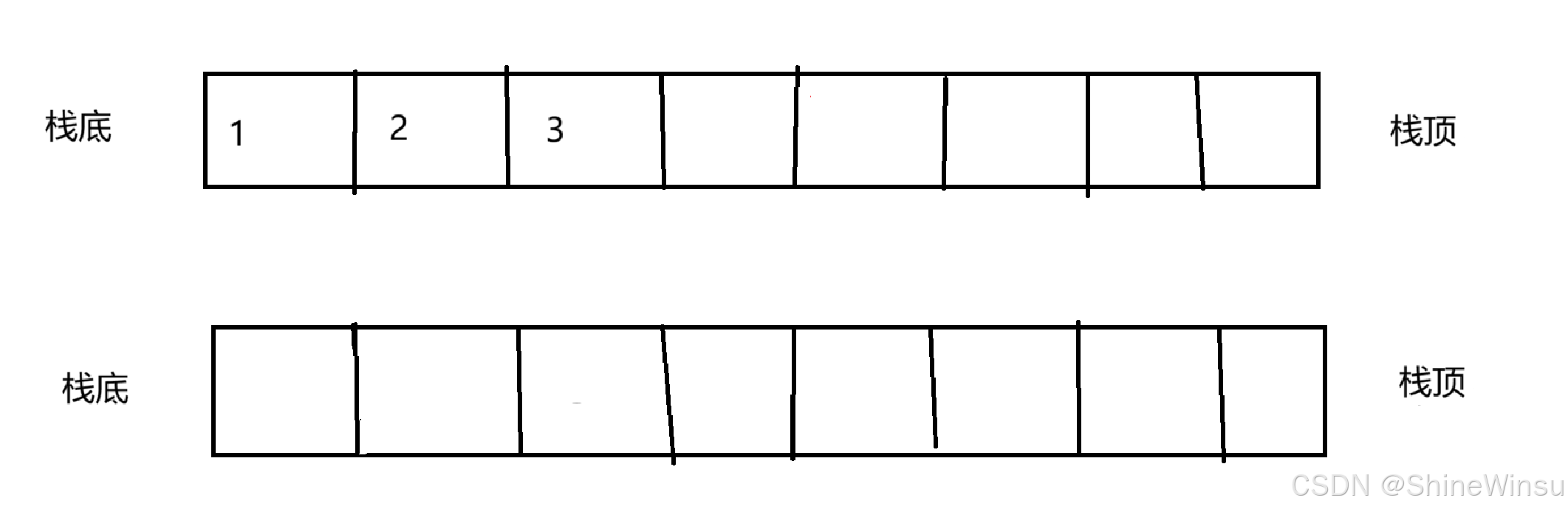
下面是详细代码:
void myQueuePush(MyQueue* obj, int x) {//依旧是哪个不为空,就往哪个插入数据//也可以使用假设法if(stsize(obj->s1)!=0){stpush(obj->s1,x);}else{stpush(obj->s2,x);}
}对于队列的头删:
这一个,才是本题的难点,之所以是难点的原因就在于,我们又要保持队列的数据顺序不能变,又要保证能进行头删,最最主要的还是因为,栈只能取尾,尾删,即只能对栈顶操作,并不能直接对栈底操作。
这就又需要我们对那两个队列进行为所欲为的操作了,同样的道理,我们要把非空的那个栈的数据进行转移(依旧是用假设法去判断哪个栈是空的哦),但是由于我们的栈只能尾插,尾取,所以当我们从非空栈通过尾取去尾插进空栈中时,大家可以看到,两个栈由这样子
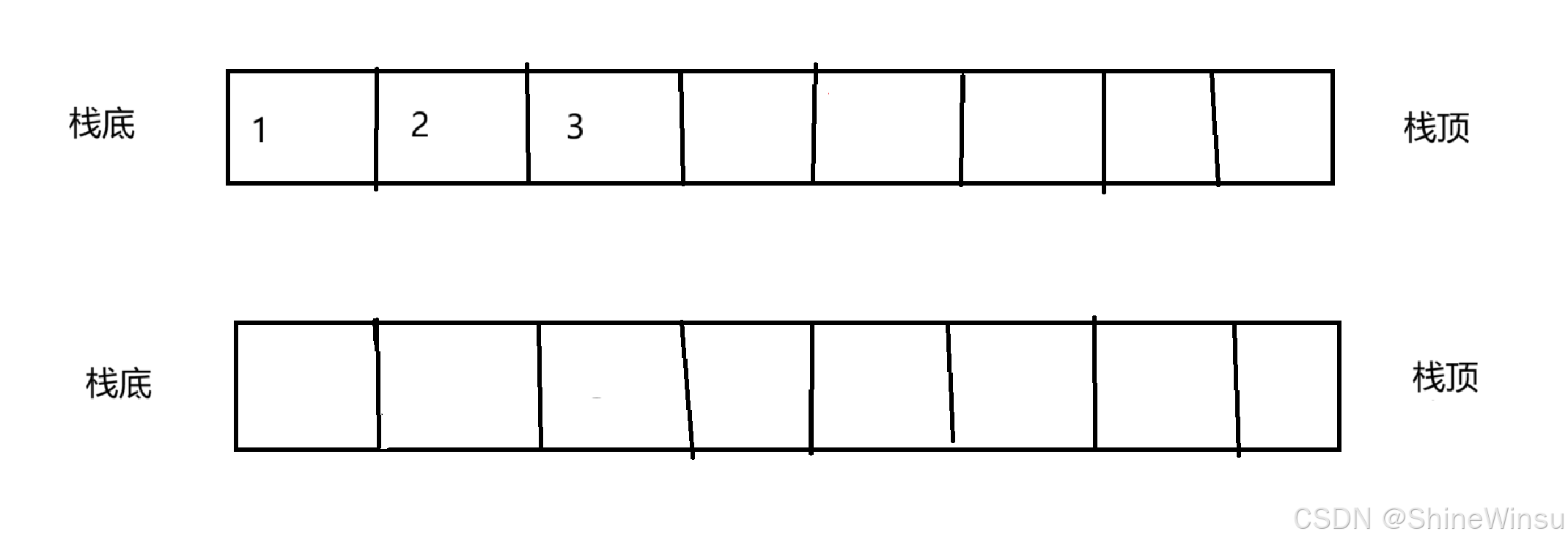
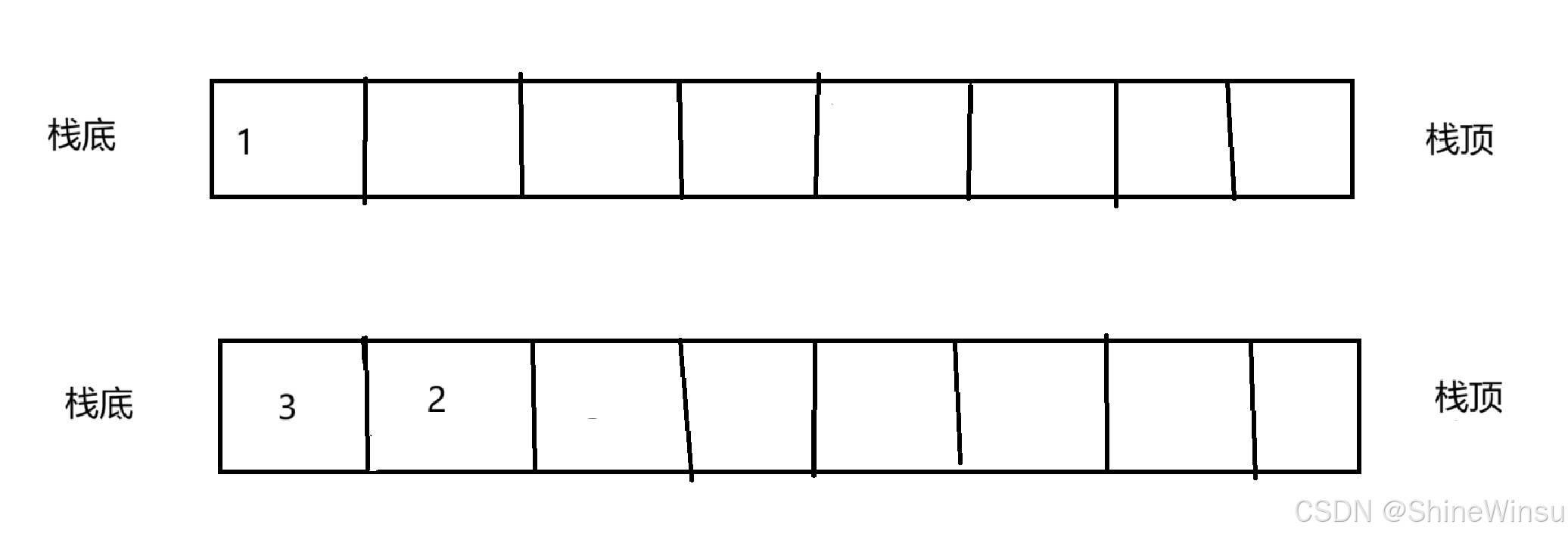
变成了这样子,那么如果我们后续要再进行队列的队头取操作或者出队(尾删)操作时,再按照上面所说的操作进行的话,大家就会发现,wdf,顺序不符合最开始队列的顺序呀。
那么,这个,我们要怎么办呢?怎么办呀怎么办~怎么办呀怎么办~,哈哈哈,不要慌大家,我们在进行了一次栈数据转移之后 顺序和原本颠倒了,那我们就再进行一次栈数据转移呗,所谓负负得正,就像这样子,那么这样子,是不是就完美恢复到了最初的队列顺序了大家?当然,大家不要忘记了要再进行一次假设法判空,因为经过第一轮转移之后,原本的empty已经变为noempty了,所以,这就需要我们再次使用假设法。
而且大家要知道,我们的第一次转移是要转移到非空栈中只剩一个数据,并且转一个删一个,而我们的第一次转移,则是要转移到非空栈中一个数据不剩,同样也是转一个删一个,如此一来,我们才能完美实现这个功能~
好了,大家请看详细的代码:
int myQueuePop(MyQueue* obj) {//我们依旧是进行转移//将非空的栈中的数据转移到为空的栈中st* empty=obj->s1;st* noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>1){stpush(empty,sttop(noempty));//要记得删除我们非空栈中的转移的数据stpop(noempty);}int ret=sttop(noempty);//要记得删除干净stpop(noempty);//再转移一次empty=obj->s1;noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>0){stpush(empty,sttop(noempty));//要记得删除我们非空栈中的转移的数据stpop(noempty);}return ret;
}对队列的头取操作:
说实话,我觉得这个也挺麻烦的,至于它的思路,是和上面一样的,也是要转移两次,只不过不删数据罢了,大家看了代码就能理解:
int myQueuePeek(MyQueue* obj) {//对队列元素的取出//即先进先出st* empty=obj->s1;st* noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>0){stpush(empty,sttop(noempty));stpop(noempty);} empty=obj->s1;noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}name1 ret=sttop(noempty);//再转移回去,不难顺序会乱while(stsize(noempty)){stpush(empty,sttop(noempty));stpop(noempty);}return ret;
}对队列的销毁:
不必多说不必多说,先收释放小弟,再释放老大,和上面那道题如出一辙,简单简单,直接看详细代码:
void myQueueFree(MyQueue* obj) {//也是要先释放小的,再释放大的stdestroy(obj->s1);stdestroy(obj->s2);free(obj);
}完整代码:
ok,到了这里,我们这道题就大功告成了,下面给出完整代码
//栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。
//进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。
//栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
//压栈:栈的插入操作叫做进栈 / 压栈 / 入栈,入数据在栈顶。
//出栈:栈的删除操作叫做出栈。出数据也在栈顶。//栈其实就是类似弹夹,我们把子弹插入,然后最后插入的子弹最先射出去
//最先插入的子弹反而最后射出去,这就是栈typedef int name1;//栈底层结构选型
//栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。
//因为数组在尾上插入数据的代价比较小。//所以我们选择把数组的尾部当作我们栈的栈顶
//所以我们对栈的输入(即在栈顶输入数据)就相当于是对数组的尾插
//而对栈的删除(即在栈顶删除数据)就相当于是对数组的尾删
//而对栈顶的元素的取用,也是当作对数组尾部元素的取用。struct stack
{name1* arr;//创建数组,动态数组,所以用指针int top;//其实就相当于是数组的有效数据个数,//只不过我们用top代表栈顶,其实就是数组的尾部//在这里我们针对top的初始化要格外的注意//因为我们知道,栈中的栈顶指向的是栈的最上面的最高一个有效数据,注意:是有效数据//而我们又知道,数组储存数据是从0开始存储的//换句话说就是,我们的top下标对应的数组元素是没有数据的//top-1下标所对应的数组元素才是数组中最后一个有效数据,也就相当于是栈顶//top为0的时候,它是指向栈顶元素的下一个//上面是top=0的情况,其实就和我们的顺序表如出一辙//那么如果我们想让top指向的是数组中最后一个有效数据,也就相当于是栈顶//那么我们就得初始化top为-1,因为top为0的时候,它是指向栈顶元素的下一个//当然这边是推荐用top=0,因为这样子就和顺序表差不多,便于我们理解int capacity;//数组的有效空间
};typedef struct stack st;//对栈的初始化
void stinit(st* ps);//对栈的销毁
void stdestroy(st* ps);//对栈顶的插入(即数组尾插)
void stpush(st* ps,name1 x);//对栈顶的删除(即数组尾删)
void stpop(st* ps);//对栈顶的取用
name1 sttop(st* ps);//统计栈的数据个数
int stsize(st* ps);//判断栈是否为空
bool stempty(st* ps);
//使用bool记得要包含stdbool.h头文件//对栈的初始化
void stinit(st* ps)
{//依旧检验是否为空指针assert(ps);//其实和顺序表的初始化一样ps->arr = NULL;ps->top = 0;//在这里我们针对top的初始化要格外的注意//因为我们知道,栈中的栈顶指向的是栈的最上面的最高一个有效数据,注意:是有效数据//而我们又知道,数组储存数据是从0开始存储的//换句话说就是,我们的top下标对应的数组元素是没有数据的//top-1下标所对应的数组元素才是数组中最后一个有效数据,也就相当于是栈顶//top为0的时候,它是指向栈顶元素的下一个//上面是top=0的情况,其实就和我们的顺序表如出一辙//那么如果我们想让top指向的是数组中最后一个有效数据,也就相当于是栈顶//那么我们就得初始化top为-1,因为top为0的时候,它是指向栈顶元素的下一个//当然这边是推荐用top=0,因为这样子就和顺序表差不多,便于我们理解ps->capacity = 0;
}//对栈的销毁
void stdestroy(st* ps)
{assert(ps);//因为我们是直接动态申请来的arr//换句话来说就是我们整个过程中,都只对arr这个指针进行申请空间//所以直接free掉arr就相当于是把整个创建的数组空间销毁掉free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}//判断数组(栈)空间够不够,不够就申请新空间的函数
void createarr(st* ps)
{int newcapacity = ps->capacity == 0 ? 2 : 2 * ps->capacity;name1* newarr = (name1*)realloc(ps->arr, sizeof(name1) * newcapacity);if (newarr == NULL){perror("realloc error");exit(1);}ps->capacity = newcapacity;ps->arr = newarr;}//对栈顶的插入(即数组尾插)
void stpush(st* ps,name1 x)
{//判断链表空间够不够的函数if (ps->capacity == ps->top){createarr(ps);}ps->arr[ps->top] = x;ps->top++;//其实就和顺序表尾插一模一样}//对栈顶的删除(即数组尾删)
void stpop(st* ps)
{//检验是不是空指针assert(ps);//检验栈中数据是否为空//为空还删个鸡毛assert(ps->top > 0);ps->top--;///也和顺序表尾删一模一样
}//对栈顶的取用
name1 sttop(st* ps)
{//检验是不是空指针assert(ps);//检验栈中数据是否为空//为空还取个鸡毛的栈顶数据assert(ps->top > 0);return ps->arr[ps->top - 1];
}//统计栈的数据个数
int stsize(st* ps)
{//检验是不是空指针assert(ps);int count = 0;count = (ps->top);//根据顺序表知识,我们知道,top其实就相当于是顺序表的有效数据个数return count;
}//判断栈是否为空
bool stempty(st* ps)
{if (ps->top == 0){return true;}else{return false;}
}
//使用bool记得要包含stdbool.h头文件typedef struct {st* s1;st* s2;} MyQueue;MyQueue* myQueueCreate() {MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));//由于我们上面创建的是指针类型,而不是结构体类型//指针类型的话,需要我们去申请内存//结构体类型则不需要我们去申请内存obj->s1=(st*)malloc(sizeof(st));obj->s2=(st*)malloc(sizeof(st));//进行初始化stinit(obj->s1);stinit(obj->s2);return obj;
}void myQueuePush(MyQueue* obj, int x) {//依旧是哪个不为空,就往哪个插入数据//也可以使用假设法if(stsize(obj->s1)!=0){stpush(obj->s1,x);}else{stpush(obj->s2,x);}
}int myQueuePop(MyQueue* obj) {//我们依旧是进行转移//将非空的栈中的数据转移到为空的栈中st* empty=obj->s1;st* noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>1){stpush(empty,sttop(noempty));//要记得删除我们非空栈中的转移的数据stpop(noempty);}int ret=sttop(noempty);//要记得删除干净stpop(noempty);//再转移一次empty=obj->s1;noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>0){stpush(empty,sttop(noempty));//要记得删除我们非空栈中的转移的数据stpop(noempty);}return ret;
}int myQueuePeek(MyQueue* obj) {//对队列元素的取出//即先进先出st* empty=obj->s1;st* noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}while(stsize(noempty)>0){stpush(empty,sttop(noempty));stpop(noempty);} empty=obj->s1;noempty=obj->s2;if(stsize(obj->s2)==0){empty=obj->s2;noempty=obj->s1;}name1 ret=sttop(noempty);//再转移回去,不难顺序会乱while(stsize(noempty)){stpush(empty,sttop(noempty));stpop(noempty);}return ret;
}bool myQueueEmpty(MyQueue* obj) {return stempty(obj->s1)&&stempty(obj->s2);
}void myQueueFree(MyQueue* obj) {//也是要先释放小的,再释放大的stdestroy(obj->s1);stdestroy(obj->s2);free(obj);
}/*** Your MyQueue struct will be instantiated and called as such:* MyQueue* obj = myQueueCreate();* myQueuePush(obj, x);* int param_2 = myQueuePop(obj);* int param_3 = myQueuePeek(obj);* bool param_4 = myQueueEmpty(obj);* myQueueFree(obj);
*/另一种解法:
大家看了上面的解法之后,有没有一种感觉,就是这么做,好麻烦呀,要将栈的数据转移两次,每次都要转移两次,那这好麻烦,万一栈内数据庞大,那岂不是要给CPU干冒烟呀,是的,诸位,这是实话,确实是有可能,那么我们有没有什么方法,能够减少转移的次数呢?只需要转移一次就好了。
诶有的朋友,朋友有的,这就需要我们设置两个栈,一个栈负责被输入数据(我们叫pushst),一个栈负责删除数据(我们叫popst),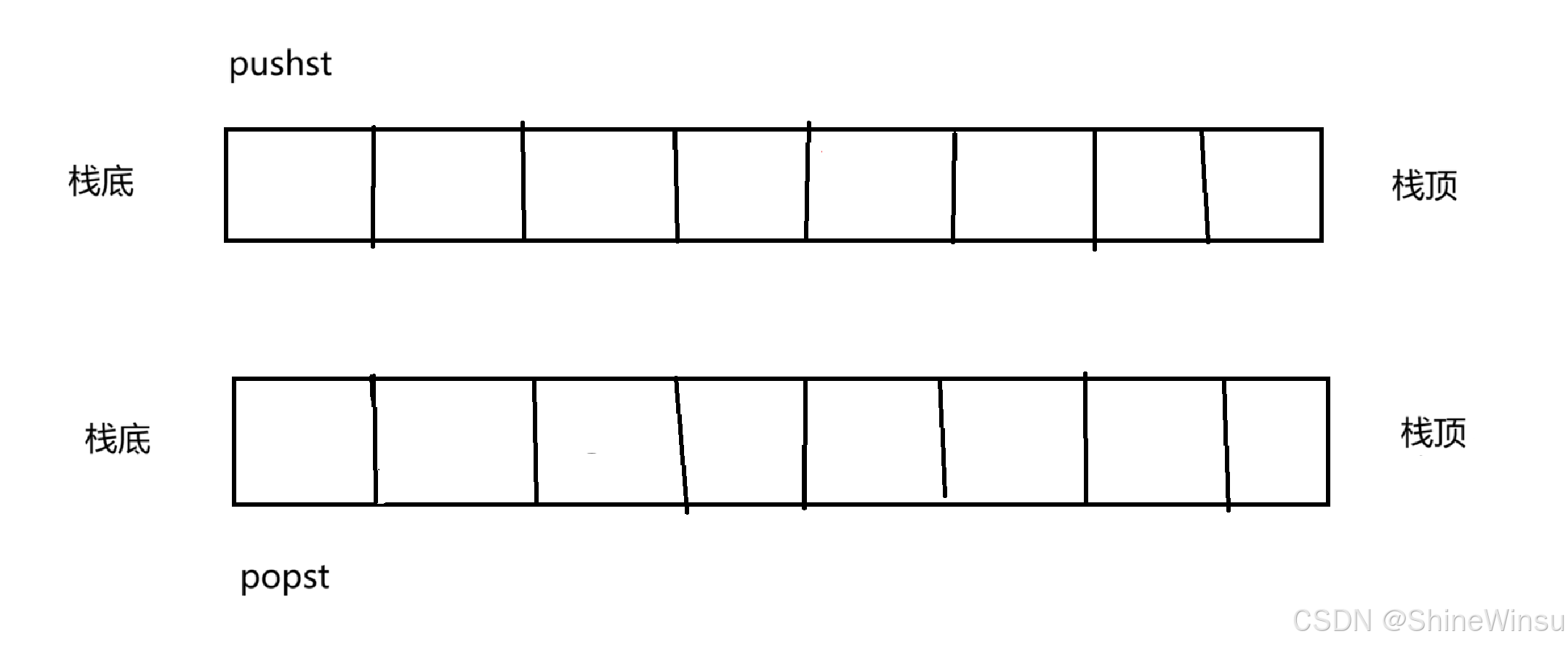
每当我们要插入新数据时,全部都往pushst中插入数据,坚决不往popst中插入数据,即如下图所示: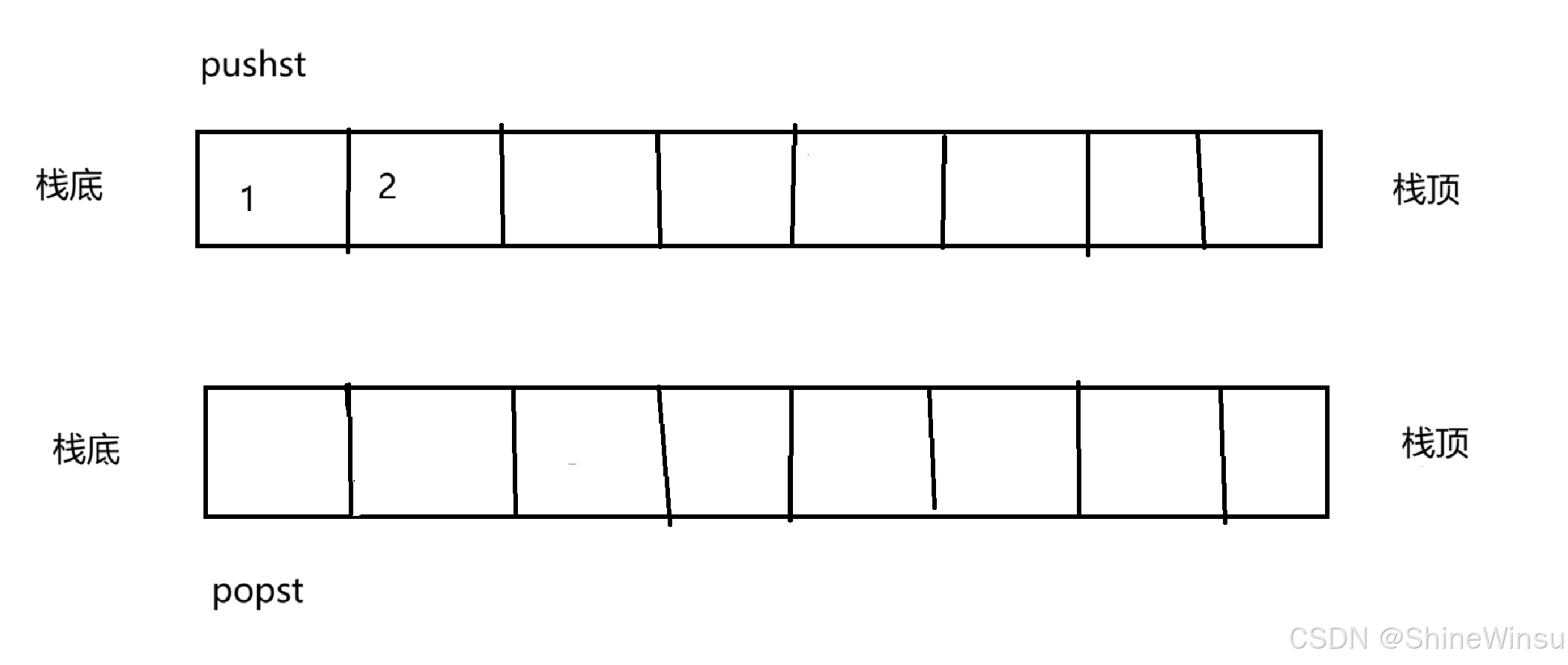
而每当我们要删除数据时,先看看popst中还有没有数据,如果没有数据的话,我们就从pushst中,通过尾取以及尾插,将pushst中的数据全部插入popst中,即如下图所示
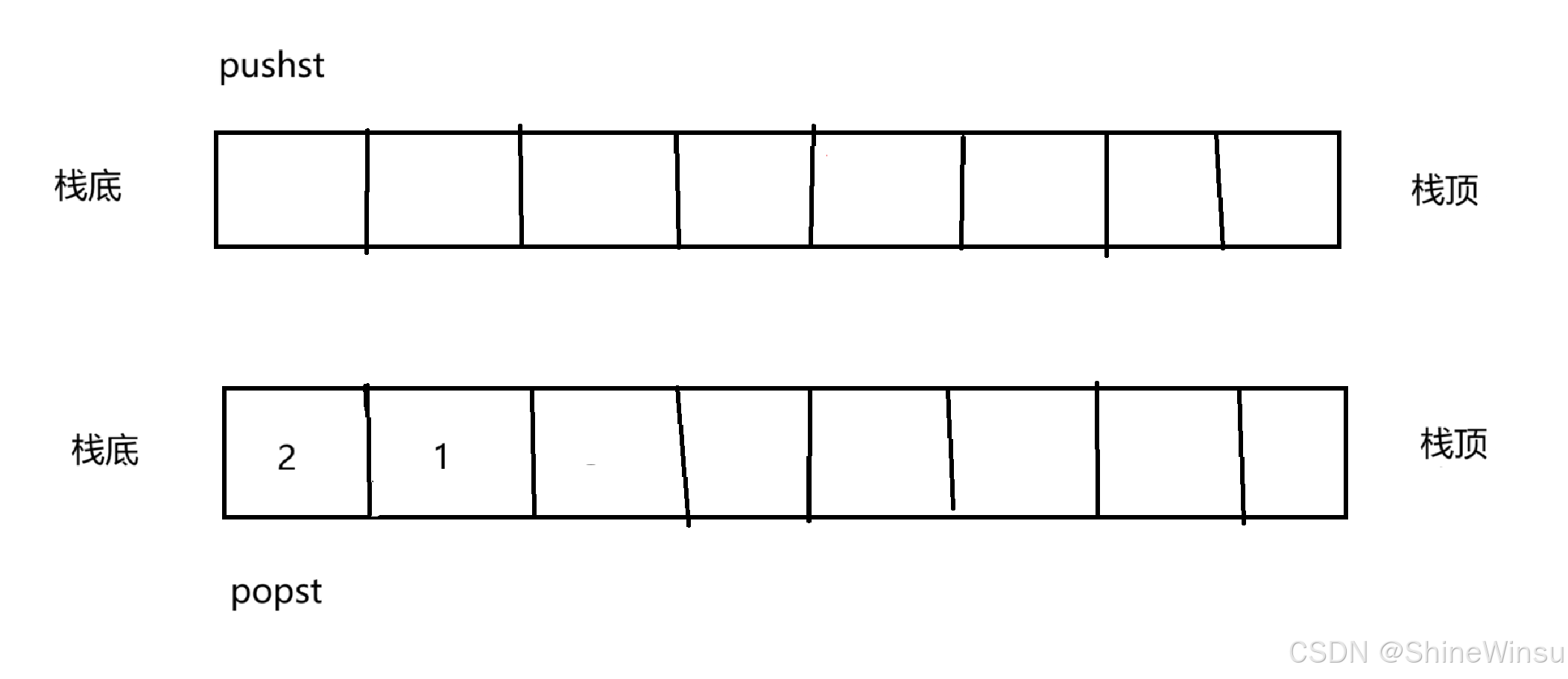
接下来在对popst进行尾删,这么一来,就可以实现队列的出队操作,即如下图
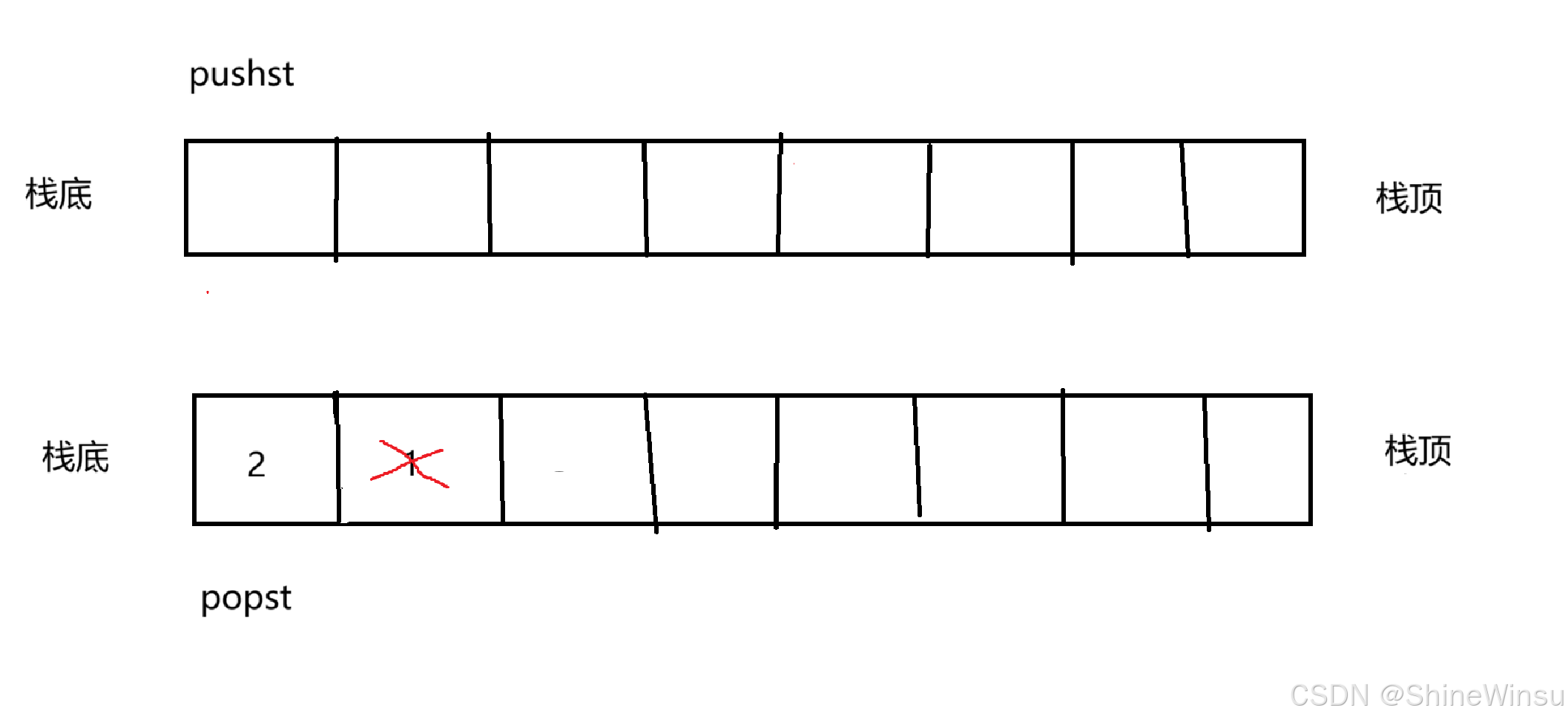
那么要是popst中,原本就有数据,那我们就不需要将pushst中的数据转移到popst中,因为如果popst中还有数据的话,是不是就代表着原队列的前几个数据还在popst中,而新插入的数据我们又是统一丢在pushst中,即如下图:
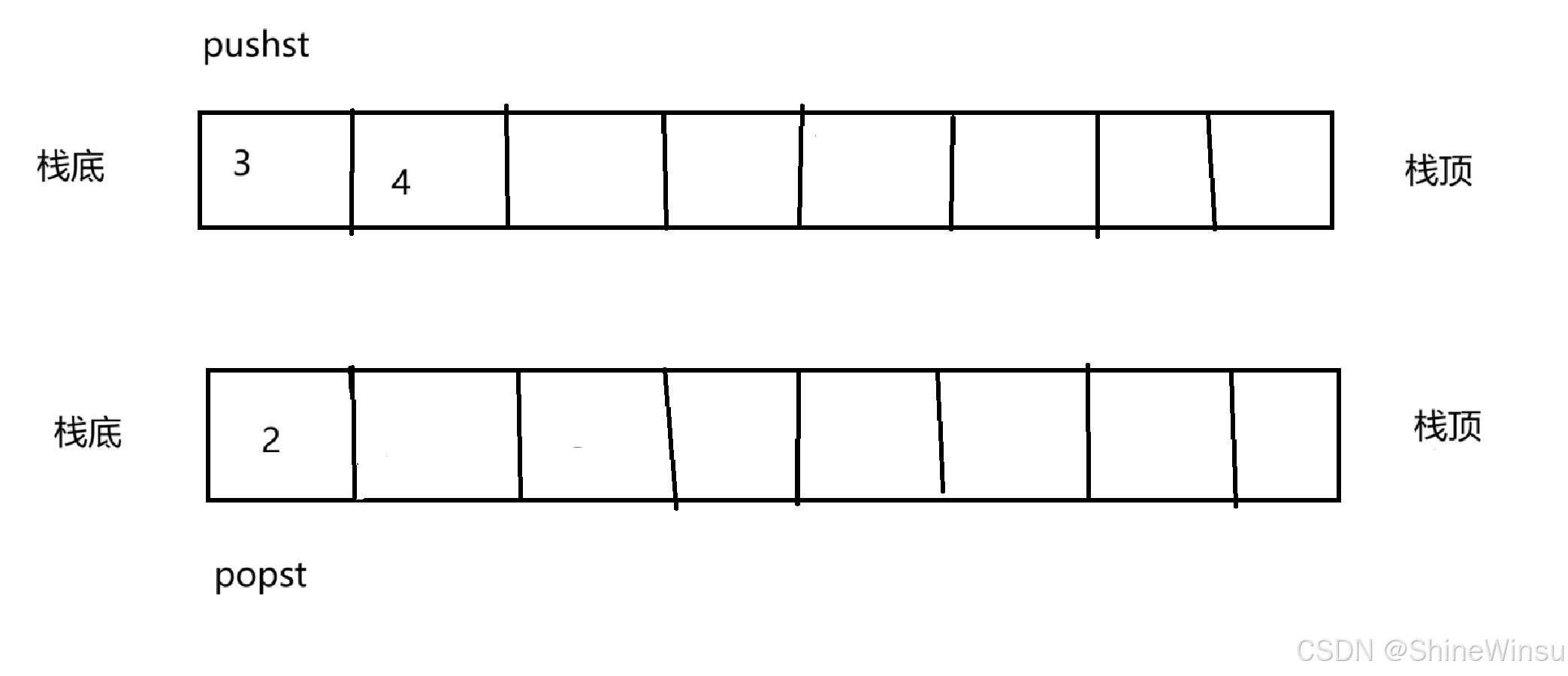
所以这么一来,我们就可以实现只用移动一次栈内的数据便能完成队列的出队操作。
至于我们要怎么取出队列的头元素呢,也很简单,就和上面的出队操作一样,只不过我们只取数据,并不删数据,所有大家这个能懂吧,一定要结合图去理解,最好自己画图理解理解,相信大家是一定能明白滴,聪明的大家~
那么到这边,我对这另一个解法,也就分析的差不多了,把这几个关键的操作给解决了,剩下的其他操作其实也就和上面说的那一个解法差不多了,大家自行理解以及书写代码,我在这里就直接给出完整代码供大家参考:
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>// 栈的结构体定义(顺序栈实现)
typedef int STDataType;
typedef struct Stack {STDataType* data; // 存储数据的数组int top; // 栈顶指针(指向栈顶元素的下一个位置)int capacity; // 栈的容量
} Stack;// 栈的初始化
void StackInit(Stack* ps) {assert(ps);ps->data = NULL;ps->top = 0;ps->capacity = 0;
}// 栈的销毁
void StackDestroy(Stack* ps) {assert(ps);free(ps->data);ps->data = NULL;ps->top = ps->capacity = 0;
}// 栈的扩容
void StackCheckCapacity(Stack* ps) {assert(ps);if (ps->top == ps->capacity) {int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* newData = (STDataType*)realloc(ps->data, newCapacity * sizeof(STDataType));if (newData == NULL) {perror("realloc failed");exit(1);}ps->data = newData;ps->capacity = newCapacity;}
}// 入栈操作(栈顶插入)
void StackPush(Stack* ps, STDataType x) {assert(ps);StackCheckCapacity(ps);ps->data[ps->top++] = x;
}// 出栈操作(栈顶删除)
void StackPop(Stack* ps) {assert(ps);assert(ps->top > 0);ps->top--;
}// 获取栈顶元素
STDataType StackTop(Stack* ps) {assert(ps);assert(ps->top > 0);return ps->data[ps->top - 1];
}// 判断栈是否为空
bool StackEmpty(Stack* ps) {assert(ps);return ps->top == 0;
}// 用两个栈实现队列的结构体
typedef struct {Stack pushst; // 负责接收数据的栈Stack popst; // 负责删除数据的栈
} MyQueue;// 队列初始化
MyQueue* myQueueCreate() {MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));if (q == NULL) {perror("malloc failed");exit(1);}StackInit(&q->pushst);StackInit(&q->popst);return q;
}// 队列的入队操作(尾插)
void myQueuePush(MyQueue* obj, int x) {assert(obj);// 所有新数据都入pushst栈StackPush(&obj->pushst, x);
}// 将pushst中的数据转移到popst(仅在popst为空时调用)
void TransferData(MyQueue* obj) {// 只有当popst为空时才转移数据if (StackEmpty(&obj->popst)) {// 将pushst中的所有元素转移到popstwhile (!StackEmpty(&obj->pushst)) {// 取出pushst的栈顶元素STDataType topVal = StackTop(&obj->pushst);StackPop(&obj->pushst);// 插入到popst的栈顶StackPush(&obj->popst, topVal);}}
}// 队列的出队操作(头删)
int myQueuePop(MyQueue* obj) {assert(obj);assert(!myQueueEmpty(obj)); // 队列不为空才能出队TransferData(obj); // 确保popst中有数据// 取出popst的栈顶元素(即队列的队头)int frontVal = StackTop(&obj->popst);StackPop(&obj->popst); // 删除popst的栈顶元素return frontVal;
}// 获取队列的队头元素
int myQueuePeek(MyQueue* obj) {assert(obj);assert(!myQueueEmpty(obj)); // 队列不为空才能获取队头TransferData(obj); // 确保popst中有数据// 返回popst的栈顶元素(即队列的队头)return StackTop(&obj->popst);
}// 判断队列是否为空
bool myQueueEmpty(MyQueue* obj) {assert(obj);// 两个栈都为空时,队列才为空return StackEmpty(&obj->pushst) && StackEmpty(&obj->popst);
}// 队列的销毁
void myQueueFree(MyQueue* obj) {assert(obj);// 先销毁两个栈StackDestroy(&obj->pushst);StackDestroy(&obj->popst);// 再释放队列结构体free(obj);
}结语:
当我们敲完最后一行 “用栈实现队列” 的优化解法代码,看着测试用例里 “队头元素”“出队元素” 的输出和预期完全一致时,或许会突然明白:数据结构的学习,从来不是一场 “追求实用” 的冲刺,而是一次 “理解本质” 的漫游。就像 “用队列实现栈” 和 “用栈实现队列” 这两道题,从实际开发角度看,它们确实有些 “画蛇添足”—— 没人会在项目里放着语言自带的栈或队列不用,偏要费力气用另一个结构去模拟。但正是这种 “刻意的冗余”,让我们跳出了 “只会调用 API” 的舒适区,真正摸到了栈和队列的核心特性。
还记得最开始分析 “用队列实现栈” 时,我们对着两个空队列发懵:明明队列只能头删、尾插,怎么才能模拟出栈的尾删?直到拿起笔,把 “1、2、3、4、5” 依次放进 q1,再把前 4 个元素转移到 q2,看着 q1 里剩下的 “5”,才突然顿悟 “哦,原来两个队列的作用,是一个存数据、一个当临时容器”。那个瞬间的通透,比直接看答案要深刻得多 —— 因为我们自己走过了 “困惑、尝试、碰壁、解惑” 的完整过程,而这个过程,恰恰是理解数据结构的关键。
后来到 “用栈实现队列”,难度又上了一个小台阶。最开始用 “两次转移” 的思路时,总担心 “转移完数据顺序会不会乱”,每次写完代码都要反复调试:第一次把 s1 的元素转移到 s2,顺序颠倒了;再把 s2 的元素转移回 s1,顺序又回来了,只是删掉了最开始的 “队头”。虽然能实现功能,但看着代码里重复的 “假设空栈、非空栈” 逻辑,又会忍不住想:能不能少转移一次?于是才有了 “分工明确” 的优化解法 ——pushst 只负责接收新数据,popst 只负责输出旧数据,只有当 popst 为空时才把 pushst 的元素转移过去。这个过程,其实是在训练我们 “从‘能实现’到‘更高效’” 的思维转变,而这种转变,会在后续学 “哈希表优化查找”“二叉树优化遍历” 时派上大用场。
我们在这两道题里反复强调的 “画图分析”,也不仅仅是一种解题技巧。当我们把 “队列转移数据”“栈颠倒顺序” 的过程画在纸上时,本质上是在把抽象的 “数据流动” 变成具象的 “步骤拆解”。就像面对 “用栈实现队列的头取操作” 时,光靠脑子想 “先转哪个栈、再转哪个栈” 很容易混乱,但画一张 “s1→s2 转移后栈顶是队头,取完再转回去” 的图,逻辑瞬间就清晰了。这种 “抽象问题具象化” 的能力,会伴随我们整个数据结构的学习之路 —— 无论是后续学链表的反转、树的层序遍历,还是图的深度优先搜索,画图永远是帮我们梳理思路的 “万能钥匙”。
还有一个容易被忽略的点,就是代码里那些 “细节”:比如用队列实现栈时,初始化结构体是用 “队列变量” 还是 “队列指针”,要不要额外申请内存;用栈实现队列时,栈的 top 是初始化为 0 还是 - 1,扩容时是设初始容量为 2 还是 4。这些看似琐碎的选择,其实藏着对 “内存管理” 和 “边界条件” 的考量。比如当初始化 MyStack 结构体时,直接用 que q1、que q2 这样的变量,就不用额外 malloc,而如果用 que* q1、que* q2 的指针,就必须记得申请内存再初始化 —— 这些细节没处理好,代码运行时就会出现 “野指针”“内存泄漏” 的问题。而正是在一次次处理这些细节的过程中,我们才慢慢养成了 “严谨写代码” 的习惯,这种习惯,比单纯会做某一道题更重要。
或许有朋友会觉得,学这些 “相互模拟” 的题目没什么用,不如直接学 “二叉树”“动态规划” 这些 “看起来更重要” 的内容。但其实,数据结构的知识就像一串链条,栈和队列是最基础的一环,它们的 “后进先出”“先进先出” 特性,会在后续很多场景里反复出现:比如二叉树的深度优先遍历要用栈,广度优先遍历要用队列;比如解决 “括号匹配”“每日温度” 问题要用单调栈;比如处理 “生产者 - 消费者模型” 要用阻塞队列。今天我们花时间把栈和队列的本质吃透,后续学更复杂的结构时,就会像 “搭积木” 一样轻松 —— 因为那些复杂结构的底层,往往藏着我们今天反复琢磨的基础逻辑。
最后想跟大家说,数据结构的学习从来没有 “捷径”。可能我们今天对着 “两个栈怎么模拟队列” 想了半小时还没思路,可能我们写代码时因为 “忘记转移数据后更新栈顶指针” 调试了好久,可能我们甚至会怀疑 “我是不是不适合学这个”。但请别着急,每一次困惑都是进步的起点,每一次调试都是经验的积累。就像我们今天从 “不会” 到 “会”,从 “两次转移” 到 “一次优化”,这个过程本身就是成长。
接下来,我们会带着今天学到的 “栈与队列” 的知识,去探索更广阔的领域:比如能快速找到最大值的 “单调栈”,能实现 “先进先出” 且支持优先级的 “优先队列”,还有结合了栈和队列特性的 “双端队列”。每一个新结构都是对旧知识的延伸,每一次新探索都是对逻辑思维的锤炼。愿我们都能保持这份 “琢磨细节” 的耐心,在数据结构的世界里,一步一个脚印地走下去,把每一个基础都打牢,把每一个逻辑都想透 —— 相信到最后,我们不仅能写出优雅的代码,更能拥有一套 “解决复杂问题” 的清晰思路。咱们下次探索之旅,再见!
