电容的串联、并联
1.电容、电感串联、并联
| 电容 | 电感 | |
| 串联 | 相当于电阻并联 | 相当于电阻串联 |
| C1与C2串联:C=(C1*C2)/ (C1+C2) | L1与L2串联:L=L1+L2 | |
| 并联 | 相当于电阻串联 | 相当于电阻并联 |
| C1与C2并联:C=C1+C2 | L1与L2串联:L=(L1*L2)/ (L1+L2) |

口诀: “电感串并,规律同电阻;电容串并,规律恰相反。”
电容串联、并联
核心概念对比
| 特性 | 并联 | 串联 |
|---|---|---|
| 定义 | 所有电容器的两端分别直接连接在一起 | 电容器首尾相连,形成一个链状 |
| 电路图 | ─┬─[C1]─┬─ ─┼─[C2]─┼─ ─┴─[C3]─┴─ | ───[C1]───[C2]───[C3]─── |
| 总电容 | 增大 Ctotal=C1+C2+⋯+Cn | 减小 1Ctotal=1C1+1C2+⋯+1Cn |
| 电压 | 每个电容器两端电压相等,等于电源电压 | 每个电容器分压,总和等于电源电压 Vtotal=V1+V2+⋯+Vn |
| 电荷量 | 每个电容器存储的电荷量不同 Qtotal=Q1+Q2+⋯+Qn | 流过每个电容器的电荷量相同 Q=C1V1=C2V2=⋯ |
| 作用 | 增加系统总电容,提高储能能力 | 提高系统总耐压,降低总电容 |
一、电容器并联
1. 总电容计算
当电容器并联时,相当于增加了电容板的极板面积。根据电容公式 C=εA/d,面积A增大,电容C也随之增大。ε为介电常数
公式:
Ctotal=C1+C2+C3+⋯+Cn
结论:并联后的总电容是所有单个电容之和。
2. 电压关系
所有电容器的两个极板都直接连接到电源的两端,因此它们两端的电压完全相同。
Vtotal=V1=V2=V3=⋯=Vn
3. 电荷量关系
根据 Q=C×V由于电压V相同,但电容C不同,因此每个电容器存储的电荷量也不同。电容越大的,存储的电荷越多。
Q1=C1V,Q2=C2V,⋯
总电荷量为各电容器电荷量之和:
Qtotal=Q1+Q2+⋯+Qn=(C1+C2+⋯+Cn)V
简单比喻: 并联就像把几个一样大的水桶并排放在一起,它们的水面高度(电压)总是相同的。往这个系统里加水(充电),水会按每个桶的底面积(电容)大小分配到各个桶中。总储水量(总电荷)是所有桶的储水量之和。
二、电容器串联
1. 总电容计算
当电容器串联时,相当于增加了电容板之间的距离d。根据电容公式 C=εA/d,距离d增大,电容C减小。
公式:
1/Ctotal=1/C1+1/C2+1/C3+⋯+1/Cn
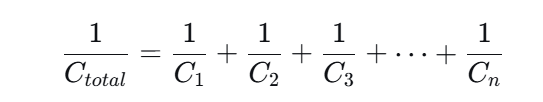
对于两个电容串联的常见情况,公式可简化为:
Ctotal=(C1×C2)/(C1+C2)
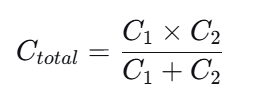
结论:串联后的总电容小于任何一个单独的电容。
2. 电荷量关系
在串联电路中,电流路径只有一条。当电源对电路充电时,同一大小的电流会依次流过所有电容器,因此在同一时间内,每个电容器极板上积累的电荷量Q是完全相同的。
Qtotal=Q1=Q2=Q3=⋯=Qn
3. 电压关系
根据 V=Q/C,由于电荷量Q相同,但电容C不同,因此每个电容器两端的电压也不同。电容越小的,因其存储电荷能力弱,分担的电压就越高。
V1=Q/C1,V2=Q/C2,⋯
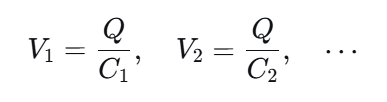
总电压为各电容器电压之和:
Vtotal=V1+V2+⋯+Vn=Q(1/C1+1/C2+⋯+1/Cn)
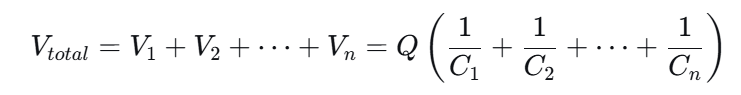
重要警示: 在串联电路中,如果各个电容器的容量不同,小容量的电容器会因为分担过高的电压而存在被击穿的风险。一旦其中一个被击穿(相当于短路),全部电源电压将加在其余电容器上,可能导致连锁击穿。
简单比喻: 串联就像几个直径相同但长度不同的弹簧首尾相接。当你拉动整个弹簧串时,每个弹簧的伸长量(电压)不同,劲度系数越大(电容越大)的弹簧伸长越小。但作用于整个串联系统的力(电荷)是相同的。
三、工程应用举例
并联应用:提高容量和储能
超级电容模组:通过将多个超级电容并联,可以获得巨大的总电容量,用于短时大功率放电或能量回收。
电源滤波:在直流电源电路中,并联一个大电容和一个小电容,可以分别滤除低频和高频噪声。
串联应用:提高耐压
高压电力电容器:单个电容器的耐压有限。通过将多个电容器串联,可以承受更高的系统电压。例如,在输电线路上用于无功补偿的串联电容器组。
电容分压器:利用串联电容的分压原理,可以测量高电压。
总结: 选择并联还是串联,取决于你的需求。需要大容量——用并联;需要高耐压——用串联。
电感串联、并联
核心概念对比
| 特性 | 串联 | 并联 |
|---|---|---|
| 定义 | 电感器首尾相连,形成一个链状 | 所有电感器的两端分别直接连接在一起 |
| 电路图 | ───[L1]───[L2]───[L3]─── | ─┬─[L1]─┬─ ─┼─[L2]─┼─ ─┴─[L3]─┴─ |
| 总电感 | 增大 Ltotal=L1+L2+⋯+Ln | 减小 1/Ltotal=1/L1+1/L2+⋯+1/Ln |
| 电流 | 流过每个电感的电流相同 | 每个电感分流,总和等于总电流 Itotal=I1+I2+⋯+In |
| 电压 | 每个电感分压,总和等于电源电压 Vtotal=V1+V2+⋯+Vn | 每个电感两端电压相等,等于电源电压 |
| 作用 | 获得更大的电感值 | 获得更小的电感值,或承受更大的电流 |
一、电感串联
1. 总电感计算
当电感器串联时,相当于增加了线圈的总长度。根据电感公式 如下,匝数N增加(或长度l增加),电感L增大。由于电流路径唯一,磁场相互增强。
电感公式:
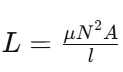
公式:
Ltotal=L1+L2+L3+⋯+Ln
结论:串联后的总电感等于所有单个电感之和。
前提是电感之间没有磁耦合(即彼此的磁场不相互影响)。如果存在耦合,计算会复杂得多。
2. 电流关系
在串联电路中,电流路径只有一条,因此流过每一个电感的电流完全相同,且等于总电流。
Itotal=I1=I2=I3=⋯=In
3. 电压关系
根据电感的电压公式 ,由于电流变化率 di/dt 相同,但电感L不同,因此每个电感两端的电压也不同。电感值越大的,其两端产生的感应电压就越高。
电感的电压公式:
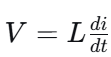
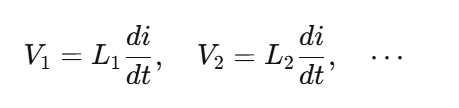
总电压为各电感电压之和:
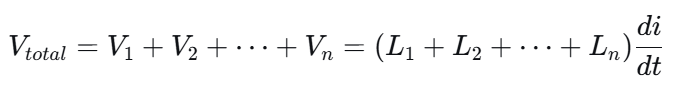
简单比喻: 串联就像几个人排成一队合力拉一根绳子,每个人的拉力(电流)必须相同,但每个人使出的力气(产生的电压降)可以不同。总阻力(总电感)是所有人阻力的总和。
二、电感器并联
1. 总电感计算
当电感器并联时,相当于提供了多条并行的电流路径。根据电感公式,这可以被理解为等效截面积的增加。总的电感值会减小。
公式:
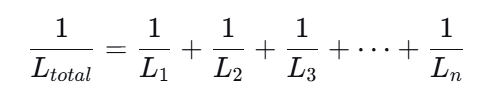
对于两个电感并联的常见情况,公式可简化为:
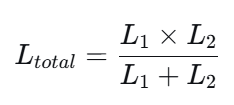
结论:并联后的总电感小于任何一个单独的电感。
同样,前提是电感之间没有磁耦合。
2. 电压关系
所有电感器的两端都直接连接到电源的两端,因此它们两端的电压完全相同。
Vtotal=V1=V2=V3=⋯=Vn
3. 电流关系
根据 如下公式,可以推导出在电压相同的情况下,电流的变化率 di/dt 与电感L成反比。在稳态直流或交流有效值分析中,这意味着电感值越小的支路,分得的电流越大。
公式:
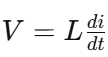
总电流为各支路电流之和:
Itotal=I1+I2+⋯+In
重要提示: 在并联电路中,如果突然断开开关,电感值大的支路会因为电流不能突变而产生很高的感应电压,需要设计续流回路(如二极管)以防止损坏电路。
简单比喻: 并联就像几条宽度不同的河道并行通向大海。各河道的水面高度(电压)是相同的,但宽的河道(电感小)流过的水流(电流)更大。总的水流能力(总电感的倒数)是所有河道水流能力之和。
三、工程应用举例
串联应用:获得大电感
滤波电路:在开关电源的输出端,有时会串联多个电感以获得更大的电感量,从而实现更好的滤波效果,减小输出纹波。
阻抗匹配:在射频电路中,通过串联电感来调整电路的阻抗。
并联应用:获得小电感或分流大电流
大电流应用:当单个电感的额定电流不足以承受电路总电流时,可以将多个电感并联使用,以分担电流。
高频电路:在需要很小电感值的场合,并联是一种方便的实现方式。
总结: 选择串联还是并联,取决于你的需求。需要大电感值——用串联;需要小电感值或分流大电流——用并联。 同时,务必注意电感之间应尽量避免不必要的磁耦合,否则会严重影响电路性能。
