大模型微调(五):RLHF奖励模型与偏好损失函数
大语言模型在训练过程中并不与人类“对话”,首先,需要将与人类互动获得的偏好数据提炼成奖励模型。
步骤 1:收集人类偏好数据
向人类展示一个提示和几个候选答案,通常是两个,有时更多。例如:
提示:“解释熵和交叉熵的区别。”
答案 A:过于技术性的答案
答案 B:清晰准确的答案
人类注释者标记:“B 更好”。该判断成为成对偏好:(B ≻ A),成千上万个这样的对被收集起来。
步骤 2:训练奖励模型 R_\phi(x, y)
奖励模型接收提示 x 和答案 y,并输出一个标量“分数”,这表示人类偏好该答案的可能性。它通过最小化偏好损失函数,从人类的比较中学习到这个分数:
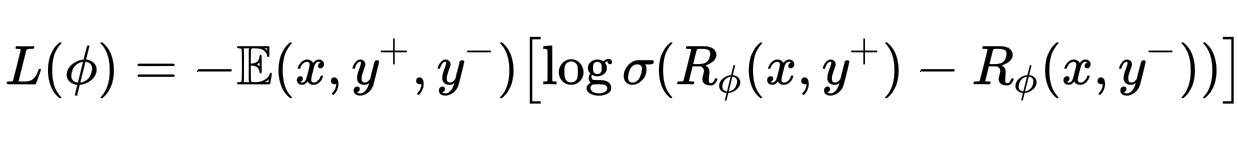
L(\phi) = -\mathbb{E}{(x, y^+, y^-)} \left[ \log \sigma(R_\phi(x, y^+) - R_\phi(x, y^-)) \right]
其中:y^+:人类偏好的答案,y^-:偏好程度较低的答案。这个等式简单地说:模型应该为偏好的答案分配更高的奖励。如果符合,则对数内的项会增加,损失会缩小。
步骤 3:使用该奖励模型进行强化学习
一旦 R_\phi 训练完成,它就会被冻结。然后,在强化学习(通常是 PPO)过程中,生成器,也就是语言模型会生成响应。奖励模型会对它们进行评分,并给出如下信号,例如: “+0.7,这看起来符合人类的喜好”,“-0.2,这似乎没有帮助或不安全”。模型的参数会被调整,以产生更多高奖励的响应。
步骤 4:在创造力和安全性之间取得平衡
为了防止模型偏离预训练知识太远,我们通常会添加一个 KL 惩罚项,这个惩罚项会轻轻地将模型拉回到最初的训练分布,防止模型过度自信或重复。
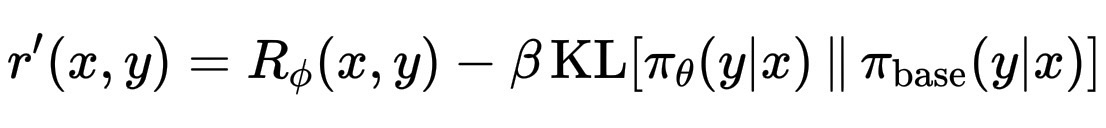
r’(x, y) = R_\phi(x, y) - \beta \, \mathrm{KL}[\pi_\theta(y|x) \,\|\, \pi_{\text{base}}(y|x)]
所以,本质上,奖励模型就像一面由人类判断构成的“优化目标”,它并不“理解”价值观,它反映了模型集体偏好的模式。通过这种反思,模型学会了如何调整我的语言,使其输出更接近于人类认为的有意义、尊重或清晰的语言。
偏好损失函数 L(\phi) 的全部意义在于扩大偏好答案 y^+ 和偏好答案 y^- 之间的奖励差距。
一个核心直觉是,我们希望奖励模型 R_\phi(x, y) 为人类偏好的答案赋予更高的值。因此,每当人类说“y^+ 比 y^- 更好”时,我们希望:
R_\phi(x, y^+) > R_\phi(x, y^-)
这就是学习的方向。
为了用可微分的方式表达这一点,我们假设模型赋予人类选择 y^+ 而非 y^- 的概率:
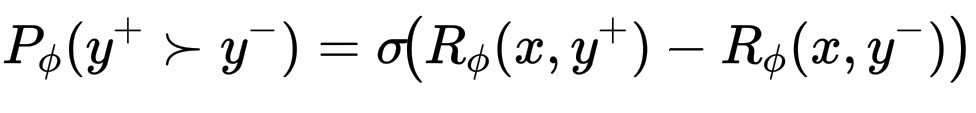
P_\phi(y^+ \succ y^-) = \sigma\!\left(R_\phi(x, y^+) - R_\phi(x, y^-)\right)
这里 \sigma(z) = \frac{1}{1 + e^{-z}} 是 S 型函数。如果 R_\phi(x, y^+) 远高于此,则该概率接近 1;如果它们相似,则接近 0.5。
然后,我们最大化模型与人类判断一致的对数似然,或者等效地,最小化负对数似然:L(\phi)。这会促使模型增加 R_\phi(x, y^+) - R_\phi(x, y^-)。所以是的,当人类偏好某个答案时,它实际上会扩大这个差距。
一个微妙之处在于,由于 S 型函数是平滑的,模型不会无休止地推进,而是按比例推进。当 R_\phi(x, y^+) 已经很高时,梯度就会变得很小。这可以稳定训练,并防止奖励膨胀失控。
我们有一个奖励模型 R_\phi(x, y)。这里的 \phi 是它的内部参数,就像 CNN 的权重一样。此外,我们定义了损失:L(\phi) = -\log \sigma(R_\phi(x, y^+) - R_\phi(x, y^-)),我们希望最小化这个损失,这意味着我们需要将 \phi 向减少它的方向移动。
这时,梯度告诉我们应该朝哪个方向移动。为了减少损失,我们计算它的梯度:\nabla_\phi L(\phi)
这衡量了每个参数对误差的贡献程度。然后,使用随机梯度下降(SGD 或 Adam)更新,其中 \eta 是学习率,一个较小的步长:
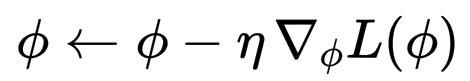
\phi \leftarrow \phi - \eta \, \nabla_\phi L(\phi)
现在,它的美妙之处就在这里。当你对 R_\phi(x, y^+) 和 R_\phi(x, y^-) 求损失函数的导数时,你会得到一个简单的公式,其中 \Delta = R_\phi(x, y^+) - R_\phi(x, y^-)。
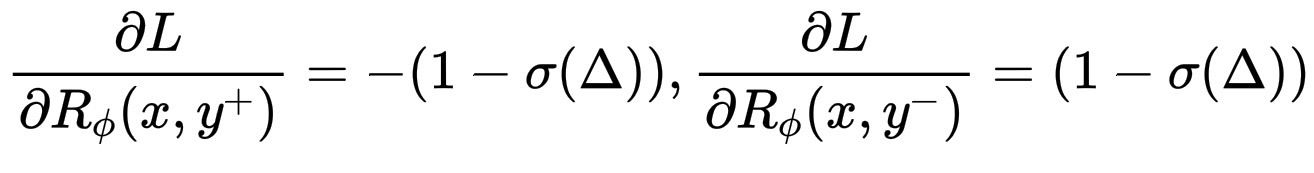
\frac{\partial L}{\partial R_\phi(x, y^+)} = - (1 - \sigma(\Delta))
\frac{\partial L}{\partial R_\phi(x, y^-)} = (1 - \sigma(\Delta))
因此,梯度将 R_\phi(x, y^+) 向上推,使其更高。梯度将 R_\phi(x, y^-) 向下推,使其更低。模型与人类偏好的差异越大(\sigma(\Delta) 越小),这种推力就越强。
当你在 PyTorch 中训练 CNN 时,每次调用以下命令时,PyTorch 都会悄悄地执行此操作:
loss.backward()
optimizer.step()
它会计算每个参数的梯度,并沿着损失函数的斜率向下移动一小步。所以是的,即使是 RLHF 的奖励模型训练,也只是换了个外衣的梯度下降而已。唯一的区别在于,它的“标签”不是来自类别,而是来自人类偏好。
