基于多焦点高斯邻域注意力机制与大规模基准的视频人群定位

摘要

视频人群定位是一项关键但极具挑战性的任务，其目标是估计给定拥挤视频中人头的精确位置。为了对人类移动的时空依赖性进行建模，我们提出了一种多焦点高斯邻域注意力机制（GNA），该机制能够有效地利用长距离对应关系，同时保持输入视频的空间拓扑结构。特别是，我们配备的多焦点机制使GNA能够很好地捕捉人头的尺度变化。基于多焦点GNA，我们开发了一个统一的神经网络，称为GNANet，它通过场景建模模块和上下文交叉注意力模块，充分聚合时空信息，从而在视频片段中精确定位人头中心。此外，为了促进该领域的未来研究，我们引入了一个名为VSCrowd的大规模人群视频基准，该基准包含在各种监控场景中捕获的60,000多帧图像和200多万个人头标注。最后，我们在包括我们提出的VSCrowd在内的三个数据集上进行了广泛的实验，实验结果表明，所提出的方法在视频人群定位和计数方面均能达到最先进的性能。

索引词—视频人群分析，高斯邻域注意力，VSCrowd数据集，时空建模

I. 引言

基于监控的人群分析[1], [2], [3]因其在公共安全中的重要应用而在学术界和工业界引起了广泛关注。在过去的十年中，众多模型[4], [5], [6], [7], [8], [9], [10], [11], [12]被提出用于人群计数，但它们大多只生成粗略的密度图，其总和即为计数。尽管这些方法在人群计数方面取得了优异的性能，但它们无法获得人头的准确位置，这限制了它们在许多更精细、更有价值的下游任务（如人群跟踪和人群预测）中的应用。例如，人群跟踪需要任意历史时刻所有人的精确位置来恢复视频序列中人的轨迹。这些任务对公共安全至关重要。

然而，大多数人群计数方法生成的粗略密度图仅反映人群的空间分布，对于上述下游任务而言是不够的。受此启发，我们聚焦于一个更基础但更具挑战性的任务——人群定位，其目标是在无约束场景中自动定位各种尺度的人头。

直观上，人群定位可以被建模为人头检测，并使用常见的目标检测框架来解决，例如单阶段检测器（FCOS[13]、YOLO[14]等）和两阶段检测器（Faster-RCNN[15]、RFCN[16]等）。然而，这些检测方法无法处理人头通常非常微小且相互重叠的极端拥挤场景[17]。至于特定的人脸检测方法[18], [19]，它们只关注朝向摄像头的脸部，而人群定位旨在定位人群中各种朝向的所有人头（包括极小的人头）。因此，人头检测的精度和召回率在人群分析中并不理想[20], [21]。在这种情况下，我们通过直接预测人头中心的位置来解决人群定位问题。与检测方法获取人头的完整边界框不同，我们的方法仅旨在找到它们的位置，并给出基于关键点的预测（如果未重叠则为人头中心，如果重叠则为可见部分的中心）。在这种情况下，我们的方法对重叠的人头更具鲁棒性，因为我们不必找到完整的人头，只需部分人头就足以进行预测。

现有的人头分析方法大多基于单张图像，即使用静态图像来估计计数和定位结果[22], [23], [2], [25]。由于仅利用了空间信息，这些方法通常在远处或模糊区域会出现严重的误检和漏检问题。尽管一些近期的方法利用了时间信息[26], [27], [28]，但它们仅解决了视频中的人群计数问题，而未考虑人头的位置。我们认为，结合相邻帧的时间信息对于发现人头的困难样本至关重要。为此，我们提出在视频而非图像上解决人群定位问题。具体来说，我们的目标是通过同时考虑目标帧的相邻帧来改善目标帧的定位结果。

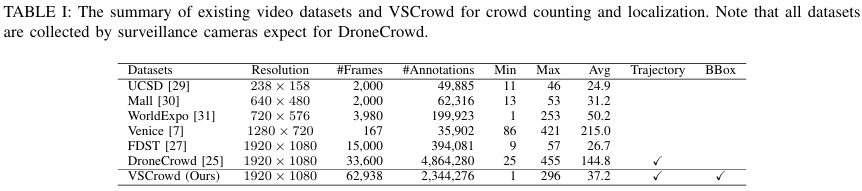
最近，主流的人群分析方法通常依赖于卷积神经网络，其训练需要大规模的标注数据。然而，现有的人头数据集要么专注于单图像分析，要么规模较小。表I总结了常用的人群计数和定位视频基准。我们可以看到，UCSD[29]、Mall[30]、WorldExpo[31]、Venice[7]和FDST[27]包含的帧数和标注数量都很少，这限制了深度模型的泛化能力。至于近期的DroneCrowd数据集[25]，它是通过无人机视角的摄像头捕获的。尽管DroneCrowd覆盖了更广阔的场景，但个体的细节并未保留。除了表I中的数据集外，还存在其他记录行人的视频数据集，如CrowdFlow[32]、DukeMTMC[33]和PETS2009[34]，但它们专注于不同的任务，无法直接应用于主流的人群分析。例如，CrowdFlow是一个移动个体光流数据集，包含由虚幻引擎合成的高清视频；DukeMTMC是一个大规模、高质量的监控数据集，带有边界框标注，广泛用于跟踪、重识别和人脸识别，但由于其中的人数不足，无法用于人群分析。因此，一个具有代表性的监控视角基准对于视频人群定位研究至关重要。为了促进该任务的研究，我们创建了一个名为VSCrowd的大规模视频数据集。该数据集包含62,938帧高分辨率的监控视角图像，并对2,344,276名行人进行了标注。除了人头中心的点标注外，我们还为每个实例提供了有价值的边界框和轨迹。值得注意的是，我们的视频帧是在各种场景（如商场、街道、景点）中捕获的，如图1所示。总而言之，VSCrowd在可扩展性、多样性、难度和应用性方面都是一项重大贡献。

直观上，时空依赖性对于视频人群定位至关重要。最近，注意力机制因其在捕捉全局依赖性方面的强大能力而在各个领域取得了巨大成功[35], [36], [37], [38], [39]。受此启发，我们也采用注意力机制来建模时空特征之间的对应关系。然而，传统的注意力机制（即全注意力）存在两个局限性：1) 其相对于序列长度的二次方时间和内存复杂度严重限制了模型处理长序列的能力[40], [41]；2) 在计算注意力时可能会引入不必要和冗余的信息[42]。为了克服这些缺点，我们提出了高斯邻域注意力（GNA），它从以查询位置为中心的高斯分布邻域中采样固定数量的键。与全注意力不同，GNA可以在捕捉长距离依赖的同时保持数据的空间拓扑结构。此外，我们为GNA配备了多焦点机制，该机制采样并聚合不同高斯范围内的注意力特征，以处理由透视效应引起的人头尺度变化。我们还从理论上证明了所提出的多焦点注意力机制能够捕捉数据内的长距离依赖。

基于多焦点GNA，我们开发了一个用于视频人群定位的统一框架，称为GNANet。它充分学习时空相关性，以定位人群视频片段中目标帧（即中间帧）的行人。具体来说，GNANet首先从视频片段中的每一帧分别提取语义特征，然后聚合这些特征以建模整个片段的场景上下文。通过将计算出的场景上下文视为查询，上下文交叉注意力模块利用两种键源来捕捉视频的时空信息，即目标帧的特征和所有帧的特征。特别地，设计了一个目标帧交叉注意力来捕捉目标帧内人头像素之间的空间依赖性，而时间交叉注意力则用于相邻帧像素之间的相关性。通过这种方式，时间信息被聚合到目标帧中以实现更好的定位。最后，将注意力输出与目标帧的特征相结合，以预测定位图。

本文的贡献总结如下：

• 创建了一个用于人群定位的大规模监控视频数据集。该数据集包含634个视频（62,938帧）和2,344,276个标注，全面覆盖了各种人群场景。
• 提出了多焦点高斯邻域注意力（GNA），用于捕捉局部依赖和长距离依赖，并通过不同感受野大小的特征图进行人头尺度建模。
• 我们开发了一种基于GNA的网络用于视频人群定位，其中利用场景建模和上下文交叉注意力分别保留片段信息和建模时空相关性。所提出的网络在多个数据集上实现了最先进的定位性能和相当的计数精度。

本文其余部分组织如下。我们在第二节回顾了关于人群分析和注意力机制的一些相关工作。第三节提出了一个大规模的监控视角视频人群数据集（VSCrowd）。然后，在第四节详细阐述了用于视频人群定位的新颖框架。为了证明我们方法的有效性，我们在第五节进行了广泛的实验，包括与现有方法的比较、消融研究和进一步分析。最后，我们在第六节做出了一些结论。

II. 相关工作

A. 人群计数与定位

1. 单图像人群计数。先前关于人群分析的工作主要集中在人群计数上，即估计人群图像中人的总数[43], [44], [45], [46], [47], [9], [5], [48], [49], [50], [51], [52]。近年来提出了许多单图像人群计数方法。首次在[53]中将人群计数表述为密度图回归。此外，考虑到由于透视效应或图像分辨率导致的人头大小变化，开发了一种多列卷积神经网络（MCNN）架构，将人群图像映射到其人群密度图。与多尺度架构不同，CSRNet[45]由一个用于特征提取的卷积神经网络（CNN）和一个用于密度图回归的扩张CNN组成。通过用扩张卷积核替换池化操作，获得了更大的感受野。受CSRNet中扩张卷积的启发，自适应扩张卷积被提出并用于人群计数[47]。此外，提出了自校正（SC）监督，通过迭代校正标注并优化模型来同时考虑整体和个体。为了解决透视效应引起的人头大小变化，PGCNet[9]使用透视信息来指导特征图的空间变化平滑，其中透视信息由一个专门设计的分支进行估计。在[7]中提出了上下文感知的人群计数，该方法提取多个感受野大小的特征，并学习特征的位置重要性。与基于密度图估计的方法不同，贝叶斯损失[54]使用点标注来构建密度贡献概率模型。实验表明，使用贝叶斯损失训练的标准骨干网络在很大程度上优于使用基线损失训练的网络。纯人群计数方法通常生成一个密度图，其总和即为图像中的人数。虽然这类方法无法提供个体的精确位置，但它们在网络结构方面具有启发性：比如CSRNet，我们使用编码器-解码器风格的框架来提取语义表示并预测定位图。

2. 单图像人群定位。尽管最先进的群体计数方法可以以较低的误差估计图像中的人数，但它们无法预测人头的确切位置。为了克服群体计数的这一局限性，近期的研究也考虑了群体定位，并提出了一些用于计数和定位的多任务方法[24], [22], [23]。与CSRNet类似，RAZNet[24]首先从群体图像中提取特征，然后通过两个分支分别预测密度图和定位图。此外，为了处理高密度区域，RAZNet中设计了一种检测与缩放策略。Idrees等人[55]提出在一个统一的框架中同时解决群体计数、密度图估计和定位问题，该框架由多个分支组成，每个分支负责生成具有特定锐度程度的密度图。D2C[51]将密度图估计分解为两个阶段：概率图回归和计数图回归。此外，在局部计数的指导下，提出了一种峰值点检测算法来定位人头中心。在[56]中提出了一种拓扑约束，使模型能够学习预测人头中心的空间排列。具体来说，基于持久同源理论，定义了一个持久性损失来比较真实标签和似然图地形景观的拓扑结构。在[57]中提出了一种广义损失函数来训练群体计数网络。已经证明，像素级$L_2$损失和贝叶斯损失是广义损失的特殊情况。由于预测的密度被推向人头中心，因此可以通过简单的后处理轻松获得定位图。P2PNet[58]被开发出来直接预测图像中的人头中心。利用匈牙利算法在预测点和真实点之间执行一对一匹配，然后根据匹配的点计算损失。最近也探索了一些基于检测的群体计数和定位方法。PSDDN[22]首先初始化伪真实边界框来训练检测器。然后设计了一种在线更新方案在训练过程中修改伪标注。类似地，在LSC-CNN[23]中开发了一种复杂的方案来生成伪真实边界框。然后在LSC-CNN中利用多列架构（配备自上而下的特征调制）来聚合多尺度特征图并在多个分辨率下进行预测。基于检测的方法不仅可以预测人头的确切位置，还可以预测其尺度。最先进的方法通常将此任务建模为微小目标检测，这需要伪边界框进行训练。这些伪边界框是根据标注点之间的几何距离估计的，因此其质量无法保证。在这种情况下，我们提出直接从帧中估计二值定位图。

3. 视频人群计数。为了进一步提高人群分析的性能，一些研究人员倾向于关注视频人群计数，即利用时空信息进行人数统计[26], [27], [28], [25]。双向ConvLSTM被用于捕捉视频序列中的空间和长距离时间依赖性[26]。在[27]中提出了局部约束空间变换网络（LSTN），其中LST模块利用当前帧的密度图来估计下一帧的密度图。此外，在这项工作中提出了一个用于视频人群计数的数据集（FDST）。在[28]中，通过估计人群流并求和来获得人群密度，并施加守恒约束以提高鲁棒性。Liu等人[59]提出估计帧间的人群流，并基于该流预测人群密度。与单图像人群计数相比，这种方法可以施加编码相邻帧之间时间依赖性的约束。与RAZNet的双分支架构类似，STANet被提出用于在[25]中使用帧序列进行人群计数和定位。在STANet中，连续帧的多尺度特征图被聚合以预测当前帧的密度图和定位图。尽管我们的工作和STANet解决了类似的问题，但我们有不同的动机和新颖的贡献：a) 我们处理的场景大不相同。具体来说，DroneCrowd由无人机捕获的视频组成，因此人的尺度很小但一致。相比之下，VSCrowd中的视频是监控视频，由于强烈的透视效应，人头的变化很大。与记录大面积全局动态的无人机视角视频相比，监控视频提供了拥挤地点的更多局部细节，我们希望利用这些细节进行细粒度的视频分析。b) 在STANet中，通过简单地组合相邻帧的特征图来利用时间信息。然而，在我们的方法中，我们试图构建一个更有效的视频理解模型，并设计了高斯邻域注意力来捕捉视频片段中的时空依赖性。此外，提出了多焦点机制来显式解决尺度变化问题。另外，在[25]中提出了一个大规模的无人机视角视频人群数据集（DroneCrowd）。尽管DroneCrowd中的人群密度高于我们提出的VSCrowd，但我们的数据集在四个方面优于DroneCrowd：1) 我们数据集中的视频是监控视频，其中强烈的透视效应导致人头尺度发生显著变化。然而，DroneCrowd中由无人机摄像头捕获的人体对象在同一视频中尺度是一致的。因此，VSCrowd比DroneCrowd更具挑战性。2) VSCrowd中人体对象在面部朝向、姿态、大小等方面的多样性更大。但DroneCrowd中的对象只是从高处捕获的几个像素。我们数据集的多样性可以有效提高深度模型的鲁棒性。3) VSCrowd在公共安全方面有更多的应用，因为我们的视频是现实生活中各种场景下人群的真实监控。4) 除了人头中心，我们还为每个人标注了一个覆盖头肩区域的边界框，并带有ID标签。因此，除了人群计数和定位外，VSCrowd还可以应用于其他任务，如微小人脸检测、行人重识别和目标跟踪。总之，我们的工作在方法论和数据集收集方面与STANet有显著差异。

B. 注意力机制

注意力机制最初在自然语言处理（NLP）领域被提出，用于对齐输入序列和输出序列[60]。与基于LSTM的编码器-解码器架构配合使用，它在捕捉序列中的长距离依赖性方面展现了强大的能力。此外，研究人员基于多头注意力机制提出了Transformer，其中在不同方面捕捉全局依赖性[61]。最先进的语言模型就是基于Transformer构建的[62]。

受其在NLP领域巨大成功的启发，注意力机制已被引入计算机视觉领域[63], [64], [65], [66], [67], [68], [69]。提出了挤压-激励（SE）块来建模通道间的依赖关系[64]。通过学习通道级注意力，可以在略微增加计算成本的情况下显著提高CNN的性能。开发了非局部块[65]来捕捉像素间的长距离依赖性，它可以作为通用操作插入到经典CNN中。许多计算机视觉任务，如视频分类和目标检测，都得到了改进。受其在处理序列方面巨大成功的激励，Transformer已被用于计算机视觉任务。在[36]中提出了DETR，其中目标检测被建模为编码器-解码器架构中的序列生成过程。考虑到自注意力的计算复杂度与序列长度成二次方关系，提出了许多稀疏注意力机制。例如，在[41]中提出了可变形DETR，其中查询只关注从其邻域采样的少量键。在[66]中提出了独立自注意力，其中查询只关注其周围的键。基于独立自注意力机制，在这项工作中通过替换所有空间卷积提出了一个完全注意力视觉模型。本质上，所提出的高斯邻域注意力也是一种稀疏注意力，但它结合了局部注意力和随机注意力的优点，在不丢失视频数据拓扑结构的情况下捕捉像素间的长距离依赖性，同时消耗更少的计算资源。此外，开发了多焦点GNA来处理监控中强烈透视效应引起的尺度变化。

C. 多焦点技术

多焦点技术最近在其他计算机视觉任务中得到了探索，如分类和分割。例如，在[70]中提出了一种基于空间和放大倍数的注意力采样策略，其中注意力网络预测不同放大倍数下信息块的空间概率分布。尽管该方法试图以多分辨率理解大尺度组织病理学图像，但它与我们的方法不同，我们的方法显式地建模了不同范围的像素级依赖性，以将时空信息聚合到查询像素中。在[71]中引入了中央凹模块，对于下采样图像的每个位置，估计该位置周围不同大小块的重要性。通过为每个位置聚合各种块，提高了兆像素组织学图像的分割性能。该方法通过简单地裁剪不同大小的块并估计其重要性（块级注意力）来提取多焦点语义信息。相比之下，我们的方法利用像素级注意力在不同尺度的高斯邻域内捕捉像素间的长距离依赖性。

III. VSCROWD 数据集

我们创建了一个名为VSCrowd的大规模视频数据集，全面覆盖了各种人群场景，如广场、购物中心、十字路口和校园。VSCrowd中的视频要么从互联网收集，要么由静态摄像头捕获。VSCrowd数据集与另一个大规模视频人群数据集DroneCrowd[25]的主要区别在于，DroneCrowd中的视频由无人机视角摄像头记录，而VSCrowd专注于监控视角。

具体来说，VSCrowd中的视频以25-30帧每秒（FPS）的速度收集，最高分辨率为1920 × 1080。为了减少视频中的时间冗余，收集的视频被下采样至5 FPS。对DroneCrowd也应用了类似的预处理。然后我们将所有视频分割成大约20秒的镜头。也就是说，每个镜头包含大约100帧。最后，共收集了634个镜头（总计62,938帧）。所提出的VSCrowd的标注工作是在SenseTime集团有限公司设计的标注平台SenseBee上进行的。在标注之前，我们为该过程设定了严格的协议，包括人头中心和头肩区域的明确定义、处理模糊/遮挡区域的方法以及几种特殊情况的解决方案（镜子/汽车中的人、自行车上的人、婴儿车中的婴儿等）。在标注过程中，每个标注员被分配了几个视频，并要求他们为每一帧提供以下真实标签：人头中心、覆盖头肩区域的边界框以及每个人的唯一ID。值得一提的是，我们允许标注员通过查看相邻帧来合理估计模糊人员的位置。因此，对于视频中的每个人，我们知道其在任意时刻的确切位置。超过30名训练有素的标注员花费了三个月的时间完成了所有视频的标注。标注完成后，额外的工作人员负责检查标签的正确性和质量。经过检查和修正，我们确保标签的准确率超过97%。最后，获得了2,344,276个人头标签（即每个镜头约3,698个，每帧37个）。图1展示了所提出的VSCrowd中的一些标注帧。

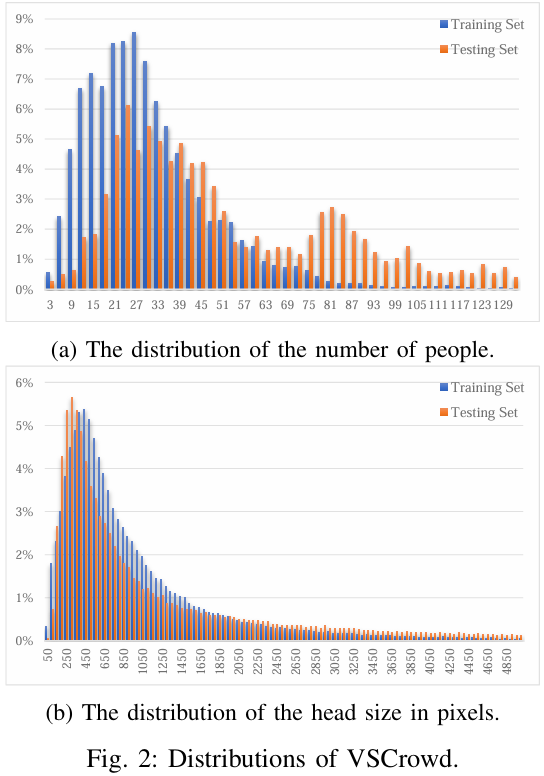
关于训练集和测试集的构建，我们在视频级别上对VSCrowd进行划分，即训练集和测试集包含不同的视频。此外，为了使我们的数据集更具挑战性，我们确保训练集中的场景与测试集中的场景不同。我们之所以以这种方式划分VSCrowd，是因为我们希望模型通过在不同场景的视频上进行训练和测试来学习场景无关的表示。在这种情况下，在我们的数据集上表现更好的模型意味着它具有更好的泛化能力，在处理新场景时更强大。具体来说，VSCrowd被划分为一个训练集（497个镜头/78.4%）和一个测试集（137个镜头/21.6%），这两部分之间存在很大的场景差距。我们提供了更多关于所提出的VSCrowd的统计数据，包括每帧人数分布（图2a）和以像素为单位的人头大小分布（图2b）。如图所示，测试集包含的人数比训练集多。训练集和测试集之间的分布差距使我们的数据集更具挑战性。就人头大小的分布而言，训练集和测试集中都是长尾分布。该分布表明所提出的数据集中人头大小存在很大差异，这是与其他人群数据集相比的一个显著特征。

IV. 所提出的方法

在本节中，我们详细阐述了所提出的多焦点高斯邻域注意力（GNA）模块，并基于多焦点GNA设计了一种用于人群定位的新结构。

A. 多焦点高斯邻域注意力

注意力机制在计算机视觉中得到了很好的利用[72], [73]。给定一个查询集 {qj}\{\boldsymbol{q}_{j}\}{qj​} 和一个键值对集 $\{(k_i,v_i)\}$，其中 ${\mathbf{q}}_j,{\mathbf{k}}_i,{\mathbf{v}}_i\in {\mathbb{R}}^d$，${\mathbf{q}}_j$ 的注意力输出计算如下：
Attn⁡(qj)=∑isoftmax⁡i(s(qj,ki))vi,=∑iexp⁡{s(qj,ki)}∑kexp⁡{s(qj,kk)}⋅vi,\begin{aligned}\operatorname{Attn}(\boldsymbol{q}_{j})&=\sum_{i}\operatorname{softmax}_{i}(s(\boldsymbol{q}_{j},\boldsymbol{k}_{i}))\boldsymbol{v}_{i},\\ &=\sum_{i}\frac{\exp\{s(\boldsymbol{q}_{j},\boldsymbol{k}_{i})\}}{\sum_{k}\exp\{s(\boldsymbol{q}_{j},\boldsymbol{k}_{k})\}}\cdot\boldsymbol{v}_{i},\end{aligned}Attn(qj​)​=i∑​softmaxi​(s(qj​,ki​))vi​,=i∑​∑k​exp{s(qj​,kk​)}exp{s(qj​,ki​)}​⋅vi​,​
其中 $s({\mathbf{q}}_j,{\mathbf{k}}_i)$ 是衡量键 ${\mathbf{k}}_i$ 和查询 ${\mathbf{q}}_j$ 之间相似性的得分函数。本质上，注意力机制是基于查询与相应键的相似性对值进行的加权平均。缩放点积相似性[61]在近期的工作中得到了很好的利用并展现出极大的稳定性[37]。在本文中，我们使用缩放点积作为得分函数，即 $\widetilde{s({\mathbf{q}}_j,{\mathbf{k}}_i)}=\frac{{\mathbf{q}}_j^{\mathrm{T}}{\mathbf{k}}_i}{\sqrt{d}}$。

传统全注意力的一个主要问题是其相对于序列长度的二次方时间和内存复杂度，这限制了其在许多场景中的应用。由于全注意力的复杂度过高，近期文献中提出了许多高效的变体。例如，[66], [74]提出了局部注意力，其中每个查询只能连接到其固定邻域内的键，因此注意力保留了数据中的拓扑结构。然而，局部注意力无法捕捉查询与固定邻域外键之间的依赖关系。在[42]中利用了随机注意力，其中每个查询只关注从整个集合中均匀采样的少量键，因此每个查询以线性计算成本捕捉到某些全局信息。但由于两个相距较远的像素通常不相关，因此会引入冗余信息。

在本文中，我们提出了高斯邻域注意力（GNA），其中每个查询关注从其高斯随机邻域中采样的键。本质上，所提出的高斯邻域注意力是随机邻域注意力（RNA）的一种特殊情况。在这种情况下，我们首先解释一般的RNA，然后基于RNA具体说明GNA如下。以二维特征图为例，假设 $\mathbf{Q},\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{H\times W\times d}$ 分别是查询、键和值，对于 $\mathbf{Q}$ 上的每个位置 $\mathbf{x}$，我们从邻域采样分布的角度将RNA表述为期望：
$$\begin{array}{r}RNA({\mathbf{Q}}_{\mathbf{x}},N,{\mathcal{P}}_N)={\mathbb{E}}_{({\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N)\sim {\mathcal{P}}_N}\left[\mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})\right],\\ \mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})=\sum _{i=1}^N{\mathrm{softmax}}_i\left(\frac{{\mathbf{K}}_{{\mathbf{x}}_i}^{\mathrm{T}}{\mathbf{Q}}_{\mathbf{x}}}{\sqrt{d}}\right){\mathbf{V}}_{{\mathbf{x}}_i},\end{array}$$
其中 $N$ 是预定义的用于注意力的采样点数，${\mathcal{P}}_N$ 是均值为 $\mathbf{x}$ 的 $N$ 个独立同分布的二维分布（如二维高斯分布、拉普拉斯分布和学生t分布）的联合分布。因此，${\mathcal{P}}_N$ 是一个 $2N$ 维分布，均值为 $(x,\cdots ,x)\in {\mathbb{R}}^{2N}$。通过将不同的分布应用于 ${\mathcal{P}}_N$，可以构建不同的RNA机制。例如，通过在整个空间范围内应用均匀分布来构建完全随机注意力。在本文中，我们提出对RNA使用预定义标准差 $\gamma$ 的二维高斯分布，并具体说明高斯邻域注意力。

GNA中预定义的标准差 $\gamma$ 至关重要，因为它控制着信息聚合的区域范围。与固定圆形邻域上的均匀分布相比，查询点周围的高斯采样具有以下优势。在 $\mathrm{GNA}$ 中，大多数采样点落在均值周围 $3\gamma$ 的区域内，并且离查询越近，采样点越密集，这是首选的，因为一般来说，离查询越近的像素与查询的相关性越高。然而，如果我们在一个半径为 $3\gamma$ 的圆形邻域内均匀采样点，更多的采样键可能会出现在远离中心点的位置，从而在注意力计算中引入更多相关性较低、信息量较少的键。

监控的一个显著特征是强烈的透视效应，这会导致物体的尺度变化。如先前工作所述，这是检测任务中的一个主要挑战，可能导致一个物体的多次检测（低mAP）或漏检（低mAR）。为了克服VSCrowd中人头严重的尺度变化，我们的模型中使用了多焦点GNA（MF-GNA）。具体来说，将标准差 $\gamma$ 设置为不同的值，并通过平均计算MF-GNA的输出。这种做法还可以提高模型捕捉长距离依赖的能力，解释如下。形式上，所提出的MF-GNA的定义表示如下：
$$\mathrm{MFGNA}=\frac{1}{F}\sum _{f=1}^F{\mathbb{E}}_{z\sim {\mathcal{N}}_N^{{\gamma }_f}}\left[\mathrm{Attn}(Q_x)\right],$$
其中 $z:=(x_1,\cdots ,x_N)$，$F$ 是预定义的焦点数，${\mathcal{N}}_N^{{\gamma }_f}$ 是一个 $2N$ 维高斯分布，均值为 $(x,\cdots ,x)\overleftrightarrow{\in }{\mathbb{R}}^{2N}$，每个维度的标准差为 ${\gamma }_f$。可以推导出
$$\begin{array}{rl}\mathrm{MFGNA}& =\frac{1}{F}\sum _{f=1}^F{\mathbb{E}}_{z\sim {\mathcal{N}}_N^{{\gamma }_f}}\left[\mathrm{Attn}(Q_x)\right]\\ & =\frac{1}{F}\sum _{f=1}^F\int p_{{\mathcal{N}}_N^{{\gamma }_f}}(z)\mathrm{Attn}(Q_x)\mathrm{d}z\\ & =\int \left[\sum _{f=1}^F\frac{1}{F}{p}_{{\mathcal{N}}_N^{{\gamma }_f}}(z)\right]\mathrm{Attn}(Q_x)\mathrm{d}z.\end{array}$$
令 $M$ 表示 $\{{\mathcal{N}}_N^{{\gamma }_f}{\}}_{f=1}^F$ 的均匀混合。
$$p_{\mathcal{M}}(z)=\sum _{f=1}^F\frac{1}{F}{p}_{{\mathcal{N}}_N^{{\gamma }_f}}(z).$$
那么，
$$\begin{array}{rl}\mathrm{MFGNA}& =\int \left[\sum _{f=1}^F\frac{1}{F}{p}_{{\mathcal{N}}_N^{{\gamma }_f}}(z)\right]\mathrm{Attn}(Q_x)\mathrm{d}z\\ & =\int p_{\mathcal{M}}(z)\mathrm{Attn}(Q_x)\mathrm{d}z\\ & ={\mathbb{E}}_{z\sim \mathcal{M}}\left[\mathrm{Attn}(Q_x)\right]=\mathrm{RNA}(Q_x,N,\mathcal{M}).\end{array}$$
因此，所提出的多焦点GNA等价于具有均匀混合高斯分布的随机邻域注意力。此外，根据[75]，我们可以假设存在一个长尾分布 $\mathcal{H}$ 使得
$$p_{\mathcal{H}}(z)\approx p_{\mathcal{M}}(z).$$
那么所提出的多焦点GNA可以进一步近似如下：
$$\begin{array}{rl}\mathrm{MFGNA}& =\int p_{\mathcal{M}}(\mathbf{z})\mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})\mathrm{d}\mathbf{z}\approx \int p_{\mathcal{H}}(\mathbf{z})\mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})\mathrm{d}\mathbf{z}\\ & ={\mathbb{E}}_{\mathbf{z}\sim \mathcal{H}}\left[\mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})\right]=\mathrm{RNA}({\mathbf{Q}}_{\mathbf{x}},N,\mathcal{H}).\end{array}$$
总之，所提出的多焦点GNA也可以看作是具有长尾分布的随机邻域注意力。因此，多焦点机制可以提高模型捕捉像素间长距离依赖的能力。配备了多焦点机制的GNA在mAP和mAR之间取得了良好的平衡。为简单起见，在本文的其余部分，除非另有说明，GNA指的是多焦点GNA。

凭借局部注意力和随机注意力的双重优势，所提出的GNA不仅保持了原始数据的拓扑结构，而且以线性计算成本捕捉长距离依赖。关于所提出的GNA与其他稀疏注意力机制的理论分析见附录A。请注意，采样操作是计算图中的一个叶节点，因此GNA相对于输入特征图（Q, K, V）是可微的。由于GNA中的高斯采样，模型的训练和测试中存在随机性。训练中的随机性就像典型神经网络中的dropout，可以提高GNANet的鲁棒性。然而，测试中的随机性是不希望的。为了提高模型在测试中的稳定性，我们使用蒙特卡洛积分来近似期望：
$$\begin{array}{rl}GN{A}_{test}& ={\mathbb{E}}_{({\mathbf{x}}_1,\cdots ,{\mathbf{x}}_N)\sim {\mathcal{N}}_N^{\gamma }}\left[\mathrm{Attn}({\mathbf{Q}}_{\mathbf{x}})\right]\\ & \approx \frac{1}{T}\sum _{t=1}^T\sum _{i=1}^N{\mathrm{softmax}}_i\left(\frac{{\mathbf{K}}_{{\mathbf{x}}_i^t}^T{\mathbf{Q}}_{\mathbf{x}}}{\sqrt{d}}\right){\mathbf{V}}_{{\mathbf{x}}_i^t},\end{array}$$
其中 {(x1t,⋯ ,xNt)}t=1T\left\{(\pmb{x}_{1}^{t},\cdots,\pmb{x}_{N}^{t})\right\}_{t=1}^{T}{(x1t​,⋯,xNt​)}t=1T​ 是 $(x_1,\cdots ,x_N)$ 的 $T$ 组采样结果。在实践中，我们在测试阶段多次计算GNA，并取平均值作为GNA模块的最终输出。

B. 通过GNA进行视频人群定位

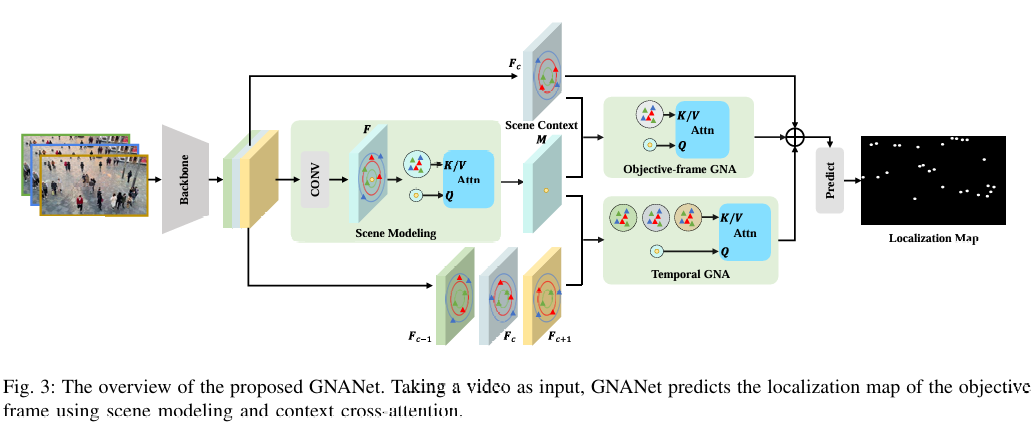
在本小节中，我们提出了一种基于多焦点高斯邻域注意力的新网络结构，称为GNANet，用于视频人群定位。请注意，为了减少相邻帧之间的时间冗余，我们在进行人群定位之前首先将视频下采样到较低的帧率。GNANet的概述如图3所示。它以一个帧序列（下采样后）作为输入，并预测目标帧（定义为中心帧）的定位图。GNANet由四个模块组成：骨干网络、场景建模模块、上下文交叉注意力模块和定位预测模块。下面分别详细阐述。

1. 骨干网络。骨干网络将片段中的每一帧作为输入，并独立地从每一帧中提取语义特征。考虑到VGGNet[76]在人群分析中表现出强大的能力[24], [45], [10]，我们采用预训练的VGGNet作为骨干网络。具体来说，我们使用VGG16的前13层从帧中提取信息特征。给定一个包含 $m$ 帧的视频片段 $V^i={\left\{f_j^i\right\}}_{j=0}^{m-1}$，其中 ${\mathbf{f}}_j^i\in \widetilde{{\mathbb{R}}^{H\times W\times 3}}$，$i$ 是片段索引，骨干网络从每一帧中提取特征。片段 $V^i$ 的特征图记为 ${\left\{F_j^i\right\}}_{j=0}^{m-1}$，其中 $F_j^i\in {\mathbb{R}}^{\frac{H}{8}\times \frac{W}{8}\times 512}$。请注意，中间帧 $f_c^i(c:=\lfloor \frac{m}{2}\rfloor )$ 被定义为该片段的目标帧。为简单起见，在本小节的其余部分省略片段索引 $i$。

2. 场景建模。场景建模对于人群分析非常重要，尤其是在摄像头静止的监控场景中。在这项工作中，我们使用所提出的 $\mathrm{GNA}$ 来计算场景上下文。具体来说，通过卷积（输入通道512m，输出通道512，卷积核大小(3,3)）和ReLU将片段中所有帧的特征 $F_j\in {\mathbb{R}}^{\frac{H}{8}\times \frac{W}{8}\times 512}$ 聚合起来。片段的聚合特征记为 $F\in {\mathbb{R}}^{\frac{H}{8}\times \frac{W}{8}\times 51\tilde{2}}$。为了捕捉视频片段中的长距离依赖，对 $F$ 进行高斯邻域自注意力（GNA）计算。具体来说，公式(2)和(3)中GNA的 $\mathbf{Q},\mathbf{K},\mathbf{V}$ 都定义为 $F$。将注意力输出与聚合特征 $F$ 沿通道维度拼接，并送入一个卷积层，以获得最终的场景上下文 $M\in {\mathbb{R}}^{\frac{H}{8}\times \frac{W}{8}\times 512}$。由于我们应用所提出的GNA来聚合所有帧的信息，因此获得的场景上下文 $M$ 包含了帧序列中重要的像素级语义依赖。

3. 上下文交叉注意力。在获得片段的场景上下文 $M$ 后，网络分别从整个片段和目标帧中检索信息。为了从整个片段中检索信息，我们为 $M$ 上的每个空间位置从片段中的每一帧采样固定数量的点。所有帧的采样点的并集被作为键值索引集。然后，通过将 $M$ 作为查询，将从所有帧采样的特征作为键/值，计算时间GNA。为了从目标帧中检索信息，我们直接计算目标帧GNA，即将 $M$ 作为查询，将从目标帧采样的特征作为键/值，即 $\mathbf{K}=\mathbf{V}={\mathbf{F}}_c,\mathbf{Q}=\mathbf{M}$。最后，将这两个注意力输出与目标帧特征 ${\mathbf{F}}_c$ 的逐元素和送入预测模块。请注意，尽管我们的目标是预测目标帧的定位结果，但我们并不期望一个完美的目标帧特征，而是利用包含目标帧的短视频片段的时空特征。所获得的时空特征应该能够意识到哪个是目标帧，而不是只关注它。

4. 定位预测。定位预测模块的输入是一个包含片段时空信息的512维特征图。请注意，特征图的空间大小是原始帧的 $1/8$，因此定位预测模块需要将特征图上采样到与原始帧空间大小相同的单通道定位图。在这项工作中，我们遵循RAZNet[24]中定位分支的设计来获得定位图。具体来说，首先应用三个卷积层（输出通道512，卷积核大小(3,3)，膨胀率(2,2)）来进一步提取语义特征。然后，通过三个反卷积层（卷积核大小(3,3)，步长(2,2)，输出通道256/128/64）进一步处理特征图，每个反卷积层后面都跟着一个卷积层（卷积核大小(3,3)，膨胀率(2,2)），不改变通道数。请注意，所有卷积/反卷积层后面都跟着ReLU激活函数。由于每个反卷积层将特征图的空间大小加倍，因此输出是一个与原始图像大小相同的64维特征图。最后，一个 $1\times 1$ 卷积（带sigmoid激活）将特征图转换为单通道定位图，指示一个像素是人头中心的概率。

C. 实现细节

GNANet的训练遵循监督学习的标准程序。我们将训练集记为 ${\left\{\left(V^i,L^i\right)\right\}}_{i=1}^M$，其中 Li∈{0,1}H×W\pmb{L}^{i}\in\{0,1\}^{H\times W}Li∈{0,1}H×W 是片段 $V^i$ 的目标帧的真实二值图，通过处理人头标注获得，方法与[24]中相同。给定GNANet（记为 $G_{\theta }$，参数为 $\theta$），目标是解决以下问题：
$${\mathbf{\theta }}^{\ast }=\underset{\mathbf{\theta }}{\mathrm{argmin}}\frac{1}{M}\sum _{i=1}^M\mathcal{L}\left(G_{\mathbf{\theta }}(V^i),{\mathbf{L}}^i\right),$$
其中 $\mathcal{L}$ 是损失函数。具体来说，我们使用加权二元交叉熵损失，其中正样本权重设置为50，以补偿定位图中正负样本之间的严重不平衡。

对于后处理，我们遵循[24], [25]中的实现，计算定位图的局部峰值并预测人头的确切位置。考虑到性能和GPU内存限制，我们将视频片段的长度 $m$ 设置为3。对于所提出的多焦点GNA，高斯分布的标准差 $\gamma$ 确定为3、5和10。在大多数人头数据集中，微小人头的大小在特征图上可能只有几个像素（在极端情况下甚至只有一个像素）。对于相对较大的人头，它们在特征图上的大小不会超过30个像素。就我们选择的最小标准差 $(\gamma =3)$ 而言，采样的键几乎都在以查询像素为中心、半径为9的圆内，而对于最大的标准差 $(\gamma =10)$，半径为30。高斯邻域足以覆盖一个人头的区域。此外，为每个焦点采样32个点作为键值索引。在第V-E节中对GNA中的超参数进行了更多分析。在训练方面，我们的模型使用小批量随机梯度下降法训练30个周期，学习率固定为 $2\times 10^{-6}$。批量大小设置为16。所有实验均在NVIDIA V100 (32 GB)上使用PyTorch进行。

V. 实验

在本节中，我们首先解释定位和计数的评估指标。然后，我们将所提出的GNANet与VSCrowd、FDST[27]、Venice[7]、DroneCrowd[25]、ShanghaiTech[53]、UCF-QNRF[55]和NWPU[4]上的先前定位方法和计数方法进行比较。最后，我们对GNANet进行消融研究和进一步分析，以验证所提出模块的有效性。

A. 评估指标

在这项工作中，我们使用MS-COCO[77]中关键点检测的评估协议来评估定位方法，如[24]中所述。具体来说，标准平均精度（AP）和平均召回率（AR）被作为定量指标。
mAP通过从AP.50到AP.95（步长为0.05）的结果平均计算得出。
对于计数性能的评估，应用了平均绝对误差（MAE）和均方根误差（RMSE），其计算公式如下：
$$\begin{array}{rl}& MAE=\frac{1}{M}\sum _{i=1}^M|{\hat{C}}_i-C_i|,\\ & RMSE=\sqrt{\frac{1}{M}\sum _{i=1}^M({\hat{C}}_i-C_i{)}^2},\end{array}$$
其中 ${\hat{C}}_i,C_i$ 分别是第 $i$ 张图像的估计人头数和真实人头数，$M$ 是图像数量。

B. 与最先进方法的比较

在本节中，我们将我们的方法与VSCrowd、FDST[27]、Venice[7]、ShanghaiTech[53]和UCF-QNRF[55]上的现有人群定位方法进行比较。

1) VSCrowd数据集上的定位

在本小节中，我们在所提出的VSCrowd数据集上将GNANet与先前典型的人群定位方法（RAZNet[24]主网络中的定位分支、STANet[25]的定位分支和P2PNet[58]）以及经典的目标检测方法（Faster-RCNN[15]和FCOS[13]）进行比较。RAZNet是一个单图像人群定位网络，用于预测给定图像中人头的位置。STANet是唯一一个通过视频片段估计定位结果的视频人群定位方法。然而，它是专门为无人机视角的人群视频设计的。P2PNet是一个纯粹的基于点的框架，用于人群定位，它直接预测代表人头中心的点提案。对于Faster-RCNN和FCOS，它们使用VSCrowd中提供的头肩框标注进行训练，并在测试时将框中心视为人头中心。我们还评估了最先进的群体计数方法Generalized Loss[57]的定位性能。通过在预测的密度图上寻找局部峰值来获得定位结果。结果如表II所示。

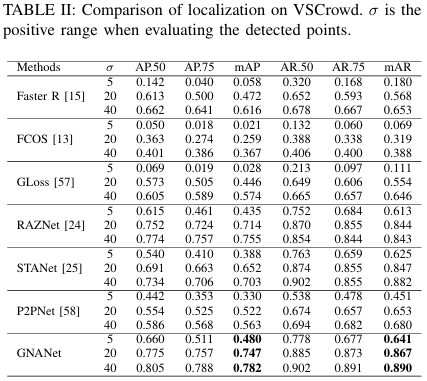
如表II所示，当 $\sigma$ 较小时，目标检测方法在人头中心定位方面的表现很差，这意味着基于检测的方法无法准确定位人头中心。当 $\sigma$ 变大时，两阶段检测器Faster R-CNN达到了相当的精度，但召回率仍然很差。结果表明，目标检测方法可以检测到相对较大的人头，而无法准确定位拥挤场景中的微小人头。总之，传统的基于检测的方法无法处理人群定位任务。至于使用广义损失训练的计数模型，它表现出较差的定位性能，尤其是在小 $\sigma$ 下。结果表明，计数方法在定位拥挤或远处区域的小人头方面能力较弱。

此外，单图像定位方法RAZNet取得了相当不错的性能，为所提出的数据集设定了一个强有力的基线。然而，STANet在VSCrowd上的AP和AR表现都很差。我们认为导致这些结果的主要原因是STANet是专门为无人机视角的人群场景设计的，其特征与监控场景大不相同。此外，最先进的方法P2PNet在我们的数据集上取得了更低的结果。我们假设原因是训练集和测试集之间存在很大的分布差距，而P2PNet无法处理这个问题，因为训练中使用的超参数与数据集的属性高度相关。至于所提出的方法，GNANet在各种 $\sigma$ 值下均在AP和AR方面取得了最佳结果，这意味着我们的方法不仅能找到人头的位置，还能精确定位人头中心。

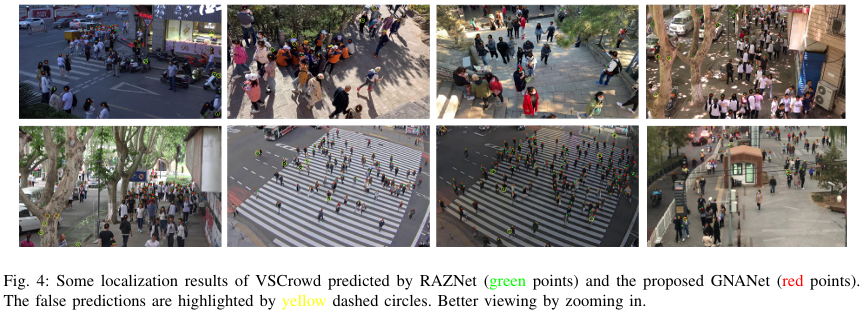
图4展示了RAZNet和GNANet在VSCrowd上的一些预测结果。如图所示，我们的方法可以准确定位人头中心，并很好地处理人头大小的变化。除了RAZNet，我们还在VSCrowd上与最先进的方法P2PNet进行了可视化比较。定位预测结果如图5所示，其中红点/绿点分别是GNANet/P2PNet的预测结果。第一行的两张图像展示了在远处区域定位小人头的性能。我们可以看到，P2PNet漏掉了大部分人员，而我们的方法以高精度检测到了大多数人头。第二行展示了在拥挤的夜间场景中的预测结果。在这种情况下，P2PNet几乎无法检测到人头，而我们的方法仍然表现良好。最后一行展示了对遮挡和模糊的鲁棒性。我们可以看到，对于一些被遮挡或模糊的人员，我们的方法仍然可以定位他们。总之，比较结果表明我们的模型在处理小人头和具有挑战性的场景方面优于P2PNet。

2) FDST数据集上的定位

在本小节中，我们在FDST数据集上将所提出的GNANet与RAZNet、STANet、广义损失和P2PNet进行比较。FDST是一个用于人群分析的监控数据集，包含15,000帧和394,000个标注人头，来自13个不同场景。它与VSCrowd类似，但样本较少。结果如表III所示。

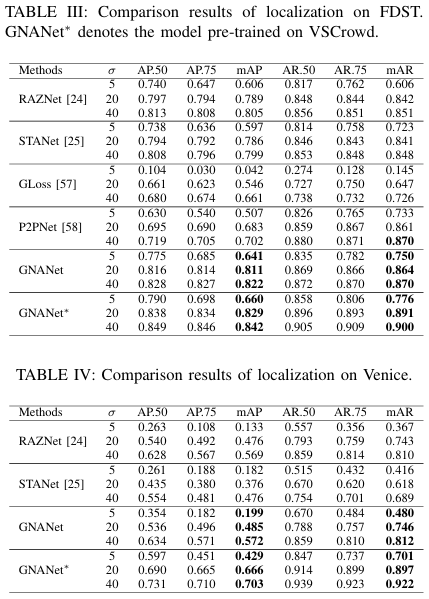
如表III所示，GNANet在各种 $\sigma$ 下都优于其他方法（包括定位方法RAZNet、STANet和P2PNet，以及最先进的计数方法广义损失）。请注意，所有方法在FDST上的性能都远高于在所提出的VSCrowd上的性能，这表明VSCrowd比FDST更具挑战性。VSCrowd拥有更多的场景和更多的人，足以全面评估人群分析方法的性能。

此外，为了揭示大规模监控数据集的重要性，我们首先在VSCrowd上预训练GNANet，然后在FDST上进行微调。微调后的模型记为GNANet*。如表III所示，微调模型GNANet*在不同 $\sigma$ 值下的AP和AR方面都比GNANet有大幅提升。性能的提升是意料之中的，因为大量的训练样本赋予了模型强大的泛化能力。

3) Venice数据集上的定位

我们还在Venice这个用于人群分析的视频数据集上评估了我们的方法。结果如表IV所示。从结果可以看出，我们的方法显著优于RAZNet和STANet。值得注意的是，Venice是一个由有限帧组成的小数据集。结果表明，当训练样本稀缺时，我们的方法不易过拟合。

此外，我们在VSCrowd上预训练我们的模型，然后在Venice上进行微调。微调后的模型在精度和召回率方面都显示出巨大改进，这证明了VSCrowd大规模数据集的重要性。

4) DroneCrowd数据集上的定位

我们还在DroneCrowd上评估了我们的方法，这是一个无人机视角的人群视频数据集。与FDST、Venice和我们的VSCrowd不同，DroneCrowd是从鸟瞰视角收集的，只能看到人头的顶部。由于没有透视效应，数据集中的人头只有几个像素。因此，我们只在表V中报告了 $\sigma =5$ 和 $\sigma =20$ 下的性能。比较的方法包括RAZNet（一个强大的基线方法）、STANet（专门为DroneCrowd设计）和P2PNet（最先进的定位方法）。在比较的方法中，P2PNet和STANet分别在 $\sigma =5$ 和 $\sigma =20$ 下实现了最佳的mAP性能。此外，STANet和我们的方法分别在 $\sigma =5$ 和 $\sigma =20$ 下实现了最佳的mAR性能。尽管我们的模型不是专门为无人机视角的人群场景设计的，但它在这个数据集上仍然表现出相当不错的性能。

5) ShanghaiTech数据集上的定位

除了通过视频进行人群定位外，GNANet还可以适应单图像人群定位模型。具体来说，丢弃GNANet中的场景建模模块和时间GNA，直接使用图像特征作为场景上下文，并在其上计算自GNA。将注意力输出与原始特征结合后送入预测模块。其他过程和设置与视频定位相同。GNANet的单图像输入版本记为S-GNANet。我们在ShanghaiTech数据集（A部分和B部分）[53]上将S-GNANet与典型的单图像人群定位方法RAZNet[24]进行比较。结果如表VI（A部分）和表VII（B部分）所示。

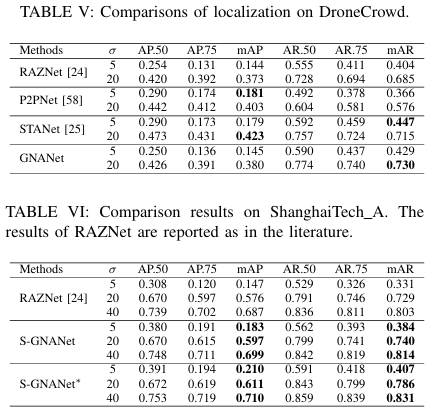
如表VI和表VII所示，S-GNANet在不同 $\sigma$ 值下均优于RAZNet。我们还注意到，随着 $\sigma$ 的减小，S-GNANet的改进变得更加显著。由于 $\sigma$ 控制着检测被视为真正例的正范围，小的 $\sigma$ 意味着检测到的人头被视为真正例的阈值更严格，而大的 $\sigma$ 使得改进不那么明显。因此，结果表明S-GNANet比RAZNet能更精确地预测人头中心。

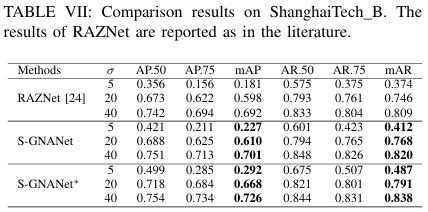
此外，为了揭示大规模监控数据集的重要性，我们首先在所提出的VSCrowd上预训练S-GNANet，然后分别在ShanghaiTech_A和ShanghaiTech_B上进行微调。微调后的模型记为S-GNANet*。如表VI和表VII所示，S-GNANet*的召回率远高于S-GNANet。与ShanghaiTech_A相比，ShanghaiTech_B的分布与所提出的VSCrowd更为相似，因此在ShanghaiTech_B上的改进比在ShanghaiTech_A上更显著。我们得出结论，通过在VSCrowd上进行预训练，可以极大地促进在困难场景中对人群的识别。

6) UCF-QNRF数据集上的定位

我们还在UCF-QNRF上评估了我们的方法，这是一个比ShanghaiTech A和B更大的数据集。结果如表VIII所示。请注意，广义损失的结果是使用作者提供的预训练模型获得的。具体来说，广义损失在所有 $\sigma$ 下的表现都不如定位方法有竞争力，这表明计数方法在预测确切的人群位置方面存在不足。

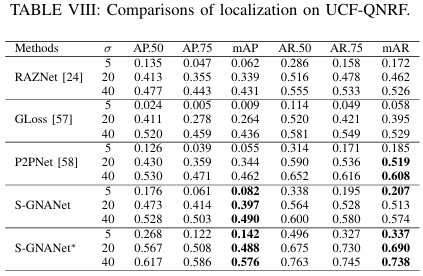
此外，RAZNet和S-GNANet在检测小人头方面的性能相当。然而，对于更大的 $\sigma$，S-GNANet在精度和召回率方面都表现出更好的结果，这意味着我们的方法在处理大人头方面更强大。至于与P2PNet的比较，我们的模型在所有 $\sigma$ 下的精度都优于它，而P2PNet在更大的 $\sigma$ 下召回率更高。我们发现P2PNet倾向于对一个人头进行多次预测，这可以增加拥挤区域的召回率，但在人员较少的场景中会导致更多的误报。此外，我们在VSCrowd上预训练我们的模型，然后在UCF-QNRF上进行微调。定位性能得到了极大提升。

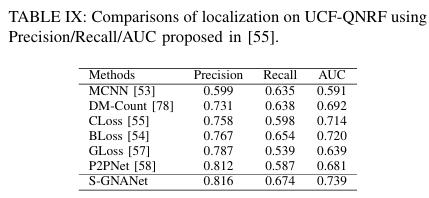
此外，我们使用[55]中提出的度量标准来评估我们的方法。结果如表IX所示。请注意，广义损失的结果是使用作者提供的预训练模型获得的，P2PNet的结果是使用官方代码复现的。从结果可以看出，广义损失和P2PNet的平均精度具有竞争力，但与我们的方法相比，它们的平均召回率较差。由于UCF-QNRF包含大量小人头，广义损失和P2PNet的性能表明它们在检测小人头方面存在不足。

7) NWPU数据集上的定位

我们在NWPU[79]上评估了我们的方法，这是一个在近期工作中广泛使用的人群分析基准。由于测试集的标签未发布，我们报告验证集的结果。所提出的方法与强大的基线方法RAZNet、最先进的计数方法广义损失和定位方法P2PNet进行了比较。结果如表XI所示。结果表明，我们的模型在精度方面显著优于其他方法。同时，该数据集上的召回率结果与UCF-QNRF上的结果相似。

C. 应用于人群计数

我们方法的人群定位结果可以直接用于人群计数。在这种情况下，也评估了我们方法的计数性能。我们将我们的方法（GNANet和S-GNANet）与单图像人群计数方法（MCNN[53]、CSRNet[45]、RAZNet[24]和贝叶斯损失[54]）以及视频人群计数方法（ConvLSTM[26]、LST[27]、STANet[25]和EPF[28]）在VSCrowd和两个公共数据集（FDST和ShanghaiTech）上进行了比较。计数性能的比较结果如表X和表XII所示。

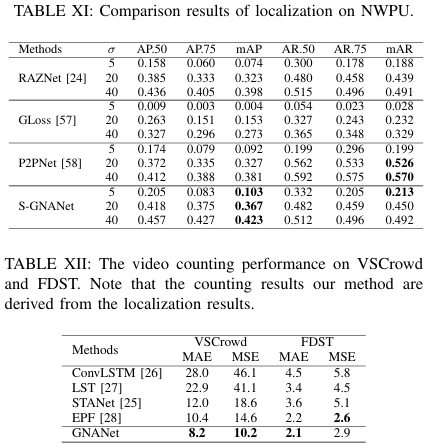
如表X所示，对于单图像计数，S-GNANet优于MCNN和RAZNet的定位分支。至于CSRNet和贝叶斯损失，它们在Shanghai数据集上的性能优于S-GNANet，但它们无法预测人群中人头的确切位置。在VSCrowd数据集上，S-GNANet优于CSRNet，性能略逊于贝叶斯损失。如表XII所示，对于视频人群计数，GNANet在VSCrowd和FDST上优于其他视频人群计数方法。通过考虑时间信息，GNANet超越了贝叶斯损失，并在所有比较方法中取得了最佳结果。

D. 消融研究

在本小节中，我们在GNANet上进行了消融研究。GNANet中有四个关键组件：场景建模模块（SM）、目标帧GNA（F-GNA）、时间GNA（T-GNA）和多焦点机制（MF）。为了验证每个组件的有效性，我们构建了如表XIII所示的GNANet简化版。请注意，没有任何组件的模型是基线模型，其中所有帧的特征通过卷积组合后直接送入预测模块。对于只有SM的模型，计算出的场景上下文被送入预测模块。对于没有MF的模型，$\gamma$ 设置为5。如表所示，基线模型取得了相当不错的性能，尤其是在AR方面。通过添加场景建模，精度和召回率都逐步提高。至于F-GNA和T-GNA，它们都对性能有很大贡献。因此，上下文交叉注意力模块对GNANet至关重要。通过比较最后两行，我们得出结论：多焦点机制在不损害召回率的情况下进一步提高了精度。

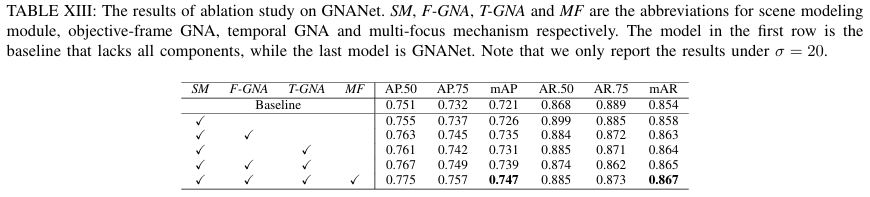
为了证明所提出的高斯邻域注意力（GNA）的有效性，我们构建了GNANet的四个变体：RANet（将GNANet中的GNA替换为随机注意力[42]）、LANet（将GNA替换为局部注意力[66]（查询像素的邻域定义为以查询为中心的9×9大小的块））、DRANet（将GNA替换为圆盘随机注意力（键从以查询为中心、半径为$3\gamma$的圆盘中均匀采样））和DFANet（将GNA替换为最近的可变形注意力[41]）。为了公平比较，GNANet中的多焦点机制被舍弃。注意力机制消融研究的结果如表XIV所示。如表所示，RANet在AP和AR方面都表现不佳，甚至比表XIII中的基线模型还要差。这些结果是可以预见的，因为在计算注意力输出时聚合了不相关和冗余的全局信息。至于配备局部注意力的模型（LANet），与表XIII中的基线模型相比，它表现相当，这意味着局部依赖对视频人群定位至关重要。此外，尽管圆盘随机注意力与所提出的GNA类似，但它只取得了与局部注意力相当的性能。通过学习查询周围键的采样偏移，DFANet在$\sigma$较大时AR方面远优于LANet，这表明邻域变形的重要性。GNA不是使局部邻域可变形，而是将固定邻域扩展到随机邻域，其中像素成为查询邻居的概率由它们的几何距离决定。GNA既能捕捉长距离依赖，又能捕捉局部相关性，基于GNA的GNANet在AP和AR方面都取得了最佳结果。

E. 进一步分析

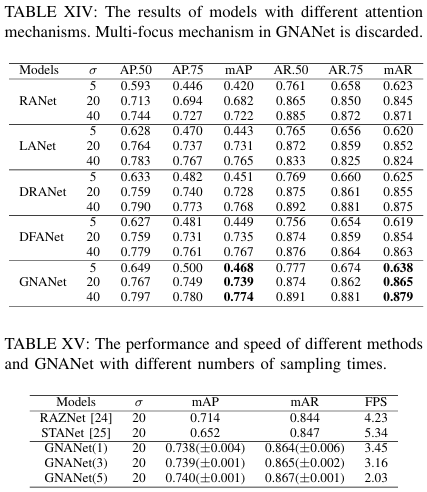
1. GNA的随机性。为了展示GNA在测试时由高斯采样引起的随机性的影响，我们对多采样机制进行了实验，其中GNA被计算多次，并取平均值作为GNA模块的最终输出。我们在表XV中报告了基于5次测试的均值和标准差。请注意，在此实验及后续实验中舍弃了多焦点机制，以使影响更明显。如表XV所示，具有不同采样次数的GNANet在平均mAP和mAR方面表现相似。然而，随着采样次数的增加，性能偏差减小。就时间消耗而言，推理速度随着采样次数的增加而下降，这是意料之中的。为了在性能稳定性和效率之间取得平衡，我们选择在GNA中采样3次，并在所有实验中报告平均性能。此外，我们将我们方法的计算成本与RAZNet和STANet进行了比较。结果表明，尽管GNANet在计算成本方面不如RAZNet和STANet，但它在精度和召回率方面都显著优于其他方法，尤其是与STANet相比。总之，我们的方法在定位精度和计算成本之间取得了合理的平衡。
   

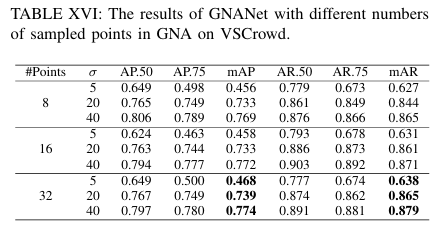
2. 采样点数量的影响。采样点的数量对定位至关重要，因为它控制着聚合到查询的信息量。表XVI展示了具有不同采样点数量的GNANet的性能。如表所示，随着采样数量的增加，GNANet的性能显著提高。我们认为性能提升有两个原因：a) 采样更多的点意味着在为特定查询计算注意力输出时考虑了更多信息；b) GNANet的稳定性得到提高，因为更多的采样点缓解了GNA中的随机性。然而，考虑到计算复杂度，从高斯邻域中采样32个点，旨在在性能和效率之间取得平衡。
   

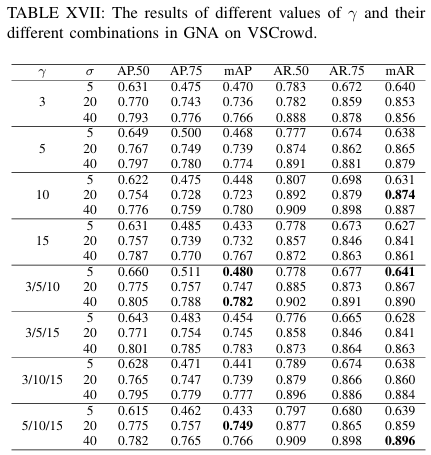
3. GNA中标准差的影响。GNA中高斯分布的标准差 $\gamma$ 在建模人群视频中的人头方面起着重要作用，它控制着信息聚合的范围。为了展示 $\gamma$ 的影响，我们对其进行了实验，结果如表XVII所示。如表所示，具有大/小 $\gamma$ 的GNANet在大/小 $\sigma$ 下表现良好，这意味着不同值的 $\gamma$ 关注不同大小的人头。然而，当 $\gamma =15$ 时，各种 $\sigma$ 下的性能都大幅下降。我们认为 $\gamma =15$ 对于VSCrowd中的人头建模来说太大了，因此在计算注意力输出时向人头中心聚合了冗余信息。此外，我们还在表XVI中比较了GNA中 $\gamma$ 的不同组合。从结果可以看出，多焦点机制在精度和召回率方面都提高了视频人群定位的性能。具体来说，3/5/10的组合在各种 $\sigma$ 下在mAP和mAR之间取得了良好的平衡。在这种情况下，我们选择在多焦点GNA中使用3/5/10的组合。

VI. 结论

在本文中，我们探索了关键的视频人群定位任务，其目标是在视频的目标帧中定位人头。由于用于视频人群分析的大规模监控数据集有限，我们创建了一个名为VSCrowd的基准，这是一个全面且大规模的数据集。为了利用视频中的时空依赖性，我们设计了一种高斯邻域注意力（GNA），它能够捕捉长距离对应关系，同时保持数据中的空间拓扑结构。配备了多焦点机制，GNA可以建模人群场景中人头的尺度变化。基于多焦点GNA，我们开发了一个端到端的网络结构，称为GNANet，以准确地在视频中定位人头，其中利用场景建模模块和上下文交叉注意力模块来聚合时空信息。在VSCrowd和两个公共数据集上的大量实验证明了GNANet的优越性以及所提出模块在视频人群定位和计数方面的有效性。

附录A 稀疏注意力的理论分析

假设 $\mathbf{K},\mathbf{V}\in {\mathbb{R}}^{n\times d}$ 分别是特定查询 $q\in {\mathbb{R}}^d$ 的键矩阵和值矩阵，查询 $\mathbf{q}$ 的全注意力（FA）输出计算为
$$\mathrm{FA}(\mathbf{q},\mathbf{K},\mathbf{V})=\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right)\mathbf{V}\in {\mathbb{R}}^d,$$
其中 $\mathrm{SM}(\cdot )$ 是softmax操作，并使用点积作为得分函数。对于稀疏注意力，我们只选择少量键，其索引集给定为 $\mathcal{P}$。然后，稀疏注意力的键矩阵 $K_1\in {\mathbb{R}}^{n\times d}$ 和值矩阵 ${\mathbf{V}}_1\in {\mathbb{R}}^{n\times d}$ 构造如下，
$$(K_1{)}_{ij}=\{\begin{array}{cc}{K}_{ij},& \mathrm{if}i\in \mathcal{P},\\ 0,& \mathrm{otherwise},\end{array}$$
$$({\mathbf{V}}_1{)}_{ij}=\{\begin{array}{cc}{\mathbf{V}}_{ij},& \mathrm{if}i\in \mathcal{P},\\ 0,& \mathrm{otherwise}.\end{array}$$
类似地，查询 $\mathbf{q}$ 的稀疏注意力（SA）输出计算为
$$\mathrm{SA}(\mathbf{q},{\mathbf{K}}_1,{\mathbf{V}}_1)=\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\right){\mathbf{V}}_1\in {\mathbb{R}}^d,$$
为清晰起见，我们定义以下辅助概念，
$$\begin{array}{rl}& C=\Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right)\Vert ,\\ & {\mathbf{K}}_2=\mathbf{K}-{\mathbf{K}}_1,\\ & {\mathbf{V}}_2=\mathbf{V}-{\mathbf{V}}_1,\end{array}$$
其中 $C$ 是与稀疏注意力无关的常数，${\mathbf{K}}_2,{\mathbf{V}}_2$ 分别由未选择的键和值构造。然后，用稀疏注意力估计全注意力的误差推导如下，
$$\begin{array}{rl}& \Vert \mathrm{FA}(\mathbf{q},\mathbf{K},\mathbf{V})-\mathrm{SA}(\mathbf{q},{\mathbf{K}}_1,{\mathbf{V}}_1)\Vert \\ =& \Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right)\mathbf{V}-\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\right){\mathbf{V}}_1\Vert \\ =& \Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right)\left({\mathbf{V}}_1+{\mathbf{V}}_2\right)-\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\right){\mathbf{V}}_1\Vert \\ =& \Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right){\mathbf{V}}_1+\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right){\mathbf{V}}_2-\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\right){\mathbf{V}}_1\Vert \\ \le & \Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right){\mathbf{V}}_1-\mathrm{SM}\left(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\right){\mathbf{V}}_1\Vert +\Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right){\mathbf{V}}_2\Vert \\ \le & \Vert \mathrm{SM}\left(\mathbf{q}{\mathbf{K}}^{\mathrm{T}}\right)-\mathrm{SM}(\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}})\Vert \Vert {\mathbf{V}}_1\Vert +\Vert \mathrm{SM}(\mathbf{q}{\mathbf{K}}^{\mathrm{T}})\Vert \Vert {\mathbf{V}}_2\Vert \\ \le & \Vert \mathbf{q}{\mathbf{K}}^{\mathrm{T}}-\mathbf{q}{\mathbf{K}}_1^{\mathrm{T}}\Vert \Vert {\mathbf{V}}_1\Vert +C\Vert {\mathbf{V}}_2\Vert \\ =& \Vert \mathbf{q}{\mathbf{K}}_2^{\mathrm{T}}\Vert \Vert {\mathbf{V}}_1\Vert +C\Vert {\mathbf{V}}_2\Vert .\end{array}$$
从误差的上界可以看出，它部分取决于查询 $\mathbf{q}$ 与未参与注意力计算的那些键之间的点积（相似性）。统计上，两个不同位置的特征之间的相似性与其几何距离呈负相关。在这种情况下，与随机注意力相比，所提出的GNA可以以更小的误差期望来估计全注意力，因为在GNA中查询只关注从其邻域采样的键。