面向社科研究者：用深度学习做因果推断（三）

本部分先介绍深度因果估计的三种核心方法：通过 S/T 学习器实现深度结果建模（分别或用单个神经网络建模潜在结果）、借 TARNet（附 TensorFlow/PyTorch 代码）通过共享表示层学习平衡数据、以 Dragonnet 结合 IPW 与半参数理论（靶向正则化）实现双重稳健性；再讲解置信度评估（基于 EIC 计算 Dragonnet 渐近标准误）、模型解释（推荐 SHAP 和集成梯度）及含 5 个实操教程的内容；随后探讨非传统数据的因果推断，包括用 Transformer 处理文本、GNN 处理网络、适配模型处理图像及时变数据；最后总结神经网络在建模非线性异质性等方面的优势、优化难等局限，强调其在因果估计中的未来潜力，并补充脚注与数据可用性说明。

深度因果估计的三种不同方法

深度学习文献中提出的因果估计架构均基于上述核心思想。首先，我们介绍“S学习器”和“T学习器”，以展示神经网络如何用于估计潜在结果中的非线性关系。其次，在正确的目标设定下，神经网络可学习处理组和控制组分布的去混杂表示（图3）。这种方法在理论上可与非参数匹配关联，下文“结合IPW的双重稳健性”部分将以基础算法TARNet为例进行说明（Shalit、Johansson和Sontag, 2017）。最后，机器学习因果推断文献的发展在很大程度上依赖于半参数框架的引入，该框架允许将预测性机器学习模型插入双重稳健估计方程（Van der Laan和Rose, 2011；Chernozhukov等, 2018, 2021）。在“结合IPW的双重稳健性”部分，我们将引入影响函数和靶向最大似然估计（TMLE）的概念，以解释Dragonnet算法。为清晰起见，本文介绍的算法均与TARNet算法有一定关联，但需注意，深度学习用于因果推断的方法还有很多（如在线附录中描述的生成模型）。

深度结果建模

S学习器与T学习器

由于每个单元最多只有一个潜在结果可观测，无法直接应用监督模型学习处理效应。在计量经济学、生物统计学和机器学习领域，应对这一挑战的常用方法是改用机器学习分别对每个潜在结果建模，并使用插入估计器计算处理效应（Chernozhukov等, 2018；Van der Laan和Rose, 2011；Wager和Athey, 2018）。与线性模型类似，可训练单个神经模型学习两个潜在结果（S[ingle]-学习器）（图1B），或训练两个独立模型分别学习每个潜在结果（“T-学习器”）（Johansson等, 2020）（图5A）。在这两种情况下，神经网络估计器均为前馈网络，其目标是最小化观测结果预测的MSE（均方误差）。不失一般性，T学习器的联合损失函数可表示为：
$$\mathcal{L}(Y,h(X,T))=\text{MSE}\left[Y_i,T_i\times h_1(X_i,1)+(1-T_i)\times h_0(X_i,0)\right]\text{\hspace{1em}(3)}$$
其中，$h_1$ 和 $h_0$ 分别表示对应两个潜在结果的独立网络。

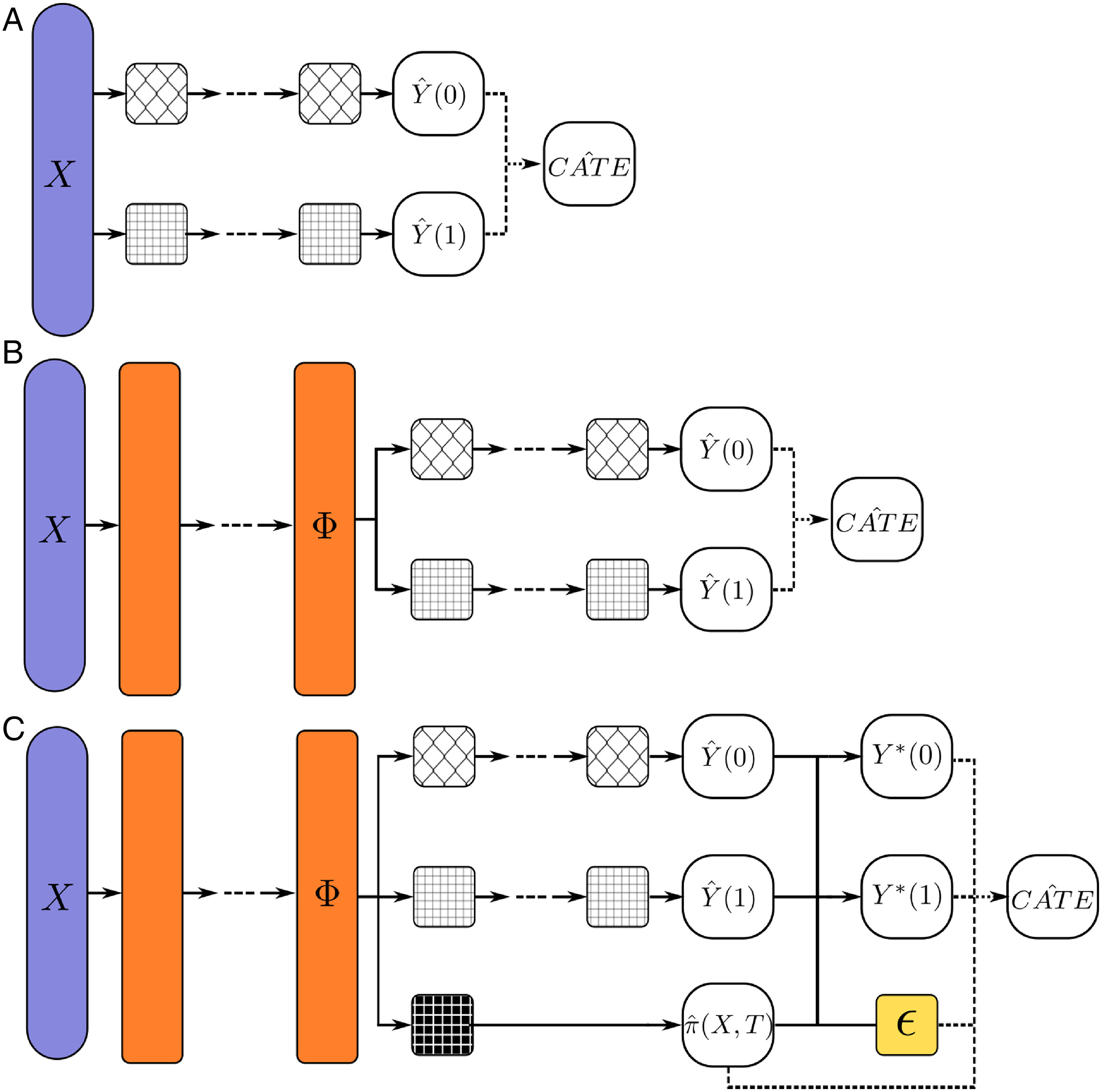
图5. （A）T学习器：在T学习器中，使用独立的前馈网络对每个结果建模（圆形白色框）。我们用 $h$ 表示这些结果建模器编码的函数。（B）TARNet：TARNet在T学习器的基础上增加了共享表示层（橙色）。TARNet（及该模型的进一步扩展）的设计动机是：准确预测处理组和控制组潜在结果的多任务目标，迫使表示层学习平衡函数 $\Phi$，使得表示空间中 $\Phi (X\mid T=0)$ 和 $\Phi (X\mid T=1)$ 的分布具有重叠性。代码实现见框7。（C）Dragonnet：Dragonnet在TARNet的基础上增加了倾向得分头（黑色纹理框）和一个自由“微调”参数 $ϵ$。通过改编靶向最大似然估计（TMLE），利用 $\hat{\pi }$ 和 $ϵ$ 对结果进行加权，以获得偏差更小的ATE估计。

训练完成后，将同一单元输入T学习器的两个网络，可得到两个潜在结果的预测值：$\hat{Y}(T)$ 和 $\hat{Y}(1-T)$。我们可将这些预测值插入以估计每个单元的CATE：
$${\hat{\tau }}_i=(1-2T_i)({\hat{Y}}_i(1-T_i)-{\hat{Y}}_i(T_i))$$
其中，第一项是一个切换项，确保处理组潜在结果排在前面。ATE的估计式为：
$$\widehat{\text{ATE}}=\frac{1}{N}\sum _{i=1}^N{\hat{\tau }}_i$$

下文描述的几乎所有模型，均将这种插入式结果建模方法与其他处理调整形式相结合。

通过表示学习实现平衡

TARNet

平衡是一种处理调整策略，旨在通过迫使处理组和控制组的协变量分布更接近，来消除处理与结果之间的混杂（Johansson、Shalit和Sontag, 2016）。深度学习对可观测选择文献的创新性贡献在于：提出神经网络可将协变量转换到表示空间 $\Phi$，使得处理组和控制组的协变量分布在该空间中无法区分（图3）。

为促使神经网络学习平衡表示，该领域的开创性文献（Shalit、Johansson和Sontag, 2017）提出了一种简单的双头神经网络TARNet，它在结果建模T学习器的基础上增加了共享表示层（图5B）。每个头对应一个潜在结果的建模：一个头学习函数 $\hat{Y}(1)=h_1(\Phi (X),1)$，另一个头学习函数 $\hat{Y}(0)=h_0(\Phi (X),0)$。训练过程中，同一时间只有一个头会接收误差梯度（即预测观测结果的头），但两个头都会将梯度反向传播到学习 $\Phi (X)$ 的共享表示层。其核心思想是：这些表示层必须学习平衡数据，因为它们需要同时为两个结果建模。该算法的作者随后对TARNet进行了扩展，增加了额外的损失函数，提出了CFRNet算法——通过最小化表示空间中两个协变量分布的统计距离，明确促进平衡；详见在线附录（Johansson等, 2018, 2020）。

该网络的完整目标是，拟合训练样本中所有 $n$ 个单元的 $h$ 和 $\Phi$ 参数，使得：
$$\arg \underset{h,\Phi }{\min }\frac{1}{N}\sum _{i=1}^N{\left[Y_i-\left(T_i\left[\underset{{\hat{Y}}_i(1)}{\underbrace{h_1(\Phi (X_i),1)}}\right]-(1-T_i)\left[\underset{{\hat{Y}}_i(0)}{\underbrace{h_0(\Phi (X_i),0)}}\right]\right)\right]}^2+\underset{\text{L2正则化}}{\underbrace{\lambda R(h)}}\text{\hspace{1em}(4)}$$
或更简洁地表示为：
$$\arg \underset{h,\Phi }{\min }\text{MSE}\left(Y_i,\underset{{\hat{Y}}_i(T_i)}{\underbrace{h(\Phi (X_i),T_i)}}\right)+\underset{\text{L2正则化}}{\underbrace{\lambda R(h)}}\text{\hspace{1em}(5)}$$
其中，$R(h)$ 是模型复杂度项（如用于L2正则化），$\lambda$ 是通过模型选择确定的超参数。TARNet在TensorFlow和PyTorch中的代码实现见框7。

框7：TARNet代码实现
下文展示了TARNet在Python TensorFlow 2和PyTorch中的简单实现。如需了解该实现的更多解释，或在IHDP数据上运行此代码，请参考教程。

TensorFlow 2函数式API（Keras）

def make_tarnet(input_dim):# 参数input_dim为X协变量的数量x = Input(shape=(input_dim,), name='input')# 在TF函数式API中，通过将前一层的输出传入下一层来堆叠网络层# 构建2个表示层# units为层的输出维度# elu为"指数线性单元"激活函数phi = Dense(units=200, activation='elu')(x)phi = Dense(units=200, activation='elu')(phi)# 开始构建独立的结果建模头y0_hidden = Dense(units=100, activation='elu')(phi)y1_hidden = Dense(units=100, activation='elu')(phi)# 添加第二层y0_hidden = Dense(units=100, activation='elu')(y0_hidden)y1_hidden = Dense(units=100, activation='elu')(y1_hidden)# 输出预测结果y0_pred = Dense(units=1, activation=None)(y0_hidden)y1_pred = Dense(units=1, activation=None)(y1_hidden)# 合并输出concat_pred = Concatenate(axis=1)([y0_pred, y1_pred])# 实例化模型model = Model(inputs=x, outputs=concat_pred)return model

PyTorch

import torch
import torch.nn as nnclass TARNet(nn.Module):def __init__(self, input_dim):super(TARNet, self).__init__()# 表示层self.phi = nn.Sequential(# PyTorch中需指定输入和输出维度nn.Linear(input_dim, 200),nn.ELU(),  # 激活函数与层分开定义nn.Linear(200, 200),nn.ELU())# 处理组结果建模隐藏层self.y0_hidden = nn.Sequential(nn.Linear(200, 100),nn.ELU(),nn.Linear(100, 100),nn.ELU())# 控制组结果建模隐藏层self.y1_hidden = nn.Sequential(nn.Linear(200, 100),nn.ELU(),nn.Linear(100, 100),nn.ELU())# 结果预测层self.y0_pred = nn.Linear(100, 1)self.y1_pred = nn.Linear(100, 1)# PyTorch中需在forward函数中定义数据/梯度的流动def forward(self, X):rep = self.phi(X)y0_rep = self.y0_hidden(rep)y0_hat = self.y0_pred(y0_rep)y1_rep = self.y1_hidden(rep)y1_hat = self.y1_pred(y1_rep)return y0_hat, y1_hat

结合IPW的双重稳健性

与直接对表示函数施加损失不同，IPW方法通过函数 $\pi (\Phi (X),T)=P(T\mid \Phi (X))$ 从表示中估计倾向得分。与传统IPW估计器类似，这类方法利用设定正确的倾向得分的充分性，对插入式结果预测进行加权，从而提供ATE的无偏估计（Rosenbaum和Rubin, 1983）。由于这些模型结合了结果建模与IPW，因此保留了“处理建模：非参数匹配”部分讨论的双重稳健估计器的优良统计性质（Atan、Jordon和Schaar, 2018）。本节将重点介绍Shi、Blei和Veitch（2019）提出的Dragonnet模型，该模型将半参数估计理论适配于神经网络的批次训练，提出了“靶向正则化（TarReg）”方法（Kennedy, 2016）。鉴于半参数理论和“双重机器学习”在因果估计文献中的重要性日益提升，在深入介绍Dragonnet算法细节之前，我们先简要引入半参数理论和靶向最大似然估计（TMLE）的概念（Van der Laan和Rose, 2011；Chernozhukov等, 2018）。

Dragonnet

对TARNet的一个简单扩展是增加第三个头以预测倾向得分。正如Dragonnet所提出的，这个第三头可以使用多个神经网络层，也可以仅使用单个神经元（图5C）（Shi、Blei和Veitch, 2019）。Dragonnet利用这个额外的头，借鉴TMLE（Van der Laan和Rose, 2011）的思想，开发了用于半参数因果估计的“靶向正则化”训练方法。

对于具有三个头的网络，其基本损失函数为：
$$\arg \underset{h,\Phi ,\pi }{\min }\underset{\text{结果损失}}{\underbrace{\text{MSE}\left(Y_i,\underset{\text{结果损失}}{\underbrace{h(\Phi (X_i),T_i)}}\right)}}+\alpha \underset{\pi 损失}{\underbrace{\text{BCE}\left(T_i,\pi (\Phi (X_i),T_i)\right)}}+\underset{\text{L2正则化}}{\underbrace{\lambda R(h)}}\text{\hspace{1em}(6)}$$
其中，$\alpha$ 是平衡两个目标的超参数，$\lambda$ 是平衡目标与模型复杂度项的超参数。均方误差（MSE）和二元交叉熵（BCE）分别是机器学习中回归和二元分类的标准目标函数。需注意，第一项与式（5）的第一项相同。

下文将探讨作者如何在上述损失函数的基础上增加第二个损失，以实现半参数估计。

因果推断的半参数理论

近年来，半参数理论已成为将包括神经网络在内的机器学习算法应用于因果估计的主导理论框架（Chernozhukov等, 2018, 2021, 2022；Farrell、Liang和Misra, 2021；Kennedy, 2016；Nie和Wager, 2021；Van der Laan和Rose, 2011；Wager和Athey, 2018）。这类框架的巨大吸引力在于：它们允许将机器学习算法用于结果和倾向得分的非线性估计，同时仍能提供优良的统计保证（如一致性、有效性、渐近有效的置信区间）。

从直观层面看，半参数因果估计的核心是估计处理效应分布 $P$ 的目标参数 $T(P)$（即估计ATE）（Fisher和Kennedy, 2021）。由于缺乏反事实数据，我们无法得知处理效应的真实分布，但我们知道该分布的一些参数（如处理分配机制）。我们可以将这些约束编码为似然函数，该函数从参数上定义了一组基于现有数据的可能近似分布 $P$。在这组分布中，存在一个由样本推断的分布 $\tilde{P}\in P$，可用于通过 $T(\tilde{P})$ 估计 $T(P)$。

无论选择何种 $\tilde{P}$，都有 $\tilde{P}\ne P\to T(\tilde{P})\ne T(P)$。我们无法确定在有限数据下选择何种 $\tilde{P}$ 能得到 $T(\tilde{P})$ 的最佳估计。我们可以通过最大化似然函数来选择 $\tilde{P}$，但似然函数中可能存在非目标的“干扰参数”，我们并不关心这些参数的准确估计。最大似然优化可能会以牺牲 $T(P)$ 的估计精度为代价，降低这些干扰项的偏差。

为使似然函数更聚焦于 $T(P)$，我们定义一个“微调”参数 $ϵ$：从 $\tilde{P}$ 出发，在 $P$ 中选择 $T({\tilde{P}}_{ϵ})$，使其更接近 $T(P)$。$T(P)$ 的影响函数描述了 $ϵ$ 的变化如何导致 $T({\tilde{P}}_{ϵ})$ 的变化。我们将利用这个影响函数拟合 $ϵ$，以在似然框架内更好地近似 $T(P)$。具体而言，存在一种特殊的有效影响函数（EIC），可提供 $T(P)$ 的最小方差估计。在因果估计中，求解ATE的EIC可得到渐近无偏、有效且置信区间（渐近）覆盖正确的估计。

ATE的EIC为：
$${\text{EIC}}_{\text{ATE}}=\frac{1}{N}\sum _{i=1}^N\left[\underset{\text{调整项}}{\underbrace{\underset{\text{处理建模}}{\underbrace{\left(\frac{T_i}{\pi (X_i,1)}-\frac{1-T_i}{\pi (X_i,0)}\right)}}\times \underset{\text{残差混杂}}{\underbrace{\left(Y_i-h(X_i,T_i)\right)}}}}+\underset{\text{结果建模}}{\underbrace{\left(h(X_i,1)-h(X_i,0)\right)}}\right]-\text{ATE}\text{\hspace{1em}(7)}$$

令 ${\text{EIC}}_{\text{ATE}}$ 的均值为0，可得：
$$\text{ATE}=\frac{1}{N}\sum _{i=1}^N\left[\underset{\text{调整项}}{\underbrace{\underset{\text{处理建模}}{\underbrace{\left(\frac{T_i}{\pi (X_i,1)}-\frac{1-T_i}{\pi (X_i,0)}\right)}}\times \underset{\text{残差混杂}}{\underbrace{\left(Y_i-h(X_i,T)\right)}}}}+\underset{\text{结果建模}}{\underbrace{\left(h(X_i,1)-h(X_i,0)\right)}}\right]\text{\hspace{1em}(8)}$$

下划线标注表明，${\text{EIC}}_{\text{ATE}}$ 与双重稳健估计器类似。当如式（8）所示将EIC最小化（设为0）时，ATE等于结果建模估计加上与残差误差成比例的处理建模估计。

从TMLE到靶向正则化

靶向正则化（TarReg）的设计紧密借鉴了靶向最大似然估计（TMLE）（Van der Laan和Rose, 2011）。TMLE是一种迭代过程，其中干扰参数 $ϵ$ 用于在最小化式（8）中的EIC时，将结果模型微调至更精确的ATE估计[11]。其步骤如下：

1. 拟合 $h$：通过预测结果（如使用TARNet）并最小化 $\text{MSE}(Y_i,h(\Phi (X_i),T_i))$；
2. 拟合 $\pi$：通过预测处理（如使用逻辑回归）并最小化 $\text{BCE}(T_i,\pi (\Phi (X_i),T_i))$；
3. 插入 $h$ 和 $\pi$ 函数以拟合 $ϵ$，并估计 $h^{\ast }(X,T)$，其中：
   KaTeX parse error: Got function '\hat' with no arguments as superscript at position 71: …X_i), T_i)}_{Y^\̲h̲a̲t̲{}} + \underbra…
   拟合方式为最小化 $\text{MSE}(Y,h^{\ast }(\Phi (X),T))$，这等价于最小化式（8）中的“调整项”；
4. 插入 $h^{\ast }(X,T)$ 以估计 $\widehat{\text{ATE}}$：
   $${\widehat{\text{ATE}}}_{\text{TMLE}}=\frac{1}{N}\sum _{i=1}^N\left(\underset{Y_i^{\ast }(1)}{\underbrace{h^{\ast }(X_i,1)}}-\underset{Y_i^{\ast }(0)}{\underbrace{h^{\ast }(X_i,0)}}\right)$$

靶向正则化借鉴TMLE并将其适配为神经网络损失函数。主要区别在于：上述步骤1和2由Dragonnet同时完成，且前三个步骤的损失函数被合并为单个损失，在每个批次结束时应用于整个网络。这需要在Dragonnet网络中为 $ϵ$ 添加一个自由参数。

从直观层面看，靶向正则化的吸引力在于：它为TARNet引入了一个损失函数，明确促使网络学习处理效应分布的均值，而非仅学习结果分布。靶向正则化的过程如下：

在每个epoch中：

1. a. 使用Dragonnet预测 $h(\Phi (X),T)$ 和 $\pi (\Phi (X),T)$；
   b. 使用超参数 $\alpha$ 计算网络的标准机器学习损失：
   $$\arg \underset{h,\Phi ,\pi }{\min }\underset{\text{结果损失}}{\underbrace{\text{MSE}(Y_i,h(\Phi (X_i),T_i))}}+\alpha \underset{\pi 损失}{\underbrace{\text{BCE}(T_i,\pi (\Phi (X_i),T_i))}}+\underset{\text{L2正则化}}{\underbrace{\lambda R(h)}}$$
2. a. 按上述方式计算 $h^{\ast }(\Phi (X_i),T_i)$：
   KaTeX parse error: Got function '\hat' with no arguments as superscript at position 80: …X_i), T_i)}_{Y^\̲h̲a̲t̲{}} + \underbra…
   b. 计算靶向正则化损失：$\text{MSE}(Y,h^{\ast }(\Phi (X),T))$；
3. 使用超参数 $\beta$ 合并并最小化步骤1和2的损失：
   $$\arg \underset{\Phi ,h,ϵ}{\min }\underset{\text{结果损失}}{\underbrace{\text{MSE}\left[Y_i,h(\Phi (X_i),T_i)\right]}}+\alpha \cdot \underset{\pi 损失}{\underbrace{\text{BCE}\left[T_i,\pi (\Phi (X_i),T_i)\right]}}+\underset{\text{L2正则化}}{\underbrace{\lambda R(h)}}+\beta \cdot \underset{\text{靶向正则化损失}}{\underbrace{\text{MSE}(Y_i,h^{\ast }(\Phi (X_i),T_i))}}$$

靶向正则化的步骤3完全等价于将EIC最小化（至多相差一个常数 $\beta$）。

因此，训练结束后，我们可以像TMLE一样估计ATE的靶向正则化估计 ${\widehat{\text{ATE}}}_{\text{TR}}$：
$${\widehat{\text{ATE}}}_{\text{TR}}=\frac{1}{N}\sum _{i=1}^N\left(\underset{Y_i^{\ast }(1)}{\underbrace{h^{\ast }(\Phi (X_i),1)}}-\underset{Y_i^{\ast }(0)}{\underbrace{h^{\ast }(\Phi (X_i),0)}}\right)$$

与S学习器、T学习器和TARNet相比，Dragonnet算法的特别吸引力在于其半参数框架提供的统计保证：它具有双重稳健性、无偏性，收敛速度为 $\frac{1}{\sqrt{n}}$，且抽样分布渐近正态。下文将介绍如何为该估计器构建渐近有效的置信区间。

置信度与解释

本节将从理论转向实践，探讨构建置信区间和解释异质性处理效应的最佳实践。这两个主题不仅在因果推断文献中，而且在整个机器学习研究中都是活跃发展的领域。此处我们特别聚焦于分析师可轻松实现的建议。

置信度评估

本文重点介绍Dragonnet而非其他方法，正是因为它具有优良的统计性质。由于Dragonnet中的靶向正则化过程本质上是TMLE的一种变体，因此可将EIC的样本校正方差 ${\hat{\sigma }}_{\text{ATE}}$ 作为渐近有效的标准误，其中：
$${\hat{\sigma }}_{{\text{ATE}}_{\text{TR}}}=\frac{\text{Var}({\text{EIC}}_{{\text{ATE}}_{\text{TR}}})}{N}\text{\hspace{1em}(9)}$$
且：
$$\text{Var}({\text{EIC}}_{{\text{ATE}}_{\text{TR}}})=\text{Var}\left[\left(\frac{T_i}{\pi (X_i,1)}-\frac{1-T_i}{\pi (X_i,0)}\right)(Y-h^{\ast }(X_i,T_i))+(h^{\ast }(X_i,1)-h^{\ast }(X_i,0))-{\widehat{\text{ATE}}}_{\text{TR}}\right]\text{\hspace{1em}(10)}$$
（Van der Laan和Rose, 2011, p. 96）

教程4展示了如何使用 ${\hat{\sigma }}_{\text{ATE}}$ 计算Dragonnet的Wald置信区间。尽管本文未重点介绍，但也可使用RieszNet（Dragonnet的一种变体，由Chernozhukov等（2022）提出）计算渐近有效的置信区间。RieszNet将神经网络估计与当前因果计量经济学中流行的自动去偏机器学习文献联系起来（Chernozhukov等, 2018, 2021）。

解释性

缺乏可解释性一直是神经网络、随机森林等机器学习方法在社会科学领域应用的障碍。然而，过去五年中，事后解释技术的文献已大幅成熟，如今多种用于识别重要特征/协变量的技术（如置换重要性、LIME得分、SHapley可加解释（SHAP）得分、个体条件期望图等）已被广泛使用（Altmann等, 2010；Goldstein等, 2015；Lundberg和Lee, 2017；Ribeiro、Singh和Guestrin, 2016）。有关解释机器学习模型的广泛且易懂的论述，请参见Molnar（2022）。

基于评估其他可解释AI方法的标准，Crabbé等（2022）指出，用于解释深度因果估计器的特征重要性技术应具备四个理想性质：敏感性、完整性、线性和实现不变性（Sundararajan、Taly和Yan, 2017）。具有敏感性的方法能够区分仅预测结果的特征和实际影响CATE异质性的特征；具有完整性的方法能够识别所有特征，这些特征共同解释了相对于基准的所有效应异质性；线性方法的特征重要性得分可加性地描述预测；最后，该方法应与模型架构（如TARNet、Dragonnet）和不同的架构超参数化无关（即实现不变性）。在综述的特征重要性方法中，他们发现两种方法具备所有这四个性质：SHAP得分和集成梯度。

SHAP得分近年来已成为评估机器学习模型最流行的方法之一（Lundberg和Lee, 2017）。SHAP属于“局部”解释方法：它为每个单独的数据点提供特征重要性估计。理论上，SHAP将特征重要性估计视为协变量之间的合作（博弈论）博弈，目标是预测特定结果。该算法会详尽比较协变量的所有可能“联盟”及其预测结果（赢得博弈）的能力，并利用这些联盟预测的幂集，通过Shapley值计算每个特征在预测中的可加边际贡献。SHAP的缺点是，即使采用计算技巧，在高维数据集中为每个单元计算得分也可能在计算上难以实现。SHAP得分的解释需基于ATE的因果基准进行比较。

由于SHAP得分的计算成本较高，Crabbé等（2022）还推荐另一种局部解释方法——“集成梯度”（Sundararajan、Taly和Yan, 2017）。直观而言，该算法在特征空间中绘制一条从目标输入（单个单元）到基准（即所有协变量均为平均值的假设单元）的直线线性路径。然后，通过计算该路径上预测误差相对于目标特征的梯度，构建特征重要性得分。需注意，从理论上也可在路径框架内理解SHAP得分：从这个角度看，联盟是依次激活每个特征的路径，而SHAP得分是这些路径的期望。这种解释引出了一种专为神经网络计算SHAP得分的基于梯度的算法，该算法也包含在SHAP软件包中。在实践中，我们建议分析师同时尝试集成梯度和SHAP得分。

教程包含哪些内容？

为从理论转向实证，在线教程展示了如何实现本入门读物中介绍的许多思想。教程以Google Colaboratory环境中的笔记本形式提供：用户打开Colab笔记本后，Google会立即提供一个免费虚拟机，其中包含标准的Python机器学习包。这意味着读者无需在自己的计算机上安装任何软件，即可尝试这些模型。教程使用Python编程语言编写，并提供TensorFlow 2和PyTorch（两种最流行的深度学习框架）的示例。需注意，TensorFlow 2和PyTorch均有R语言实现，但我们强烈建议希望深入学习深度学习的读者使用Python——它拥有更丰富的机器学习第三方包生态系统。

目前共有五个教程：

• 教程1：先介绍S学习器和T学习器，再介绍TARNet，帮助读者熟悉如何构建自定义TensorFlow模型。
• 教程2：聚焦因果推断指标和超参数优化。由于无法观测反事实结果，如何为因果推断优化监督学习模型并不直观。本教程介绍了一些评估模型性能的指标：第一部分教读者如何在TensorBoard中评估这些指标的性能；第二部分通过修改Keras Tuner实现TARNet的超参数优化，并讨论将模型作为估计器而非预测器进行训练的注意事项。
• 教程3：重点介绍Shi、Blei和Veitch（2019）提出的TARNet半参数扩展。我们在TARNet模型中添加处理建模，构建增强逆倾向得分估计器；随后简要介绍靶向最大似然估计（TMLE）算法，以引入并构建带有Shi等人靶向正则化的Dragonnet。
• 教程4：在PyTorch中重新实现Dragonnet，并展示如何计算ATE的渐近有效置信区间；同时使用集成梯度和SHAP得分解释对不同异质性CATE有贡献的特征。即使不考虑因果推断背景，仅希望学习如何解释SHAP得分的读者，也会发现本教程很有帮助。
• 教程5：介绍Shalit、Johansson和Sontag（2017）以及Johansson等（2018, 2020）提出的反事实回归网络（CFRNet）和倾向加权CFRNet（见在线附录）。该方法利用积分概率度量绑定反事实预测损失，迫使处理组和控制组分布更接近；加权变体添加了基于倾向的自适应权重，提供一致性保证、放宽重叠假设，并有望降低偏差。

超越传统数据：文本、网络、图像与随时间变化的处理

尽管神经网络在从定量数据估计异质性处理效应方面已十分令人兴奋，但深度因果估计的一大前景在于：当处理、混杂因素和中介变量编码在高维数据（如文本、图像、社交网络、语音和视频）中或呈时变特征时，仍能进行推断。这是神经网络相对于其他机器学习方法的显著优势——其他方法在非定量数据上的泛化性能无法与之竞争。在这些场景中，可利用多任务目标和定制化架构学习表示：这些表示既丰富，又能捕捉因果量的信息，并解开它们之间的关系。此外，神经网络固有的灵活性意味着，在许多情况下，上述TARNet类模型只需进行一些架构修改、添加额外损失和引入新的识别假设，即可作为文本和图形推断的基础。

该领域的文献正在迅速发展，因此读者应将本入门读物的本节视为具有前瞻性的内容。为保持可理解性，此处的主要目标是向读者介绍可能对文本、网络或图像数据进行因果推断的假设场景；其次，选择性综述该领域中关于深度因果估计的当代理论驱动文献（不同数据类型的识别假设差异很大，因此我们通常将其留给感兴趣的读者深入探索）；最后，简要讨论处理时变混杂的方法。本节还将介绍图神经网络（GNN）和Transformer架构——目前大多数当代深度学习模型均使用这两种架构从复杂数据中学习（框8）。

---

框8：图神经网络与Transformer

图神经网络（GNN）

图神经网络（GNN）是当前为图中节点创建表示的最先进方法。与以往仅基于节点局部上下文（如向邻近节点的随机游走）构建“浅层”嵌入的方法相比，GNN的优势在于：其节点表示是从目标节点的 $n$ 阶邻居（即与目标节点相隔 $n$ 步的所有节点）的结构位置和协变量中聚合而来，其中 $n$ 是图神经网络的层数。

理解图神经网络工作原理的最直观方式是将其视为一种消息传递系统（Gilmer等, 2017）。我们以最早的GNN论文之一——图卷积网络（GCN）为例（Kipf和Welling, 2017）。在这种解释中，每个节点都有一条消息，通过图卷积操作传递给其邻居：GNN第一层的消息由节点的协变量/特征组成；在后续层中，这些消息实际上是前一层产生的节点表示。图卷积过程中，每个节点将传入的消息与其自身的权重集相乘，并使用聚合函数（如求和）组合这些加权输入。到第 $n$ 层GNN时，这些消息将包含所有 $n$ 阶邻居节点的结构和协变量信息。对于感兴趣的读者，该过程还有谱域解释。通常，GNN通过预测两个节点在网络中相连的概率来学习图的表示，随后将其用于其他任务。GNN的一种变体使用“注意力”机制，使节点能够不同程度地重视来自不同邻居的消息（即图注意力网络GAT）（Veličković等, 2018）。

Transformer

截至2023年，Transformer仍是自然语言处理（NLP）中占主导地位的架构。自2017年推出以来，这些模型全面提升了许多高关注度NLP任务的性能。一些企业级Transformer因其在文本生成和问答方面的出色表现而受到媒体关注（如OpenAI的GPT-3/4、Google的Bard、Meta的Llamma）；广泛使用的较小模型则基于BERT架构（Devlin等, 2019）。

Transformer和GNN（尤其是GAT）在架构上大致等价。从图的角度看，句子中的单词类似于网络中的节点，单词之间的相对位置类似于它们在图中的结构位置。与以往的文本分析序列方法（如循环神经网络）不同，Transformer的每个单词（或单词表示）不仅接收相邻单词的消息，还能异质地接收所有单词的消息。架构中的注意力机制使Transformer的每一层都能异质地关注单词或聚合表示。BERT或GPT等架构通过堆叠Transformer层，构建出具有数亿至数千亿参数的模型。这些模型的训练成本（计算和数据方面）很高，因此通常在海量数据集上进行预训练，然后使用较小的数据集进行“微调”（轻度再训练），以适应特定任务或目标。

---

基于文本的因果推断

近年来，社会科学和计算机科学领域的跨学科团队围绕基于文本的因果推断开展了大量研究（详见Keith、Jensen和O’Connor（2020）以及Feder等（2021）的综述）。广义而言，文本可捕捉我们感兴趣的任何因果量（处理、结果、混杂因素、中介变量）的信息。例如，在退出投票实验中，分析师可能希望测量文本对政治提示的响应中的毒性（Y）；在电子邮件响应时间（Y）的观察性研究中，分析师可能希望测量电子邮件语气（T）的效应——在这种场景中，分析师可能还希望控制主题（X）等混杂因素。每种场景都面临独特的识别挑战（Feder等, 2021），但在所有情况下，我们都可以使用高维文本的低维表示，提取、量化并解开语气、主题等细微特征之间的关系。

神经网络的自动特征提取能力使其特别适合以下场景：处理信息和混杂协变量均编码在文本中。在许多情况下，我们可能未明确识别、量化或标记文本中的所有混杂因素（如电子邮件的主题和语气），但仍希望对其进行控制。Pryzant等（2021）、Veitch、Sridhar和Blei（2020）以及Gui和Veitch（2022）通过在TARNet或Dragonnet的开头添加用于读取文本的Transformer层（框8），解决了这一问题。Veitch、Sridhar和Blei（2020）在一项“科学学”问题中验证了该方法的可行性——该问题旨在测试公式对计算机科学会议论文录用的因果效应。Pryzant等（2021）、Gui和Veitch（2022）则探索了更复杂的场景：处理并非明确已知（如论文中的公式、作者性别），而是通过阅读文本间接感知的（如电子邮件的礼貌/粗鲁程度或社交媒体帖子的毒性）。在这些模型中，除上述因果推断损失外，还添加了一个额外的损失函数，用于同时学习文本表示。

基于网络的因果推断

利用关系数据进行因果推断的文献较少，主要集中在两种不同场景：

第一种是传统的可观测选择场景：我们希望控制从同质性连接中可推断出的未观测混杂信息。例如，数据中可能未测量年龄或性别，但我们可预期人们会与同性或同龄群体建立友谊关系。

这种场景表明，其估计策略与混杂因素编码在文本中的场景类似。正如可在TARNet类估计器前添加Transformer层以从文本中学习一样，也可添加GNN（Transformer的类似物）以从图形中学习。Guo、Li和Liu（2020）首次尝试解决这一问题，在CFRNet（Shalit、Johansson和Sontag, 2017）中添加了GNN层（框8）。Veitch、Wang和Blei（2019）则在半参数框架中改编Dragonnet，假设网络表示包含混杂因素的重要信息，从而实现处理和结果的一致估计。

第二种更具挑战性的场景是：从观察性数据中估计社会影响对结果的因果效应。例如，Cristali和Veitch（2022）提出了测量疫苗接种（T）对同伴疫苗接种选择（Y）的效应这一问题。这是一个难题，原因有二：（a）稳定单元处理值假设（SUTVA）是所有因果推断框架的基本假设；（b）难以区分结果变化是源于处理的同伴效应（如A说服B接种疫苗），还是源于同质性（如A和B具有相似的政治倾向）。换言之，传播和同质性通常存在混杂（Shalizi和Thomas, 2011）。McFowland和Shalizi（2023）首次尝试解决这一问题，他们对网络连接的生成和结果模型做出了强参数假设；Cristali和Veitch（2022）则提出了一种使用神经网络学习图形表示的方法。

基于图像的因果推断

尽管因果推断的思想已被广泛用于改进图像分类，但据我们所知，目前尚无研究探索处理、混杂因素、中介变量或预测变量编码在图像中的因果推断[12]。尽管如此，用于文本因果分析的一些场景在此处也应适用。例如，考虑Todorov等（2005）开展的关于政治家面部当选可能性的联合实验——实验中，处理（如政治家的现任身份）和潜在的潜在混杂因素（如政党、年龄、性别、种族）均编码在图像中。在这种场景中，经适配以学习图像表示并基于其进行条件推断的TARNet类模型，可通过控制政治家年龄等混杂因素，改进处理效应估计。基于图像的因果推断是一个亟待探索的领域，我们期待未来能看到更多相关研究。

基于时变数据的因果推断

深度因果估计的一个自然扩展是处理随时间实施且混杂可能呈时变特征的场景。尽管Robins等人提出的用于估计时变处理和混杂效应的“g方法”已存在数十年，但这些模型中编码的统计假设非常严格（Robins, 1994；Robins和Hernán, 2008；Robins、Hernan和Brumback, 2000）：首先，由于依赖广义线性模型定义“结构”部分，它们假设结果是所有协变量和处理的线性函数；其次，为实现识别，需对哪些先前时间步会混杂当前时间步做出强假设；最后，需在每个时间步估计不同的系数。Transformer（框8）和循环神经网络（RNN，一种更简单的序列数据模型，见在线附录）应能捕捉长期依赖关系和非线性特征，而这是边际结构模型和g计算无法实现的。

已有多篇论文开始在个性化医疗背景下探索这些可能性：Lim、Alaa和van der Schaar（2018）使用RNN构建边际结构模型；Bica等（2020）扩展了该框架，添加了额外的损失函数，通过迫使模型“遗忘”先前时间步的信息，更明确地处理时变混杂；Melnychuk、Frauen和Feuerriegel（2022）更进一步，在Bica等（2020）方法的基础上适配了Transformer；Frauen等（2022）受纵向靶向最大似然估计的启发，在RNN中添加了半参数靶向层，构建了具有双重稳健性和渐近有效性的g计算算法；Li等（2021）则提出了一种用于g计算的RNN框架，支持动态处理方案。所有这些论文均使用肿瘤生长动力学模拟、基于重症监护病房生命体征的自然模拟，或背痛对物理治疗响应的数据集。

结论：背景下的深度因果估计

本入门读物向社会科学家介绍了新兴的深度学习因果推断机器学习文献。为奠定基础，我们首先直观介绍了表示学习、多任务学习等深度学习基本概念，以及训练神经网络的实用指南。在文章主体部分，我们展示了机器学习研究者如何调整核心处理和结果建模策略，以利用神经网络在异质性处理效应估计中的独特优势。随后讨论了推断相关问题（如模型选择、置信区间、解释），最后对文本、社交网络、图像和时变数据的推断算法进行了前瞻性展望。

深度学习并非异质性处理效应推断的唯一潜在工具——计量经济学和生物统计学领域均有丰富文献探索其他方法的应用（Van der Laan和Rose, 2011；Chernozhukov等, 2018；Wager和Athey, 2018）。尽管这些文献无疑更成熟，但下文将讨论我们认为神经网络与其他机器学习方法之间应用差距将继续缩小的原因——我们必须为此做好准备。

首先，在建模非线性异质性（如处理响应中的异质性）方面，神经网络优于其他机器学习方法。Curth等（2021）的大量模拟表明，当处理异质性的数据生成过程包含指数关系时，神经网络的性能优于随机森林；但当数据生成过程基于线性函数时，树基方法更稳健。此外，在预测异常值处理效应方面，神经网络也始终优于森林。这些差异源于两种方法的函数建模方式：神经网络只需足够多的神经元即可逼近任何连续函数，而随机森林必须使用分段函数构建非线性或非正交决策边界，并对预测进行平均。与这些差异一致，Curth等（2021）还发现，当变量以连续协变量形式构建时，神经网络表现更好；而当变量被二分时，随机森林表现更优。

从统计角度看，半参数和双重机器学习框架的兴起也缩小了神经网络与其他类型机器学习在理论保证方面的差距。例如，本文重点介绍的受TMLE启发的Dragonnet算法具有无偏性、合理一致性，且以 $\frac{1}{\sqrt{n}}$ 的快速速率收敛到目标估计量。与之密切相关的Riezsnet双重机器学习模型（未重点介绍）也具有类似保证（Chernozhukov等, 2022）。除这些算法外，还存在一个不断发展的相邻文献——模型无关的插入学习器（如X学习器、R学习器），它们可利用神经网络的优势（Nie和Wager, 2021；Künzel等, 2019）。

第三，关于神经网络“数据饥渴”和“不可解释”的普遍看法被夸大了。当神经网络过度参数化或从图像等高维数据中学习时，确实需要大量数据；但我们在教程中表明，规模适中（数百个神经元）、正则化良好的神经网络，即使在少于800个单元的定量数据自然模拟中，也能成功推断异质性处理效应。在“置信度与解释”部分，我们还强调了过去五年机器学习可解释性的显著进展——其中许多是模型无关方法，对所有黑箱算法均同等有益。批评者常将袋外特征重要性视为随机森林的一大优势，但研究表明，这种方法的准确性终究不如模型无关的置换重要性（Altmann等, 2010）。

在我们看来，当前深度学习方法最紧迫的局限性在于优化神经网络的难度。从理论上讲，这源于两方面：（a）损失函数通常具有非凸性，复杂度较高；（b）这些模型很容易被过度参数化，从而拟合这些函数。若要将神经网络用作统计估计器，其统计保证必须有优化保证和/或更严格的模型选择方法作为支撑。在统计估计之外的领域，这一局限性在很大程度上已通过在测试数据上进行实证检验和策略性模型选择得到解决；但在统计估计场景下，这一差距可能需要通过基于模拟的敏感性分析来弥补，短期内则需通过与其他模型家族的比较来应对。

此外，这类模型的成熟工具和实证应用目前仍较为缺乏。本入门读物（尤其是教程）的一个主要目标是，将理论文献、实用训练与解释指南以及带注释的代码整合在一起，方便社会科学家开始使用这些模型。TensorFlow和PyTorch等深度学习框架的易用性逐年提升，但我们需指出，对于仅希望尝试其中部分模型的读者，已有现成的Python包可用（如优步的causalML）（Chen等, 2020）。

尽管存在当前的局限性，我们仍相信因果估计的未来离不开深度学习。随着因果推断进入新场景，神经网络的灵活性将成为从文本、图形、图像、视频和语音数据中学习的关键。在时变场景下，我们认为神经网络对非线性和长期时间依赖关系的建模能力，最终将催生出比现有方法假设更弱的解决方案。总体而言，我们对未来几年深度因果估计的发展持乐观态度，并对此充满期待。

脚注

1. 神经网络可包含数百至数十亿个参数，使其在实际应用中接近非参数模型。神经网络过度参数化的风险将在“深度学习基础”部分讨论。
2. 机器学习的另外两大主要范式是无监督学习和强化学习。
3. 需注意，统计学习理论中的“偏差”与统计估计器的“偏差”并非同一概念。
4. 若想了解从统计物理学角度对神经网络进行理论分析的相关研究，可参见Roberts、Yaida和Hanin（2022）。
5. 在因果推断的特定场景下，我们建议迷你批次的规模不宜过小，以确保模型能从具有足够重叠性的处理组和控制组单元中学习。
6. 在凸函数（如普通最小二乘损失）中，存在唯一的最小值，因此优化函数时总能收敛到相同的参数权重；但非凸函数则不同，它可能存在多个局部最小值。
7. 需注意，交叉拟合（Zivich和Breskin, 2021）是另一种用于其他类型机器学习因果估计器模型选择的方法，可能也适用于本文讨论的模型，但该方法很可能存在数据效率低的问题。
8. 对撞变量是指由另外两个变量共同导致的变量。控制对撞变量或对撞变量的后代，会在其“父变量”之间引入虚假相关性。在调整混杂的场景中，控制对撞变量可能会（重新）打开原本已阻断的混杂路径，从而引入额外偏差。
9. 另一种可用于估计结果的结果建模方法是g计算，本文未对此展开讨论（Robins, 1986；Hernán和Robins, 2020）。
10. 为降低稀疏数据导致的极端权重对估计结果的影响，有时会使用“稳定化”逆倾向得分加权（Glynn和Quinn, 2010）。
11. 若想深入了解靶向学习，建议参考Benkeser和Chambaz（2020）的研究。
12. Jesson等（2021）提出了一个模拟场景，将MNIST手写数字数据集作为协变量X，以此作为高维混杂的示例，但并未涉及实际应用。
13. 批评者常将袋外特征重要性视为随机森林的一大优势，但研究表明，这种方法的准确性终究不如模型无关的置换重要性（Altmann等, 2010）。

数据可用性声明

本教程使用Hill（2011）提出的IHDP自然模拟数据作为示例。该数据集包含747个单元（139个处理组单元）的25个协变量/特征，这些协变量/特征源自一项实验，但Hill通过模拟结果构建了已知的反事实数据。该数据可从Fredrik Johansson的网站获取：https://www.fredjo.com。