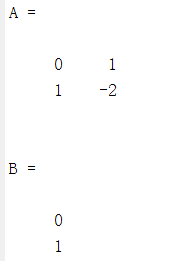【PID】基本PID控制 chaprt1 学习笔记

1 PID控制原理

PID控制器是一种线性控制器，常作为模拟控制系统中的控制器，根据给定值$y_d(t)$与实际输出值$y(t)$构成的控制偏差来进行控制。
$$err(t)=y_d(t)-y(t)$$
传递函数在零初始条件下被定义为系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比。

而在计算机系统中，我们需要采用离散化的方法，将模拟PID控制算法离散化：

• 用采样时刻点kT代替连续时间t
• 用矩阵法数值积分近似替代积分
• 用一阶向后差分近似替代微分

1.1 PID控制系统的基本结构 chapt1_1.mdl

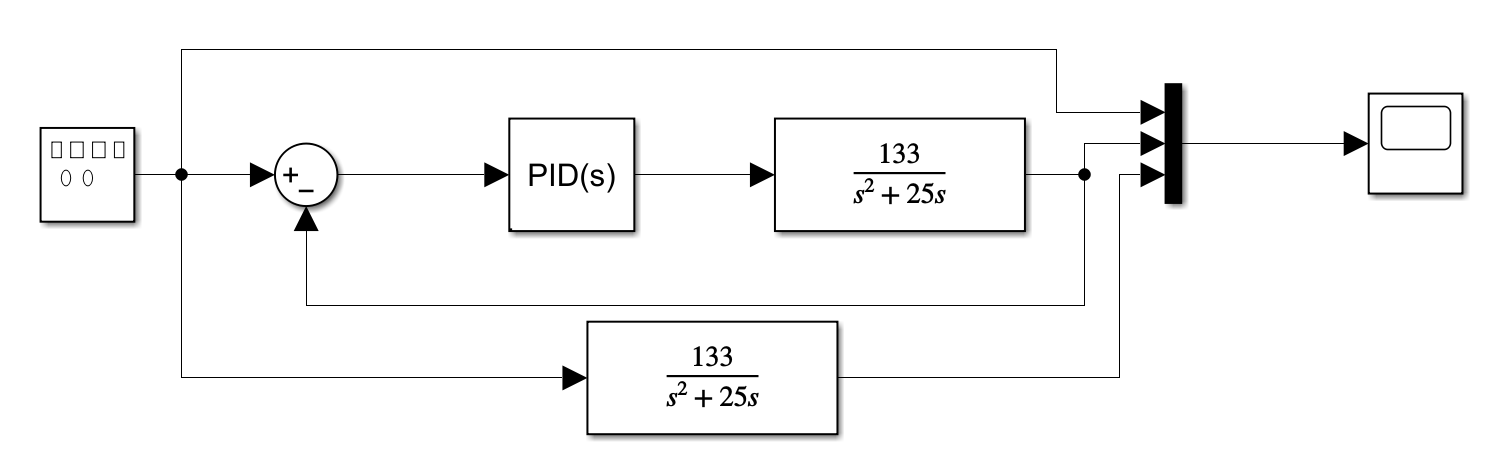
注意PID控制的目标，一般都是希望输出跟随控制量（或者两者符合某种函数关系）

此处我们调整的目标，是希望输入，经过一个系统（传函），其输入和输出曲线尽可能的重合。

看结果：


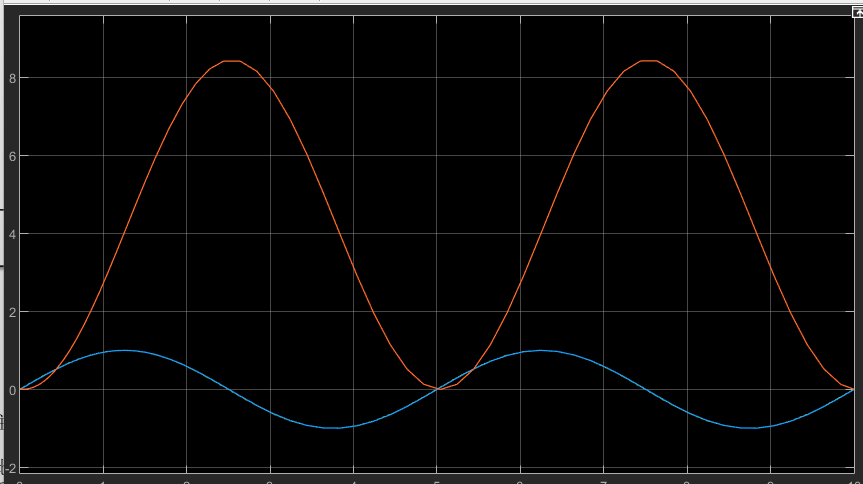
第二路PID（黄色曲线）基本跟随了第一路（期望输出），而第三路（未经过任何控制，直接输入给模型）则完全偏离第一路。

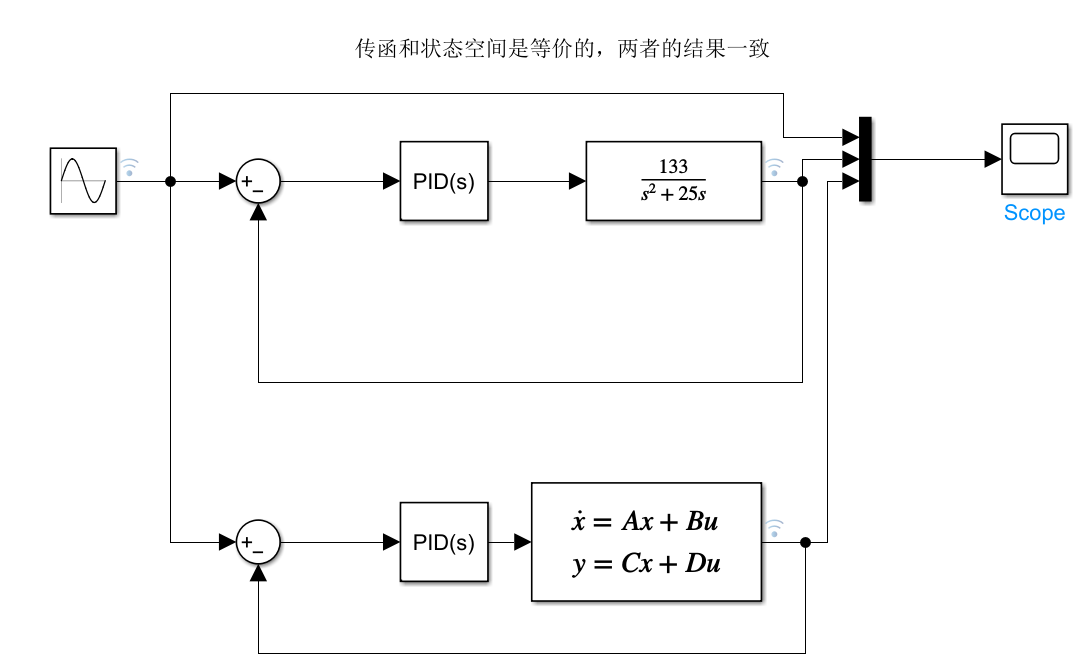
1.2 系统描述的两种形式–状态空间和传递函数 chap1_2.mdl

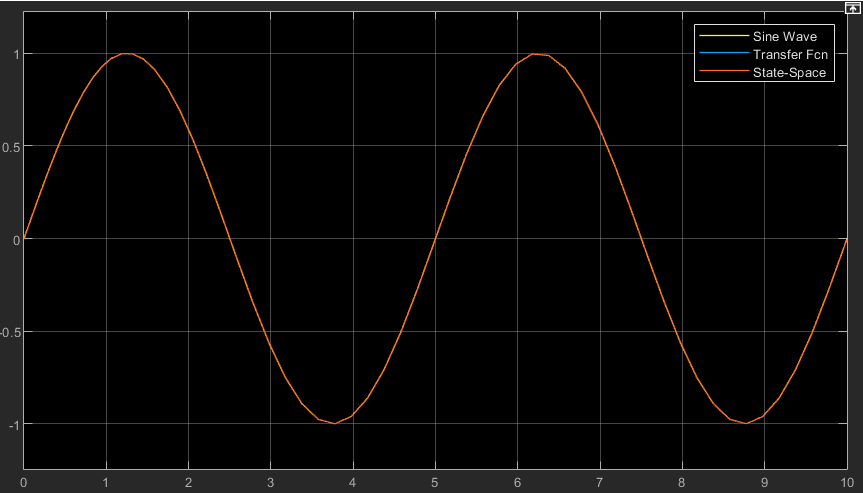
对比状态空间和传函两种形式的结果。连接两者的桥梁就是微分方程。

1.3 s-function 实现（连续系统） chap1_3.xls

前两个案例分别是通过传递函数和状态空间是实现系统模型，用的是matlab提供的现有控件。对于更加复杂的模型，我们可以通过s-function来实现。

所谓的s-function，就是一套固定的模板，matlab的求解器会按照这个固定的模板去调用你定义的函数。接下来，我们将先对s-function做一个简单介绍，在利用s-function分别实现PID控制器和被控系统。

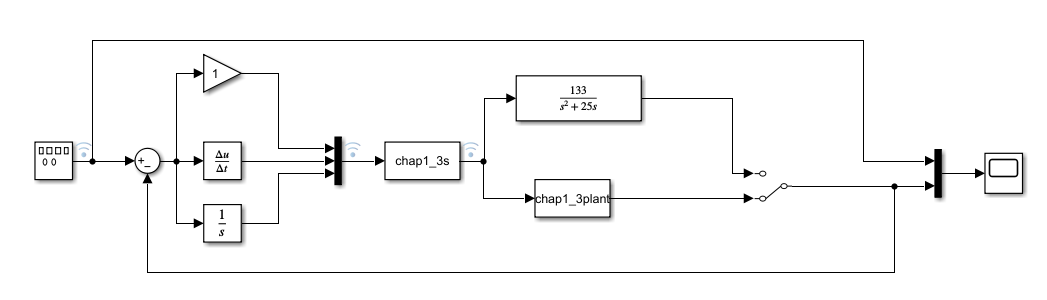
注意：不知道为什么，我在仿真的时候，发现两个系统模块不能并存，必须删除另一个才能正常。（就是switch没有起作用。后面有经验了再解决吧。）

（1）s-function

如下为一个s-function基本的结构：

[SYS,X0,STR,TS,SIMSTATECOMPLIANCE] = SFUNC(T,X,U,FLAG,P1,...,Pn)
switch flag,%%%%%%%%%%%%%%%%%%% Initialization %%%%%%%%%%%%%%%%%%%case 0,[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;%%%%%%%%%%%%%%%% Derivatives %%%%%%%%%%%%%%%%case 1,sys=mdlDerivatives(t,x,u);%%%%%%%%%%% Update %%%%%%%%%%%case 2,sys=mdlUpdate(t,x,u);%%%%%%%%%%%% Outputs %%%%%%%%%%%%case 3,sys=mdlOutputs(t,x,u);%%%%%%%%%%%%%%%%%%%%%%%% GetTimeOfNextVarHit %%%%%%%%%%%%%%%%%%%%%%%%case 4,sys=mdlGetTimeOfNextVarHit(t,x,u);%%%%%%%%%%%%%% Terminate %%%%%%%%%%%%%%case 9,sys=mdlTerminate(t,x,u);%%%%%%%%%%%%%%%%%%%%% Unexpected flags %%%%%%%%%%%%%%%%%%%%%otherwiseDAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));end

SFUNC某一时刻T的输出，取决于FLAG，当前状态向量X和当前的输入向量U。

不通过的FLAG，执行的结果如下所示：

%   FLAG   RESULT             DESCRIPTION
%   -----  ------             --------------------------------------------
%   0      [SIZES,X0,STR,TS]  Initialization, return system sizes in SYS,
%                             initial state in X0, state ordering strings
%                             in STR, and sample times in TS.
%   1      DX                 Return continuous state derivatives in SYS.
%   2      DS                 Update discrete states SYS = X(n+1)
%   3      Y                  Return outputs in SYS.
%   4      TNEXT              Return next time hit for variable step sample
%                             time in SYS.
%   5                         Reserved for future (root finding).
%   9      []                 Termination, perform any cleanup SYS=[].

我们需要做的，就是实现每个FLAG case下，具体的功能函数。
（2）PID的s-function案例
对于PID，只需要实现初始化、和输出部分。

% chap1_3s.m PID实现
function [sys,x0,str,ts] = pid_controller_with_antiwindup(t,x,u,flag)
% 带积分限幅的PID控制器S-function
% 输入: u(1)=error, u(2)=derror, u(3)=errori
% 输出: 控制量utswitch flagcase 0[sys,x0,str,ts]=mdlInitializeSizes;case {2, 4, 9}sys=[];case 3sys=mdlOutputs(t,x,u);otherwiseDAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
endfunction [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 1;
sizes.NumInputs      = 3;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;sys = simsizes(sizes);
x0  = [];
str = [];
ts  = [];
function sys=mdlOutputs(t,x,u)
error = u(1);
derror = u(2);
errori = u(3);% PID参数
kp = 60;
kd = 3;
ki = 1;% 积分限幅参数
integral_max = 100;   % 积分上限
integral_min = -100;  % 积分下限% 应用积分限幅
errori_limited = min(max(errori, integral_min), integral_max);% 计算PID输出
ut = kp*error + kd*derror + ki*errori_limited;% 输出限幅（可选）
output_max = 200;
output_min = -200;
ut_limited = min(max(ut, output_min), output_max);sys(1) = ut_limited;

（3） SYSTEM案例

同样的，系统也可以直接用S-function实现。（其效果等同于传递函数或状态空间。只不过S-FUNCTION是matlab提供的一个更通用的接口）
注意看初始化部分的变量注释。

unction [sys,x0,str,ts] = chap1_3plant(t,x,u,flag)
% 连续系统S-function实现
% 用于Simulink中的连续系统建模switch flagcase 0[sys,x0,str,ts]=mdlInitializeSizes;case 1sys=mdlDerivatives(t,x,u);case 2sys=[];case 3sys=mdlOutputs(t,x,u);case 4sys=[];case 9sys=[];otherwiseDAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
endfunction [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;% 如果为连续系统，状态变量的数量/维度 注意，是列向量
sizes.NumDiscStates  = 0;% 如果为离散系统，状态变量的数量/维度 注意，是列向量
sizes.NumOutputs     = 1;% 输出变量的维度数
sizes.NumInputs      = 1;% 输入变量的维度数
sizes.DirFeedthrough = 0; % 直馈 就是控制量u是否加入输出 y=Cx+Du，即此处是否出现u（注意，不是D的值），取值为0或1
sizes.NumSampleTimes = 1; % 模块采样周期的个数sys = simsizes(sizes);
x0  = [0; 0];% 注意，这里是列向量
str = [];
% ts 是一个 m×2 的矩阵，其中 ‌m 等于 sizes.NumSampleTimes 的值‌
% ts 矩阵的每一行定义了一个采样时间，其格式为 [采样周期, 偏移量]
% ‌连续采样时间‌（CONTINUOUS_SAMPLE_TIME）：值为0.0，适用于连续系统
%‌ 继承采样时间‌（INHERITED_SAMPLE_TIME）：值为-1.0，从驱动模块继承采样率
‌% 固定最小步长偏移‌（FIXED_IN_MINOR_STEP_OFFSET）：值为1.0
‌% 可变采样时间‌（VARIABLE_SAMPLE_TIME）：值为-2.0
ts  = [0 0];function [sys]=mdlDerivatives(t,x,u)
% 状态导数计算，确保数值稳定性
sys = zeros(2,1);% 状态方程: dx1/dt = x2
sys(1) = x(2);% 使用有界随机扰动，避免数值不稳定
rand_factor1 = max(min(randn(1), 2.0), -2.0);  % 限制在[-2,2]范围内
rand_factor2 = max(min(randn(1), 2.0), -2.0);% 状态方程: dx2/dt = -(25+10*rand_factor1)*x2 + (133+30*rand_factor2)*u
sys(2) = -(25 + 10 * rand_factor1) * x(2) + (133 + 30 * rand_factor2) * u(1);% 确保导数结果为有限值
if ~all(isfinite(sys))sys = zeros(2,1);
endfunction sys=mdlOutputs(t,x,u)
% 输出方程: y = x1
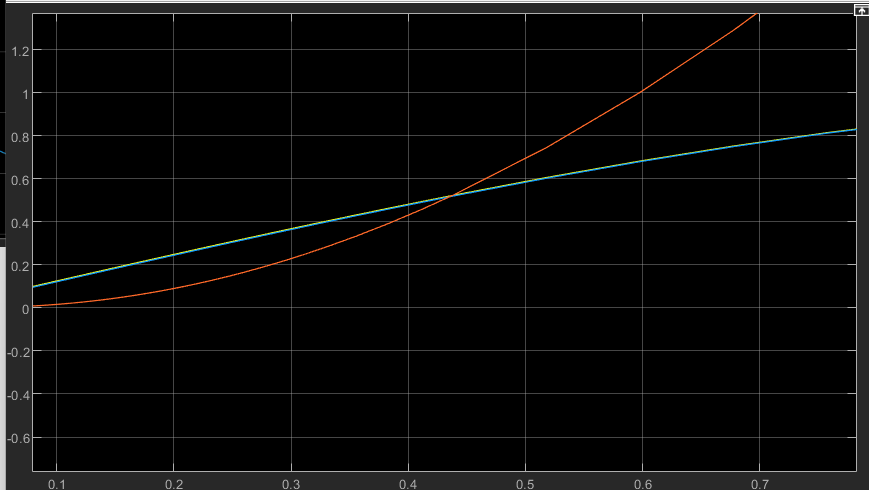
sys = x(1);

（4） 运行结果
两条曲线也基本重合。

1.4 s-function实现（离散系统）

对于离散系统和离散PID控制而言，离散化是实现系统的第一步。
一般而言，我们用物理规律写出的系统方程（微分方程的 状态空间形式或传递函数形式），都是针对连续系统的描述。但在控制领域中，更多的是以“步(长)”为单位对系统进行控制。因此，对连续系统的离散化十分必要。

s-function的实现后续再补充吧。

1.4.1 系统离散化方法

• 传递函数的离散形式：
  s变换->z变换。
  这部分方法很多，这里就举一个 双线性变换 的方法：
  $$s=\frac{2}{T}\frac{z-1}{z+1}$$
  用上述公式替代s方程中的s，然后执行Z变换。

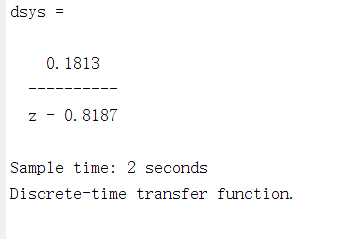
案例：在matlab中，可通过调用如下函数实现：

ts = 2;% 采样时间
sys = tf(1,[10,1]) % 连续系统
dsys = c2d(sys, ts, 'z') % 离散化 'z'/'zoh'：零阶保持器方法，这是默认选项
[num1, den1] = tfdata(dsys,'v') % 离散化后的零点和极点参数 'v'表示以向量的形式返回参数

输出如下：

• 状态空间的离散形式
  因为有状态变量导数项的存在，可直接用 差分近似导数的方法实现。（即欧拉法。）
  除此之外，还有向后欧拉、向前欧拉、梯形法等多种近似方法。
  同样的，也可以用双线性变换实现。

案例：
$$\dot{x}=Ax+Bu$$
$$x[k+1]=Gx[k]+Hu[k]$$

% 定义连续系统矩阵
A = [0 1; 1 -2];
B = [0; 1];
% 设置采样周期
Ts = 0.01;
% 使用c2d函数进行离散化
[G, H] = c2d(A, B, Ts);