【MATLAB例程】二维环境定位，GDOP和CRLB的计算，锚点数=4的情况（附代码下载链接）

本代码实现了在二维空间中使用四个锚点进行单目标定位的GDOP（几何定位精度）和CRLB（克拉美罗下界）计算。通过网格扫描法，计算不同位置的GDOP，并以等值线图的形式进行可视化。同时，代码还计算了目标真实位置的理论CRLB，从而评估定位精度。该方法为定位系统的性能评估提供了重要的理论依据。

以下是一个基于MATLAB的二维定位GDOP和CRLB计算示例，适用于单目标和四锚点场景。代码结合TDOA定位原理，包含GDOP等值线可视化：

% 二维定位GDOP与CRLB计算（单目标，四锚点）
% 2025-03-09/Ver1%% 参数设置
clear; clc; close all;
rng(0); % 固定随机种子% 锚点配置（正方形布局）
anchorPos = [0, 0;    % 锚点1100, 0;   % 锚点2100, 100; % 锚点30, 100];  % 锚点4 (单位：米)% 目标真实位置
truePos = [60, 40];   % 测试目标位置% 测量误差参数

运行结果：


代码下载链接：
https://download.csdn.net/download/callmeup/92201448

关键说明：

1. GDOP计算原理

   • 通过网格扫描生成测试点网格（-50m到150m）
   • 构建几何矩阵H，计算费舍尔信息矩阵(FIM)的逆矩阵
   • GDOP定义为协方差矩阵迹的平方根：$GDOP=\sqrt{tr(CRLB)}$

2. CRLB理论计算

   • 基于真实目标位置计算雅可比矩阵
   • 使用克拉美-罗下界公式：$CRLB=FI{M}^{-1}$

3. 可视化功能

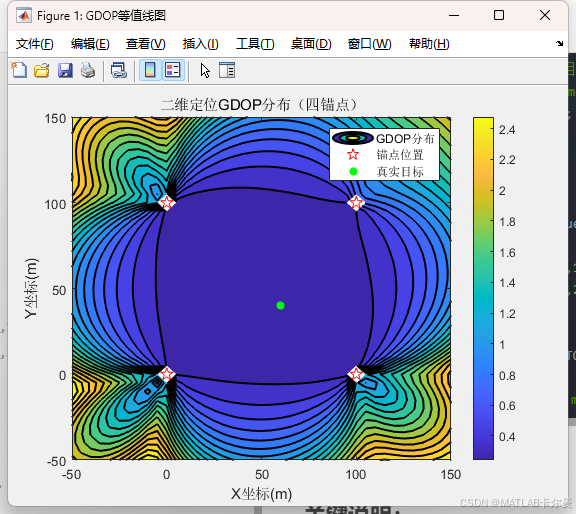
   • 生成GDOP等值线图，直观显示不同区域定位精度
   • 红色三角形标注锚点位置，绿色星号表示目标真实位置

运行结果说明

1. GDOP分布图显示锚点布局对精度的影响，最小GDOP通常出现在锚点包围区域中心
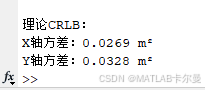
2. CRLB输出给出理论最小位置方差，可作为算法性能评估基准

更多定位相关代码，见专栏文章：
https://blog.csdn.net/callmeup/category_12794805.html

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者