hot 100（5） —— 盛最多水的容器（双指针）

一、设置left和right双指针遍历（最多面积由较小高度决定）+ 贪心思想

class Solution {public int maxArea(int[] height) {if(height == null || height.length == 0){return 0;}int left = 0;int right = height.length - 1;int maxArea = 0;while(left < right){int minHeight = Math.min(height[left],height[right]);int area = minHeight * (right - left);maxArea = Math.max(maxArea,area);while(left < right && height[left] <= minHeight){left++;}while(left < right && height[right] <= minHeight){right--;}}return maxArea;}
}

代码功能解释

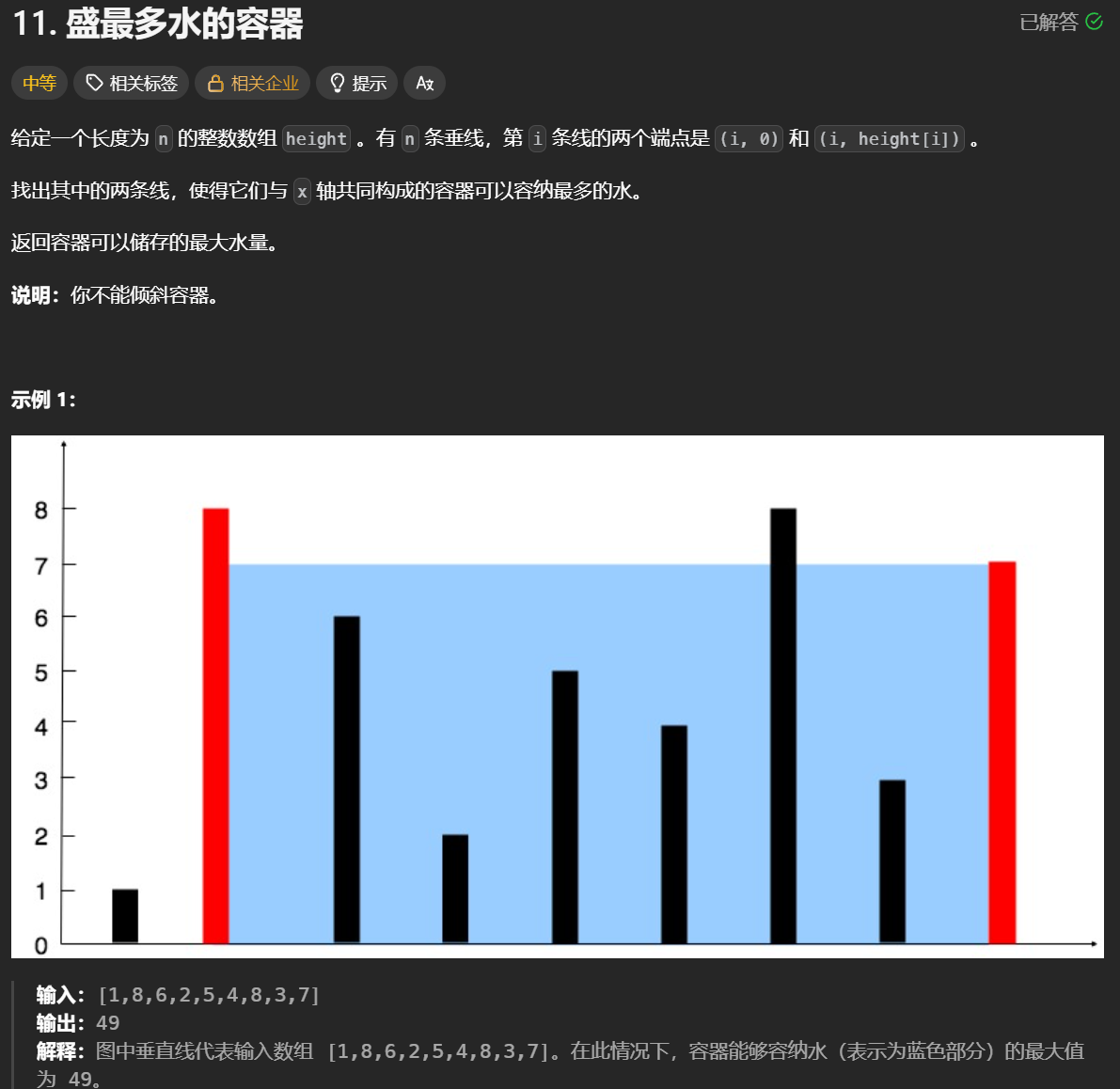
该代码用于求解盛最多水的容器问题：给定一个整数数组 height，其中每个元素代表坐标系中垂直于x轴的线段高度，找出两条线段与x轴组成的容器能容纳的最大水量。

核心逻辑基于“双指针法”，利用“贪心思想”优化：

1. 初始化指针：左指针 left 指向数组起始（0），右指针 right 指向数组末尾（height.length - 1），maxArea 记录最大水量（初始为0）。

2. 计算当前水量：容器水量由“短板高度”和“两板距离”决定，即 min(height[left], height[right]) * (right - left)，并更新 maxArea。

3. 移动短板指针：为了寻找更大水量，需移动较短的线段指针（若移动长板，两板距离减小且短板不变，水量必然减少），直到左右指针相遇。

时间复杂度

• O(n)，其中 n 是数组 height 的长度。

• 左右指针从数组两端向中间移动，每个元素最多被访问1次，仅需1轮遍历即可完成计算，无嵌套循环。

空间复杂度

• O(1)，即常数级空间。

• 仅使用 left、right、maxArea、minHeight 4个额外变量，空间消耗不随数组长度变化，属于原地算法。