机器学习日报03

摘要

通过学习神经网络的基础知识，我明白了激活函数的重要作用，并了解了如何处理多类别分类问题。本文主要分享了关于激活函数必要性、多类别分类概念以及Softmax回归原理的学习心得。

Abstract

Today I explore the importance of activation functions in neural networks and how to solve multi-class classification problems using Softmax regression. It first analyzes the problem of neural networks degenerating into linear models without activation functions, then introduces the concept of multi-class classification, and finally explains the principles of Softmax regression and its implementation in neural networks.

一、为什么我们需要激活函数

让我们来看看为什么神经网络需要激活函数，以及如果我们使用它们时为什么它们不起作用

回想一下这个需求预测示例，如果我们在这个神经网络的所有节点都使用线性激活函数会发生什么

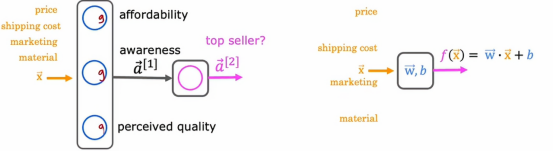
事实证明，这个大型网络将与线性回归没有任何区别

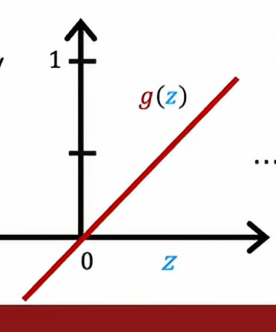
这样的话，该函数只能拟合线性回归模型，如果想之前我们学习的复杂模型，是完全不能的，这样没有达到神经网络的使用目的

让我们用一个更简单的例子来说明这点

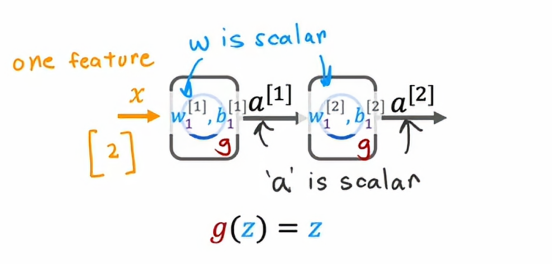
输入x是一个数字并且我们有一个隐藏单元参数w1和b1输出a1，这里只是一个数字，然后第二层是输出层，它只有一个输出单元，具有参数w2和b2以及输出a2，这也是一个数值、一个标量，即神经网络f(x)的输出

让我们看看如果在整个神经网络中使用线性激活函数会发生什么，为了计算a1，神经网络会使用a1 = w1·x + b1，然后a2 = w2·a1 + b2，我们把a1 = w1·x + b1 代入到后式中去，那么我们会得到

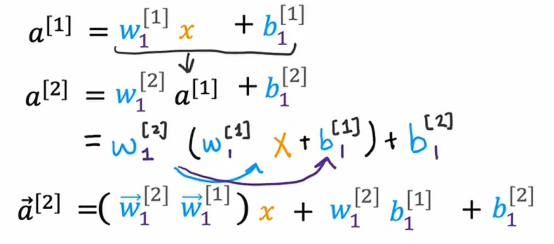
这样的话a2的表达式在形式上还是属于wx+b的情况，这无法体现我们运用了神经网络，因为我们看不出来这个是使用了一个隐藏层和一个输出层，这就与使用线性回归没有区别，甚至还不如使用了线性回归的模型，这就是为什么在神经网络中有多个层有时并不会让神经网络计算出任何更复杂的特征

总而言之，如果没有激活函数，无论神经网络有多少层，它都等价于一个单层的线性模型，这就完全丧失了神经网络强大的非线性表达能力，无法学习和模拟现实生活中的复杂非线性关系

二、多类

多类别分类指的是可能具有多个输出类别的分类问题，所以跟我们之前讨论的二元分类问题有一点小小区别，就是输出不仅仅是0和1了

对于我们目前所学习的手写数字分类问题，我们只是试图区分手写数字0和1，但如果我们需要尝试读取信封上的邮政编码，实际上我们需要识别的数字就有10个

或者换句话说，在我们刚开始接触这门课的时候说过一个例子，如果我们试图分类患者是否有任何三种或五种不同可能的疾病，亦或者如果我们在一座工厂里干活，我们可能会对生产的零件进行外观缺陷检测，我们会参考零件的预制图，试图判断它是否有刮痕缺陷、变色缺陷或缺角缺陷，这些都属于是多类问题，实际上多类别分类问题仍然是一个分类问题，因为y只能取一些少量的值，这不是任意数量，但现在y可以取超过2个可能的值

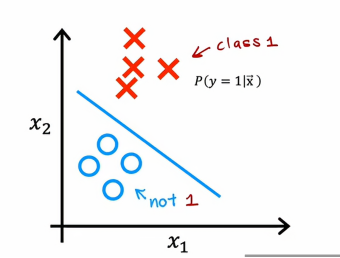
上图是之前提到的二元分类的数据集，包含特征x1和x2，在这种情况下，逻辑回归会拟合一个模型来估计给定特征x时y为1的概率

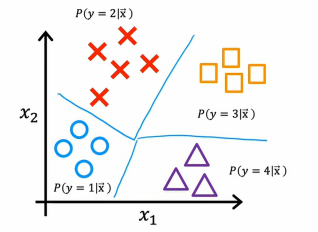
多类问题的数据集如上图所示，一个形状代表一个类别，现在我们不仅仅要估计y = 1的概率，还要估计y =2，y=3，y=4的概率

所以这是多类别分类问题的定义，在一个小节中，我们将学习softmax回归算法，使用它，我们将能够处理多类别分类问题，之后还能将softmax回归和新的神经网络结合起来，这样我们可以训练一个神经网络来处理多类别分类问题

三、softmax

Softmax回归算法是对逻辑回归的一种扩展，逻辑回归是一种二分类算法，而softmax则是在逻辑回归的扩展下形成的，让我们来看看它们是如何工作的

1、回顾逻辑回归

我们先来简单回顾一下逻辑回归，逻辑回归适用于y可以有两个可能的输出值，它计算输出的方式是，我们首先计算z = w·x + b ，然后我们再计算a =g（z）= 1/1+e-z，这里的g被称为是sigmoid函数，我们将其解释为逻辑回归在给定输入时y = 1的概率

2、推广到softmax

为了推广到softmax回归，我们将把逻辑回归看作实际上计算两个数，首先是a1，即我们之前谈到的y在给定x时等于1的概率，其次，我们将把逻辑回归看作也计算a2，也就是y在给定输入特征x时等于0的概率，当然a1+a2 = 1

现在我们推广到y有四个不同输出的情况，即y=1，2，3，4，我们将计算y输出的不同情况

由上面图我们可以看出，z1、z2、z3、z4这些都是softmax回归的参数，右边则是softmax回归的公式，a1、a2、a3、a4将被解释为算法估计的y = 1、2、3、4的概率，同逻辑回归，a1 + a2 + a3 +a4 = 1

3、softmax公式的广义表达

Softmax公式推导如下：

3.1、指定代价函数

从上图曲线可以看出，当aj越大，损失就小，当aj越小，损失就越大，所以我们的算法需要将aj尽可能的增大

总结

通过学习这部分内容，我深刻认识到激活函数是神经网络能够解决复杂问题的关键。同时，Softmax回归为我们处理多类别分类问题提供了有效的方法。这些知识让我对神经网络的应用有了更全面的理解，也为后续学习打下了坚实基础。