当前位置：首页 > news >正文

使用Mathematica编写一个高效的Langevin方程求解器

news 2025/10/25 8:10:43

考察关于随机变量X，简单的Langevin随机微分方程：

其中f(X)是任意给定的函数以及ζ(t)是一个高斯型白噪声，满足

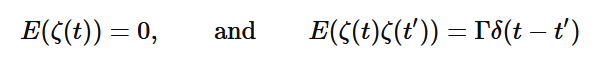
使用Euler-Maruyama方法求解：将时间离散化t=ndt并使用迭代

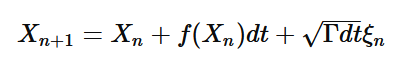
其中ξ_n∼N(0,1). 将这个迭代格式编写成Mathematica代码

Langevin[x0_, f_, G_, tf_, n_, m_ : 1] := With[{dt = N[tf/n], s = N[Sqrt[tf G/n]], xx0 = Table[x0, {m}]}, Transpose@NestList[# + dt f[#] + RandomVariate[NormalDistribution[0, s], m] &, xx0, n]];

其中：（1）x0是初始条件；（2）函数f(x)；（3）谱密度Γ =G；（4）终点时间t_f 和（5）离散区间数n。相应的，离散区间长度为dt=t_f/n. 输出为一个（m+1）向量：

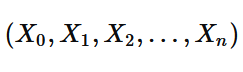
双稳态位势

下面给出一个示例，关于双稳态位势

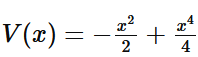
相应地

其模拟了冷热连个条件，分别对应于：data1 中的Γ=0.1 和 data2 中的Γ=1.

data1 = Langevin[0, -#^3 + # &, 0.1, 10, 10^3, 2000];
data2 = Langevin[0, -#^3 + # &, 1, 10, 10^3, 2000];

为了分析系统的稳态结构，我们丢掉前面8成的点，来观察剩下的点的分布状态。尤其是要观察其在位势极小值点附近的分布以及冷热条件对于分布的影响：

Show[Histogram[{Flatten[data1[[All, 800 ;; 1000]]], Flatten[data2[[All, 800 ;; 1000]]]},Automatic, "PDF"],Plot[-z^2/2 + z^4/4, {z, -1.8, 1.8},PlotStyle -> Red], AxesOrigin -> {0, 0},PlotRange -> {-0.3, 1.2}]