加性高斯白噪声和码间串扰的信道中Ungerboeck和Forney接收机的区别

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

在序列检测领域，Ungerboeck 与 Forney 两种离散观测模型可视为同一最大似然判决的两种等效表达。它们在信道与噪声统计已知且实现无失真的理想条件下性能等价，关键差别体现在白化的位置与度量的形式。Forney 接收机在执行匹配滤波后，加性高斯白噪声（AWGN）有色化，需要采用白化匹配滤波进行白化操作，之后使得 Viterbi 或 BCJR 算法可直接使用欧几里得度量作为度量值。其状态数大致等于因果码间串扰（ISI）记忆，具体实现简洁高效，但在窄带条件下可能引入噪声增强。Ungerboeck 接收机保留匹配滤波后的有色噪声，在分支度量中显式纳入噪声协方差，常借助预测或创新滤波完成“度量白化”，有效记忆等于信道记忆与预测阶数之和，复杂度更高但对部分响应与严重带宽限制场景更稳健。

---

一、AWGN+ISI信道模型

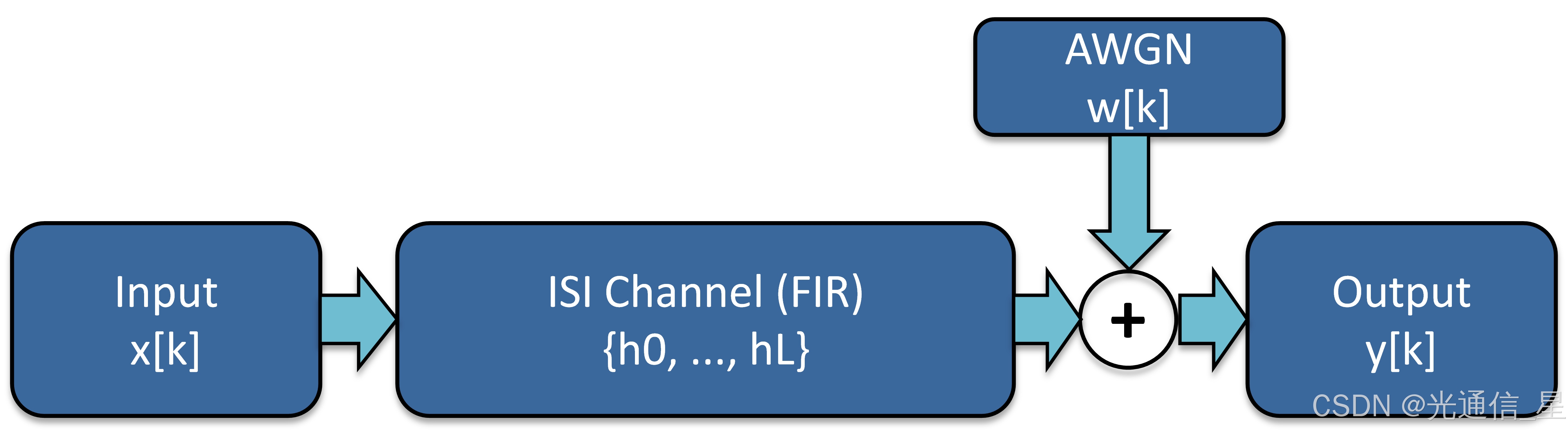
图1 等效的离散时间AWGN+ISI信道模型
图1展示的是等效离散时间 ISI 信道：离散输入序列 $x[k]$ 经过有限冲激响应（FIR）通道h={h0,…,hL}h=\{h_0,\ldots,h_L\}h={h0​,…,hL​} 后，在求和节点与加性白高斯噪声（AWGN）$w[k]$ 相加，得到输出 $y[k]$。其数学形式为
公式(1): $y[k]={\sum }_{\ell =0}^L{h}_{\ell }x[k-\ell ]+w[k].$
其中 $h$ 表示由脉冲成形、信道与接收滤波共同导致的ISI，$L$ 为记忆长度。

二、接收机模型及原理

图2 Forney和Ungerboeck接收机模型

1.Forney接收机

首先对 $y(t)$ 用常规匹配滤波器 $h^{\ast }(-t)$ 并在符号时刻取样，得到
公式(2): $z_k\triangleq {\int }_{-\infty }^{\infty }y(t)h^{\ast }(t-kT)dt={\sum }_{\ell }{g}_{\ell }{a}_{k-\ell }+v_k,$
其中 $g_{\ell }\triangleq {\int }_{-\infty }^{\infty }h(t)h^{\ast }(t-\ell T)dt$ 为自相关抽头，噪声为有色高斯过程
公式(3): E{vkvm∗}=N0gk−m.\mathbb{E}\{v_k v_m^*\} = N_0\,g_{k-m}.E{vk​vm∗​}=N0​gk−m​.

定义 $G(z)\triangleq {\sum }_{\ell =-\infty }^{\infty }{g}_{\ell }{z}^{-\ell }$，做谱因子分解（最小相位、monic）
公式(4): $G(z)={\sigma }_w^{2}F(z)F^{\ast }(1/z^{\ast }),$
其中 $F(z)={\sum }_{\ell =0}^L{f}_{\ell }{z}^{-\ell }$ 为因果最小相位多项式，${\sigma }_w^2$ 为白化后噪声方差。
取白化匹配滤波器（WMF）
公式(5): $W(z)\triangleq \frac{1}{F^{\ast }(1/z^{\ast })},$
将其作用到 {zk}\{z_k\}{zk​} 上得到白噪声观测
公式(6): yk=(W∗z)k=∑ℓ=0Lfℓak−ℓ+wk,E{wkwm∗}=σw2δ[k−m].y_k = (W*z)_k = \sum_{\ell=0}^{L} f_\ell\,a_{k-\ell} + w_k,\quad \mathbb{E}\{w_k w_m^*\}=\sigma_w^{2}\delta[k-m].yk​=(W∗z)k​=∑ℓ=0L​fℓ​ak−ℓ​+wk​,E{wk​wm∗​}=σw2​δ[k−m].

在此白化模型下，观测似然可按独立样本分解，与前述“公式(2)”一致，可写为
公式(7): $p(\mathbf{y}\mid \mathbf{a})={\prod }_{k}p(y_k\mid \mathbf{a}),p(y_k\mid \mathbf{a})\propto \exp \{-\frac{1}{2{\sigma }_w^2}|y_k-{\sum }_{\ell =0}^L{f}_{\ell }{a}_{k-\ell }{|}^2\}.$

由此得到基于分支度量的 MAP/MLSE 实现（与“公式(3)”一致）：
公式(8): ${\lambda }_k(a_k,{\sigma }_k)=|y_k-{\sum }_{\ell =0}^L{f}_{\ell }{a}_{k-\ell }{|}^2+2{\sigma }_w^2\ln P(a_k\mid {\sigma }_k),$
先验均匀时退化为欧几里得度量的 MLSE。

2.Ungerboeck接收机

Ungerboeck 采用常规匹配滤波器$h^{\ast }(-t)$ 并在符号时刻取样，得到充分统计量
公式(9): $z_k\triangleq {\int }_{-\infty }^{\infty }y(t)h^{\ast }(t-kT)dt$。
定义通道自相关抽头
公式(10): $g_{\ell }\triangleq {\int }_{-\infty }^{\infty }h(t)h^{\ast }(t-\ell T)dt$，
则 {zk}\{z_k\}{zk​} 满足
公式(11): $z_k={\sum }_{\ell }{g}_{\ell }{a}_{k-\ell }+n_k$，
噪声 {nk}\{n_k\}{nk​} 为零均值复高斯过程，协方差
公式(12): E{nknm∗}=N0gk−m\mathbb{E}\{n_k n_m^*\}=N_0\,g_{k-m}E{nk​nm∗​}=N0​gk−m​（有色）。

对数似然的负号（等价度量）可写成连续时间能量形式
公式(13): $J_U(\mathbf{a})\triangleq {\int }_{-\infty }^{\infty }{\left|y(t)-{\sum }_n{a}_{n}h(t-nT)\right|}^{2}dt$。
将其按“常数项 + 相关项 + 自相关项”展开，有
公式(14): $J_U(\mathbf{a})=A-2\Re {\sum }_n{a}_n^{\ast }{z}_n+{\sum }_k{\sum }_n{a}_k{a}_n^{\ast }{g}_{n-k}$，
其中 $A=\int |y(t){|}^{2}dt$ 与序列 $\mathbf{a}$ 无关，可在判决中忽略。

因此，基于 Ungerboeck 充分统计量的 ML/MAP 序列检测可在与信道记忆相同的网格上实现。令状态 ${\sigma }_k=(a_{k-1},\dots ,a_{k-L})$，则分支度量可取为
公式(15): $B{M}_k(a_k,{\sigma }_k)=g_0|a_k{|}^2-2\Re \{a_k^{\ast }(z_k-{\sum }_{\ell =1}^L{g}_{\ell }{a}_{k-\ell })\}$（MAP 时再加上先验项 $+2N_0\ln P(a_k\mid {\sigma }_k)$）。

总结

在 Forney 接收机中，MLSE 的分支度量通常采用欧几里得距离；该做法在噪声为白噪声时最为简洁高效。实际流程是先经常规模型的匹配滤波得到含有色噪声的观测$z_k={\sum }_{\ell }{g}_{\ell }{a}_{k-\ell }+v_k$，其中噪声协方差为E{vkvm∗}=N0gk−m\mathbb{E}\{v_k v_m^{*}\}=N_0\,g_{k-m}E{vk​vm∗​}=N0​gk−m​。随后对自相关谱因子分解并施加 WMF进行白化，得到$y_k={\sum }_{\ell =0}^L{f}_{\ell }{a}_{k-\ell }+w_k$，且 E{wkwm∗}=σw2δ[k−m]\mathbb{E}\{w_k w_m^{*}\}=\sigma_w^{2}\delta[k-m]E{wk​wm∗​}=σw2​δ[k−m]。此时即可用欧几里得度量实现 MLSE/Viterbi/BCJR；若保持有色噪声而不白化，则应改用似然概率度量（在分支度量中显式包含噪声协方差）。与之相对，Ungerboeck 接收机保留匹配滤波输出的有色噪声模型，在分支度量中通过创新/预测滤波完成“度量内白化”，无需显式 WMF。在信道与噪声统计已知时，两者在性能上等价。