非视距城市合成孔径雷达中的多径利用——论文阅读
非视距城市合成孔径雷达中的多径利用。
摘要与引言:在遮挡中“看见”
在雷达应用中,尤其是密集的城市环境,建筑物等障碍物造成的遮挡是一个核心难题。当目标位于雷达的直接视距 (Line of Sight, LOS) 之外时,传统雷达系统将无法探测到它。然而,城市环境也是一个充满电磁反射的环境。信号会经由建筑墙面等表面反射,产生多条(即“多径”)从雷达传播到目标再返回的路径。对于传统的合成孔径雷达 (Synthetic Aperture Radar, SAR) 波束形成算法而言,这些多径返回信号是“虚假”的,它们不仅无法在目标的真实位置正确成像,还会在雷达图像上的其他位置产生“鬼影”或虚警 (False Alarms)。
本文的核心思想是变废为宝:它不再将多径视为干扰,而是将其作为一种可利用的信号资源。文章提出了两种新的信号处理技术,专门用于利用这些多径返回信号,在目标完全没有LOS路径的情况下,反演出其真实的、被遮挡的位置。
实现这一目标的前提假设是:
- 环境几何已知:雷达“知道”反射墙面的位置和几何形状(例如,通过市政蓝图或先前的UAV侦察获得)。
- 多径可解析:多径信号是可探测且可分辨的。
- 主要考虑镜面反射:假设多径可以被视为镜面反射(Specular Reflection),而衍射(Diffraction)等更复杂的效应可以被忽略。
本文提出的两种技术分别在数据域(直接处理原始雷达回波)和图像域(处理已生成的传统SAR图像)上运行。它们的目标都是将那些由多径产生的“虚警”关联起来,并将它们“映射”回目标真实的阴影位置,从而在消除虚警的同时,显著提高目标真实位置的信噪比 (Signal to Clutter Ratio, SCR)。
文章通过两种典型的城市场景来检验这些技术:城市峡谷(目标隐藏在小巷中)和 T形交叉口(目标隐藏在拐角后)。
自由空间成像基础:传统SAR的数学模型
为了理解新技术的创新之处,我们首先需要回顾传统SAR(自由空间,即假设没有多径)的成像原理。
假设一个点目标位于 xt=[xt,yt]Tx_{t}=[x_{t},y_{t}]^{T}xt=[xt,yt]T,雷达传感器在 MMM 个不同位置 rmr_{m}rm ( m=1,2,…,Mm=1, 2, \dots, Mm=1,2,…,M ) 进行观测。在第 mmm 个位置,雷达发射波形 sm(t)s_{m}(t)sm(t):
sm(t)=p(t−(m−1)Tp)exp(jωc(t−(m−1)Tp))s_{m}(t)=p(t-(m-1)T_{p})exp(j\omega_{c}(t-(m-1)T_{p}))sm(t)=p(t−(m−1)Tp)exp(jωc(t−(m−1)Tp))
其中 p(t)p(t)p(t) 是基带波形,ωc\omega_{c}ωc 是载波频率。
接收到的回波信号 rm(t)r_{m}(t)rm(t) 是发射信号的延迟和衰减版本,并混有噪声 vm(t)v_{m}(t)vm(t):
rm(t)=ρmsm(t−2τ(xt;rm))+vm(t)r_{m}(t)=\rho_{m}s_{m}(t-2\tau(x_{t};r_{m}))+v_{m}(t)rm(t)=ρmsm(t−2τ(xt;rm))+vm(t)
这里的 ρm\rho_{m}ρm 是目标的雷达截面 (RCS),τ(a;b)=∣∣a−b∣∣/c\tau(a;b)=||a-b||/cτ(a;b)=∣∣a−b∣∣/c 是信号在 aaa 和 bbb 之间的单程传播时延, ccc 是光速。
传统SAR成像(例如,通过反向投影算法)的核心是波束形成。它试图在图像网格的每一个“像素” xxx 上重建信号强度。其计算公式 Io(x)\mathcal{I}_{o}(x)Io(x) 如下:
Io(x)=∑m=1M{rm(t+2τ(x;rm))⊕sm∗(−t)}∣t=0\mathcal{I}_{o}(x)=\sum_{m=1}^{M}\{r_{m}(t+2\tau(x;r_{m}))\oplus s_{m}^{*}(-t)\}|_{t=0}Io(x)=m=1∑M{rm(t+2τ(x;rm))⊕sm∗(−t)}∣t=0
这个公式 (3) 的含义是:
- 时间对齐:对于一个假设的像素点 xxx,计算信号从 rmr_mrm 到 xxx 再返回的往返时延 2τ(x;rm)2\tau(x;r_m)2τ(x;rm)。将接收到的信号 rm(t)r_m(t)rm(t) 按照这个时延进行“反向”时移,得到 rm(t+2τ(x;rm))r_{m}(t+2\tau(x;r_{m}))rm(t+2τ(x;rm))。
- 匹配滤波:将时移后的信号与发射信号的复共轭时间反褶 sm∗(−t)s_{m}^{*}(-t)sm∗(−t) 进行卷积 ( ⊕\oplus⊕ )。这本质上是一个匹配滤波操作,用于压缩脉冲,最大化信噪比。
- 相干累加:在 t=0t=0t=0 时刻对匹配滤波的输出进行采样,并将所有 MMM 个传感器位置上的采样值相干地叠加起来。
如果假设的位置 xxx 恰好等于目标的真实位置 xtx_txt,那么来自所有 MMM 个传感器的信号都会同相叠加,在 Io(xt)\mathcal{I}_{o}(x_t)Io(xt) 处形成一个强烈的峰值。如果 x≠xtx \ne x_tx=xt,信号会失相,叠加后相互抵消。
多径模型:虚假目标的产生
现在,我们进入本文的核心问题:非视距 (NLOS) 场景。
场景一:城市峡谷 (Urban Canyon)
如下图1所示,传感器 rmr_mrm 位于巷口,目标 xtx_txt 隐藏在巷内深处,并被一个障碍物遮挡,导致没有LOS路径。但是,信号可以通过墙1、墙2和墙3反射到达目标。
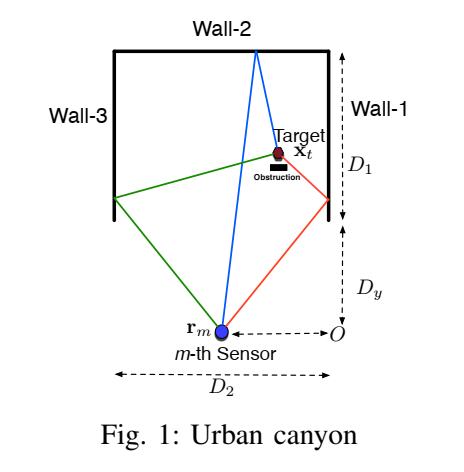
根据几何光学,每一次镜面反射都等效于一个“虚拟目标” (Virtual Target)。例如,经由墙1的反射,看起来就像是信号来自位于墙1另一侧等距的虚拟目标 x1vtx_{1}^{vt}x1vt。这三个虚拟目标的位置 χkvt\chi_{k}^{vt}χkvt (这里用 xkvtx_{k}^{vt}xkvt 表示) 计算如下:
x1vt:=[xt,yt]Tx_{1}^{vt}:=[x_{t},y_{t}]^{T}x1vt:=[xt,yt]T
x2vt:=[−xt,2(D1+Dy)−yt)]Tx_{2}^{vt}:=[-x_{t},2(D_{1}+D_{y})-y_{t})]^{T}x2vt:=[−xt,2(D1+Dy)−yt)]T
x3vt:=[−(2D2−xt),yt]Tx_{3}^{vt}:=[-(2D_{2}-x_{t}),y_{t}]^{T}x3vt:=[−(2D2−xt),yt]T
在这种情况下,雷达接收到的信号 rm(t)r_m(t)rm(t) 不再包含来自 xtx_txt 的直接回波,而是变成了纯粹的多径回波的叠加:
rm(t)=∑k=13ρmksm(t−2τ(xkvt;rm))+vm(t)r_{m}(t)=\sum_{k=1}^{3}\rho_{mk}s_{m}(t-2\tau(x_{k}^{vt};r_{m}))+v_{m}(t)rm(t)=k=1∑3ρmksm(t−2τ(xkvt;rm))+vm(t)
这是本文的核心信号模型 (公式 5)。如果我们把这个信号 rm(t)r_m(t)rm(t) 代入传统的SAR成像公式 (3),会发生什么?
传统算法并不知道这些是多径。它会像处理正常信号一样,在 x=x1vtx = x_{1}^{vt}x=x1vt, x=x2vtx = x_{2}^{vt}x=x2vt 和 x=x3vtx = x_{3}^{vt}x=x3vt 的位置上形成三个强烈的峰值。算法会“错误地”报告在这些虚拟位置上有三个目标,而目标的真实位置 xtx_txt 处则是一片空白。
场景二:T形交叉口 (T-junction)
如下图2所示,目标 xtx_txt 隐藏在拐角后,被墙3遮挡。同样,信号可以通过墙1、墙2以及墙3和墙2的组合反射到达目标。
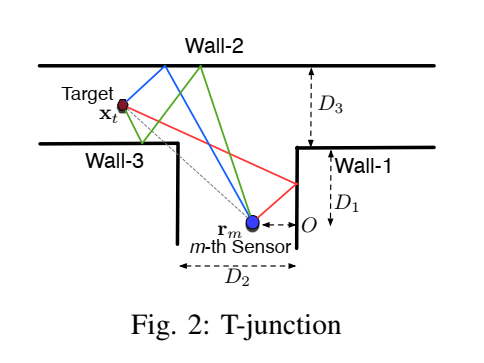
这同样会产生三个虚拟目标 χkvt\chi_{k}^{vt}χkvt (这里用 ykvty_{k}^{vt}ykvt 表示):
y1vt=[xt,yt]Ty_{1}^{vt}=[x_{t},y_{t}]^{T}y1vt=[xt,yt]T
y2vt=[−xt,2(D3+D1)−yt]Ty_{2}^{vt}=[-x_{t},2(D_{3}+D_{1})-y_{t}]^{T}y2vt=[−xt,2(D3+D1)−yt]T
y3vt=[−xt,2D3+,yt]Ty_{3}^{vt}=[-x_{t},2D_{3}+,y_{t}]^{T}y3vt=[−xt,2D3+,yt]T
同样,传统SAR处理会在这三个虚拟位置上产生虚警,而无法探测到 xtx_txt。此外,论文还通过公式 (7) 到 (10) 详细推导了目标必须满足的几何约束条件,例如,公式 (7) ⋂m=1M{(xt,yt):yt(dm−D2)dm−xt≤D1}\bigcap_{m=1}^{M}\{(x_{t},y_{t}):\frac{y_{t}(d_{m}-D_{2})}{d_{m}-x_{t}}\le D_{1}\}⋂m=1M{(xt,yt):dm−xtyt(dm−D2)≤D1} 定义了目标 xtx_txt 必须位于哪个区域内才能保证它始终被墙3遮挡,对所有传感器位置 rmr_mrm 都不可见。
多径利用技术 (Multipath Exploitation)
本文的目标是设计一种算法,该算法的输出是在 xtx_txt 处产生峰值,而在 xkvtx_{k}^{vt}xkvt 处不产生峰值。
A. 数据域 (Data Domain) 利用技术
该技术通过修改传统的波束形成公式 (3) 来实现。它不再对LOS路径进行反向投影,而是利用已知的墙体几何信息,在算法内部进行“多径反向投影”。
其核心思想是:
对于网格上每一个假设的目标位置 x∈Wsubx \in \mathcal{W}_{sub}x∈Wsub (其中 Wsub\mathcal{W}_{sub}Wsub 是目标可能存在的阴影区域),我们首先根据几何关系计算出它将会产生的 KKK 个(本文为3个)虚拟目标位置,记为 χ‾kvt\overline{\chi}_{k}^{vt}χkvt。
然后,我们使用这些假设的虚拟位置 χ‾kvt\overline{\chi}_{k}^{vt}χkvt 来对齐接收到的信号 rm(t)r_m(t)rm(t),并将所有 KKK 个多径的能量相干地累加到假设的真实位置 xxx 上。
修改后的波束形成图像 I1(x)\mathcal{I}_{1}(x)I1(x) 计算如下:
I1(x)=∑m=1M∑k=13{rm(t+2τ(χ‾kvt;rm))⊕sm∗(−t)}∣t=0\mathcal{I}_{1}(x)=\sum_{m=1}^{M}\sum_{k=1}^{3}\{r_{m}(t+2\tau(\overline{\chi}_{k}^{vt};r_{m}))\oplus s_{m}^{*}(-t)\}|_{t=0}I1(x)=m=1∑Mk=1∑3{rm(t+2τ(χkvt;rm))⊕sm∗(−t)}∣t=0
这是本文的第一个关键算法 (公式 11)。
工作原理:
- 当 x≠xtx \ne x_tx=xt 时:假设的虚拟位置 χ‾kvt\overline{\chi}_{k}^{vt}χkvt 与信号中 实际的 虚拟位置 χkvt\chi_{k}^{vt}χkvt (来自公式 5) 不匹配。时移 2τ(χ‾kvt;rm)2\tau(\overline{\chi}_{k}^{vt};r_{m})2τ(χkvt;rm) 是错误的,信号无法对齐,相干累加后相互抵消,I1(x)\mathcal{I}_{1}(x)I1(x) 很小。
- 当 x=xtx = x_tx=xt 时:假设的 xxx 恰好是真实目标位置。此时,我们计算出的假设虚拟位置 χ‾kvt\overline{\chi}_{k}^{vt}χkvt 将会精确地等于信号中实际的虚拟位置 χkvt\chi_{k}^{vt}χkvt。因此,公式 (11) 中的时移 2τ(χ‾kvt;rm)2\tau(\overline{\chi}_{k}^{vt};r_{m})2τ(χkvt;rm) 完美地对齐了公式 (5) 中 rm(t)r_m(t)rm(t) 包含的所有 KKK 个多径分量。这 KKK 个分量将同时同相地叠加,在 I1(xt)\mathcal{I}_{1}(x_t)I1(xt) 处产生一个非常强烈的峰值。
这种方法将传统算法认为是虚警的 KKK 个信号源,转变为了 KKK 个用于相干累加的“有效传感器”,极大地提高了 xtx_txt 处的能量。
复合点扩散函数 (CPSF)
为了分析这种新算法的成像质量,作者引入了复合点扩散函数 (CPSF) 的概念。
首先,传统LOS场景下的点扩散函数 (PSF) P(xt,x)\mathcal{P}(x_{t},x)P(xt,x) (公式 14) 描述了当真实目标在 xtx_txt 时,在 xxx 处成像的响应:
P(xt,x)=∑m=1MF−1{∣P(ω−ωc)∣2exp(−j(ω−ωc)2Δτm(xt;x))exp(−jωc2Δτm(xt;x))}∣t=0\mathcal{P}(x_{t},x)=\sum_{m=1}^{M}\mathcal{F}^{-1}\{|P(\omega-\omega_{c})|^{2} exp(-j(\omega-\omega_{c})2\Delta\tau_{m}(x_{t};x))exp(-j\omega_{c}2\Delta\tau_{m}(x_{t};x))\}|_{t=0}P(xt,x)=m=1∑MF−1{∣P(ω−ωc)∣2exp(−j(ω−ωc)2Δτm(xt;x))exp(−jωc2Δτm(xt;x))}∣t=0
其中 Δτm(xt;x):=τ(xt;rm)−τ(x;rm)\Delta\tau_{m}(x_{t};x):=\tau(x_{t};r_{m})-\tau(x;r_{m})Δτm(xt;x):=τ(xt;rm)−τ(x;rm)。
现在,将多径信号模型 (5) 代入新的数据域算法 (11),并假设 ρmk=1\rho_{mk}=1ρmk=1 且无噪声,我们得到CPSF Pc(xt,x)\mathcal{P}_{c}(x_{t},x)Pc(xt,x):
Pc(xt,x)=∑m=1M∑k=13∑l=13F−1{∣P(ω−ωc)∣2×exp(−j(ω−ωc)2Δτmkl(χkvt;χ‾lvt))×exp(−jωc2Δτmkl(χkvt;χ‾lvt))}∣t=0\mathcal{P}_{c}(x_{t},x)=\sum_{m=1}^{M}\sum_{k=1}^{3}\sum_{l=1}^{3}\mathcal{F}^{-1}\{|P(\omega-\omega_{c})|^{2} \times exp(-j(\omega-\omega_{c})2\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt})) \times exp(-j\omega_{c}2\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt}))\}|_{t=0}Pc(xt,x)=m=1∑Mk=1∑3l=1∑3F−1{∣P(ω−ωc)∣2×exp(−j(ω−ωc)2Δτmkl(χkvt;χlvt))×exp(−jωc2Δτmkl(χkvt;χlvt))}∣t=0
其中 Δτmkl(χkvt;χ‾lvt):=τ(χkvt;rm)−τ(χ‾lvt;rm)\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt}):=\tau(\chi_{k}^{vt};r_{m})-\tau(\overline{\chi}_{l}^{vt};r_{m})Δτmkl(χkvt;χlvt):=τ(χkvt;rm)−τ(χlvt;rm)。
这个CPSF可以被分解为两个部分:
- 期望项 Qc(xt,x)\mathcal{Q}_{c}(x_{t},x)Qc(xt,x) (当 k=lk=lk=l 时,公式 13):
Qc(xt,x)=∑m=1M∑k=13F−1{…exp(−jωc2Δτmkk(χkvt;χ‾kvt))… }∣t=0\mathcal{Q}_{c}(x_{t},x)=\sum_{m=1}^{M}\sum_{k=1}^{3}\mathcal{F}^{-1}\{\dots exp(-j\omega_{c}2\Delta\tau_{mkk}(\chi_{k}^{vt};\overline{\chi}_{k}^{vt}))\dots\}|_{t=0}Qc(xt,x)=m=1∑Mk=1∑3F−1{…exp(−jωc2Δτmkk(χkvt;χkvt))…}∣t=0
这是我们期望的成像结果,它本质上是 KKK 个多径分量各自的PSF的相干叠加。 - 干扰项 (当 k≠lk \ne lk=l 时):
这是由不同多径路径(例如,路径1的信号与路径2的假设时延)之间的“交叉”匹配滤波引起的,它在传统PSF中不存在。
B. 图像域 (Image Domain) 利用技术
该技术不修改波束形成过程,而是对传统SAR生成的、充满虚警的图像 IoI_oIo 进行后处理。
其核心思想是“掩膜与关联” (Mask and Associate):
- 生成虚警图像:首先,运行传统SAR算法 (公式 3),得到原始的波束形成图像 IoI_oIo。这张图像在 xtx_txt 处没有峰值,但在 KKK 个虚拟位置 χkvt\chi_{k}^{vt}χkvt 处有强烈的“虚警”峰值。
- 遍历假设:与数据域方法类似,我们遍历所有假设的目标位置 x~t∈Wsub\tilde{x}_{t} \in \mathcal{W}_{sub}x~t∈Wsub。
- 生成PSF掩膜:对于每一个 x~t\tilde{x}_{t}x~t,我们计算出它对应的 KKK 个虚拟位置 χ~kvt\tilde{\chi}_{k}^{vt}χ~kvt。然后,我们理论上计算出这 KKK 个虚拟位置的传统PSF (使用公式 14),记为 Pk(χ~kvt)P_{k}(\tilde{\chi}_{k}^{vt})Pk(χ~kvt)。通过归一化和阈值化 (公式 15, 16),我们将这些PSF转换成 KKK 个二值掩膜 (Mask) P~k\tilde{P}_{k}P~k。
P‾k=I[P‾k≤β]\overline{P}_{k}=\mathbb{I}_{[\overline{P}_{k}\le\beta]}Pk=I[Pk≤β]
这些掩膜 P~k\tilde{P}_{k}P~k 的“亮斑”区域(值为1)正对应着 KKK 个假设的虚警位置的主瓣。 - 掩膜操作:我们将这 KKK 个掩膜相加,然后与原始虚警图像 IoI_oIo 的幅度进行元素级相乘 (Hadamard 积 ⊙\odot⊙):
Imask(x~t)=∣Io∣⊙(P~1+P~2+P~3)I_{mask}(\tilde{x}_{t})=|I_{o}|\odot(\tilde{P}_{1}+\tilde{P}_{2}+\tilde{P}_{3})Imask(x~t)=∣Io∣⊙(P~1+P~2+P~3)
这个操作 (公式 17) 的含义是:只保留 IoI_oIo 中位于假设的虚警位置的能量,其余部分全部清零。 - 能量关联:最后,我们将掩膜后图像 ImaskI_{mask}Imask 中的所有能量求和,并将这个总能量值赋给假设的真实位置 x~t\tilde{x}_{t}x~t:
Ie(x~t)=1NxTImask(x~t)1Ny\mathcal{I}_{e}(\tilde{x}_{t})=1_{N_{x}}^{T}I_{mask}(\tilde{x}_{t})1_{N_{y}}Ie(x~t)=1NxTImask(x~t)1Ny
工作原理:
- 当 x~t≠xt\tilde{x}_{t} \ne x_tx~t=xt 时:我们生成的掩膜 P~k\tilde{P}_{k}P~k 的位置,与 IoI_oIo 中 真实的 虚警峰值位置 χkvt\chi_{k}^{vt}χkvt 错开。IoI_oIo 中的峰值能量被掩膜清零,因此 Ie(x~t)\mathcal{I}_{e}(\tilde{x}_{t})Ie(x~t) 的值很小。
- 当 x~t=xt\tilde{x}_{t} = x_tx~t=xt 时:我们生成的掩膜 P~k\tilde{P}_{k}P~k 的位置 精确地 覆盖了 IoI_oIo 中所有 KKK 个真实的虚警峰值。公式 (17) 会将这 KKK 个峰值的能量全部“提取”出来。公式 (18) 再将这 KKK 份能量非相干地(因为是对幅度 ∣Io∣|I_o|∣Io∣ 求和)累加到 Ie(xt)\mathcal{I}_{e}(x_t)Ie(xt) 这一点上,形成一个强烈的峰值。
两种方法的对比:
- 数据域:计算上更优。它是相干累加,理论上SNR增益更高。但弱点是,如果多径信号因相位问题非相干(例如相消),它就会失败。
- 图像域:计算量稍大(需要先生成 IoI_oIo)。它是非相干累加。这使它对多径的非相干性不敏感,更加鲁棒。
C. 非理想场景:粗糙墙面 (Rough Walls)
实际的墙面不是理想的镜面。如下图3所示,粗糙的墙面会产生“漫反射” (Diffuse multipath)。
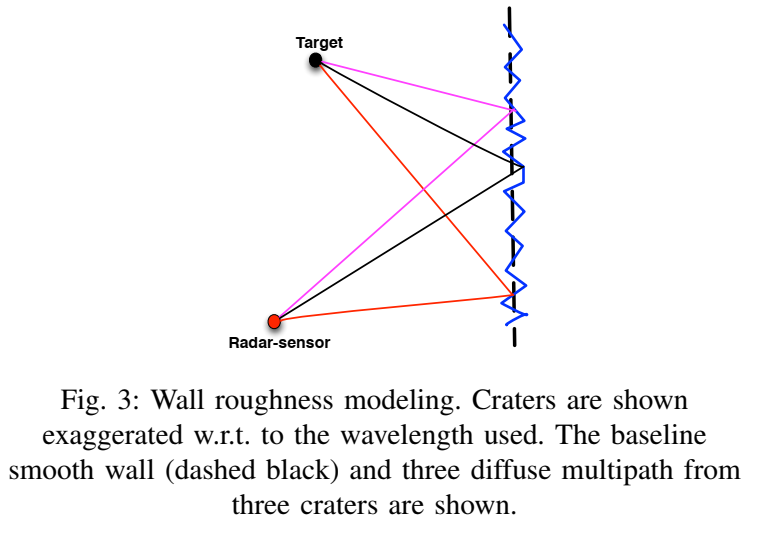
文章通过将墙面建模为 NNN 个随机深度的“子反射体” (subreflectors) 来模拟这种效应。每个子反射体的位置 xnrx_{nr}xnr 遵从高斯分布 xnr∼N(dxr,ηλ)x_{nr}\sim\mathcal{N}(d_{xr},\eta\lambda)xnr∼N(dxr,ηλ)。最终的漫反射回波是 NNN 个子反射体回波的加权和:
∑n=1NG(n)s(t−2τn)\sum_{n=1}^{N}\mathcal{G}(n)s(t-2\tau_{n})n=1∑NG(n)s(t−2τn)
其中权重 G(n)\mathcal{G}(n)G(n) 使得靠近镜面反射点的子反射体贡献更大。这种效应会导致多径信号在距离上“拖尾”或“展宽”。
仿真验证 (Simulations)
文章通过一系列仿真验证了算法的有效性。
理想场景
图4 (城市峡谷) 和 图5 (T形交叉口) 展示了核心结果。
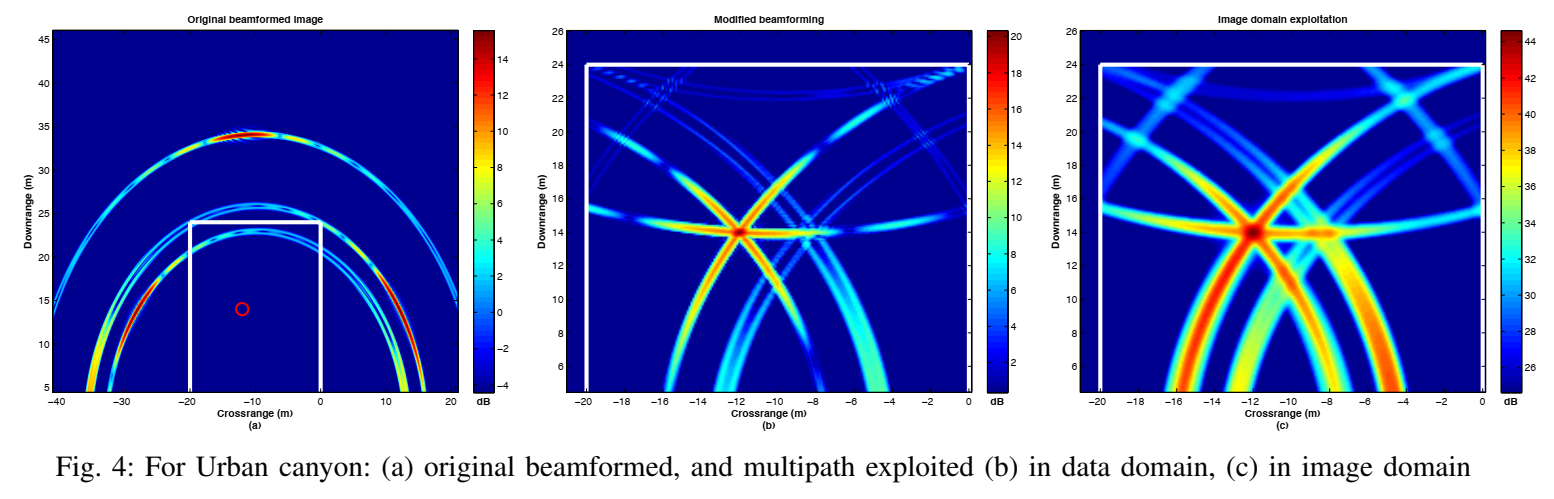
- 图 4(a) 原始图像:如理论所预测,峡谷内部(白色方框)没有目标。相反,在峡谷外部出现了三个清晰的“虚警”弧线,它们正是三个虚拟目标 xkvtx_k^{vt}xkvt 的成像。
- 图 4(b) 数据域:效果惊人。三个虚警弧线被“折叠”回了峡谷内部,并精确地相交于一点——即目标 xtx_txt 的真实位置,形成了一个极其尖锐的峰值。
- 图 4© 图像域:得到了几乎相同的结果。虚警的能量被成功“提取”并“映射”回 xtx_txt 的真实位置。
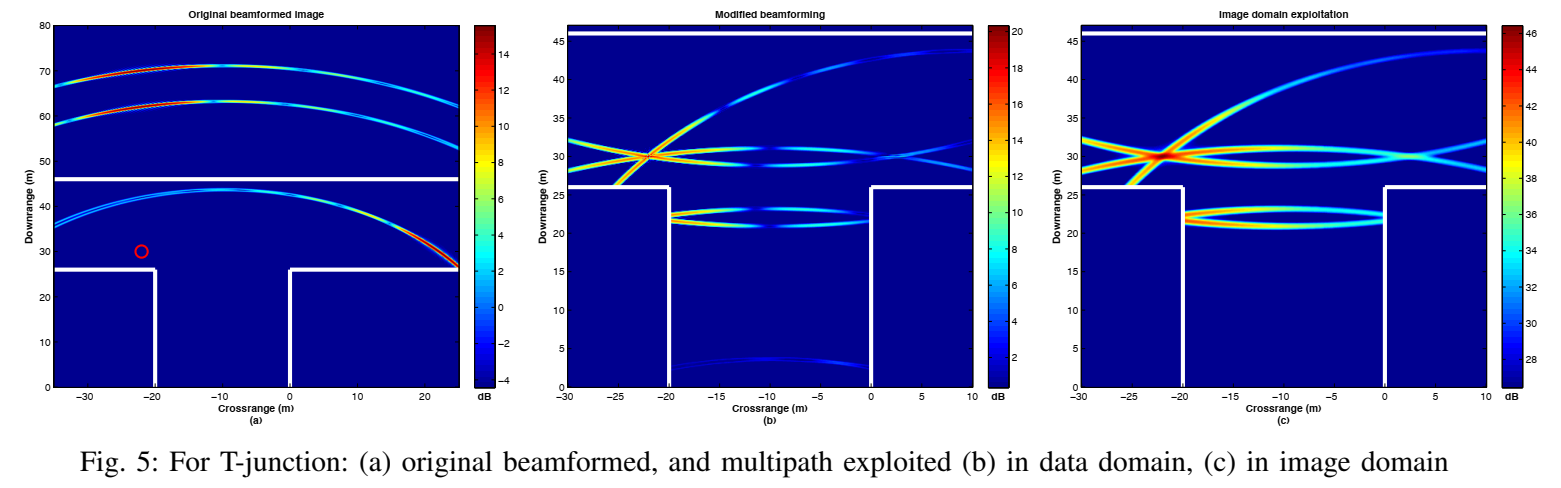
- 图 5(a) 原始图像:目标 xtx_txt (红圈 ‘o’ 所示) 未被检测到。图像在T形交叉口内部的另一侧显示了一个虚警(来自墙1的反射),这具有高度迷惑性。
- 图 5(b) 和 © :两种利用技术都成功地将所有虚警(包括那个在内部的)的能量重新定位到了 xtx_txt 的真实位置,实现了在拐角后的探测。
关键非理想场景
- 非相干多径 (Incoherent Multipath)
如图7所示,当多径信号由于相位问题相互抵消时:
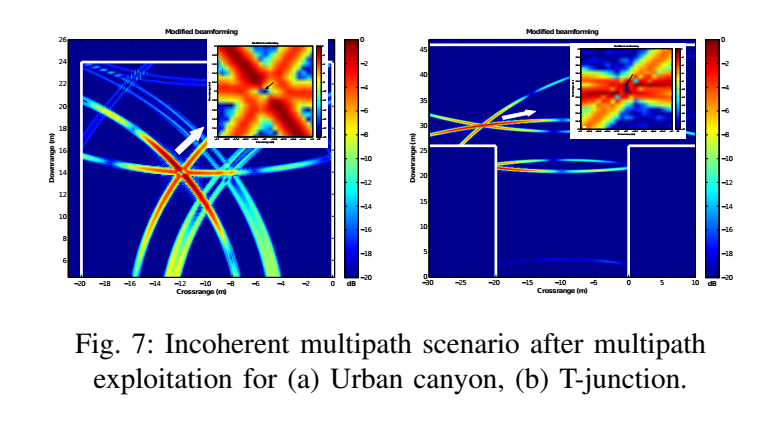
* **数据域方法 (a, b)** 失败了。在目标真实位置出现了一个“空洞”或“零点”(见图中放大的插图)。* 文章指出,**图像域方法**(未显示)在这种情况下依然**鲁棒**,因为它累加的是幅度,不受相位影响。
- 噪声、杂波和CFAR检测
图10和图11是在强噪声 (SNR=3dB) 和多个杂波目标(有LOS)的环境下进行的仿真。
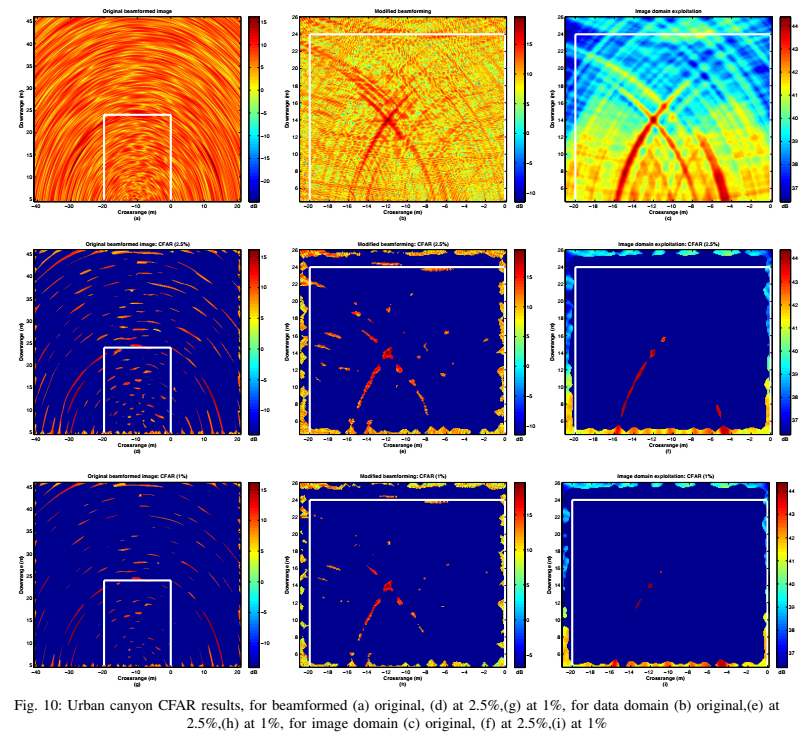
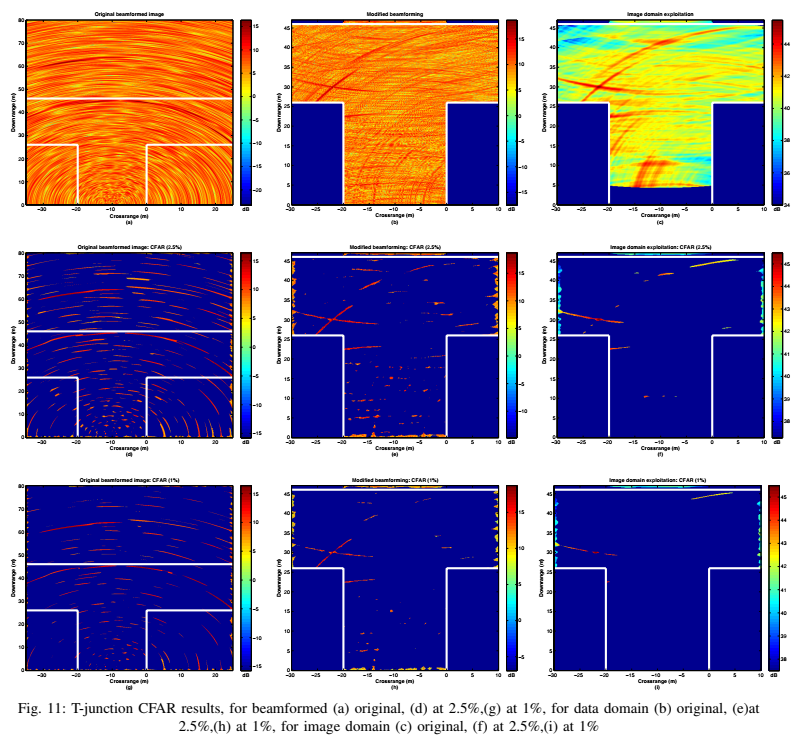
* **原始图像 (a)** 几乎被噪声淹没。* **原始图像+CFAR (d, g)** :传统的CFAR检测器在噪声和杂波上产生了大量的虚警。* **利用技术+CFAR (e, f, h, i)**:在应用了数据域或图像域技术后,CFAR检测器**成功地检测到了真实的、被遮挡的目标**,并且(在峡谷场景中)有效抑制了那些有LOS的杂波目标(因为它们的信号模式与算法所寻找的多径模式不匹配),显著降低了虚警率。
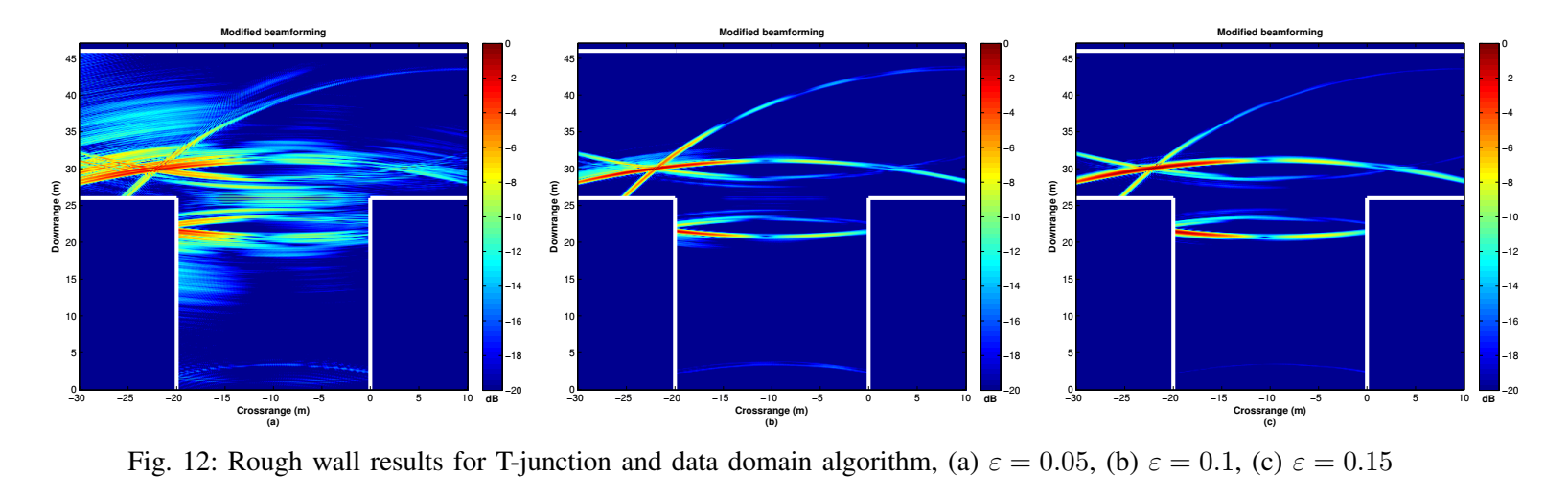
- 粗糙墙面 (Wall Roughness)
如图12所示,当墙面粗糙时,漫反射导致成像结果(原先清晰的弧线)在距离维上被“涂抹”或“展宽”。这会降低算法的聚焦性能。
- 墙面位置不精确 (Inaccuracies in wall positions)
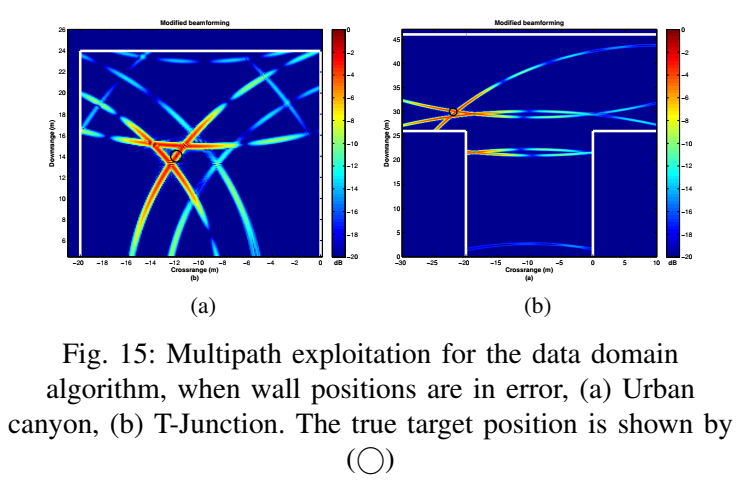
这是本文最重要的限制性因素。如果“已知”的几何信息是错误的(例如,墙的位置有 $\pm 0.5m$ 的误差),会发生什么?**图 15** 显示了结果:数据域算法“折叠”回来的多径轨迹**不再相交于同一点**。这导致相干累加的增益(数据域)或能量关联(图像域)的效果大幅下降,在真实目标位置 $x_t$ (图中 'o' 所示) 的SNR增益显著降低。为了量化这种不确定性,附录B(在图16和17中展示)提出了一个**敏感性分析框架**:
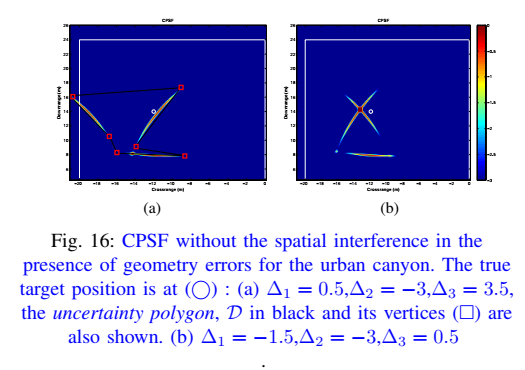
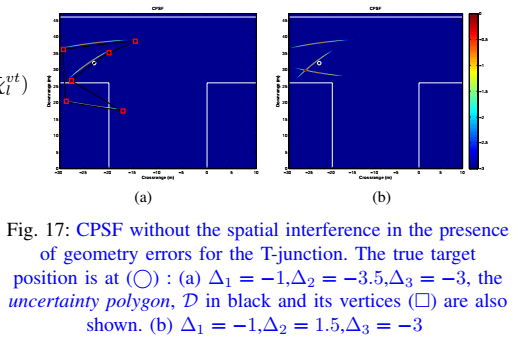
* 它首先计算每个*受误差影响的*多径 $\mathcal{Q}_{ck}$ (公式 24) 的主瓣区域 $\mathcal{A}_k$ (公式 25)。* **情况1(图b)**:如果这些区域 $\mathcal{A}_k$ 仍然存在交集 $\mathcal{B}$ (公式 26),则交集点仍可被视为目标位置(尽管有偏差)。* **情况2(图a)**:如果这些区域*不再相交*,算法会定义一个“**不确定性多边形**” (Uncertainty Polygon) $\mathcal{D}$ (公式 27),该多边形包含了所有分离的主瓣。此时,算法只能报告目标位于这个多边形*区域*内,而无法精确定位。
结论 (Conclusions)
本文成功地提出了两种在NLOS(非视距)城市环境下利用多径信号探测和定位隐藏目标的SAR算法(数据域和图像域)。仿真表明,这些技术能有效“解开”多径造成的虚警,将其重新聚焦到目标的真实位置,从而在抑制虚警的同时提高目标的SCR。然而,本文也揭示了一个关键的实践挑战:这些利用技术目前高度依赖于对环境(墙面)几何位置的精确先验知识。
附录:矩形波形的PSF与CPSF数学推导
原文的附录A提供了当发射波形 p(t)p(t)p(t) 为标准矩形脉冲时,PSF和CPSF的具体数学形式。
假设基带波形 p(t)p(t)p(t) 是一个宽度为 TTT 的矩形函数:
p(t)=rect(t/T):={10≤t≤T0otherwisep(t)=rect(t/T):=\begin{cases}1&0\le t\le T\\ 0&otherwise\end{cases}p(t)=rect(t/T):={100≤t≤Totherwise
其傅里叶变换 P(ω)P(\omega)P(ω) 为:
P(ω)=T⋅exp(−jωT/2)⋅Sinc(ωT/2π)P(\omega)=T \cdot exp(-j\omega T/2) \cdot Sinc(\omega T/2\pi)P(ω)=T⋅exp(−jωT/2)⋅Sinc(ωT/2π)
1. 传统PSF推导 (针对矩形波)
将 P(ω)P(\omega)P(ω) 代入通用的PSF公式 (14) 中。公式的核心是 ∣P(ω−ωc)∣2|P(\omega-\omega_c)|^2∣P(ω−ωc)∣2 的逆傅里叶变换,这对应于 p(t)p(t)p(t) 的自相关函数,即一个宽度为 2T2T2T 的三角波。
经过推导,特定于矩形波的PSF Pr(xt,x)\mathcal{P}^{r}(x_{t},x)Pr(xt,x) (公式 19) 可以写为:
Pr(xt,x)=∑m=1MΨ(Δτm(xt;x))\mathcal{P}^{r}(x_{t},x)=\sum_{m=1}^{M}\Psi(\Delta\tau_{m}(x_{t};x))Pr(xt,x)=m=1∑MΨ(Δτm(xt;x))
其中 Ψ(⋅)\Psi(\cdot)Ψ(⋅) (公式 20) 就是这个三角波函数,它只在 ∣Δτm∣≤T|\Delta\tau_m| \le T∣Δτm∣≤T 时非零:
Ψ(Δτm(xt;x)):={Φ1(⋅)∣ΔRm(xt;x)∣ΔR≤10otherwise\Psi(\Delta\tau_{m}(x_{t};x)):=\begin{cases}\Phi_{1}(\cdot)&\frac{|\Delta R_{m}(x_{t};x)|}{\Delta R}\le1\\ 0&otherwise\end{cases}Ψ(Δτm(xt;x)):={Φ1(⋅)0ΔR∣ΔRm(xt;x)∣≤1otherwise
Φ1(⋅)\Phi_{1}(\cdot)Φ1(⋅) (公式 25) 是三角波的幅度和相位:
Φ1(⋅)=T(1−∣ΔRm(xt;x)∣ΔR)exp(−jωc2Δτm(xt;x))\Phi_{1}(\cdot)=T(1-\frac{|\Delta R_{m}(x_{t};x)|}{\Delta R})exp(-j\omega_{c}2\Delta\tau_{m}(x_{t};x))Φ1(⋅)=T(1−ΔR∣ΔRm(xt;x)∣)exp(−jωc2Δτm(xt;x))
这里的关键参数是 ΔR=cT/2=c/2B\Delta R = cT/2 = c/2BΔR=cT/2=c/2B (其中 B≈1/TB \approx 1/TB≈1/T 是带宽),它代表了系统的距离分辨率。这个公式清晰地显示了PSF在距离维上是一个幅度按三角形状衰减的脉冲,并携带由时延 Δτm\Delta\tau_mΔτm 引起的载波相位。
2. CPSF推导 (针对矩形波)
采用完全相同的逻辑,将 P(ω)P(\omega)P(ω) 代入通用的CPSF公式 (12),我们得到特定于矩形波的CPSF Pcr(xt,x)\mathcal{P}_{c}^{r}(x_{t},x)Pcr(xt,x) (公式 21):
Pcr(xt,x)=∑m=1M∑k=13∑l=13Ψ(Δτmkl(χkvt;χ‾lvt))\mathcal{P}_{c}^{r}(x_{t},x)=\sum_{m=1}^{M}\sum_{k=1}^{3}\sum_{l=1}^{3}\Psi(\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt}))Pcr(xt,x)=m=1∑Mk=1∑3l=1∑3Ψ(Δτmkl(χkvt;χlvt))
这里的 Ψ(⋅)\Psi(\cdot)Ψ(⋅) (公式 22) 是完全相同的三角波函数,只是其自变量变为了多径时延差 Δτmkl\Delta\tau_{mkl}Δτmkl:
Ψ(Δτmkl(χkvt;χ‾lvt)):={Φ2(⋅)∣ΔRmkl(χkvt;χ‾lvt)∣ΔR≤10otherwise\Psi(\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt})):=\begin{cases}\Phi_{2}(\cdot)&\frac{|\Delta R_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt})|}{\Delta R}\le1\\ 0&otherwise\end{cases}Ψ(Δτmkl(χkvt;χlvt)):={Φ2(⋅)0ΔR∣ΔRmkl(χkvt;χlvt)∣≤1otherwise
其幅度和相位 Φ2(⋅)\Phi_{2}(\cdot)Φ2(⋅) (公式 645) 形式也相同:
Φ2(⋅)=T(1−∣ΔRmkl(χkvt;χl‾vt)∣ΔR)exp(−jωc2Δτmkl(χkvt;χl‾vt)\Phi_{2}(\cdot)=T(1-\frac{|\Delta R_{mkl}(\chi_{k}^{vt};\overline{\chi_{l}}^{vt})|}{\Delta R})exp(-j\omega_{c}2\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi_{l}}^{vt})Φ2(⋅)=T(1−ΔR∣ΔRmkl(χkvt;χlvt)∣)exp(−jωc2Δτmkl(χkvt;χlvt)
3. 干扰项 (Interference Term)
有了这些形式,我们就可以明确写出CPSF中的干扰项 (公式 23)。它等于总的CPSF减去期望项 (即 k=lk=lk=l 的项):
Pc(xt,x)−Qc(xt,x)=∑m=1M∑k=13∑l=1,l≠k3Ψ(Δτmkl(χkvt;χ‾lvt))\mathcal{P}_{c}(x_{t},x)-\mathcal{Q}_{c}(x_{t},x) = \sum_{m=1}^{M}\sum_{k=1}^{3}\sum_{l=1, l\ne k}^{3}\Psi(\Delta\tau_{mkl}(\chi_{k}^{vt};\overline{\chi}_{l}^{vt}))Pc(xt,x)−Qc(xt,x)=m=1∑Mk=1∑3l=1,l=k∑3Ψ(Δτmkl(χkvt;χlvt))
这个公式表明,数据域算法中的空间干扰(鬼影)是由不同多径路径 (k≠lk \ne lk=l) 之间的时延差 Δτmkl\Delta\tau_{mkl}Δτmkl 决定的。当这个时延差小于一个距离分辨率(即 ∣ΔRmkl∣≤ΔR|\Delta R_{mkl}| \le \Delta R∣ΔRmkl∣≤ΔR)时,Ψ(⋅)\Psi(\cdot)Ψ(⋅) 非零,就会产生干扰。仿真(图8)表明,这些干扰项通常是空间扩展的,其幅度与传统PSF的旁瓣电平相当。
