当前位置：首页 > news >正文

【机器学习】k近邻法

news 2025/10/25 6:55:33

一、引言

二、k 近邻算法

算法 1：k 近邻法

三、k 近邻模型

（一）模型

（二）距离度量

（三）k值的选择

（四）分类决策规则

四、k 近邻法的实现：kd 树

（一）构造 kd 树

算法2：构造平衡 kd 树

（二）搜索 kd 树

算法3：用 kd 树的最近邻搜索

例题：二维空间 kd 树构造

五、总结

一、引言

k 近邻法（k-nearest neighbor，k-NN）是一种基本分类与回归方法。k 近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可多类。k 近邻法假设给定训练数据集，其中实例类别已定。分类时，对新实例，根据其k个最近邻的训练实例类别，通过多数表决等方式预测。故 k 近邻法无显式学习过程，实际利用训练数据集划分特征向量空间并作为分类 “模型”。k值选择、距离度量及分类决策规则是其三个基本要素，该方法于 1968 年由 Cover 和 Hart 提出。本文先叙述 k 近邻算法，再讨论其模型及三个基本要素，最后讲述实现方法 ——kd 树，介绍构造和搜索 kd 树的算法，并用Python代码完整实现。

二、k 近邻算法

k 近邻算法简单直观：给定训练数据集，对新输入实例，在训练数据集中找与其最邻近的k个实例，若这k个实例多数属于某类，就将该输入实例归为该类。

算法 1：k 近邻法

输入：训练数据集

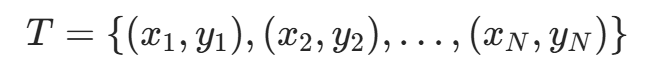
其中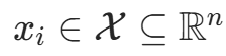，为实例的特征向量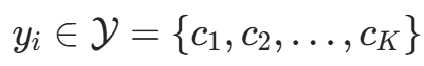，为实例的类别，i=1,2,…,N；实例特征向量x。输出：实例x所属的类y。

(1) 据给定距离度量，在训练集T中找出与x最邻近的k个点，涵盖这k个点的x的邻域记作 $N_k(x)$ ；

(2) 在 $N_k(x)$ 中据分类决策规则（如多数表决）决定x的类别y：

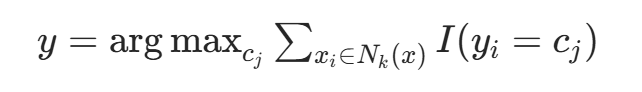
其中，I为指示函数， $y_i=c_j$ 时I为 1，否则为 0。

k 近邻法的模型对应特征空间的划分，由距离度量、k值选择和分类决策规则三个基本要素决定。

三、k 近邻模型

（一）模型

k 近邻法中，训练集、距离度量、k值及分类决策规则确定后，新输入实例的类别唯一确定。这相当于将特征空间划分为若干子空间，子空间内每个点的类别确定。特征空间中，每个训练实例点 $x_i$ 的邻近区域（单元）内的点类别为 $y_i$ ，所有训练实例点的单元构成特征空间的划分。

（二）距离度量

特征空间中两实例点的距离反映其相似程度。k 近邻模型的特征空间常为n维实数向量空间，常用欧氏距离，也可用更一般的 $L_p$ 距离或 Minkowski 距离。

设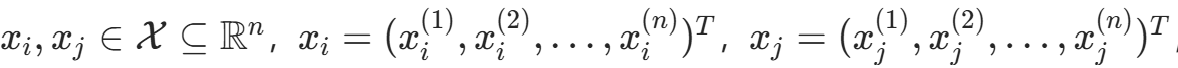，则 $L_p$ 距离定义为：

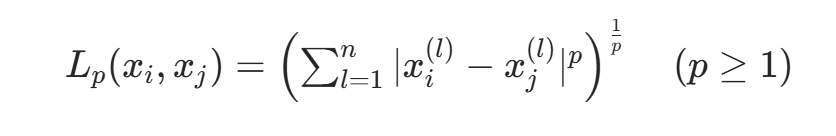
当p=2时，为欧氏距离：
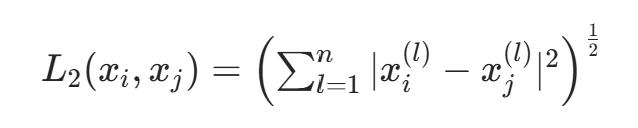
当p=1时，为曼哈顿距离：
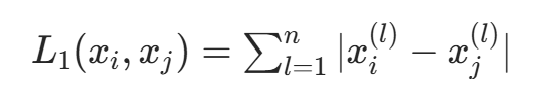
当p=∞时，为各坐标距离的最大值：

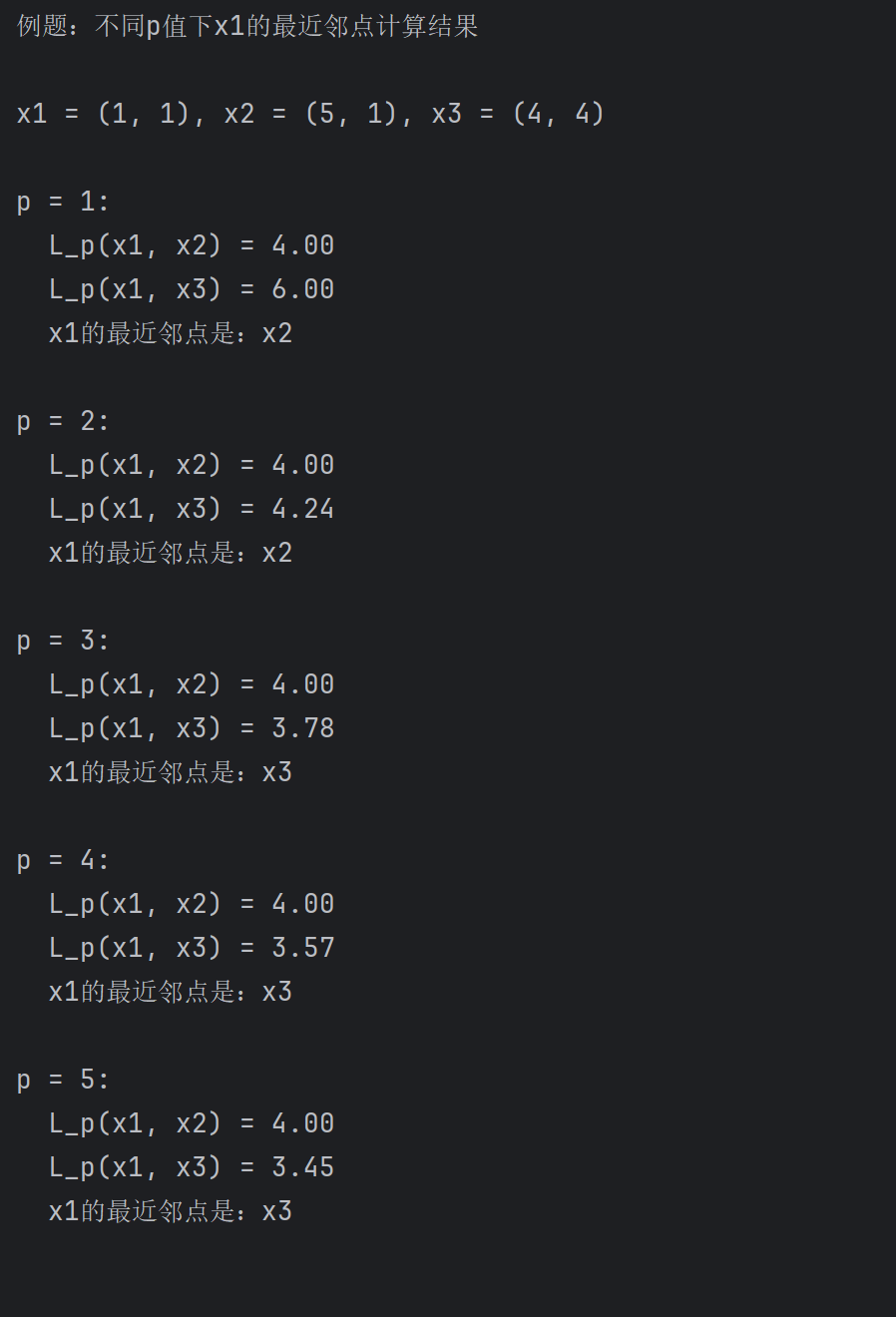
例题：已知二维空间的 3 个点 x₁=(1,1)ᵀ，x₂=(5,1)ᵀ，x₃=(4,4)ᵀ，试求在 p 取不同值时，L_p 距离下 x₁的最近邻点。

解：因为 x₁和 x₂只有第一维的值不同，所以 p 为任何值时，L_p (x₁,x₂)=4。而 L₁(x₁,x₃)=6，L₂(x₁,x₃)=4.24，L₃(x₁,x₃)=3.78，L₄(x₁,x₃)=3.57于是得到：p 等于 1 或 2 时，x₂是 x₁的最近邻点；p 大于等于 3 时，x₃是 x₁的最近邻点。

Python代码完整实现：

import mathdef lp_distance(x, y, p):"""计算两个二维点x和y之间的L_p距离参数:x: 第一个点的坐标，元组或列表 (x1, x2)y: 第二个点的坐标，元组或列表 (y1, y2)p: 距离度量参数 (p≥1)返回:两点间的L_p距离"""# 计算各维度差的绝对值的p次方之和sum_p = (abs(x[0] - y[0]) ** p) + (abs(x[1] - y[1]) ** p)# 开p次方根return sum_p ** (1 / p)if __name__ == "__main__":# 定义题目中的三个点x1 = (1, 1)x2 = (5, 1)x3 = (4, 4)# 测试不同p值（包含题目中的p=1,2,3,4及额外p=5验证结论）p_values = [1, 2, 3, 4, 5]print("例题：不同p值下x1的最近邻点计算结果\n")print(f"x1 = {x1}, x2 = {x2}, x3 = {x3}\n")for p in p_values:# 计算x1到x2和x1到x3的L_p距离d_x1x2 = lp_distance(x1, x2, p)d_x1x3 = lp_distance(x1, x3, p)# 判断最近邻点if d_x1x2 < d_x1x3:nearest = "x2"else:nearest = "x3"# 格式化输出（保留2位小数）print(f"p = {p}:")print(f"  L_p(x1, x2) = {d_x1x2:.2f}")print(f"  L_p(x1, x3) = {d_x1x3:.2f}")print(f"  x1的最近邻点是：{nearest}\n")

程序运行截图展示：

（三）k值的选择

k值选择对 k 近邻法结果影响重大。

选较小k值：用较小邻域的训练实例预测，近似误差减小，但估计误差增大，模型复杂，易过拟合。
选较大k值：用较大邻域的训练实例预测，估计误差减小，但近似误差增大，模型简单。
若k=N：预测为训练实例中最多的类，模型过简，忽略大量有用信息，不可取。

应用中k值一般取较小值，常用交叉验证法选最优k值。

（四）分类决策规则

k 近邻法的分类决策规则常为多数表决，即由输入实例的k个邻近训练实例的多数类决定输入实例的类。

多数表决规则可解释为：若分类损失函数为 0-1 损失函数，分类函数f: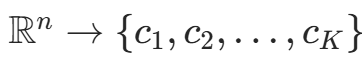，则误分类概率为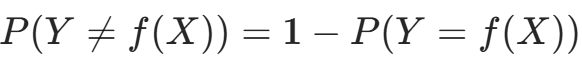。对实例x，其最近邻的k个训练实例点构成 $N_k(x)$ ，若 $N_k(x)$ 区域类别为 $c_j$ ，则误分类率为：

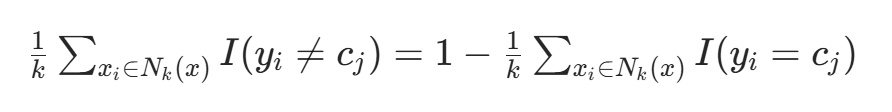
要使误分类率最小（经验风险最小），需使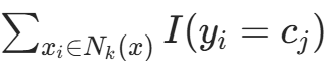最大，故多数表决规则等价于经验风险最小化。

四、k 近邻法的实现：kd 树

实现 k 近邻法时，需解决训练数据的快速 k 近邻搜索问题，尤其在特征空间维数大、训练数据容量大时。

k 近邻法最简单的实现是线性扫描，即计算输入实例与每个训练实例的距离。但训练集大时计算耗时，不可行。

为提高搜索效率，可采用特殊结构存储训练数据以减少距离计算次数。

Python代码初始化kd树：

class Node:def __init__(self, axis=None, value=None, left=None, right=None, point=None):self.axis = axis  # 分割维度self.value = value  # 分割值self.left = left    # 左子节点self.right = right  # 右子节点self.point = point  # 叶节点对应的实际点

（一）构造 kd 树

kd 树是一种对 k 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd 树是二叉树，表示对 k 维空间的一个划分（partition）。构造 kd 树相当于不断地用垂直于坐标轴的超平面将 k 维空间切分，构成一系列的 k 维超矩形区域。kd 树的每个结点对应于一个 k 维超矩形区域。

构造 kd 树的方法如下：构造根结点，使根结点对应于 k 维空间中包含所有实例点的超矩形区域；通过下面的递归方法，不断地对 k 维空间进行切分，生成子结点。在超矩形区域（结点）上选择一个坐标轴和在此坐标轴上的一个切分点，确定一个超平面，这个超平面通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域（子结点）；这时，实例被分到两个子区域。这个过程直到子区域内没有实例时终止（终止时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。

通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的 ** 中位数（median）** 为切分点，这样得到的 kd 树是平衡的。注意，平衡的 kd 树搜索时的效率未必是最优的。

算法2：构造平衡 kd 树

输入：k维空间数据集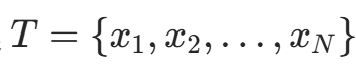，其中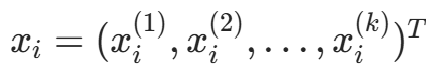，i=1,2,…,N；输出：kd 树。

构造根结点：根结点对应包含T的k维空间超矩形区域。选择 $x^{(1)}$ 为坐标轴，以T中所有实例的 $x^{(1)}$ 坐标的中位数为切分点，通过切分点且与 $x^{(1)}$ 垂直的超平面将根结点区域切分为两个子区域。生成深度为 1 的左、右子结点：左子结点对应 $x^{(1)}$ 小于切分点的子区域，右子结点对应 $x^{(1)}$ 大于切分点的子区域；落在切分平面上的实例点保存在根结点。
递归切分：对深度为j的结点，选择 $x^{(l)}$ 为切分坐标轴（l=jmodk+1），以该结点区域内所有实例的 $x^{(l)}$ 坐标的中位数为切分点，通过切分点且与 $x^{(l)}$ 垂直的超平面将区域切分为两个子区域。生成深度为j+1的左、右子结点（左子结点对应 $x^{(l)}$ 小于切分点的子区域，右子结点对应 $x^{(l)}$ 大于切分点的子区域）；落在切分平面上的实例点保存在该结点。
终止条件：直到两个子区域无实例存在时停止，形成 kd 树的区域划分。

Python代码构造kd树：

def build_kd_tree(points, depth=0):"""递归构造kd树"""if not points:return Nonek = len(points[0])  # 特征维度axis = depth % k    # 轮流选择分割维度# 按当前维度排序points_sorted = sorted(points, key=lambda x: x[axis])median_idx = len(points_sorted) // 2  # 取中位数索引median_point = points_sorted[median_idx]# 递归构造左右子树left = build_kd_tree(points_sorted[:median_idx], depth + 1)right = build_kd_tree(points_sorted[median_idx+1:], depth + 1)return Node(axis=axis, value=median_point[axis], left=left, right=right, point=median_point)

（二）搜索 kd 树

利用 kd 树进行 k 近邻搜索时，以最近邻为例：

定位叶结点：从根结点出发，递归向下访问 kd 树，直到找到包含目标点的叶结点，以此叶结点的实例点作为当前最近点。
回退父结点：目标点的最近邻一定在以目标点为中心、以 “当前最近点” 距离为半径的超球体内。回退到父结点，检查父结点的另一子结点的超矩形区域是否与超球体相交：
- 若相交，在该子区域内递归搜索更近的点，更新 “当前最近点”；
- 若不相交，继续回退，直到根结点，最终 “当前最近点” 即为目标点的最近邻。

算法3：用 kd 树的最近邻搜索

输入：已构造的 kd 树，目标点x；输出：x的最近邻。

定位叶结点：从根结点出发，递归向下访问 kd 树。若目标点x当前维的坐标小于切分点坐标，移动到左子结点，否则移动到右子结点，直到子结点为叶结点。
初始化当前最近点：以该叶结点为 “当前最近点”。
递归回退父结点：
- 若该结点实例点比 “当前最近点” 更近，更新 “当前最近点”；
- 检查父结点的另一子结点对应的区域是否与以目标点为球心、以 “当前最近点” 距离为半径的超球体相交：
  - 若相交，移动到该子结点，递归搜索最近邻；
  - 若不相交，向上回退。
终止条件：回退到根结点时，搜索结束，最终 “当前最近点” 即为x的最近邻。

Python代码搜索kd树：

def distance(a, b):"""计算欧氏距离"""return math.sqrt(sum((ai - bi)** 2 for ai, bi in zip(a, b)))def find_nearest_neighbor(root, point, depth=0, best=None, best_dist=float('inf')):"""递归搜索最近邻"""if root is None:return best, best_distk = len(point)axis = root.axis# 向下遍历到叶节点if point[axis] < root.value:next_node = root.leftother_node = root.rightelse:next_node = root.rightother_node = root.leftbest, best_dist = find_nearest_neighbor(next_node, point, depth + 1, best, best_dist)# 检查当前节点dist = distance(root.point, point)if dist < best_dist:best = root.pointbest_dist = dist# 检查另一子树（超球体与超矩形相交时）if abs(point[axis] - root.value) < best_dist:best, best_dist = find_nearest_neighbor(other_node, point, depth + 1, best, best_dist)return best, best_dist

例题：二维空间 kd 树构造

给定数据集：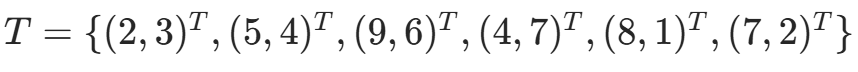

选择 $x^{(1)}$ 轴，6 个数据点的x(1)坐标中位数为 7，以平面 $x^{(1)}$ =7将空间分为左、右子矩形；
左矩形以 $x^{(2)}$ =4切分，右矩形以 $x^{(2)}$ =6切分；
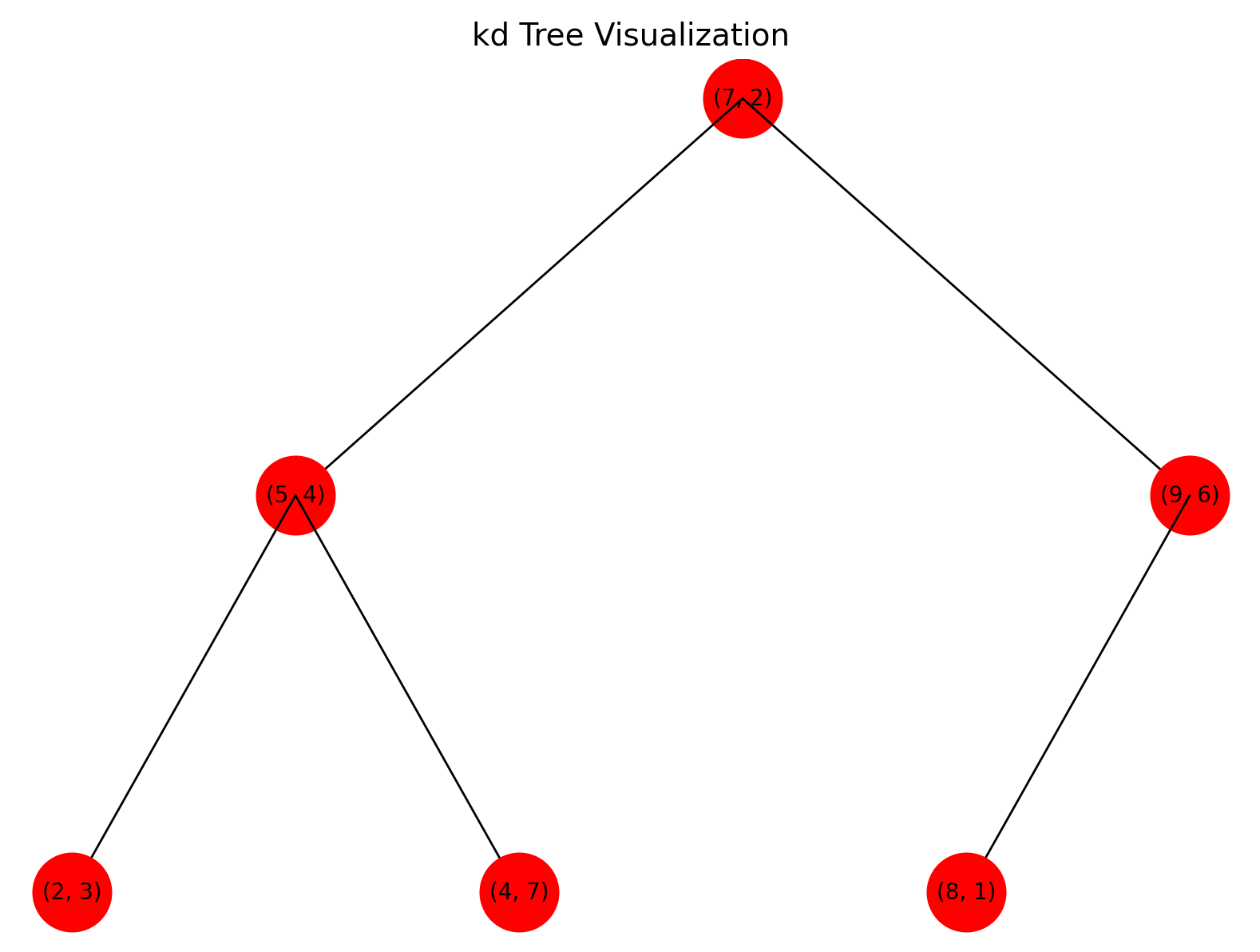
递归操作后，得到特征空间划分和 kd 树（根结点(7,2)，左子结点(5,4)，右子结点(9,6)；(5,4)的左子结点(2,3)、右子结点(4,7)；(9,6)的子结点(8,1)）。

求点 $x=(3,4.5)^T$ 的最近邻点。

Python完整代码如下：

import matplotlib.pyplot as plt
import mathclass Node:def __init__(self, axis=None, value=None, left=None, right=None, point=None):self.axis = axis  # 分割维度self.value = value  # 分割值self.left = left    # 左子节点self.right = right  # 右子节点self.point = point  # 叶节点对应的实际点def build_kd_tree(points, depth=0):"""递归构造kd树"""if not points:return Nonek = len(points[0])  # 特征维度axis = depth % k    # 轮流选择分割维度# 按当前维度排序points_sorted = sorted(points, key=lambda x: x[axis])median_idx = len(points_sorted) // 2  # 取中位数索引median_point = points_sorted[median_idx]# 递归构造左右子树left = build_kd_tree(points_sorted[:median_idx], depth + 1)right = build_kd_tree(points_sorted[median_idx+1:], depth + 1)return Node(axis=axis, value=median_point[axis], left=left, right=right, point=median_point)def distance(a, b):"""计算欧氏距离"""return math.sqrt(sum((ai - bi)** 2 for ai, bi in zip(a, b)))def find_nearest_neighbor(root, point, depth=0, best=None, best_dist=float('inf')):"""递归搜索最近邻"""if root is None:return best, best_distk = len(point)axis = root.axis# 向下遍历到叶节点if point[axis] < root.value:next_node = root.leftother_node = root.rightelse:next_node = root.rightother_node = root.leftbest, best_dist = find_nearest_neighbor(next_node, point, depth + 1, best, best_dist)# 检查当前节点dist = distance(root.point, point)if dist < best_dist:best = root.pointbest_dist = dist# 检查另一子树（超球体与超矩形相交时）if abs(point[axis] - root.value) < best_dist:best, best_dist = find_nearest_neighbor(other_node, point, depth + 1, best, best_dist)return best, best_distdef plot_kd_tree(node, x=0.5, y=1, depth=0, parent_x=None, parent_y=None, ax=None):"""递归绘制kd树结构"""if ax is None:ax = plt.gca()if node is None:return# 绘制当前节点与父节点的连线if parent_x is not None and parent_y is not None:ax.plot([parent_x, x], [parent_y, y], 'k-', linewidth=1)# 绘制节点（红色圆点）ax.plot(x, y, 'ro', markersize=35)# 标注节点坐标ax.text(x, y, str(node.point), ha='center', va='center', fontsize=10)# 递归处理左右子树，调整x坐标以避免重叠k = len(node.point)axis = node.axisleft_x = x - 0.2 / (2 ** depth)right_x = x + 0.2 / (2 ** depth)plot_kd_tree(node.left, left_x, y - 0.1, depth + 1, x, y, ax)plot_kd_tree(node.right, right_x, y - 0.1, depth + 1, x, y, ax)# ------------------- 测试 -------------------
# 教材例3.2的数据集
points = [(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)]
root = build_kd_tree(points)# 可视化kd树
plt.figure(figsize=(8, 6))
plot_kd_tree(root)
plt.axis('off')  # 隐藏坐标轴
plt.title('kd Tree Visualization', fontsize=14)
plt.tight_layout()
plt.show()# 测试最近邻搜索
target = (3, 4.5)  # 目标点
nearest, dist = find_nearest_neighbor(root, target)
print(f"目标点 {target} 的最近邻点：{nearest}，距离：{round(dist, 2)}")

程序运行截图展示：

五、总结

本文系统介绍了k近邻算法（k-NN）及其实现方法。k-NN是一种基于实例的分类与回归方法，通过计算输入实例与训练数据的距离，选择k个最近邻点进行分类决策。文章详细阐述了k-NN的三要素：距离度量（包括欧氏、曼哈顿等）、k值选择（影响模型复杂度）和分类决策规则（如多数表决）。重点介绍了kd树这一高效实现方式，包括其构造方法（递归划分特征空间）和搜索算法（回溯查找最近邻）。通过Python代码实现了距离计算、kd树构建和最近邻搜索功能，并以二维空间示例验证了算法有效性。最后指出平衡kd树虽能提高搜索效率，但未必最优。

查看全文

http://www.dtcms.com/a/523613.html