《算法闯关指南:优选算法--二分查找》--23.寻找旋转排序数组中的最小值,24.点名

🎬 博主简介:

文章目录
- 前言:
- 23. 寻找旋转排序数组中的最小值
- 解法(二分查找):
- 算法思路:
- C++算法代码:
- 算法总结&&笔记展示:
- 24 .点名
- 解法(二分查找):
- 算法思路:
- C++算法代码:
- 算法总结&&笔记展示:
- 结尾:
前言:
聚焦算法题实战,系统讲解三大核心板块:优选算法:剖析动态规划、二分法等高效策略,学会寻找“最优解”。 递归与回溯:掌握问题分解与状态回退,攻克组合、排列等难题。 贪心算法:理解“局部最优”到“全局最优”的思路,解决区间调度等问题 内容以题带点,讲解思路与代码实现,帮助大家快速提升代码能力。
23. 寻找旋转排序数组中的最小值
题目链接:
153. 寻找旋转排序数组中的最小值 - 力扣
题目描述:
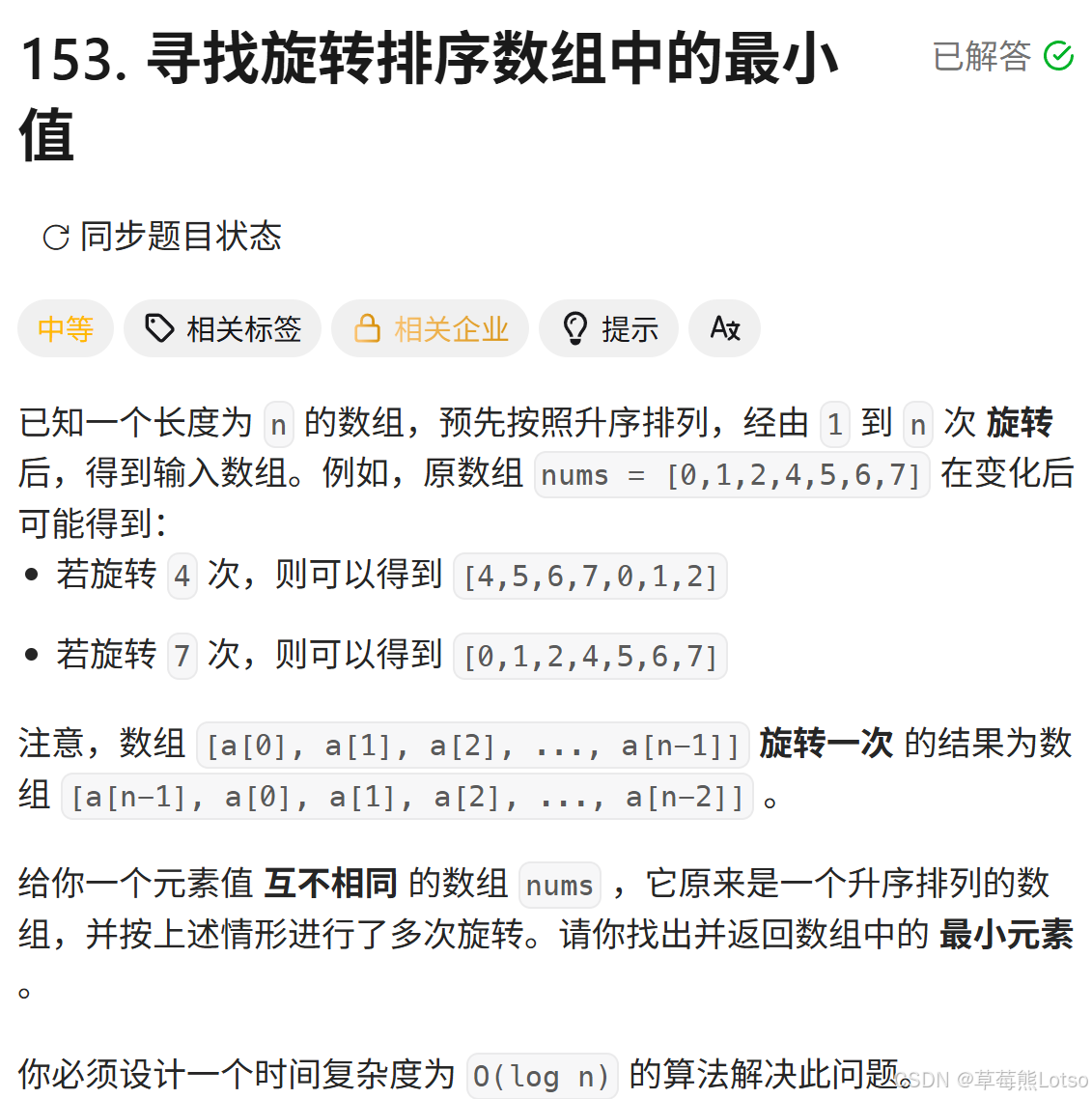
题目示例:

解法(二分查找):
算法思路:
题目中的数组规则如下图所示:
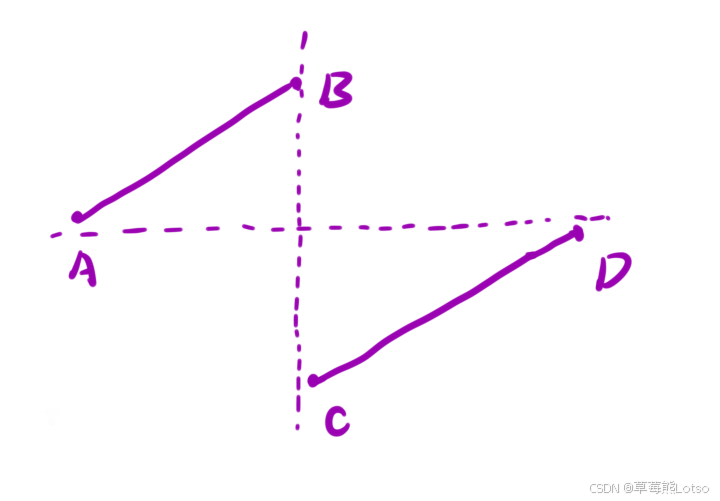
其中 c 点就是我们要求的点。
二分的本质:找到一个判断标准,使得查找区间能够一分为二。
通过图像我们可以发现,【A,B】 区间内的点都是严格大于 D 点的值的,C 点的值是严格小于 D 点的值的。但是当 【C,D】 区间只有一个元素的时候,C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left,right:
然后根据 mid 的落点,我们可以划分下一个查询的区间:
- 当
mid在【A,B】区间的时候,也就是mid位置的值严格大于D点的值,下一次查询区间在【mid+1,right】上; - 当
mid在【C,D】区间的时候,也就是mid位置的值严格小于等于D点的值,下次查询区间在【left,mid】上。
当区间长度变成 1 的时候,就是我们要找的结果。
C++算法代码:
class Solution {
public:int findMin(vector<int>& nums) {int n=nums.size();int left=0,right=n-1;if(nums[0]<=nums[n-1]){return nums[0];}while(left<right){int mid=left+(right-left)/2;if(nums[mid] >= nums[0]) left=mid+1;else right=mid;}return nums[left];}
};
算法总结&&笔记展示:
笔记字有点丑,大家见谅:

24 .点名
题目链接:
LCR 173. 点名 - 力扣(LeetCode)
题目描述:

题目示例:

解法(二分查找):
算法思路:
关于这道题中,时间复杂度为 O(N) 的解法有很多种,而且也都比较好想到,这里就不再赘述。本题我们主要介绍的是一个时间复杂度为 O(logn) 的最优解法二分法:
在这个升序的数组中,我们发现:
- 在第一个缺失位置的左边,数组内元素都是与数组下标相等的;
- 在第一个缺失位置的右边,数组内的元素都是与数组下标不相等的。
因此,我们可以利用这个 【二段性】 ,来使用 【二分查找】 算法。
C++算法代码:
class Solution {
public:int takeAttendance(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]==mid) left=mid+1;else right=mid;}if(nums[left]==left) return left+1;return left;}
};
算法总结&&笔记展示:
笔记字有点丑,大家见谅:

结尾:
🍓 我是草莓熊 Lotso!若这篇技术干货帮你打通了学习中的卡点:
👀 【关注】跟我一起深耕技术领域,从基础到进阶,见证每一次成长
❤️ 【点赞】让优质内容被更多人看见,让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好,需要时直接查、随时用
💬 【评论】分享你的经验或疑问(比如曾踩过的技术坑?),一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向,告诉大家哪个技术点最该重点拆解
技术之路难免有困惑,但同行的人会让前进更有方向~愿我们都能在自己专注的领域里,一步步靠近心中的技术目标!
结语:本文精选两道二分查找经典题型,通过图解与代码实现详解解题思路。旋转排序数组最小值:利用区间二段性,比较中点与右端点值,收缩查找范围至单个元素。缺失数字查找:根据元素值与下标关系二分,定位首个不匹配位置。笔记附手写解析,助你掌握二分核心思想——“以判断标准分割区间”,高效解决有序数据问题。
✨把这些内容吃透超牛的!放松下吧✨ ʕ˘ᴥ˘ʔ づきらど

