当前位置：首页 > news >正文

Time Interval Aware Self-Attention for Sequential Recommendation

news 来源：原创 2025/5/15 6:10:03

动机

推荐系统有两个重要的研究方向，时间推荐和序列推荐。
以前的序列推荐器会丢掉时间戳，只保留物品的顺序。然而，直观来看，时间戳更近的物品对下一个物品的影响会更大。例如，两个用户有相同的交互序列，但其中一个用户在一天内产生了这些交互，而另一个用户在一个月内完成了这些交互。因此，即使这两个用户的交互在序列中的位置相同，它们对下一个物品的影响也应该是不同的。然而，以前的序列推荐技术将这两种情况视为相同，因为它们只考虑了序列位置。

贡献

我们提议将用户的交互历史视为具有不同时间间隔的序列，并将不同的时间间隔建模为任意两次交互之间的关系。
我们结合了自注意力中绝对位置编码和相对时间间隔编码的优势，设计了一种新颖的时间间隔感知自注意力机制，以学习不同物品、绝对位置和时间间隔的权重，从而预测未来的物品。

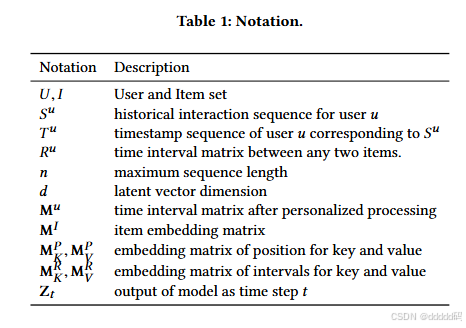
符号说明

问题公式化

设U和I分别表示用户集和项目集。在时间感知序列推荐的设定中，对于每个用户 $u\in U$ ，我们有该用户的动作序列，记为 $S^{u} = (S_{1}^{u}, S_{2}^{u}, ..., S_{|S^{u}|}^{u})$ ，其中 $S_{t}^{u} \in I$ ，以及与该动作序列对应的时间序列 $T^{u} = (T_{1}^{u}, T_{2}^{u}, ..., T_{|T^{u}|}^{u})$ 。在训练过程中，在时间步t，模型根据前t个项目以及项目i和j之间的时间间隔 $r_{ij}^{u}$ 来预测下一个项目。我们模型的输入是 $(S_{1}^{u}, S_{2}^{u}, ..., S_{|S^{u}|-1}^{u})$ 以及序列中任意两个项目之间的时间间隔 $R^{u}$ ，其中 $R^{u} \in \mathbb{N}^{(|S^{u}|-1)\times ×(|S^{u}|-1)}$ 。我们期望的输出是每个时刻的下一个项目： $(S_{2}^{u}, S_{3}^{u}, ..., S_{|S^{u}|}^{u})$ 。

个性化时间间隔

我们将训练序列 $(S_{1}^{u}, S_{2}^{u}, \cdots, S_{|S^{u}| - 1}^{u})$ 转换为固定长度的序列 $\mathbf{s} = (s_1, s_2, \cdots, s_n)$ ，其中 n 表示我们所考虑的最大长度。如果序列长度大于 n，我们只考虑最近的 n 个动作。如果序列长度小于 n，我们在左侧填充占位项，直到长度达到 n。同样，对于时间序列 $T^{u} = (T_{1}^{u}, T_{2}^{u}, \cdots, T_{|T^{u}| - 1}^{u})$ ，我们也考虑一个固定长度的时间序列 $\mathbf{t} = (t_1, t_2, \cdots, t_n)$ 。如果时间序列长度小于 n，我们用第一个非填充项 $s_1$ 对应的时间戳 $T_{s_1}^{u}$ 进行填充。否则，我们只考虑前 n 个时间戳。

我们将交互序列中的时间间隔建模为两个物品之间的关系。有些用户的交互更频繁，而有些用户则不然，并且我们只关心单个用户序列中时间间隔的相对长度。因此，对于所有的时间间隔，我们将用户序列中（非零）最短的时间间隔作为除数，从而得到个性化的时间间隔。

【不同用户的交互频率不同，直接使用原始时间间隔不利于模型捕捉用户序列中时间间隔的相对重要性。】

给定用户 u 的固定长度时间序列 $\mathbf{t} = (t_1, t_2, \cdots, t_n)$ ，物品 i 和 j 之间的时间间隔为 $|t_i - t_j|$ ，用户 u 的时间间隔集合（不包括 0）为 $R^{u}$ 。我们将用户的最小时间间隔记为 $r_{\min}^{u}=\min(R^{u})$ 。缩放后的时间间隔为 $r_{ij}^{u}=\left\lfloor\frac{|t_i - t_j|}{r_{\min}^{u}}\right\rfloor$ ，其中 $r_{ij}^{u} \in \mathbb{N}$ 。因此，用户 u 的关系矩阵 $M^{u} \in \mathbb{N}^{n\times n}$ 为：

$M^{u}= \begin{bmatrix} r_{11}^{u} & r_{12}^{u} & \cdots & r_{1n}^{u} \\ r_{21}^{u} & r_{22}^{u} & \cdots & r_{2n}^{u} \\ \cdots & \cdots & \cdots & \cdots \\ r_{n1}^{u} & r_{n2}^{u} & \cdots & r_{nn}^{u} \end{bmatrix} \quad$

我们将所考虑的两个物品之间的最大相对时间间隔截断为 k。我们假设超过某个阈值后，精确的相对时间间隔就不再有用了。对最大时间间隔进行截断还可以避免关系编码过于稀疏，并使模型能够推广到训练过程中未见过的时间间隔。因此，截断后的矩阵为 $M_{\text{clipped}}^{u}=\text{clip}(M^{u})$ ，其中矩阵的截断操作应用于每个元素 $r_{ij}^{u}=\min(k, r_{ij}^{u})$ 。

【裁剪操作可以避免关系编码过于稀疏，因为过大的时间间隔可能导致编码的稀疏性增加，不利于模型学习。同时，裁剪也能使模型更好地推广到训练过程中未见过的时间间隔，增强模型的泛化能力，提高在不同数据集上的表现】

嵌入层

我们为物品创建一个嵌入矩阵 $M^I\in\mathbb{R}^{|I|\times d}$ ，其中d是潜在维度。用常数零向量 $\mathbf{0}$ 作为填充项的嵌入。嵌入查找操作会检索前n个物品的嵌入，并将它们堆叠在一起，得到一个矩阵 $E^I\in\mathbb{R}^{n\times d}$ ： $E^I = \begin{bmatrix} m_{s_1} \\ m_{s_2} \\ \vdots \\ m_{s_n} \end{bmatrix} \quad(3)$

我们分别使用两个不同的可学习位置嵌入矩阵 $M_K^P\in\mathbb{R}^{n\times d} M_V^P\in\mathbb{R}^{n\times d}$ ，用于自注意力机制中的键和值。这种方法更适合在自注意力机制中使用，无需额外的线性变换。检索后，我们得到嵌入 $E_K^P\in\mathbb{R}^{n\times d}$ 和 $E_V^P\in\mathbb{R}^{n\times d}$ ： $E_K^P = \begin{bmatrix} p_1^k \\ p_2^k \\ \vdots \\ p_n^k \end{bmatrix} \quad E_V^P = \begin{bmatrix} p_1^v \\ p_2^v \\ \vdots \\ p_n^v \end{bmatrix} \quad(4)$

与位置嵌入类似，相对时间间隔嵌入矩阵为 $M_K^R\in\mathbb{R}^{k\times d}$ 、 $M_V^R\in\mathbb{R}^{k\times d}$ ，用于自注意力中的键和值。在检索经过裁剪的关系矩阵 $M_{\text{clipped}}^u$ 后，我们得到嵌入矩阵 $E_K^R\in\mathbb{R}^{n\times n\times d}$ 和 $E_V^R\in\mathbb{R}^{n\times n\times d}$ ： $E_K^R = \begin{bmatrix} r_{11}^k & r_{12}^k & \cdots & r_{1n}^k \\ r_{21}^k & r_{22}^k & \cdots & r_{2n}^k \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1}^k & r_{n2}^k & \cdots & r_{nn}^k \end{bmatrix} \quad E_V^R = \begin{bmatrix} r_{11}^v & r_{12}^v & \cdots & r_{1n}^v \\ r_{21}^v & r_{22}^v & \cdots & r_{2n}^v \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1}^v & r_{n2}^v & \cdots & r_{nn}^v \end{bmatrix} \quad(5)$

这两个相对时间间隔嵌入矩阵是对称矩阵，主对角线上的元素均为零。

时间间隔感知自注意力机制

仅考虑时间间隔是不够的，因为用户交互序列中可能存在许多具有相同时间戳的情况。在这种情况下，模型将变成没有任何位置或关系信息的自注意力机制。因此，我们还考虑了序列中物品的位置。

时间间隔感知自注意力层对于由n个物品组成的每个输入序列 $E^{I} = (m_{s_1}, m_{s_2}, \cdots, m_{s_n})$ ，其中 $m_{s_i} \in \mathbb{R}^d$ ，计算一个新的序列 $Z = (z_1, z_2, \cdots, z_n)$ ，其中 $z_i \in \mathbb{R}^d$ 。每个输出元素 $z_i$ 是通过对线性变换后的输入元素以及关系/位置嵌入进行加权求和得到的： $z_i = \sum_{j=1}^{n} \alpha_{ij} \left( m_{s_j}W^V + r_{ij}^v + p_{j}^v \right)$ 其中 $W^V \in \mathbb{R}^{d \times d}$ 是用于值的输入投影。每个权重系数 $\alpha_{ij}$ 是使用softmax函数计算的： $\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{n} \exp(e_{ik})}$ 而 $e_{ij}$ 是使用一个考虑输入、关系和位置的兼容性函数计算的： $e_{ij} = \frac{m_{s_i}W^Q \left( m_{s_j}W^K + r_{ij}^k + p_{j}^k \right)^T}{\sqrt{d}}$ 其中 $W^Q \in \mathbb{R}^{d \times d}$ 、 $W^K \in \mathbb{R}^{d \times d}$ 分别是用于查询和键的输入投影。缩放因子 $\sqrt{d}$ 用于避免内积值过大，特别是在维度较高时。

因果性

由于序列的性质，模型在预测第(t + 1)个物品时，应该只考虑前t个物品。然而，时间感知自注意力层的第t个输出包含了所有的输入信息。因此，和[14]中一样，我们通过禁止 $Q_i$ 和 $K_j$ ( j > i)之间的所有连接来修改注意力，其中 $Q_i = m_{s_i}W^Q, K_j = m_{s_j}W^K + r_{ij}^k + p_{j}^k$ 。

逐点前馈网络

尽管我们的时间间隔感知注意力层能够通过自适应权重整合所有先前物品、绝对位置和相对时间信息，但它是通过线性组合实现的。在每个时间感知注意力层之后，我们应用两个线性变换，并在中间使用ReLU激活函数，这可以为模型赋予非线性特性： $\text{FFN}(z_i) = \max(0, z_iW_1 + b_1)W_2 + b_2$ 其中 $W_1, W_2 \in \mathbb{R}^{d \times d}$ ， $b_1, b_2 \in \mathbb{R}^d$ 。虽然不同物品的线性变换是相同的，但不同层使用不同的参数。正如[14]中所讨论的，堆叠自注意力层和前馈层后，会出现更多问题，包括过拟合、训练过程不稳定（例如梯度消失）以及需要更多的训练时间。和[26]、[14]一样，我们也采用层归一化、残差连接和随机失活正则化技术来解决这些问题： $Z_i = z_i + \text{Dropout}(\text{FFN}(\text{LayerNorm}(z_i)))$ 层归一化用于对输入特征进行归一化（即零均值和单位方差）。根据[1]，这可以稳定并加速神经网络的训练。假设x是一个包含样本所有特征的向量，层归一化定义为： $\text{LayerNorm}(x) = \alpha \odot \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta$ 其中 $\odot$ 是逐元素乘积， $\mu$ 和 $\sigma$ 是x的均值和方差， $\alpha$ 和 $\beta$ 是学习到的缩放因子和偏差项。

模型推理

回顾一下，我们将物品序列 $(S_{1}^{u}, S_{2}^{u}, \cdots, S_{|S^{u}| - 1}^{u})$ 和时间序列 $T^{u} = (T_{1}^{u}, T_{2}^{u}, \cdots, T_{|T^{u}| - 1}^{u})$ 分别转换为固定长度的序列 $\mathbf{s} = (s_1, s_2, \cdots, s_n)$ 和 $\mathbf{t} = (t_1, t_2, \cdots, t_n)$ 。我们将 $\mathbf{o} = (o_1, o_2, \cdots, o_n)$ 定义为给定时间和物品序列的预期输出。 $\mathbf{o}$ 中的元素 $o_i$ 定义如下：

其中， $<\text{pad}>$ 表示填充项。

由于用户交互数据是隐式数据，我们无法直接优化偏好得分 $R_{i,t}$ 。我们模型的目标是提供一个物品排序列表。因此，我们采用负采样来优化物品的排序。对于每个预期的正输出 $o_i$ ，我们从不属于 $S^{u}$ 的物品中采样一个负样本 $o_i'$ ，生成一组成对的偏好序 $D = \{(S^{u}, T^{u}, \mathbf{o}, \mathbf{o}')\}$ 。我们使用sigmoid函数 $\sigma(x) = 1 / (1 + e^{-x})$ 将模型输出分数转换到$(0, 1)$区间，并采用二元交叉熵作为损失函数： $-\sum_{S^{u} \in S}\sum_{t \in [1, 2, \cdots, n]} \left[ \log(\sigma(r_{o_t,t})) + \log(1 - \sigma(r_{o_t',t})) \right] + \lambda \|\Theta\|_F^2 \quad(14)$ 其中， $\Theta = \{M^{I}, M_{K}^{P}, M_{V}^{P}, M_{K}^{R}, M_{V}^{R}\}$ 是嵌入矩阵的集合， $\|\cdot\|_F$ 表示Frobenius范数， $\lambda$ 是正则化参数。注意，我们会屏蔽填充项的损失。所提出的模型使用Adam优化器[15]进行优化。由于每个训练样本 $D = \{(S^{u}, T^{u}, \mathbf{o}, \mathbf{o}')\}$ 都可以独立构建，我们采用小批量随机梯度下降（mini - batch SGD）来提高训练效率。