Python机器学习---5.决策树
决策树概念:决策树是⼀种树形结构,通过特征的不同来将样本数据划分到不同的分⽀(⼦树)中,最终,每个样本 ⼀定会划分到⼀个叶⼦节点中。我们可以将每个特征视为⼀个问题(提问), 特征值的不同,就视为样本给出的不同答案,然后,我们就可以根据⼀系列问题(特征), 将样本划分到不同的叶⼦节点中。决策树可以⽤于分类与回归任务。
决策树的介绍: 决策树学习采⽤的是⾃顶向下的递归⽅法,其基本思想是以信息熵为度量构造⼀棵熵值,下降最快的树,到叶⼦节点处的熵值为零,此时每个叶节点中的实例都属于同⼀类。
决策树特征选择:
-
信息熵:决策树的信息熵是⽤来度量样本集合纯度的指标。信息熵越⼤,表示样本集合的不确定性越⼤;信息熵越⼩,表示样本集合的确定性越⾼。在决策树的构建过程中,信息熵被⽤来作为划分属性的依据,通过计算不同属性划分后的信息熵来选择最优划分属性,以使得整个决策树的熵值最⼩,从⽽使得整个决策系统的确定性最⾼。
-
计算⽅式:假设随机变量具有个值,分别为:V1,V2 ,V3... ,Vm。并且各个值出现的概率如下:

-
不纯度:决策树的不纯度是指落在当前节点的样本类别分布的均衡程度。如果类别⼀致,那么不纯度为0,叶⼦节点和是相对纯的。在决策树的每个叶⼦节点中都会包含⼀组数据,这组数据中,如果某⼀类标签占有较⼤的⽐例,我们就说叶⼦节点“纯”,分枝分得好。某⼀类标签占的⽐例越⼤,叶⼦就越纯,不纯度就越低,分枝就越好。如果没有哪⼀类标签的⽐例很⼤,各类标签都相对平均,则说叶⼦节点”不纯“,分枝不好,不纯度⾼。不纯度是决策树算法中⼀个重要的概念,它可以帮助我们判断在每个节点处进⾏分裂是否合适。⼀般来说,不纯度越低,说明数据在该节点处越能被分裂得均匀,该节点的分裂效果越好。因此,决策树算法会选择不纯度下降最⼤的地⽅进⾏分裂。
-
信息增益:
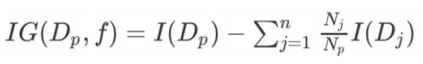
-
f:划分的特征。
-
Dp: ⽗节点,即使⽤特征f分割之前的节点。
-
IG(Dp,f): ⽗节点Dp使⽤特征f划分下,获得的信息增益。
-
Dj: ⽗节点Dp经过分割之后,会产⽣n个⼦节点, Dj为第j个⼦节点。
-
Np: ⽗节点 Dp包含样本的数量。
-
Nj: 第 j个⼦节点Dj包含样本的数量。
-
I: 不纯度度量标准。例如,之前介绍的信息熵,就是标准之⼀。后⾯公式就是⽤信息熵H。
-
出于简化与缩⼩组合搜索空间的考虑,很多库(包括scikit-learn)实现的都是⼆叉决策树,即每个⽗节点最多含有两个⼦节点(左⼦树节点与右⼦树节点),此时信息增益定义为: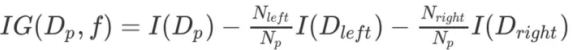
不纯度度量标准:不纯度可以采⽤如下⽅式度量
-
信息熵(Entropy):
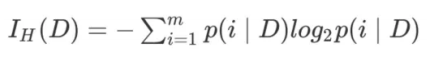
-
m: 节点D中含有样本的类别数量。
-
P(i|D): 节点D中,属于类别i 的样本占节点 D中样本总数的⽐例(概率)。
-
-
基尼系数(Gini Index):
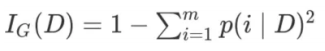
-
错误率(classification error):
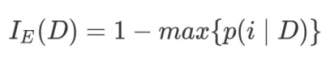
决策树算法:决策树主要包含以下三种算法
-
ID3 Iterative Dichotomiser:ID3 即信息增益,ID3(Iterative Dichotomiser3-迭代⼆分法)算法是⾮常经典的决策树算法,该算法描述如下:
-
使⽤多叉树结构。
-
使⽤信息熵作为不纯度度量标准,选择信息增益最⼤的特征分割数据。
-
-
C4.5:C4.5算法是在ID3算法上改进⽽来,该算法描述如下:
-
使⽤多叉树结构。
-
仅⽀持分类,不⽀持回归。
不过,C4.5在ID3算法上,进⾏了⼀些优化,包括:-
⽀持对缺失值的处理。
-
⽀持将连续值进⾏离散化处理。
-
使⽤信息熵作为不纯度度量标准,但选择信息增益率(⽽不是信息增益)最⼤
的特征分裂节点。
-
-
信息增益率的定义⽅式为:

-
-
CART(Classification And Regression Tree):分类与回归树。该算法描述如下:
-
使⽤⼆叉树结构。
-
⽀持连续值与缺失值处理。
-
既⽀持分类,也⽀持回归。
-
使⽤基尼系数作为不纯度度量标准,选择基尼增益最⼤的特征分裂节点。(分类)
-
使⽤MSE或MAE最⼩的特征分类节点。(回归)
-
-
回归决策树:当使⽤回归决策树时,与分类决策树会有所不同。回归任务的标签( 值)是连续的,故之前以分类为基础的不纯度度量标准(信息熵,基尼系数与错误率)都不适⽤于回归树,因此,在回归树中,⾃然也就没有信息增益,信息增益率或基尼增益等概念了。可以说,分类决策树选择特征的⽅式,完全不适⽤于回归决策树。
分类决策树:
# 读取数据,划分特征列和目标列
X, y = load_iris(return_X_y=True)
X = X[:, :2]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, random_state=1)# 实例化,并且设置最大深度
tree = DecisionTreeClassifier(max_depth=5)# 拟合
tree.fit(X_train, y_train)# 预测
Y = tree.predict(X_test)# print(Y)
# print("训练集:", tree.score(X_train, y_train))
# print("测试集:", tree.score(X_test, y_test))
# print("分析报告:", classification_report(y_test, Y))肘部法则:
# 肘部法则,找到决策树的最合适的最大深度
# train_score = []
# test_score = []
# for depth in range(1, 13):
# tree = DecisionTreeClassifier(random_state=0, max_depth=depth)
# tree.fit(X_train, y_train)
# train_score.append(tree.score(X_train, y_train))
# test_score.append(tree.score(X_test, y_test))
# plt.figure(figsize=(10, 5))
# plt.plot(train_score, marker='o', c='red', label='训练集')
# plt.plot(test_score, marker='o', c='green', label='测试集')
# plt.legend()
# plt.show()回归决策树:
# 读取数据
data = pd.read_csv(r'boston.csv')# 划分特征列和目标列
X = data.iloc[:, : -1]
y = data.iloc[:, -1]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.75, random_state=1)# 实例
tree = DecisionTreeRegressor(max_depth=4)# 拟合
tree.fit(X_train, y_train)print("训练集:", tree.score(X_train, y_train))
print("测试集:", tree.score(X_test, y_test))# # 肘部法则
# train_score = []
# test_score = []
# for depth in range(1, 10):
# tree1 = DecisionTreeRegressor(random_state=0, max_depth=depth)
# tree1.fit(X_train, y_train)
# train_score.append(tree1.score(X_train, y_train))
# test_score.append(tree1.score(X_test, y_test))
# plt.figure(figsize=(10, 5))
# plt.plot(train_score, marker='o', c='red', label='训练集')
# plt.plot(test_score, marker='o', c='green', label='测试集')
# plt.legend()
# plt.show()