数据结构3：复杂度

目录

前言：

一、时间复杂度

二、大O的渐进表示法

2.1练习一

2.2练习2

2.3练习3

2.4练习4

2.5练习5

2.6练习6

2.7练习7

2.8练习8

三、空间复杂度

3.1练习1

3.2练习2

3.3练习3

总结

---

前言：

当我们学习到现在的程度时，在一些编写代码的场合我们不得不考虑一个问题，在编写成可执行程序后，运行时需要耗费时间资源和空间(内存)资源。因此我们在编写程序的时候就需要注意算法的复杂度，衡量一个算法的好坏，一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。时间复杂度主要衡量一个算法的运行快慢，而空间复杂度主要衡量一个算法运行所需要的额外空间。在以前计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。

一、时间复杂度

算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。一个算法执行所耗费的时间，从理论上说，这是不能算出来的，只有你把你的程序放在机器上跑起来，才能知道。但是我们需要每个算法都上机测试吗？这是不太可能的一是太过于麻烦二是我们的计算机性能都不一样，所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

就比如下面的代码，请计算一下Func1执行了多少次？

void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++j){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

我们理解一下就可以计算出应该是N*N+2*N+10次，但如果N=10时，结果未为130，N=100时，结果为100210，N=1000时，结果为1002010.我们可以观察到当N越大时常数项对结果的影响越小。实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，（上述同样的道理其实我们刚刚计算结果时像++count，printf等我们应该也算上次数中，但也是因为不一定要精确计算所以就忽略了）那么这里我们使用大O的渐进表示法。

我们可以通过一些代码来感受时间复杂度

int main()
{//计算从程序启动到调用该函数的毫秒数int beginn1 = clock();int n = 100000000;int i = 0;int x = 10;for (i = 0; i < n; i++){++x;}int end1 = clock();printf("%d\n", x);printf("%d\n", end1 - beginn1);return 0;
}

二、大O的渐进表示法

大O符号：是用于描述函数渐进行为的数学符号。

推导大O阶方法：

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

下图是一张大O常见量级的表格图片

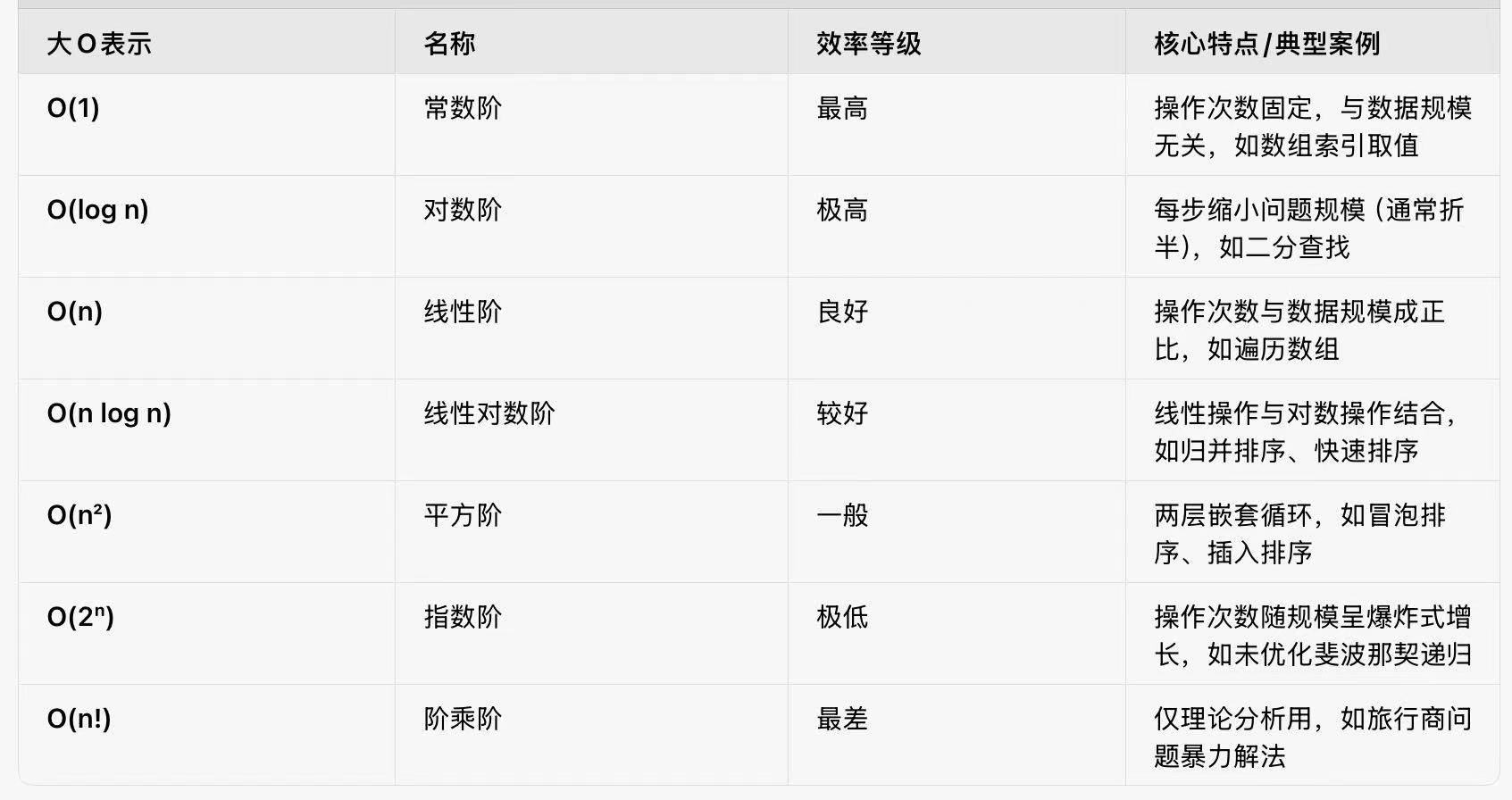
提高一个量级带来的时间复杂度的增加是高很多倍的，我们也可以用代码来感受一下

int main()
{int x = 0;int begin1 = clock();for (int i = 0; i < 100000; i++){for (int i = 0; i < 100000; i++){++x;}}int end1 = clock();printf("%d\n", x);printf("%d\n", end1 - begin1);return 0;
}

接下来我们用几个练习题，来理解一下概念

2.1练习一

void Func(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}

基本操作执行了2N+10次，通过推导大O阶方法知道，时间复杂度为 O(N)，2也要去掉是因为在大到一定程度1和2没有太大差距。

2.2练习2

void Func(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}

基本操作执行了M + N次，有两个未知数M和N，时间复杂度为 O(N + M)如果M>>N,0(M)，如果N>>M,O(N)

2.3练习3

void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}

基本操作执行了100次，通过推导大O阶方法，时间复杂度为 O(1)
O（1）不是代表一次而是代表常数次

2.4练习4

const char* strchr(const char* str, int character);

这个代码的意思是在一个字符串里查找字符在一个字符串里查找字符在一个字符串里查找字符。

基本操作执行最好1次，最坏N次，时间复杂度一般看最坏，所以时间复杂度为 O(N)

2.5练习5

void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

这是一个冒泡排序，基本操作执行最好N次，最坏执行了(N* (N + 1) / 2次，通过推导大O阶方法  时间复杂度一般看最坏，时间复杂度为 O(N ^ 2)

2.6练习6

void func(int n)
{int x = 0;for (int i = 0; i < n; i *= 2){++x;}printf("%d\n", x);
}

基本操作执行最好1次，最坏O(logN)次，时间复杂度为 O(logN) ps：logN在算法分析中表示是底

数为2，对数为N。有些地方会写成lgN。 

2.7练习7

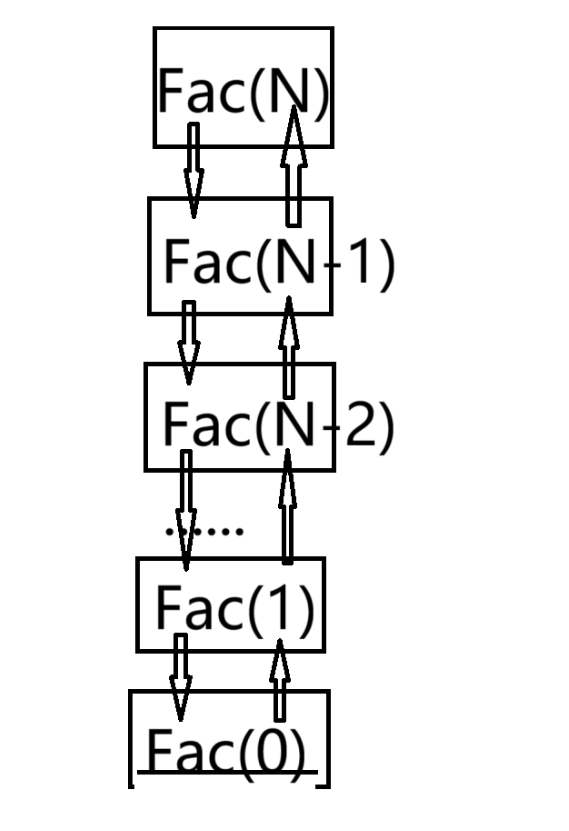
// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}

通过计算分析发现基本操作递归了N次，时间复杂度为O(N)。

递归如果不够理解可以去看一下我之前的递归函数的博客（链接：https://blog.csdn.net/chen060603/article/details/151186171?spm=1001.2014.3001.5501）

要注意我们这里时间复杂度不是O（N*N）

从N到0一共Fac调用了N+1次。

2.8练习8

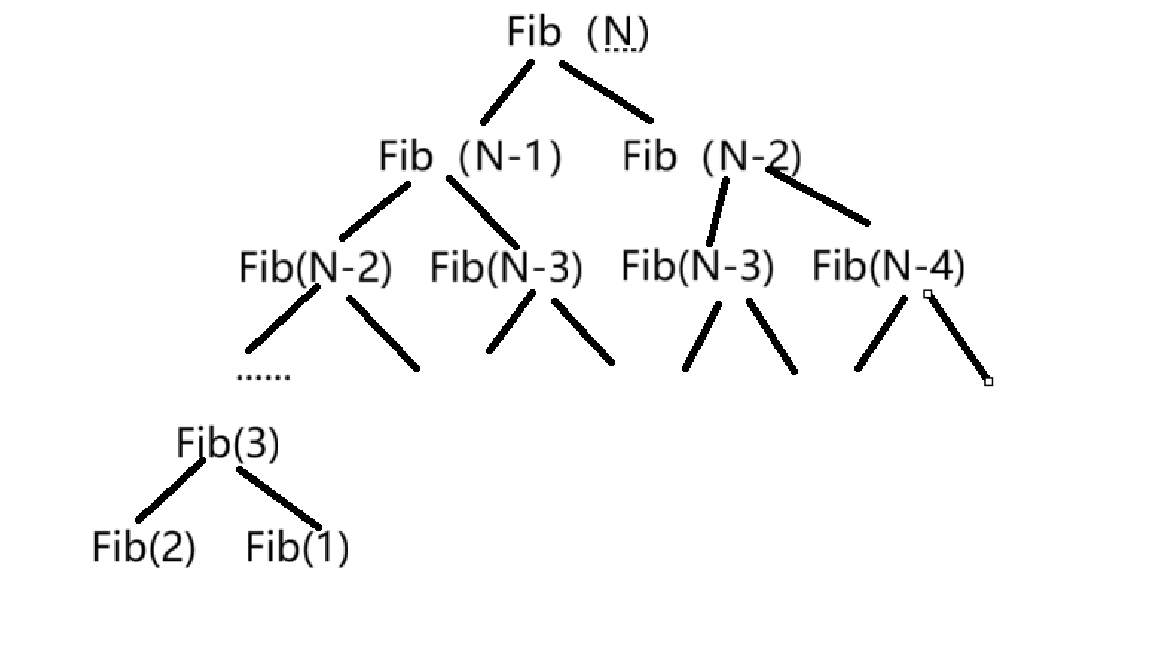
// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}

通过计算分析发现基本操作递归了2^N次，时间复杂度为O(2^N)。

这种写法的斐波那契递归的时间复杂度比较高。如果感兴趣的话可以试一试递归50次看一下所需要的时间。

这个斐波那契递归的思路图如下，所以他的次数计算是2^0+2^1+2^2+......+2^(N-2)，后面利用数学公式求解即可。

三、空间复杂度

空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。

空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似，也使用大O渐进表示法。

注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。

我们也可以举几个例子来帮助理解

3.1练习1

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}

使用了常数个额外空间，所以空间复杂度为 O(1)

3.2练习2

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}

动态开辟了N个空间，空间复杂度为 O(N)

3.3练习3

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}

递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

总结

时间复杂度用O() 表示算法执行时间随输入规模的增长趋势，核心看“最耗时操作的次数”，常见效率排序：O(1)＞O(log n)＞O(n)＞O(n log n)＞O(n²)＞O(2ⁿ)。

空间复杂度用O() 表示算法额外内存占用随输入规模的增长趋势，核心看“额外变量/结构的占用”，常见类型：O(1)（常数空间）、O(n)（线性空间）、O(n²)（平方空间）。

两者均忽略常数项和低次项，重点反映算法的“ scalability（可扩展性）”，多数场景优先用“空间换时间”优化。

后续我会继续更新关于这些方面的算法题希望帮助大家更好理解，期待我们共同进步。