当前位置：首页 > news >正文

有限元方法核心原理与学习路径：从一维基础到多维拓展（七步流程）

news 2025/10/24 7:53:41

🌟 有限元学习七步流程（系统优化版）

① 理论入门：掌握物理本质

建立力学三大基本关系（以一维杆为例）：

平衡方程：
$dσdx+f=0\frac{d\sigma}{dx} + f = 0$
几何关系：
$ε=dudx\varepsilon = \frac{du}{dx}$
本构关系：
$σ=Eε\sigma = E\,\varepsilon$

材料假设： 线性弹性、均质、各向同性。
目标： 明确应力–应变–位移之间的物理因果关系。

② 数学建模：位移与应变的假设

假设线性位移场：
$c\,x$
边界条件：
$u (0) = 0$
根据力平衡和边界条件：
$\frac{P}{E A}$
因此：
$ε=dudx=PEA,σ=Eε=PA\varepsilon = \frac{du}{dx} = \frac{P}{E A}, \quad \sigma = E\varepsilon = \frac{P}{A}$

③ 能量法与虚功原理：建立变分关系

采用势能极值原理：
$Π(u)=U−W\Pi(u) = U - W$

平衡条件由：
$δΠ=0⇒δU=δW\delta \Pi = 0 \quad \Rightarrow \quad \delta U = \delta W$

对于杆件问题：
$\frac{P}{E A}x, \quad \varepsilon = \frac{P}{E A}, \quad \sigma = \frac{P}{A}$

⚙️ 虚功原理推导过程

(1) 虚功方程

$δU=δW\delta U = \delta W$

(2) 应变能变化

$δW=P(x)δu(x)\delta W = P(x)\,\delta u(x)$

$δU=δ(12∫Ωσ(x)ε(x)dV)\delta U = \delta \left( \frac{1}{2} \int_{\Omega} \sigma(x)\,\varepsilon(x)\, dV \right)$

(3) 试函数

$c\,x \quad \Rightarrow \quad \delta u(x) = \delta c \cdot x$

$σ(x)=Eε(x)⇒δσ(x)=E⋅δc\sigma(x) = E\,\varepsilon(x) \quad \Rightarrow \quad \delta\sigma(x) = E \cdot \delta c$

$ε(x)=dudx⇒δε(x)=δc\varepsilon(x) = \frac{du}{dx} \quad \Rightarrow \quad \delta\varepsilon(x) = \delta c$

(4) 应变能变化计算

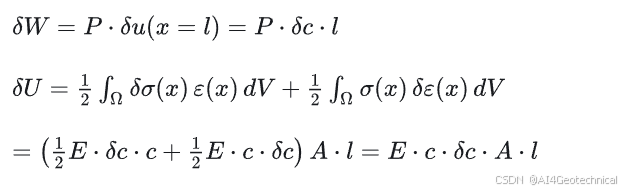
在这里插入图片描述

(5) 平衡结果

$\frac{P}{E A}, \quad \varepsilon(x) = \frac{P}{E A}, \quad \sigma(x) = \frac{P}{A}, \quad u(x) = \frac{P}{E A}x$

⚙️ 最小势能原理推导

(1) 最小势能原理

$min⁡u(x)∈BC(u)[Π(u)=U−W]\min_{u(x) \in BC(u)} \big[\, \Pi(u) = U - W \,\big]$

(2) 系统应变能

$\frac{1}{2} \int_{\Omega} \sigma(x)\,\varepsilon(x)\, dV$

(3) 系统外力势能

$\cdot u(x = l)$

(4) 势能函数

$Π(u)=12Ec2Al−Pcl\Pi(u) = \frac{1}{2} E\, c^2\, A\, l - P\, c\, l$

(5) 取极值条件

$∂Π∂c=0\frac{\partial \Pi}{\partial c} = 0$

(6) 试函数与结果

$c\,x, \quad \varepsilon(x) = c, \quad c = \frac{P}{E A}$

同样得到：
$ε(x)=PEA,σ(x)=PA,u(x)=PEAx\varepsilon(x) = \frac{P}{E A}, \quad \sigma(x) = \frac{P}{A}, \quad u(x) = \frac{P}{E A}\, x$

④ 弱形式与有限元基础

由强形式（微分方程）通过分部积分得到弱形式：
$∫0LEAdudxdvdxdx=∫0Lfvdx+[Tˉv]L\int_0^L EA \frac{du}{dx}\frac{dv}{dx}dx = \int_0^L f\,v\,dx + [\bar{T}v]_L$

边界条件：

本质边界条件：直接作用于位移，如 $u (0) = 0$ ；
自然边界条件：由弱式自动包含，如 $σ(L)=Tˉ\sigma(L) = \bar{T}$ 。

⑤ 有限元离散与矩阵方程

单元内位移近似：
$u(ξ)=N1u1+N2u2,N1=1−ξ,N2=ξu(\xi) = N_1 u_1 + N_2 u_2, \quad N_1 = 1 - \xi, \; N_2 = \xi$
单元刚度矩阵：
$Ke=∫0LBTEABdx=EAL[1−1−11]K_e = \int_0^L B^T E A B\,dx = \frac{E A}{L} \begin{bmatrix} 1 & -1 \\ -1 & 1 \end{bmatrix}$
全局组装： 按节点连接关系叠加 $K_e$ 形成整体刚度矩阵 $K$ 。

⑥ 数值计算与验证

通过求解线性方程：
$K U = F$
得到节点位移。
计算应变与应力：
$ε=BUe,σ=Eε\varepsilon = B U_e, \quad \sigma = E \varepsilon$
与解析解对比，验证有限元解的正确性。

⑦ 知识融合与高维扩展

（1）从一维到二维的推广

二维问题常见于平面应力与平面应变状态：

$\quad v = v(x, y)$

几何方程（应变–位移关系）：
$εx=∂u∂x,εy=∂v∂y,γxy=∂u∂y+∂v∂x\begin{aligned} \varepsilon_x &= \frac{\partial u}{\partial x}, \\ \varepsilon_y &= \frac{\partial v}{\partial y}, \\ \gamma_{xy} &= \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \end{aligned}$

矩阵形式：

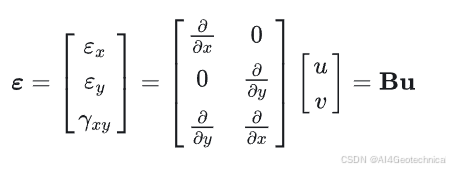
在这里插入图片描述

平面应力本构关系：
$Dplane-stress=E1−ν2[1ν0ν10001−ν2]\mathbf{D}_{\text{plane-stress}} = \frac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & \frac{1-\nu}{2} \end{bmatrix}$

平面应变本构关系：
$Dplane-strain=E(1−ν)(1+ν)(1−2ν)[1ν1−ν0ν1−ν10001−2ν2(1−ν)]\mathbf{D}_{\text{plane-strain}} = \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 & \frac{\nu}{1-\nu} & 0 \\ \frac{\nu}{1-\nu} & 1 & 0 \\ 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{bmatrix}$

二维单元刚度矩阵：
$Ke=∫VBTDBdV\mathbf{K}_e = \int_V \mathbf{B}^T \mathbf{D} \mathbf{B}\, dV$

（2）三维问题的拓展

三维位移场：
$\quad v = v(x,y,z), \quad w = w(x,y,z)$

应变分量：
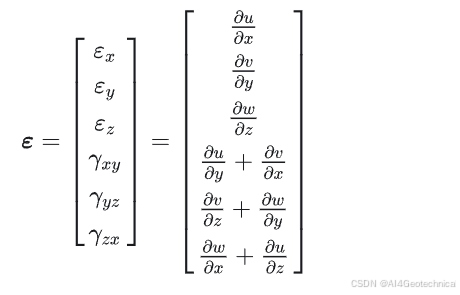
在这里插入图片描述

三维线弹性本构矩阵：
$D3D=E(1−ν)(1+ν)(1−2ν)[1ν1−νν1−ν000ν1−ν1ν1−ν000ν1−νν1−ν10000001−2ν2(1−ν)0000001−2ν2(1−ν)0000001−2ν2(1−ν)]\mathbf{D}_{3D} = \frac{E(1-\nu)}{(1+\nu)(1-2\nu)} \begin{bmatrix} 1 & \frac{\nu}{1-\nu} & \frac{\nu}{1-\nu} & 0 & 0 & 0 \\ \frac{\nu}{1-\nu} & 1 & \frac{\nu}{1-\nu} & 0 & 0 & 0 \\ \frac{\nu}{1-\nu} & \frac{\nu}{1-\nu} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1-2\nu}{2(1-\nu)} \end{bmatrix}$