P4766 [CERC2014] Outer space invaders 题解

P4766 [CERC2014] Outer space invaders

$n$ 个外星人要杀你，第 $i$ 个在 $a_i$ 出现，距离你 $d_i$,必须在 $b_i$ 及以前被消灭，炮可以每次花费 $w$ 的代价销毁距离在 $w$ 及以内的所有外星人，问消灭所有外星人的最低成本。$n\le 300,a_i,b_i,d_i\le 10000$

每次发射肯定是瞄准最远的那个，那么所有出现时间跨过此时的外星人都被消灭。外星人出现区间便分成了完全不交的两部分。
如图：

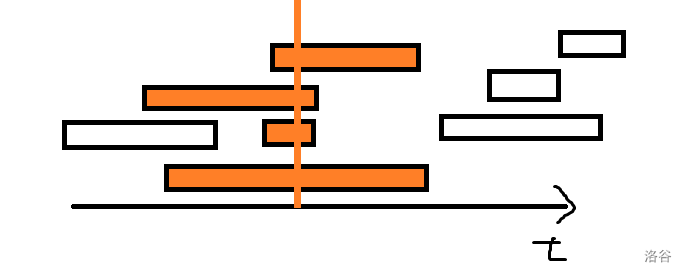
我们设 $f_{l,r}$ 表示消灭出现时间区间都在 $l,r$ 之间的机器人最小花费。
又因为每次肯定瞄准能瞄准的中最远的那个，所有设 $pi$ 为最远的那个。
柿子为：
$f_{l,r}=\min (f_{l,k-1}+f_{k+1,r}+p{i}_w)$
记得离散化。

code:

```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=605;
const int INF=0x3f3f3f3f;
int T,n;
int f[N][N]; 
int L[N],R[N];
struct node{int l,r,w;
}a[N];
int main(){scanf("%d",&T);while(T--){int mx=-INF;scanf("%d",&n);int nn=0;for(int i=1;i<=n;i++){scanf("%d%d%d",&a[i].l,&a[i].r,&a[i].w);L[++nn]=a[i].l;L[++nn]=a[i].r;}sort(L+1,L+1+nn);int li=unique(L+1,L+1+nn)-L-1;for(int i=1;i<=n;i++){a[i].l=lower_bound(L+1,L+1+li,a[i].l)-L;a[i].r=lower_bound(L+1,L+1+li,a[i].r)-L;mx=max(mx,a[i].r);//	cout<<a[i].l<<" "<<a[i].r<<endl;}for(int le=1;le<=mx;le++){for(int l=1;l+le-1<=mx;l++){int r=l+le-1;int p=0,pi=0;for(int i=1;i<=n;i++){if(a[i].l>=l&&a[i].r<=r&&a[i].w>p){p=a[i].w,pi=i;}} if(p==0) {f[l][r]=0;continue;}f[l][r]=INF;for(int k=a[pi].l;k<=a[pi].r;k++){f[l][r]=min(f[l][r],f[l][k-1]+f[k+1][r]+p);}//	cout<<l<<" "<<r<<" "<<f[l][r]<<endl;}}//	cout<<mx<<endl;printf("%d\n",f[1][mx]);}return 0;
}