基于频率分集阵列的MIMO雷达联合距离角度估计——论文阅读

基于频率分集阵列的MIMO雷达联合距离角度估计

J. Xu, G. Liao, S. Zhu, L. Huang and H. C. So, “Joint Range and Angle Estimation Using MIMO Radar With Frequency Diverse Array,” in IEEE Transactions on Signal Processing, vol. 63, no. 13, pp. 3396-3410, July1, 2015

1. 引言

多输入多输出（MIMO）雷达作为一种灵活的技术，在不牺牲相控阵雷达优势的同时享有诸多优点，近年来受到了广泛关注。与传统相控阵雷达不同，MIMO雷达能够通过发射正交波形在时域和利用发射接收天线阵列结构在空域有效利用自由度（DOFs），这最终导致了可识别性和分辨率的显著提升。

传统相控阵雷达的一个关键限制是其波束方向对所有距离都是固定的，因此，当存在固有距离模糊时，目标的距离无法从波束形成输出中直接估计。虽然增加脉冲重复频率（PRF）可以实现更高水平的杂波抑制并消除多普勒模糊，但PRF的增加可能导致最大无模糊距离远小于期望的工作距离。

频率分集阵列（FDA）首次由Antonik等人在2006年提出，作为一种灵活的波束扫描阵，FDA与传统相控阵最重要的区别在于，波形的载波频率在阵列单元间以小量递增。由于每个FDA单元辐射相干波形，因此获得了依赖于距离-角度-时间的波束方向图。这种连续波束扫描特性已通过仿真示例进行了评估，并从设计角度进行了研究。

本文提出的方法利用了FDA-MIMO雷达的距离角度依赖特性，提出了一种无模糊的距离角度估计方法。由于发射导向矢量依赖于距离和角度参数，FDA-MIMO雷达可以在联合距离角度维度引入可控的发射自由度。

2. 同址FDA-MIMO雷达信号模型

2.1 系统配置与信号模型

考虑一个同址MIMO雷达系统，由$N$个发射天线和$M$个接收天线组成。第$n$个天线的载波频率为：

$$f_n=f_0+(n-1)\Delta f,n=1,2,\dots ,N$$

其中$\Delta f$是阵列单元间的频率增量，$f_0$是参考载波频率。频率增量相对于载波频率和发射波形带宽可以忽略不计。

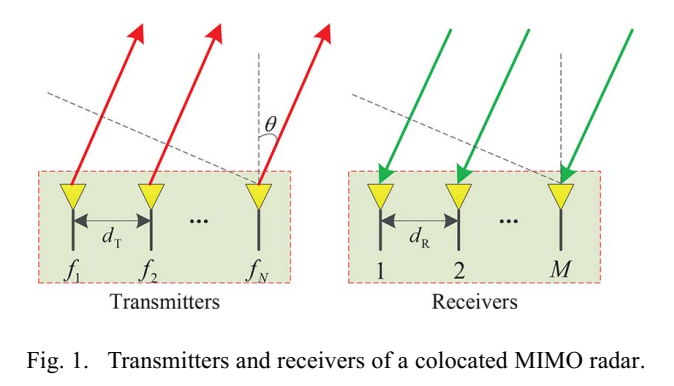
图1描述：图1展示了同址MIMO雷达的发射机和接收机配置。发射阵列和接收阵列均匀排列，发射天线间距为$d_T$，接收天线间距为$d_R$。坐标系原点选在第一个发射天线处。

第$n$个单元的发射信号可以表示为：

$$s_n(t)=\sqrt{\frac{E}{N}}{\varphi }_n(t)e^{j2\pi f_{n}t},0\le t\le T,n=1,2,\dots ,N$$

其中$E$是总发射能量，$T$是雷达脉冲持续时间，${\varphi }_n(t)$表示单位能量波形，即${\int }_T|{\varphi }_n(t){|}^{2}dt=1$。假设波形满足正交条件：

$${\int }_T{\varphi }_m(t){\varphi }_n^{\ast }(t-\tau )e^{j2\pi \Delta f(m-n)t}dt=0,m\ne n,\forall \tau$$

2.2 接收信号模型

假设电磁波在自由空间独立传播。对于双向传播情况，选择第一个单元作为参考点。因此，对于任意目标，第$m$个单元的接收回波可以写为：

$$y_m(t)=\sum _{n=1}^N\left\{\sqrt{\frac{E}{N}}\xi {\varphi }_n(t-{\tau }_{n,T}-{\tau }_{m,R})\times e^{j2\pi (f_n+f_{d,n})(t-{\tau }_{n,T}-{\tau }_{m,R})}\right\}$$

其中$\xi$是目标的复值反射系数，$f_{d,n}$表示多普勒频率，即$f_{d,n}=2v_t{f}_n/c$，$v_t$是目标的径向速度，${\lambda }_n=c/f_n$是对应第$n$个发射天线的波长。

发射和接收时延分别为：

$${\tau }_{n,T}=\frac{1}{c}[r-d_T(n-1)\sin (\theta )]=\frac{r_0}{2}-\frac{d_T}{c}(n-1)\sin (\theta )$$

$${\tau }_{m,R}=\frac{1}{c}[r-d_R(m-1)\sin (\theta )]=\frac{r_0}{2}-\frac{d_R}{c}(m-1)\sin (\theta )$$

其中$\theta$表示目标角度（从法线方向到目标方向测量），$r$是目标距离，$d_T$和$d_R$分别是发射和接收天线间距。

2.3 匹配滤波与虚拟数据快照

在接收阵列中，测量信号被下变频、匹配滤波并存储，接收信号可以通过匹配滤波器分解，产生隔离的发射信号。匹配滤波器表达式为$h_n(t)={\varphi }_n^{\ast }(T-t)e^{-j2\pi f_n(T-t)}$。

经过匹配滤波后，第$m$个接收天线的第$n$个输出为：

$$z_{m,n}\approx \xi e^{j2\pi (f_0+f_d)T}{e}^{-j2\pi [\frac{d_T}{{\lambda }_0}(n-1)+\frac{2\Delta f}{c}(n-1)r]\sin \theta }{e}^{-j2\pi \frac{d_R}{{\lambda }_0}(m-1)\sin \theta }$$

第$m$个单元的输出可以写成矢量形式：

$${\mathbf{y}}_m=[z_{m,1},z_{m,2},\dots ,z_{m,N}{]}^T$$

因此，目标信号的虚拟数据快照可以表示为：

$$\mathbf{y}=\xi \mathbf{b}(\theta )\otimes \mathbf{a}(r,\theta )$$

其中$\otimes$表示Kronecker积，$\mathbf{a}(r,\theta )$和$\mathbf{b}(\theta )$分别是发射和接收导向矢量。

3. 发射导向矢量的距离角度依赖性分析

3.1 导向矢量的结构

发射和接收导向矢量定义为：

$$\mathbf{a}(r,\theta )=[1,e^{-j{\psi }_2},\dots ,e^{-j{\psi }_N}{]}^T$$

$$\mathbf{b}(\theta )=[1,e^{-j{\phi }_2},\dots ,e^{-j{\phi }_M}{]}^T$$

其中：

$${\psi }_n=2\pi \left(\frac{d_T}{{\lambda }_0}\sin \theta +\frac{2\Delta f}{c}r\right)(n-1)$$

$${\phi }_m=2\pi \frac{d_R}{{\lambda }_0}(m-1)\sin \theta$$

从上述公式可以看出，FDA-MIMO雷达的发射导向矢量不仅是角度依赖的，还是距离依赖的：

$$\mathbf{a}(r,\theta )={\mathbf{a}}_r(r)\odot {\mathbf{a}}_{\theta }(\theta )$$

其中$\odot$是Hadamard（逐元素）积，${\mathbf{a}}_r(r)$是发射距离导向矢量，${\mathbf{a}}_{\theta }(\theta )$是发射角度导向矢量。

3.2 干扰和噪声模型

假设有$L$个干扰信号从方向{θl}l=1L\{\theta_l\}_{l=1}^L{θl​}l=1L​入射到阵列。接收的干扰可以表示为：

$$\mathbf{j}=\sum _{l=1}^L{\beta }_l\mathbf{b}({\theta }_l)\otimes {\tilde{\mathbf{a}}}_l$$

其中${\beta }_l$是零均值圆对称复高斯随机变量，方差为${\sigma }_{J_l}^2$，即${\beta }_l\sim \mathcal{C}\mathcal{N}(0,{\sigma }_{J_l}^2)$。${\tilde{\mathbf{a}}}_l$是对应的类噪声发射导向矢量。

干扰的协方差矩阵可以计算为：

J=E{jjH}=∑l=1LσJl2b(θl)bH(θl)⊗IN\mathbf{J} = E\{\mathbf{j}\mathbf{j}^H\} = \sum_{l=1}^{L} \sigma_{J_l}^2 \mathbf{b}(\theta_l)\mathbf{b}^H(\theta_l) \otimes \mathbf{I}_NJ=E{jjH}=l=1∑L​σJl​2​b(θl​)bH(θl​)⊗IN​

总的接收数据快照写为：

$$\mathbf{z}=\xi \mathbf{b}(\theta )\otimes \mathbf{a}(r,\theta )+\mathbf{j}+\mathbf{n}$$

其中$\mathbf{n}$是独立噪声，假设为零均值白色圆高斯矢量，协方差为${\mathbf{R}}_n={\sigma }^2{\mathbf{I}}_{MN}$。

4. 无模糊距离角度估计算法

4.1 距离依赖补偿策略

与传统MIMO雷达相比，FDA-MIMO雷达的发射导向矢量同时依赖于距离和角度。定义发射空间频率和接收空间频率为：

$$f_{\text{s-T}}=\frac{d_T}{{\lambda }_0}\sin \theta +\frac{2\Delta f}{c}r=f_{\theta }+f_r$$

$$f_{\text{s-R}}=\frac{d_R}{{\lambda }_0}\sin \theta$$

其中$f_r=\frac{2\Delta f}{c}r$和$f_{\theta }=\frac{d_T}{{\lambda }_0}\sin \theta$分别定义为距离频率和角度频率。

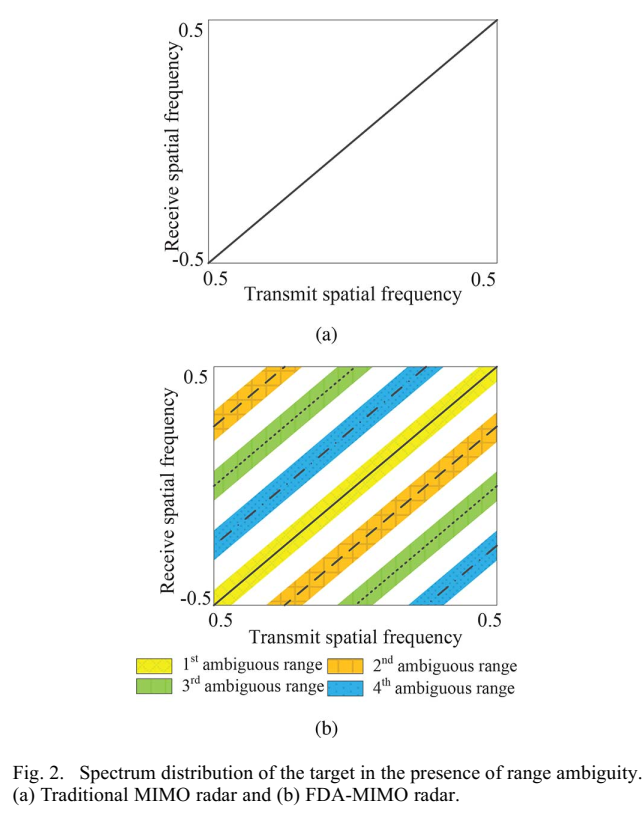
图2描述：图2展示了存在距离模糊时目标在联合发射接收空间频率域的频谱分布。(a)传统MIMO雷达中，目标频谱沿对角线分布，无法区分不同的模糊距离。(b)FDA-MIMO雷达中，经过补偿后，来自不同模糊距离的目标出现在不同的频带中，第一、第三和第四模糊距离的目标清晰可见。

4.2 距离模糊解决方案

在存在距离模糊的情况下，目标的真实距离写为：

$$r=r_b+{\hat{r}}_{\Delta }+(\hat{p}-1)r_u$$

其中$r_b$是目标的主距离，$\hat{p}$是目标的距离模糊指标，p^∈{1,2,…,Na}\hat{p} \in \{1,2,\ldots,N_a\}p^​∈{1,2,…,Na​}，$N_a=\lceil r_{\max }/r_u\rceil$表示模糊距离数，$r_u=c/(2f_{\text{PRF}})$是最大无模糊距离。

定义主距离差为：

$$r_{\Delta }=r-r_b-(\hat{p}-1)r_u$$

这是一个在$[-c/(4B),c/(4B)]$内均匀分布的随机变量，其中$B$是发射信号的带宽。

发射空间频率域的补偿矢量可以表示为：

$${\mathbf{c}}_{\text{comp}}(r_a)=[1,e^{j\frac{4\pi \Delta f}{c}{r}_a},\dots ,e^{j\frac{4\pi \Delta f}{c}(N-1)r_a}{]}^T$$

补偿后的接收数据可以表示为：

$${\mathbf{z}}_{\text{comp}}=\mathbf{z}\odot [1_M\otimes {\mathbf{c}}_{\text{comp}}(r_a)]$$

4.3 联合估计算法

对于测试的距离单元，将补偿后的数据快照重构为$M\times N$数据矩阵：

$${\mathbf{X}}_{\text{comp}}=\text{mat}({\mathbf{z}}_{\text{comp}})$$

目标角度通过最大似然估计（MLE）估计：

$$\hat{\theta }=\arg \underset{\theta }{\max }\left|\sum _{n=1}^N{\mathbf{w}}_R^H(\theta ){\mathbf{X}}_{\text{comp}}(n)\right|$$

其中${\mathbf{w}}_R(\theta )={\mathbf{Q}}_R^{-1}\mathbf{b}(\theta )$是最小方差无失真响应（MVDR）自适应权重。

图3描述：图3展示了关于距离模糊指标的归一化距离频率分布区域。在给定估计角度$\hat{\theta }=4°$和$v=1/4$时，阴影区域表示具有相应距离模糊指标$p$的目标可能的距离频率值。由于$p$是整数，如果相邻模糊距离之间没有重叠，就可以准确确定。

距离模糊指标估计为：

$$\hat{p}=\arg \underset{p=1,2,\dots ,N_a}{\max }|{\mathbf{w}}^H(p,\hat{\theta }){\mathbf{z}}_{\text{comp}}|$$

使用估计的角度和距离模糊指标，主距离差估计为：

$${\hat{r}}_{\Delta }=\arg \underset{r_{\Delta }}{\max }|{\mathbf{w}}^H(p,r_{\Delta },\hat{\theta }){\mathbf{z}}_{\text{comp}}|$$

最终，目标距离估计为：

$$\hat{r}=r_b+{\hat{r}}_{\Delta }+(\hat{p}-1)r_u$$

5. 频率增量的优化选择

5.1 约束条件分析

为了准确确定距离模糊指标，频率增量应满足以下条件。将$\Delta f/f_{\text{PRF}}$的比值分解为：

$$\frac{\Delta f}{f_{\text{PRF}}}=q+v$$

其中$q\in \mathbb{N}$且$v\in [0,1)$。代入补偿后的距离频率表达式：

$${\hat{f}}_{r-\text{comp}}=\frac{2\Delta f}{c}{r}_{\Delta }-(p-1)v$$

注意整数$q$已被丢弃，因为空间频率的周期性。为了确保不同$p$值目标的可区分性，必须满足：

$$v>0$$

$$\max |{\hat{f}}_{r-\text{comp}}|<1$$

$$\max \left|\frac{2\Delta f}{c}{r}_{\Delta }\right|<\frac{v}{2}$$

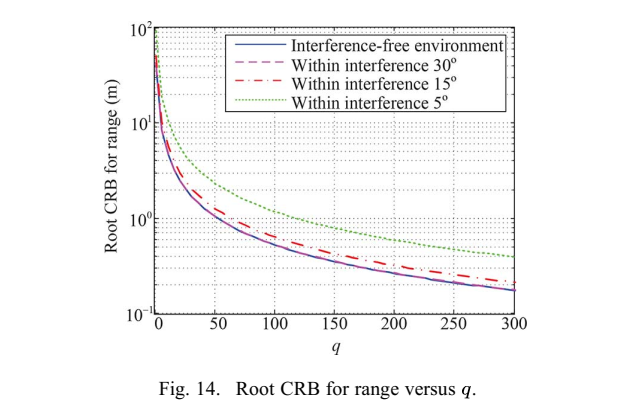
图14描述：图14展示了距离的根CRB与整数$q$的关系。可以观察到，随着频率增量增加，距离估计精度得到改善。然而，为了实现距离模糊解决，频率增量应小于$B/(2N_a)$。因此，当频率增量选择为最大允许值时，可以达到最大改进。

5.2 最优频率增量

基于上述约束，频率增量的最优选择为：

$$\Delta f=\max \{(q+v)f_{\text{PRF}}\},q\in \mathbb{N}$$

满足条件：

$$v=\frac{1}{N_a},\Delta f\le \frac{vB}{2}=\frac{B}{2N_a}$$

根据公式，频率增量可以从一系列离散值中最优选择。如前所述，较大的频率增量可以提高距离估计精度。

6. 性能分析

6.1 克拉美罗界推导

未知参数矢量为$\mathbf{\alpha }=[r,\theta {]}^T$。Fisher信息矩阵（FIM）为：

F=2KEN∣ξ∣2[Re{wrHwr}Re{wrHwθ}Re{wrHwθ}Re{wθHwθ}]\mathbf{F} = \frac{2KE}{N}|\xi|^2 \begin{bmatrix} \text{Re}\{\mathbf{w}_r^H\mathbf{w}_r\} & \text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\} \\ \text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\} & \text{Re}\{\mathbf{w}_\theta^H\mathbf{w}_\theta\} \end{bmatrix}F=N2KE​∣ξ∣2[Re{wrH​wr​}Re{wrH​wθ​}​Re{wrH​wθ​}Re{wθH​wθ​}​]

其中$K$是快照数，辅助向量定义为：

$${\mathbf{w}}_r={\mathbf{Q}}^{-1}{\mathbf{u}}_r,{\mathbf{w}}_{\theta }={\mathbf{Q}}^{-1}{\mathbf{u}}_{\theta }$$

$${\mathbf{u}}_r=\frac{\partial \mathbf{u}(r,\theta )}{\partial r},{\mathbf{u}}_{\theta }=\frac{\partial \mathbf{u}(r,\theta )}{\partial \theta }$$

6.2 无干扰环境下的闭式CRB

在无干扰环境下（$\mathbf{Q}={\sigma }^2{\mathbf{I}}_{MN}$），距离和角度的CRB以及耦合关系为：

$$D_r=\frac{1}{2K\text{SNR}MN}\cdot \frac{1}{(N^2-1){\kappa }_r^2+(M^2-1){\kappa }_R^2{\kappa }_{\theta }^2}$$

$$D_{\theta }=\frac{1}{2K\text{SNR}MN(M^2-1){\kappa }_R^2}$$

$$D_{r\theta }=-\frac{1}{2K\text{SNR}MN(M^2-1){\kappa }_r{\kappa }_R^2}$$

其中$\text{SNR}=(E|\xi {|}^2)/(N{\sigma }^2)$是输入信噪比，${\kappa }_r=4\pi \Delta f/c$，${\kappa }_R=2\pi d_R\cos \theta /{\lambda }_0$，${\kappa }_T=2\pi d_T\cos \theta /{\lambda }_0$。

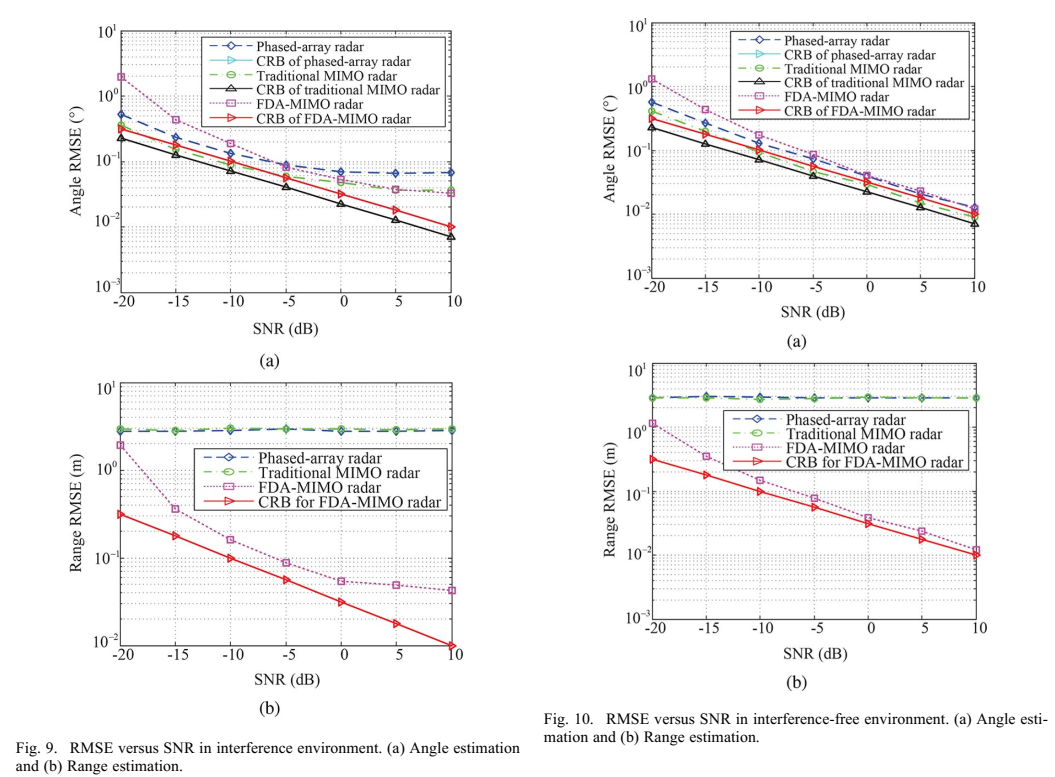
图9和图10描述：图9展示了干扰环境下RMSE随SNR的变化。可以观察到：(a)角度估计在高SNR下存在偏差；(b)FDA-MIMO雷达的距离估计精度随SNR增加显著提高，而传统MIMO雷达的精度无法改善。图10展示了无干扰环境下的结果，FDA-MIMO雷达的RMSE非常接近CRB。

6.3 性能改善分析

考虑同址MIMO雷达具有相同的发射和接收阵列单元，即$d_T=d_R=d$，$M=N$，可以得到：

$$D_r=\frac{1}{6K\text{SNR}{\pi }^2(N^2-1)}{\left(\frac{c}{2N\Delta f}\right)}^2$$

$$D_{\theta }=\frac{1}{2K\text{SNR}{\pi }^2{\cos }^2\theta N^2(N^2-1)d^2}$$

通过增加频率增量，可以实现更准确的距离估计。根据分析，频率增量的上界为$B/(2N_a)$。因此：

$$D_r\ge \frac{1}{2K\text{SNR}{\pi }^2{N}^2(N^2-1)}{\left(\frac{c}{2B}\right)}^2$$

根据此公式，CRB可以降低$24N_a^2/(2K\text{SNR}{\pi }^2{N}^2(N^2-1))$倍，相比传统雷达距离分辨率$c/(2B)$。因此，距离估计的精度可以得到改善。

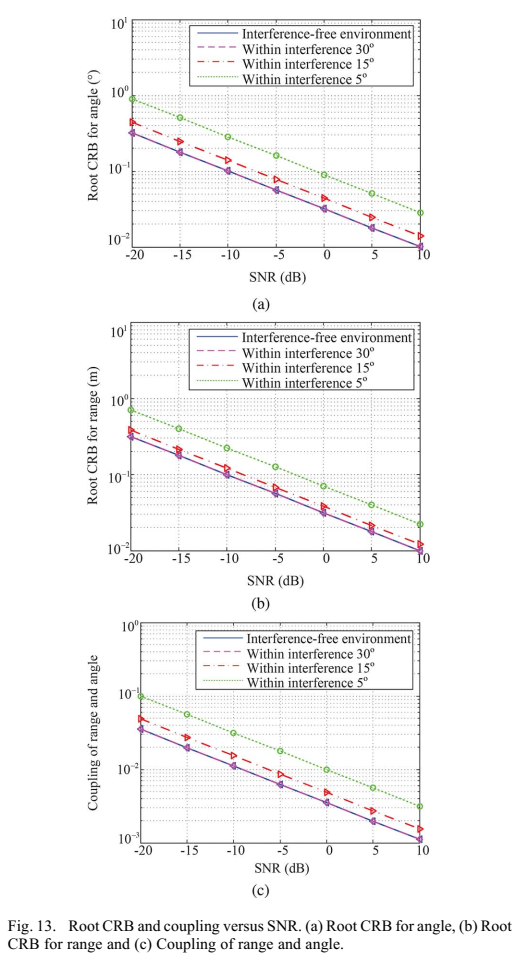
图13描述：图13展示了角度为$0°$的目标的根CRB和耦合关系随SNR的变化。(a)角度的根CRB，(b)距离的根CRB，©距离和角度之间的耦合。可以看到，无干扰环境下的根CRB低于干扰环境。当干扰角度接近目标角度时，根CRB变大。距离的根CRB远小于无干扰环境下的距离分辨率（10米）。

7. 仿真结果与讨论

7.1 仿真参数设置

仿真参数设置如下：参考频率$f_0=10$ GHz，频率增量$\Delta f=30125$ Hz，PRF为5000 Hz，元素数量$N=M=10$，天线间距$d_T=d_R=0.015$ m，脉冲数200，最大无模糊距离30 km，带宽15 MHz，距离分辨率10 m，干扰角度$30°$，INR为30 dB。

7.2 Capon频谱分布

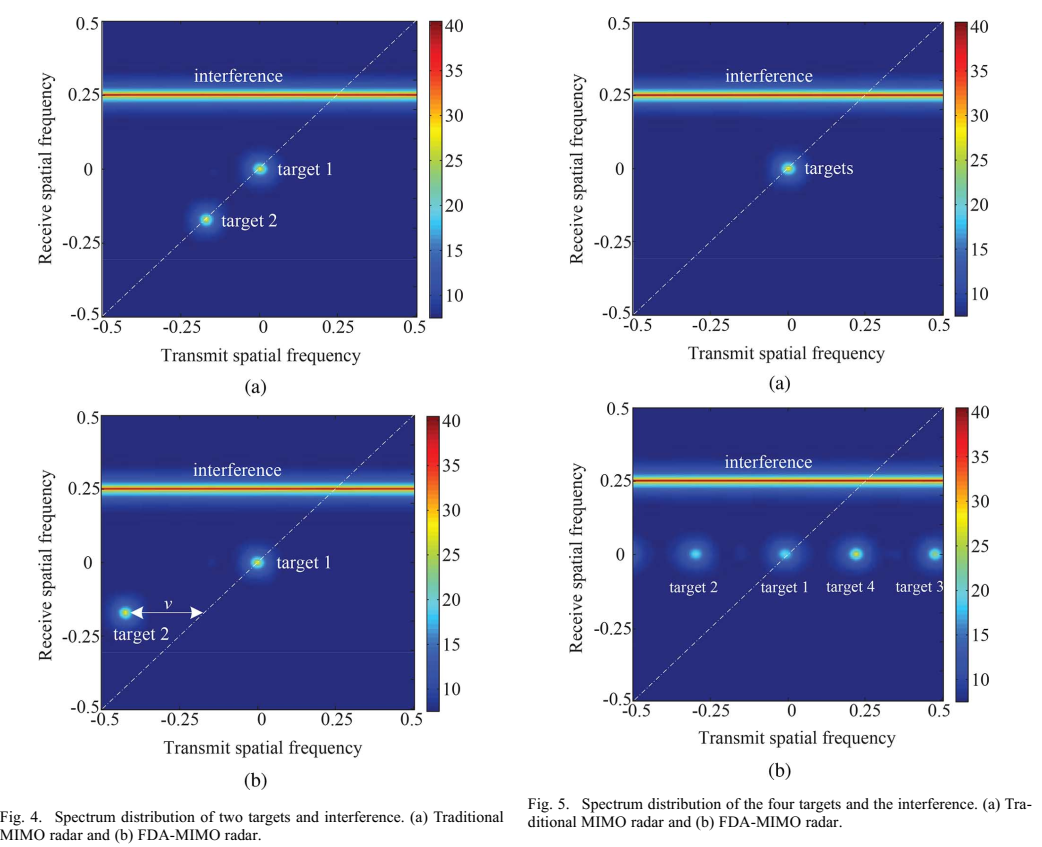
图4和图5详细描述：图4展示了两个目标和干扰在联合发射接收空间频率域的频谱分布。第一个目标在第一模糊距离区域（主距离区域），第二个目标在第二模糊距离区域。在传统MIMO雷达中（图4a），两个目标都呈对角分布。在FDA-MIMO雷达中（图4b），第二个目标在发射空间频率域偏移了$v=0.25$。

图5展示了四个来自相同角度但不同模糊距离区域的目标。在传统MIMO雷达中（图5a），四个目标在联合发射接收维度重叠。在FDA-MIMO雷达中（图5b），四个目标可以明确区分，分别属于对应距离模糊指标的4个频带。

7.3 距离分辨能力

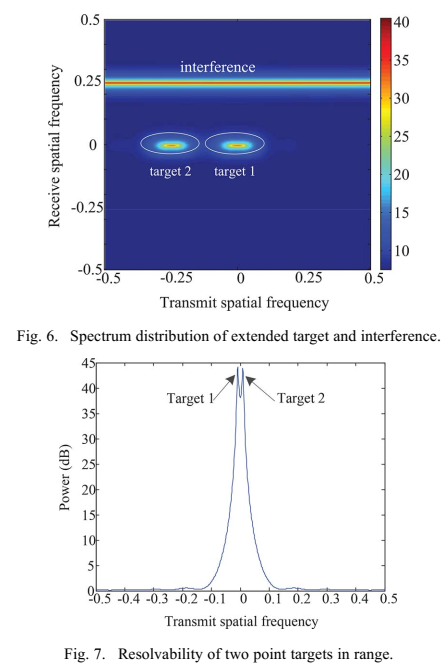
图6和图7描述：图6展示了FDA-MIMO雷达中扩展目标和干扰的频谱分布。目标频谱在发射维度扩展。由于频谱宽度受约束条件限制，这两个目标可以清晰区分。

图7展示了同一距离单元和同一模糊距离区域内两个点目标的频谱。两个目标之间的距离为5米。可以看到，两个目标可以相互区分。因此，距离分辨能力比传统雷达至少高2倍。

7.4 参数估计性能

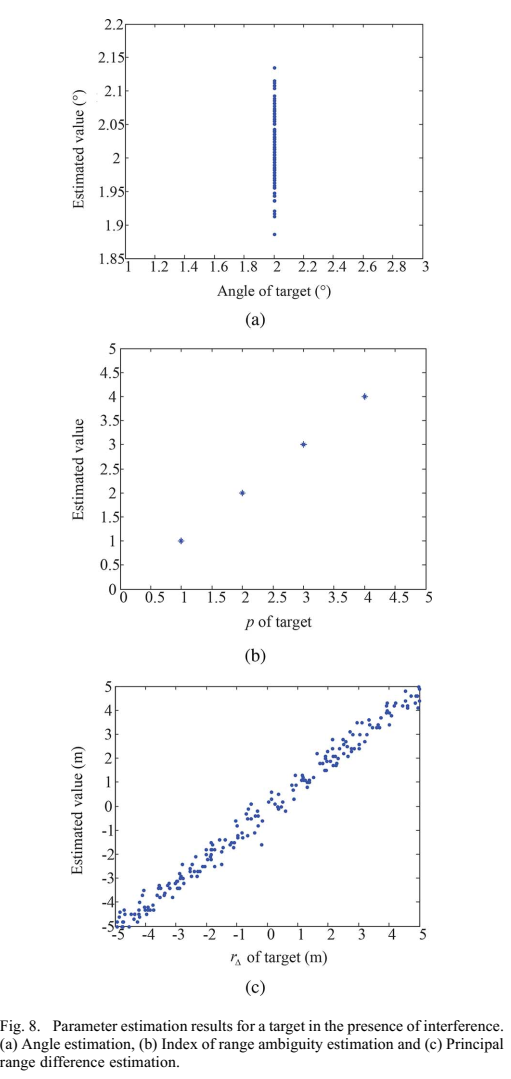
图8描述：图8展示了存在干扰时目标的参数估计结果。(a)角度估计非常接近真实值，(b)距离模糊指标的估计值完全等于真实值，©主距离差的估计值接近真实对应值。因此，使用所提方法，距离模糊得到解决，距离估计精度显著提高。

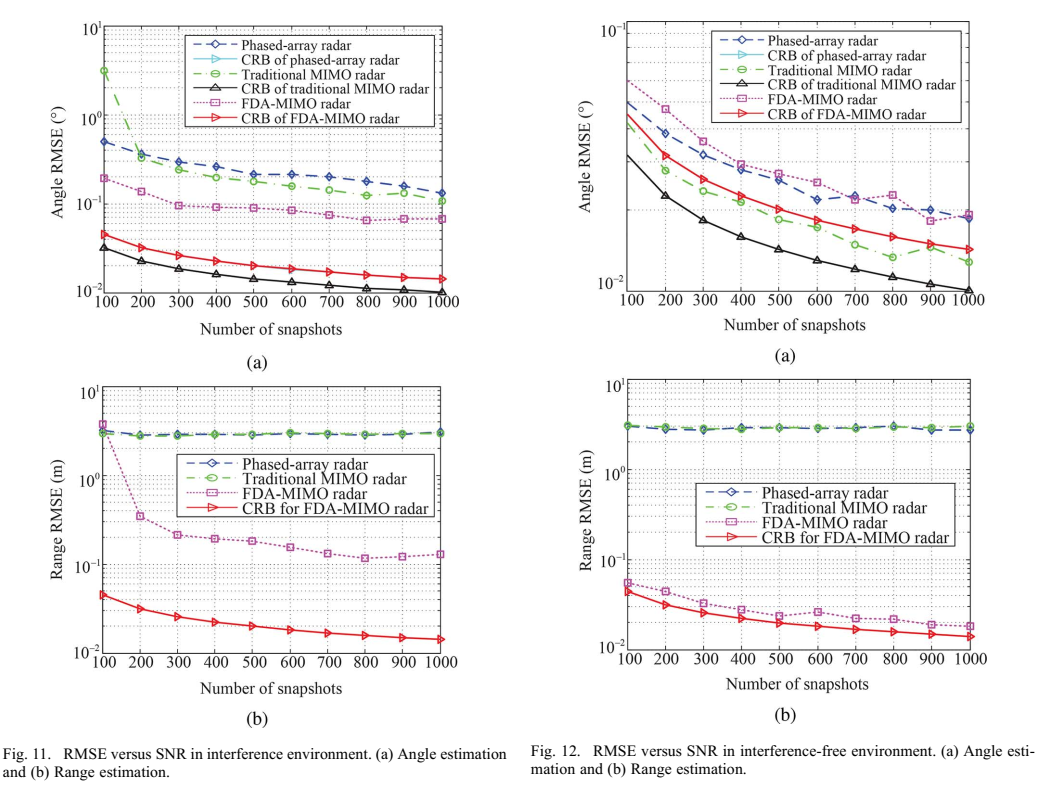
图11和图12描述：图11和图12展示了SNR = 0 dB时RMSE随快照数的变化。图11显示，在干扰环境下，FDA-MIMO雷达的距离和角度估计精度高于相控阵雷达和传统MIMO雷达。图12显示，在无干扰环境下，FDA-MIMO雷达的距离和角度RMSE非常接近CRB。

8. 结论

本文针对高PRF雷达的距离模糊问题，提出了一种基于FDA-MIMO雷达的无模糊距离角度联合估计方法。该方法巧妙利用了FDA-MIMO雷达发射导向矢量的距离角度依赖特性，通过在联合发射接收空间频率域引入可控的自由度，实现了距离模糊的解决和距离估计精度的显著提高。

主要贡献包括：(1)建立了FDA-MIMO雷达的信号模型，揭示了发射导向矢量的距离角度依赖特性；(2)提出了基于距离补偿的联合估计算法，可以同时解决距离模糊并提高估计精度；(3)推导了频率增量的优化选择准则；(4)推导了距离和角度参数的克拉美罗界，分析了参数耦合关系。

---

附录A：已知反射系数时的CRB推导

当反射系数$\xi$已知时，目标参数矢量变为$\mathbf{\alpha }=[r,\theta {]}^T$。距离和角度的CRB可以表示为：

$${\mathbf{D}}_{\mathbf{\alpha }}^{-1}=\mathbf{F}=\frac{2KE}{N}|\xi {|}^2\text{Re}\left\{\left[\begin{array}{c}{\frac{\partial \mathbf{u}(r,\theta )}{\partial r}}^H{\mathbf{Q}}^{-1}\frac{\partial \mathbf{u}(r,\theta )}{\partial r}\end{array}\right]\right\}$$

在这种情况下，FIM可以表示为：

F=2KEN∣ξ∣2[∥wr∥2Re{wrHwθ}Re{wrHwθ}∥wθ∥2]\mathbf{F} = \frac{2KE}{N}|\xi|^2\begin{bmatrix}\|\mathbf{w}_r\|^2 & \text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\} \\ \text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\} & \|\mathbf{w}_\theta\|^2\end{bmatrix}F=N2KE​∣ξ∣2[∥wr​∥2Re{wrH​wθ​}​Re{wrH​wθ​}∥wθ​∥2​]

因此，闭式CRB为：

Dr=N2KE∣ξ∣2∥wθ∥2∥wr∥2∥wθ∥2−(Re{wrHwθ})2D_r = \frac{N}{2KE|\xi|^2}\frac{\|\mathbf{w}_\theta\|^2}{\|\mathbf{w}_r\|^2\|\mathbf{w}_\theta\|^2 - (\text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\})^2}Dr​=2KE∣ξ∣2N​∥wr​∥2∥wθ​∥2−(Re{wrH​wθ​})2∥wθ​∥2​

Dθ=N2KE∣ξ∣2∥wr∥2∥wr∥2∥wθ∥2−(Re{wrHwθ})2D_\theta = \frac{N}{2KE|\xi|^2}\frac{\|\mathbf{w}_r\|^2}{\|\mathbf{w}_r\|^2\|\mathbf{w}_\theta\|^2 - (\text{Re}\{\mathbf{w}_r^H\mathbf{w}_\theta\})^2}Dθ​=2KE∣ξ∣2N​∥wr​∥2∥wθ​∥2−(Re{wrH​wθ​})2∥wr​∥2​

附录B：矩阵$\tilde{\mathbf{G}}$的行列式推导

在无干扰环境下，需要计算矩阵$\tilde{\mathbf{G}}$的行列式。首先，我们有：

G~=∣ξ∣2σ2[∥ur∥2Re{urHuθ}Re{urHuθ}∥uθ∥2]\tilde{\mathbf{G}} = \frac{|\xi|^2}{\sigma^2}\begin{bmatrix}\|\mathbf{u}_r\|^2 & \text{Re}\{\mathbf{u}_r^H\mathbf{u}_\theta\} \\ \text{Re}\{\mathbf{u}_r^H\mathbf{u}_\theta\} & \|\mathbf{u}_\theta\|^2\end{bmatrix}G~=σ2∣ξ∣2​[∥ur​∥2Re{urH​uθ​}​Re{urH​uθ​}∥uθ​∥2​]

其中：

$$\Vert \mathbf{u}{\Vert }^2=MN$$

$$\Vert {\mathbf{u}}_r{\Vert }^2={\kappa }_r^{2}M\sum _{n=1}^N(n-1{)}^2={\kappa }_r^{2}MN(N^2-1)/3$$

$$\Vert {\mathbf{u}}_{\theta }{\Vert }^2={\kappa }_R^{2}N\sum _{m=1}^M(m-1{)}^2+{\kappa }_T^{2}M\sum _{n=1}^N(n-1{)}^2$$

$$={\kappa }_R^{2}N\frac{M(M^2-1)}{3}+{\kappa }_T^{2}M\frac{N(N^2-1)}{3}$$

内积项为：

$${\mathbf{u}}_r^H{\mathbf{u}}_{\theta }=-j{\kappa }_{r}M\sum _{n=1}^N(n-1)=-j{\kappa }_{r}MN(N-1)/2$$

因此，矩阵$\tilde{\mathbf{G}}$的行列式为：

det⁡(G~)=∣ξ∣4σ4[∥ur∥2∥uθ∥2−∣Re{urHuθ}∣2]\det(\tilde{\mathbf{G}}) = \frac{|\xi|^4}{\sigma^4}\left[\|\mathbf{u}_r\|^2\|\mathbf{u}_\theta\|^2 - |\text{Re}\{\mathbf{u}_r^H\mathbf{u}_\theta\}|^2\right]det(G~)=σ4∣ξ∣4​[∥ur​∥2∥uθ​∥2−∣Re{urH​uθ​}∣2]

$$=\frac{|\xi {|}^4}{{\sigma }^4}\left[\frac{G_{11}{G}_{12}}{9}-\frac{G_{21}{G}_{22}}{4}\right]$$

其中：

$$G_{11}={\kappa }_r^{2}MN(N^2-1)$$
$$G_{12}={\kappa }_R^{2}NM(M^2-1)+{\kappa }_T^{2}MN(N^2-1)$$
KaTeX parse error: Can't use function '$' in math mode at position 11: G_{21} = 0$̲（因为实部为零） G_{22} = \kappa_r^2M2N^2(N-1)2$$

最终得到：

$$\det (\tilde{\mathbf{G}})=\frac{|\xi {|}^4}{{\sigma }^4}\cdot \frac{{\kappa }_r^{2}MN(N^2-1)}{9}\cdot [{\kappa }_R^{2}NM(M^2-1)+{\kappa }_T^{2}MN(N^2-1)]$$

这个结果用于计算无干扰环境下的CRB闭式表达式。

附录C：最小均方误差波束形成器推导

在估计了角度、距离模糊指标和主距离差后，最小均方误差（MMSE）波束形成器可以表示为：

$$\hat{\xi }={\mathbf{w}}_{\text{MMSE}}^H{\mathbf{z}}_{\text{comp}}={\mu }_{\text{MMSE}}{\mathbf{u}}^H(\hat{p},{\hat{r}}_{\Delta },\hat{\theta }){\mathbf{Q}}^{-1}{\mathbf{z}}_{\text{comp}}$$

其中自适应权重计算为：

$${\mathbf{w}}_{\text{MMSE}}={\mu }_{\text{MMSE}}{\mathbf{Q}}^{-1}\mathbf{u}(\hat{p},{\hat{r}}_{\Delta },\hat{\theta })$$

标量因子为：

$${\mu }_{\text{MMSE}}=\frac{b_L^2}{1+b_L^2\gamma }$$

或者对于最小最大均方误差波束形成器：

$${\mu }_{\text{MMSE}}=\frac{1}{\gamma }\left(1-\frac{1}{\sqrt{(1+b_L^2\gamma )(1+b_U^2\gamma )}}\right)$$

其中$b_L^2=E|\xi {|}^2/(N{\sigma }^2)$，$b_U^2=E|\xi {|}^2$，$\gamma ={\mathbf{u}}^H(\hat{p},{\hat{r}}_{\Delta },\hat{\theta }){\mathbf{Q}}^{-1}\mathbf{u}(\hat{p},{\hat{r}}_{\Delta },\hat{\theta })$。

这种波束形成器在存在参数估计误差时提供了鲁棒的目标检测性能。