【机器学习07】 激活函数精讲、Softmax多分类与优化器进阶

---

视频链接
吴恩达机器学习p57-69

---

激活函数 (Activation Functions)

激活函数是神经网络的核心组成部分，它为模型引入了非线性表达能力，这是神经网络能够学习复杂模式的基础。

激活函数的作用：需求预测实例

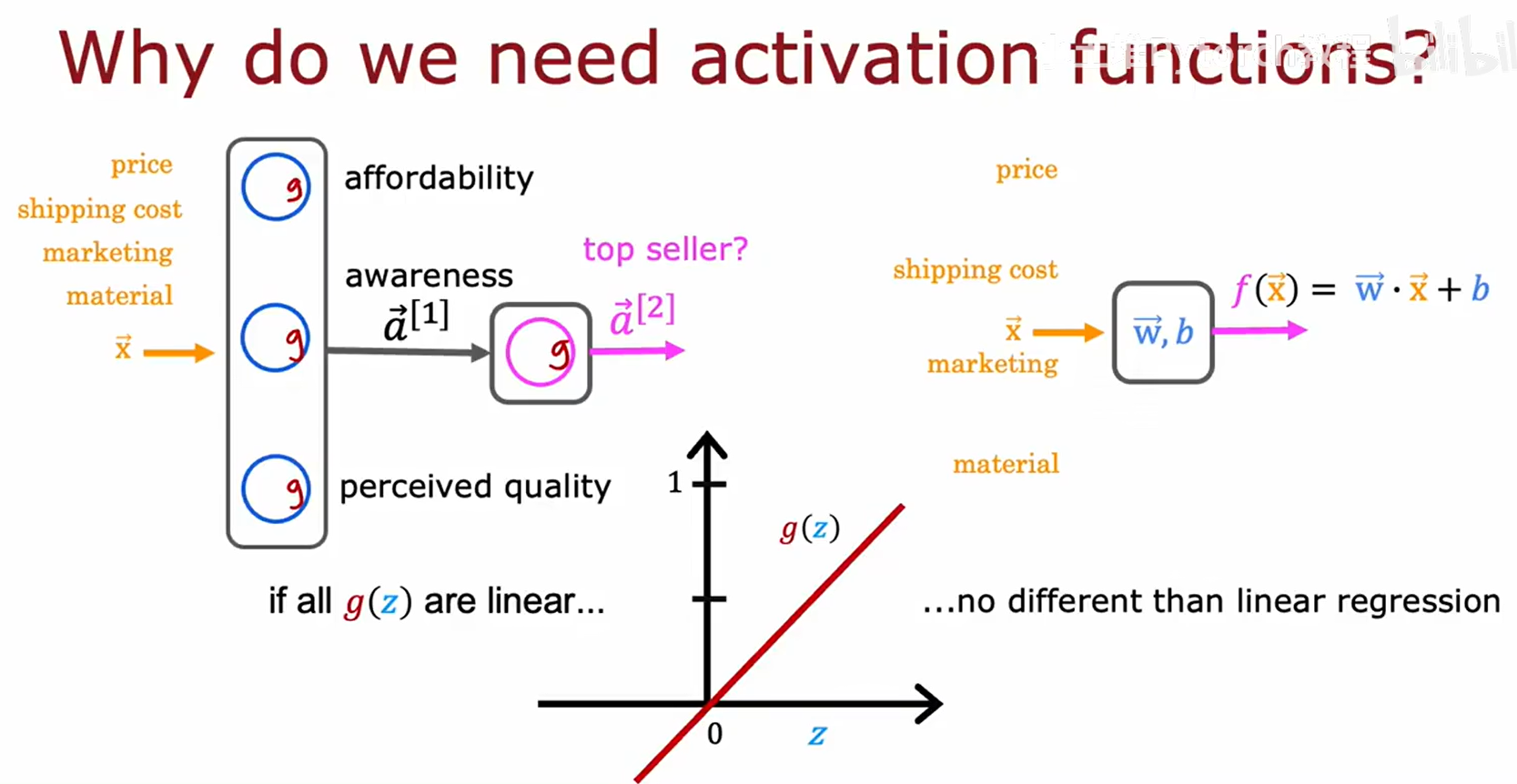
我们通过一个“需求预测”的例子来理解激活函数在神经网络中的具体作用。模型的输入是商品特征，如价格（price）、运费（shipping cost）等。隐藏层的作用是学习更抽象的特征，如“支付能力（affordability）”和“品牌认知度（awareness）”。

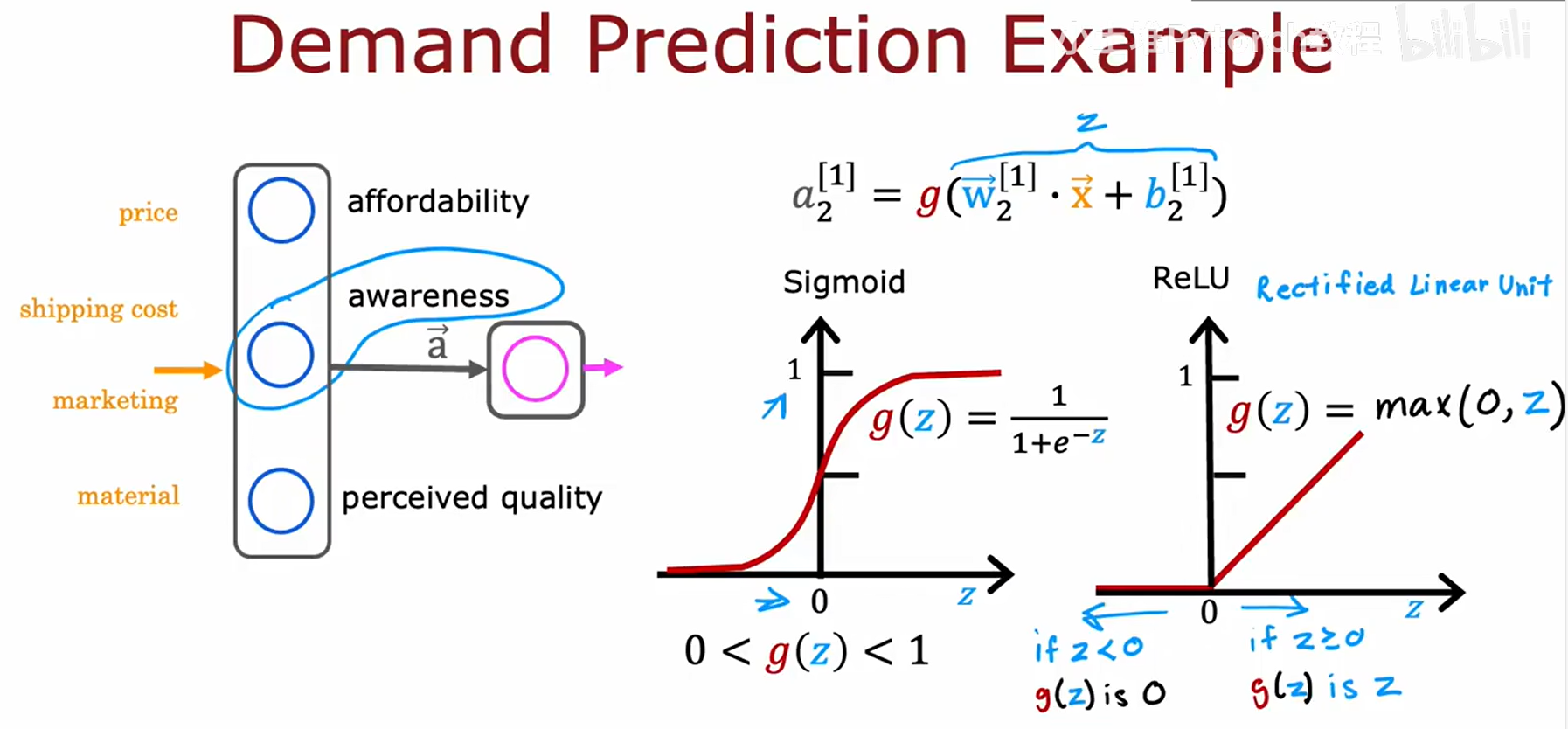
单个神经元的计算过程包含两个步骤：

1. 线性计算：输入与权重进行加权求和，并加上偏置，得到 $z=\vec{w}\cdot \vec{x}+b$。
2. 激活计算：将线性结果 $z$ 输入激活函数 $g$，得到输出 $a=g(z)$。

图右侧展示了两种关键的激活函数：

• Sigmoid 函数：$g(z)=\frac{1}{1+e^{-z}}$，将输出压缩到 (0, 1) 区间，常用于表示概率。
• ReLU (Rectified Linear Unit)：$g(z)=\max (0,z)$，当输入为正时原样输出，为负时输出0，计算效率高。

常见激活函数

除了Sigmoid和ReLU，线性激活函数也是一个基础选项。

上图汇总了三种基本激活函数：

• 线性激活函数 (Linear activation function)：表达式为 $g(z)=z$，即输入等于输出，也被称为“无激活函数”。
• Sigmoid 激活函数：S形曲线，输出范围 (0, 1)。
• ReLU 激活函数：在 $z\ge 0$ 时为线性，在 $z<0$ 时为0。

如何为网络的每一层选择激活函数

这是一个关键的工程决策，不同层有不同的选择标准。

输出层 (Output Layer) 的选择

输出层的激活函数由任务类型和标签 y 的取值范围决定。

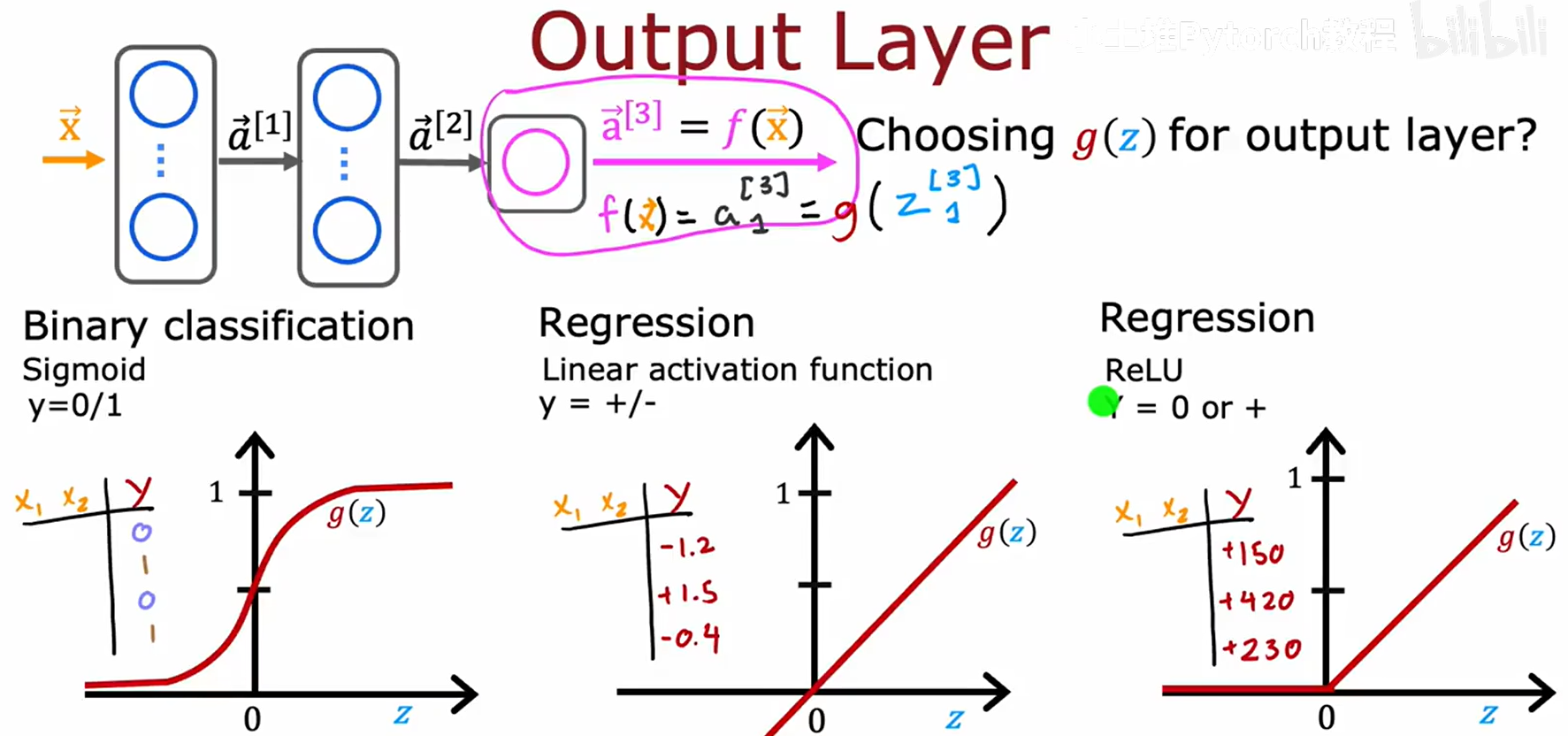
• 二分类问题 (Binary classification)：目标 y 为 0 或 1。需要输出一个概率，应选择 Sigmoid。
• 回归问题 (Regression) 且 y 可为负数：目标 y 是任意实数。不希望限制输出范围，应选择线性激活函数 (Linear activation function)。
• 回归问题 (Regression) 且 y 只能为非负数：目标 y 大于等于0。ReLU 函数可以确保输出非负。

隐藏层 (Hidden Layer) 的选择

对于所有隐藏层，ReLU 是最常用且推荐的选择。

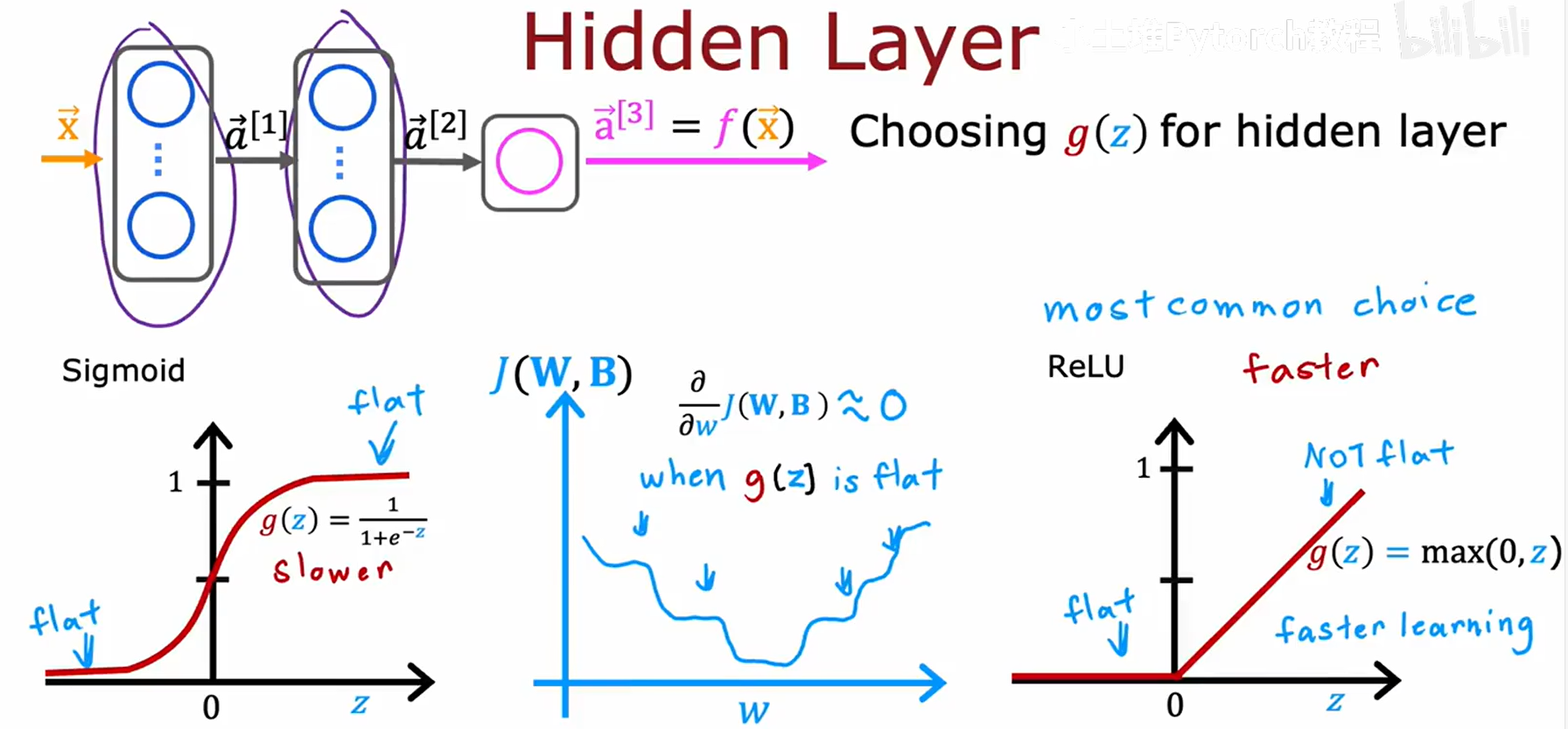
选择ReLU的主要原因是其能有效避免“梯度消失”问题，从而加速训练：

• Sigmoid 的问题：其函数曲线在两端区域非常平坦，导致梯度接近于0，使得参数更新极其缓慢。
• ReLU 的优势：在 $z>0$ 区域，梯度恒为1，保证了梯度的有效传递，使网络学习速度更快。

选择策略总结与 TensorFlow 代码实践

我们将上述选择策略进行总结并展示其代码实现。

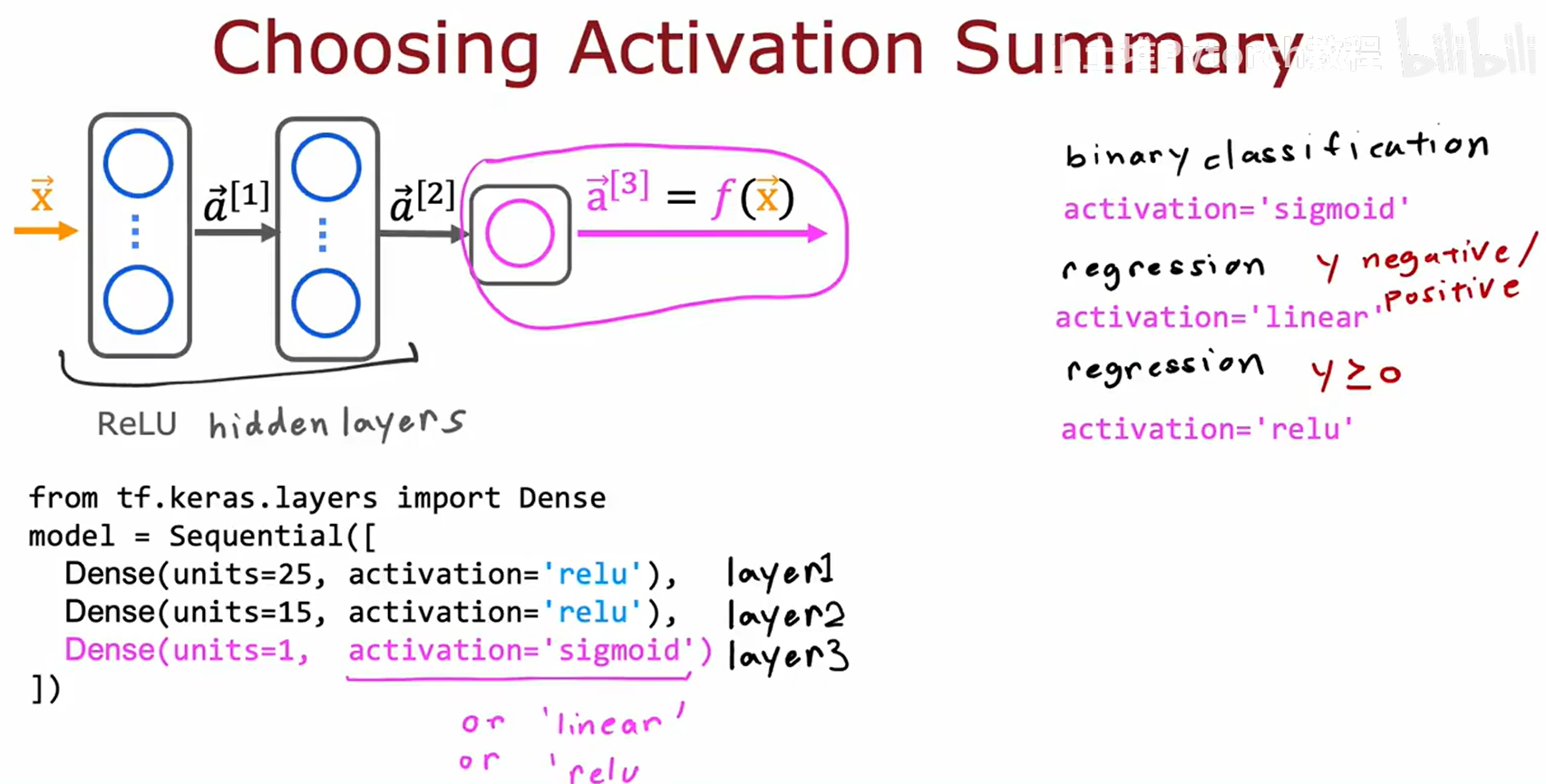
选择策略总结:

• 隐藏层: 使用 ReLU。
• 输出层:
  • 二分类: Sigmoid。
  • 回归 (y可正负): Linear。
  • 回归 (y≥0): ReLU。

TensorFlow/Keras 代码实现:
一个用于二分类任务的三层网络结构示例：

• Layer 1 (隐藏层): 25个单元, relu 激活。
• Layer 2 (隐藏层): 15个单元, relu 激活。
• Layer 3 (输出层): 1个单元, sigmoid 激活。

from tf.keras.layers import Dense
model = Sequential([Dense(units=25, activation='relu'),      # Layer 1Dense(units=15, activation='relu'),      # Layer 2Dense(units=1, activation='sigmoid')     # Layer 3
])

非线性激活函数的必要性

如果所有隐藏层都使用线性激活函数，整个深度网络将退化为一个等效的单层线性模型，失去深度学习的能力。

代数推导证明，一个两层的线性网络 $a^{}=w_1^{}(w_1^{}x+b_1^{})+b_1^{}$ 可以被简化为 $f(x)=wx+b$ 的形式，与单层模型无异。

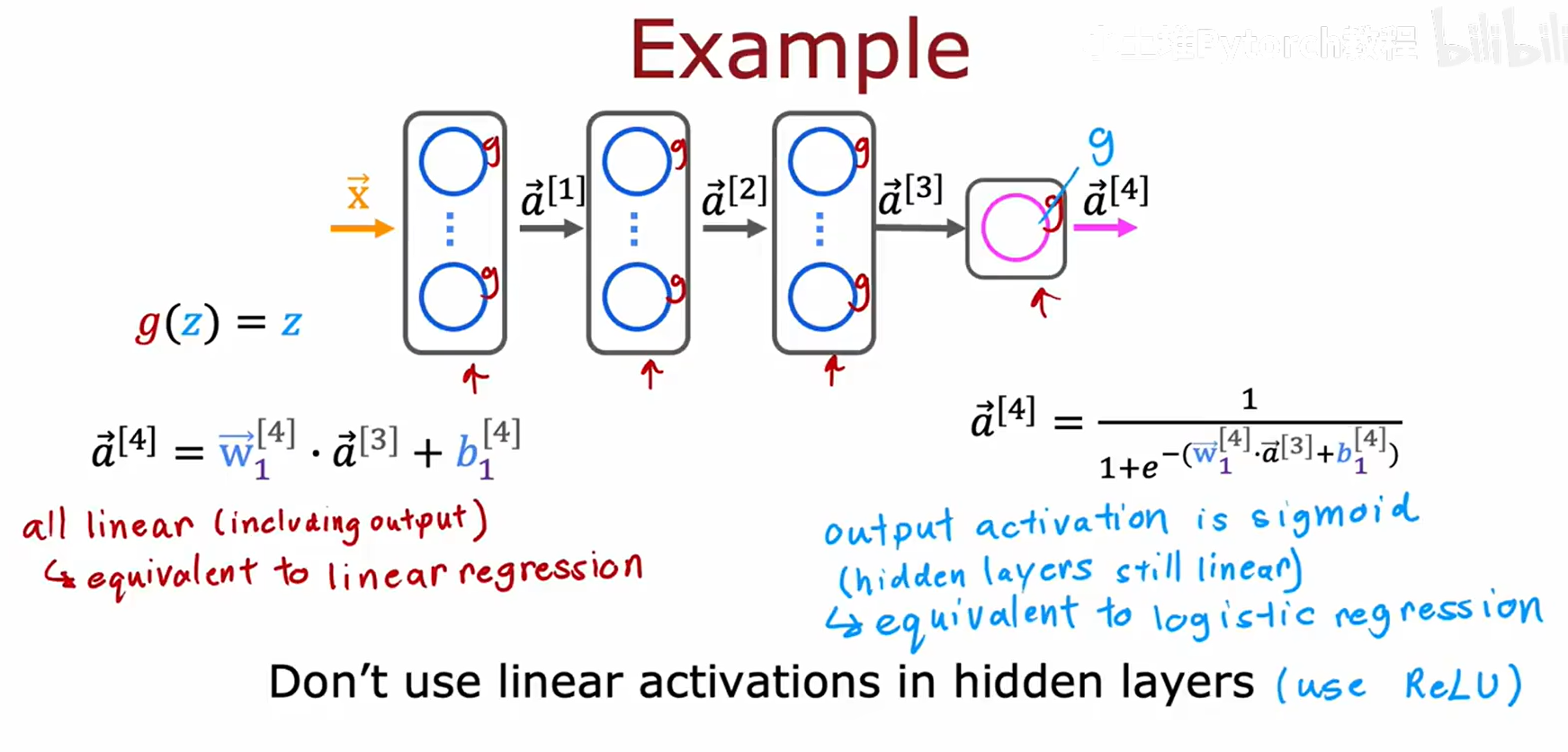
核心结论:

• 如果所有层都是线性的，网络等价于线性回归。
• 如果隐藏层线性、输出层Sigmoid，网络等价于逻辑回归。
• 准则: 禁止在隐藏层中使用线性激活函数，应使用 ReLU。

Softmax回归与多分类

当分类任务的类别超过两个时，需要使用Softmax回归。

多分类问题 (Multiclass Classification)

MNIST手写数字识别是典型的多分类问题，标签 y 可以是 {0, 1, …, 9} 中的一个。

多分类任务需要学习能够分割多个类别的决策边界。

Softmax 回归原理

Softmax是Sigmoid在多分类任务上的推广，用于计算样本属于每个类别的概率。

Softmax 回归计算步骤:

1. 为每个类别 $j$ 计算一个独立的线性得分 $z_j={\vec{w}}_j\cdot \vec{x}+b_j$。
2. 使用Softmax函数将得分转换为概率分布：
   $a_j=P(y=j|\vec{x})=\frac{e^{z_j}}{{\sum }_{k=1}^N{e}^{z_k}}$
   该公式通过归一化，确保所有类别的输出概率之和为1。

Softmax 的损失函数：交叉熵

Softmax回归通常配合交叉熵损失 (Cross-entropy Loss) 使用。

如果一个样本的真实类别是 $j$，其损失仅取决于模型预测为类别 $j$ 的概率 $a_j$：
$loss=-\log a_j$
当预测概率 $a_j$ 趋近1时，损失趋近0；当 $a_j$ 趋近0时，损失趋向无穷大。

将 Softmax 集成到神经网络

一个标准的多分类神经网络结构如下：

• 输入层
• 若干使用 ReLU 的隐藏层
• 一个使用 Softmax 激活的输出层，其神经元数量等于类别总数 $N$。

TensorFlow实现与数值稳定性

在代码实现中，数值稳定性是一个必须考虑的重要问题。

一个有风险的初步实现

一个直接但不被推荐的实现方式如下：

# 不推荐的实现方式
model = Sequential([Dense(units=25, activation='relu'),Dense(units=15, activation='relu'),Dense(units=10, activation='softmax') # 在输出层直接使用 softmax
])
model.compile(loss=SparseCategoricalCrossentropy())

吴恩达老师明确指出不要使用此版本，因为它存在数值稳定性风险。

数值舍入误差 (Numerical Roundoff Errors)

由于计算机浮点数精度有限，数学上等价的计算可能产生不同结果。

如上图Jupyter Notebook所示，两种数学上等价的计算会因舍入误差产生微小差异。在深度学习的迭代计算中，这种误差可能被放大。

使用from_logits=True提升数值稳定性

Softmax和交叉熵涉及的指数和对数运算对精度敏感。将它们分开计算会增加数值不稳定的风险。

推荐的做法是：

1. 让模型的输出层保持线性激活（activation='linear'），直接输出原始的线性得分，这被称为 logits。
2. 将 logits 传递给损失函数，并设置参数 from_logits=True。TensorFlow会使用一个数值上更稳定的内部算法来合并计算Softmax和交叉熵。

最终推荐的代码实现

以下是官方推荐的、更稳健的代码实现模板。

多分类推荐代码:

# 最后一层使用 'linear' 激活
model = Sequential([Dense(units=25, activation='relu'),Dense(units=15, activation='relu'),Dense(units=10, activation='linear') 
])
# 在损失函数中设置 from_logits=True
loss_fn = SparseCategoricalCrossentropy(from_logits=True)
model.compile(..., loss=loss_fn)# 预测时，模型输出的是logits
logits = model(X) 
# 需要概率时，手动调用softmax
f_x = tf.nn.softmax(logits)

二分类推荐代码:

model = Sequential([..., Dense(units=1, activation='linear')])
model.compile(..., loss=BinaryCrossentropy(from_logits=True))
logit = model(X)
f_x = tf.nn.sigmoid(logit) # 手动应用sigmoid

扩展主题

多标签分类 (Multi-label Classification)

多标签分类允许一个样本同时属于多个类别（N选多）。

例如，一张图片可同时被标记为“车”和“行人”。其标签 y 是一个二元向量，如 [1, 0, 1]。

解决方法是构建一个有N个输出单元的网络，并为每个输出单元使用 Sigmoid 激活函数，使其能独立地为每个标签预测一个概率。

Adam 优化算法

梯度下降算法对学习率 $\alpha$ 的选择非常敏感。

Adam (Adaptive Moment Estimation) 算法是一种更高级的优化器，它能为每个参数自适应地调整学习率。

Adam的核心思想是：对梯度持续稳定的参数增大学习率，对梯度来回振荡的参数减小学习率。

在Keras中使用Adam非常简单，它也是目前深度学习任务的首选优化器。

model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-3), loss=...
)

神经网络架构与导数基础

全连接层 vs. 卷积层

我们目前使用的Dense层是全连接层，其每个神经元都与前一层的所有神经元相连。

卷积层 (Convolutional Layer) 的神经元只连接到前一层的一个局部区域。

这使得卷积层在处理图像等结构化数据时，参数更少、计算更快、更不易过拟合。

导数的直观定义

导数是神经网络进行参数更新的依据，其直观意义是“变化放大系数”。

如果导数为 $k$，则输入 $w$ 的微小变化 $ϵ$ 会引起输出 $J(w)$ 产生约 $k\times ϵ$ 的变化。

我们可以使用sympy等符号计算库来求导。

反向传播 (Backpropagation) 简介

反向传播是高效计算神经网络中所有参数梯度的核心算法，它基于微积分的链式法则。

它通过一个计算图，首先进行前向传播计算出最终损失。

然后，从最终损失开始，反向传播梯度，利用链式法则逐层计算出损失对每个参数的导数。

反向传播通过复用中间计算结果，极大地提升了梯度计算的效率。

总结

本文详细探讨了神经网络的几个关键高级主题：

• 激活函数选择：隐藏层用ReLU，输出层根据任务选择。
• Softmax回归：处理多分类问题的理论与实践。
• 编码最佳实践：使用 from_logits=True 提升数值稳定性。
• Adam优化器：使用自适应学习率算法加速并稳定训练。
• 反向传播原理：理解神经网络高效学习的内部机制。