【研究生随笔】Pytorch中的线性回归

线性回归基于⼏个简单的假设：⾸先，假设⾃变量 x 和因变量 y 之间的关系是线性的，即y可以表⽰为 x 中元素的加权和，这⾥通常允许包含观测值的⼀些噪声；其次，我们假设任何噪声都⽐较正常，如噪声遵循正态分布。
举个例子，更好理解：
我们希望根据房屋的⾯积（平⽅英尺）和房龄（年）来估算房屋价格（美元）。为了开发⼀个能预测房价的模型，我们需要收集⼀个真实的数据集。这个数据集包括了房屋的销售价格、⾯积和房龄。在机器学习的术语中，该数据集称为训练数据集（training data set）或训练集（training set），每⾏数据（在这个例⼦中是与⼀次房屋交易相对应的数据）称为样本（sample），也可以称为数据点（data point）或数据样本（data instance）。我们要试图预测的⽬标（在这个例⼦中是房屋价格）称为标签（label）或⽬标（target）。预测所依据的⾃变量（⾯积和房龄）称为 特征（features）或 协变量（covariates）。
通常，我们使⽤ n 来表⽰数据集中的样本数。对索引为 i 的样本，其输⼊表⽰为 x(i) = [x( 1i); x( 2i)]⊤，其对应的标签是 y(i)。
上面的例子的模型可用如下公式进行类比：

其中，ω_area 和 ω_age 称为 权重（weight）， b 称为 偏置（bias），或称为偏移量（offset）、截距（intercept）。权重决定了每个特征对我们预测值的影响。偏置是指当所有特征都取值为0时，预测值应该为多少。即使现实中不会有任何房⼦的⾯积是0或房龄正好是0年，仍然需要偏置项。如果没有偏置项，模型的表达能⼒将受到限制。
将预测结果表示为如下公式：
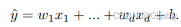如果将权重放到一个向量中来保存或者描述的话，就要可以将过程与之前学的线性代数相关的操作来进行计算了（预测结果即转换为点积的形式来表达）：

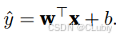
那如果再将特征值换成集合的形式来表达的话，有进一步转换为矩阵和向量的乘法：

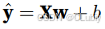
损失函数：

用于确定模型所输出的结果的拟合程度的度量，可以量化实际值和预测值之间的差距，一般是非负数且越小越好。回归问题最常用的是平方误差函数：

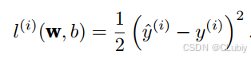
其中，y帽i为样本id预测值，yi为真实值（偷懒下的描述）。

解析解：

线性回归是一个简单的优化问题，他的解可以用一个公式表达出来，这类解就叫解析解（analytical solution），将偏置 b 合并到参数 w中。合并⽅法是在包含所有参数的矩阵中附加⼀列。我们的预测问题是最小化 ∥y − Xw∥^2(范数)。这在损失平⾯上只有⼀个临界点，这个临界点对应于整个区域的损失最小值。将损失关于w的导数设为0，得到解析解：

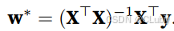
梯度下降：

几乎可以优化所有深度学习的模型，通过不断在损失函数递减的方向上更新参数来降低误差（计算损失函数关于模型参数的导数）。但是如果每一次计算都要对所有的参数进行一次求导的话，那速度会太慢（有大部分的参数是无辜的），所以就会涉及到随机抽取一小批样本来进行计算，这叫做小批量随机梯度下降（minibatchstochastic gradient descent）。
⾸先随机抽样⼀个小批量B，它是由固定数量的训练样本组成的。然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。最后，我们将梯度乘以⼀个预先确定的正数η，并从当前参数的值中减掉。

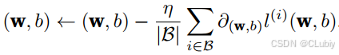
矢量化加速：

在训练模型时，经常需要同时处理一整个小批量的样本，就需要对计算进行矢量化处理，从而利用线性代数库。

正态分布与平方损失：

正太分布（normal distribution）也是高斯分布：若随机变量x具有均值μ和方差σ^2，则其正态分布概率密度函数为：

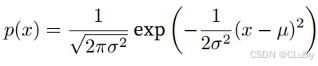
用代码表示如下：

import math
import numpy as np
def normal(x, mu, sigma):p = 1 / math.sqrt(2 * math.pi sigma**2)return p * np.exp(-0.5 / sigma**2 * (x - mu)**2