当前位置：首页 > news >正文

构建AI智能体：七十一、模型评估指南：准确率、精确率、F1分数与ROC/AUC的深度解析

news 2025/10/23 7:43:28

一. 前言

在我们面对项目需求时，构建模型只是第一步，评估其性能并判断它是否真正解决了问题，才是决定项目成败的关键。一个在训练集上表现完美的模型，可能在现实数据面前一败涂地。因此，掌握一套科学的模型评估工具箱至关重要。今天我们将深入剖析准确率、精确率、召回率、F1分数、ROC曲线和AUC等核心指标，并结合实际分类场景拆解它们的适用逻辑与计算本质，让每个指标的价值边界更清晰。

当我们听说一个AI模型有99%的准确率时，我们的第一反应可能是太厉害了！但事实上，这很可能是一个陷阱。我们要厘清事实本质，窥一斑而知全豹，处一隅而观全局，下面我们就拨开迷雾，看懂模型评估的真实面貌。

二、基础指标

1. 混淆矩阵

混淆矩阵是机器学习中用于评估分类模型性能的重要工具。它通过表格形式直观展示模型的预测结果与真实标签的对比情况，让我们能够清楚看到模型在哪些地方做对了，在哪些地方做错了。

核心概念：

对于一个二分类问题，混淆矩阵包含四个关键指标：

TP：真正例 - 模型正确预测为正例
FP：假正例 - 模型错误预测为正例（误报）
FN：假负例 - 模型错误预测为负例（漏报）
TN：真负例 - 模型正确预测为负例

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.metrics import confusion_matrix
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'Segoe UI Symbol', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
# 数据
y_true = [0, 0, 1, 1, 0, 1, 0, 1, 1, 0]
y_pred = [0, 1, 1, 0, 0, 1, 0, 1, 0, 0]# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)# 简单绘图
fig, ax = plt.subplots(figsize=(6, 5))# 为每个格子自定义颜色（示例：二分类的TN/FP/FN/TP）
cell_colors = {(0, 0): 'lightblue',   # TN(0, 1): 'lightcoral',  # FP(1, 0): 'gold',        # FN(1, 1): 'lightgreen'   # TP
}# 构建颜色索引矩阵
unique_colors = list(dict.fromkeys(cell_colors.values()))
color_to_idx = {c: i for i, c in enumerate(unique_colors)}
color_idx = np.zeros_like(cm, dtype=int)
for (r, c), col in cell_colors.items():color_idx[r, c] = color_to_idx[col]from matplotlib.colors import ListedColormap
cmap = ListedColormap(unique_colors)# 使用颜色矩阵绘制背景，并在其上叠加真实的混淆矩阵数值
im = ax.imshow(color_idx, cmap=cmap, vmin=0, vmax=max(color_to_idx.values()))# 在每个格子写入数值
for i in range(cm.shape[0]):for j in range(cm.shape[1]):ax.text(j, i, f"{cm[i, j]}", ha='center', va='center', color='black', fontsize=12)ax.set_title('混淆矩阵')
ax.set_xlabel('预测值')
ax.set_ylabel('真实值')
ax.set_xticks(np.arange(cm.shape[1]))
ax.set_yticks(np.arange(cm.shape[0]))
plt.show()# 打印结果
print("真实值:", y_true)
print("预测值:", y_pred)
print("混淆矩阵:")
print(cm)# 手动计算过程
tp = 0  # 真正例
fp = 0  # 假正例  
fn = 0  # 假负例
tn = 0  # 真负例print("样本逐个分析:")
for i, (true, pred) in enumerate(zip(y_true, y_pred)):if true == 1 and pred == 1:tp += 1result = "TP (真正例)"elif true == 0 and pred == 1:fp += 1result = "FP (假正例)"elif true == 1 and pred == 0:fn += 1result = "FN (假负例)"else:  # true == 0 and pred == 0tn += 1result = "TN (真负例)"print(f"样本{i+1}: {true} -> {pred} | {result}")print(f"\n📊 最终统计:")
print(f"TP (真正例): {tp}")
print(f"FP (假正例): {fp}") 
print(f"FN (假负例): {fn}")
print(f"TN (真负例): {tn}")# 创建对比表格
fig, ax = plt.subplots(figsize=(12, 4))
ax.axis('tight')
ax.axis('off')# 表格数据
table_data = []
headers = ['样本', '真实值', '预测值', '比较结果', '类别']
table_data.append(headers)for i, (true, pred) in enumerate(zip(y_true, y_pred)):if true == pred:if true == 1:category = "TP (真正例)"color = "green"else:category = "TN (真负例)" color = "blue"else:if pred == 1:category = "FP (假正例)"color = "orange"else:category = "FN (假负例)"color = "red"comparison = "正确" if true == pred else "错误"table_data.append([f"样本{i+1}", true, pred, comparison, category])# 创建表格
table = ax.table(cellText=table_data, cellLoc='center', loc='center',colWidths=[0.15, 0.15, 0.15, 0.2, 0.35])# 设置表格样式
table.auto_set_font_size(False)
table.set_fontsize(11)
table.scale(1, 1.6)# 为不同类别设置颜色
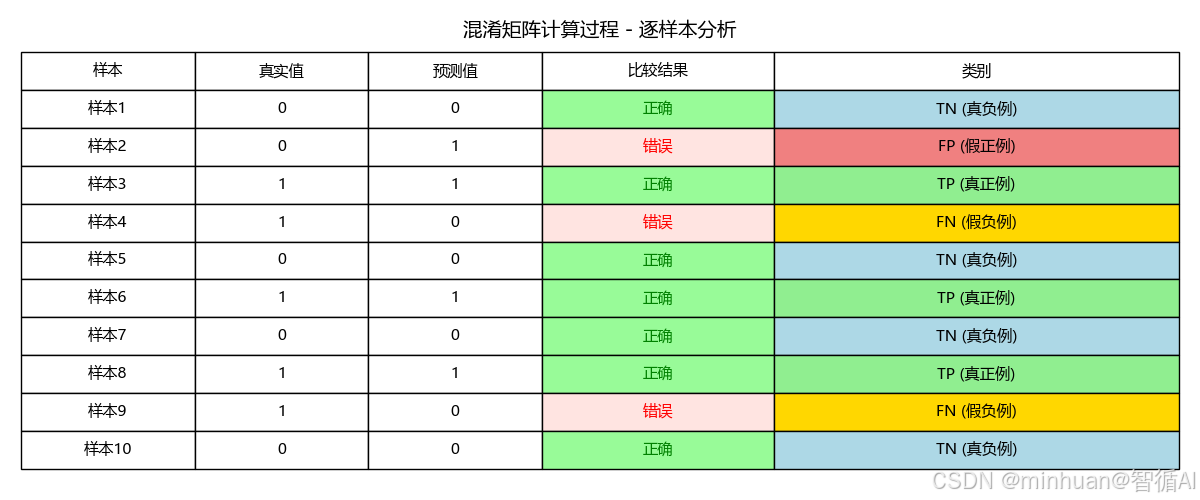
for i in range(1, len(table_data)):# 类别列着色cell = table[i, 4]  # 类别列if "TP" in table_data[i][4]:cell.set_facecolor('lightgreen')elif "TN" in table_data[i][4]:cell.set_facecolor('lightblue') elif "FP" in table_data[i][4]:cell.set_facecolor('lightcoral')elif "FN" in table_data[i][4]:cell.set_facecolor('gold')# 比较结果列着色（正确为绿色，错误为红色）comp_cell = table[i, 3]  # 比较结果列if table_data[i][3] == "正确":comp_cell.set_facecolor('palegreen')comp_cell.get_text().set_color('green')else:  # 错误comp_cell.set_facecolor('mistyrose')comp_cell.get_text().set_color('red')plt.title('混淆矩阵计算过程 - 逐样本分析', fontsize=14, pad=2)
plt.tight_layout(pad=1.5)
plt.show()

输出显示：

真实值: [0, 0, 1, 1, 0, 1, 0, 1, 1, 0]
预测值: [0, 1, 1, 0, 0, 1, 0, 1, 0, 0]
混淆矩阵:
[[4 1]
[2 3]]
样本逐个分析:

样本1: 0 -> 0 | TN (真负例)
样本2: 0 -> 1 | FP (假正例)
样本3: 1 -> 1 | TP (真正例)
样本4: 1 -> 0 | FN (假负例)
样本5: 0 -> 0 | TN (真负例)
样本6: 1 -> 1 | TP (真正例)
样本7: 0 -> 0 | TN (真负例)
样本8: 1 -> 1 | TP (真正例)
样本9: 1 -> 0 | FN (假负例)
样本10: 0 -> 0 | TN (真负例)

📊 最终统计:
TP (真正例): 3
FP (假正例): 1
FN (假负例): 2
TN (真负例): 4

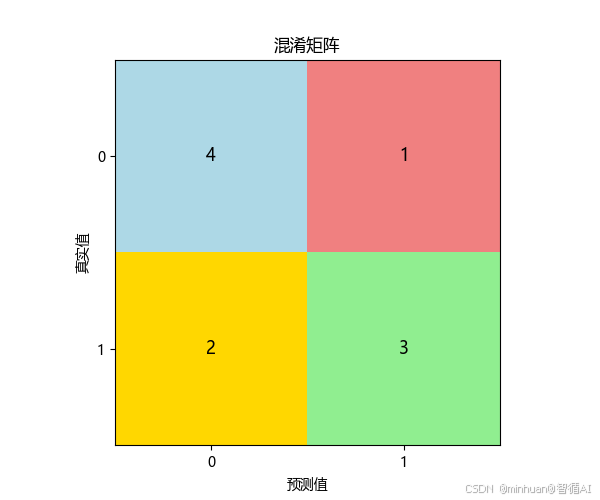
结果说明：

一个标准的混淆矩阵图：

4个格子分别显示 TP, FP, FN, TN
和计算过程统一的颜色区分显示
清晰的坐标轴标签

数字解释：

左上角(TN)：预测正确为负例的数量，正确排除
右上角(FP)：预测错误为正例的数量，误报（假警报）
左下角(FN)：预测错误为负例的数量，漏报（漏掉的真实情况）
右下角(TP)：预测正确为正例的数量，正确识别

2. 准确率

定义：所有预测正确的样本占总样本的比例。
公式：Accuracy = (TP + TN) / (TP + TN + FP + FN)
解读：它给出了一个最直观的整体性能概览。在上例中，准确率 = (5+3)/10 = 80%。
局限性：当数据分布极度不平衡时，准确率会严重失真。例如，在99%是负例的欺诈检测数据中，一个永远预测“非欺诈”的模型，其准确率也能高达99%，但这个模型毫无用处。

accuracy_manual = (tp + tn) / (tp + tn + fp + fn)
print(f"\n1. 准确率 (Accuracy):")
print(f"   公式: (TP + TN) / (TP + TN + FP + FN)")
print(f"   计算: ({tp} + {tn}) / {len(y_true)} = {accuracy_manual:.3f}")
print(f"   含义: 模型整体预测正确率")

准确率 (Accuracy):
公式: (TP + TN) / (TP + TN + FP + FN)
计算: (3 + 4) / 10 = 0.700
含义: 模型整体预测正确率

3. 精确率

定义：在所有被预测为正例的样本中，实际是正例的比例。
公式：Precision = TP / (TP + FP)
解读：它衡量的是模型“不冤枉好人”的能力。高精确率意味着，每当模型发出一个正例信号，这个信号很可能是可靠的。
应用场景：垃圾邮件检测。我们希望被标记为“垃圾”的邮件，尽可能都是真正的垃圾邮件（减少FP），以免误删重要邮件。

precision_manual = tp / (tp + fp) if (tp + fp) > 0 else 0
print(f"\n精确率 (Precision):")
print(f"  公式: TP / (TP + FP)")
print(f"  计算: {tp} / ({tp} + {fp}) = {precision_manual:.4f}")

精确率 (Precision):
公式: TP / (TP + FP)
计算: 3 / (3 + 1) = 0.7500

4. 召回率

定义：在所有实际为正例的样本中，被正确预测为正例的比例。
公式：Recall = TP / (TP + FN)
解读：它衡量的是模型“不放过坏人”的能力。高召回率意味着，模型能够找出绝大部分真正的正例。
应用场景：疾病诊断，我们希望尽可能找出所有真正的患者（减少FN），即使这意味着会让一些健康的人进行二次检查。

recall_manual = tp / (tp + fn) if (tp + fn) > 0 else 0
print(f"\n召回率 (Recall):")
print(f"  公式: TP / (TP + FN)")
print(f"  计算: {tp} / ({tp} + {fn}) = {recall_manual:.4f}")

召回率 (Recall):
公式: TP / (TP + FN)
计算: 3 / (3 + 2) = 0.6000

5. F1分数

定义：精确率和召回率的调和平均数。
公式：F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
解读：精确率和召回率通常相互矛盾，提高一个往往会降低另一个。F1分数提供了一个单一指标来平衡这两者。当需要同时兼顾精确率和召回率，且正负样本分布不平衡时，F1是比准确率更好的指标。

f1_manual = 2 * (precision_manual * recall_manual) / (precision_manual + recall_manual) if (precision_manual + recall_manual) > 0 else 0
print(f"\nF1分数 (F1-Score):")
print(f"  公式: 2 * (Precision * Recall) / (Precision + Recall)")
print(f"  计算: 2 * ({precision_manual:.4f} * {recall_manual:.4f}) / ({precision_manual:.4f} + {recall_manual:.4f}) = {f1_manual:.4f}")

F1分数 (F1-Score):
公式: 2 * (Precision * Recall) / (Precision + Recall)
计算: 2 * (0.7500 * 0.6000) / (0.7500 + 0.6000) = 0.6667

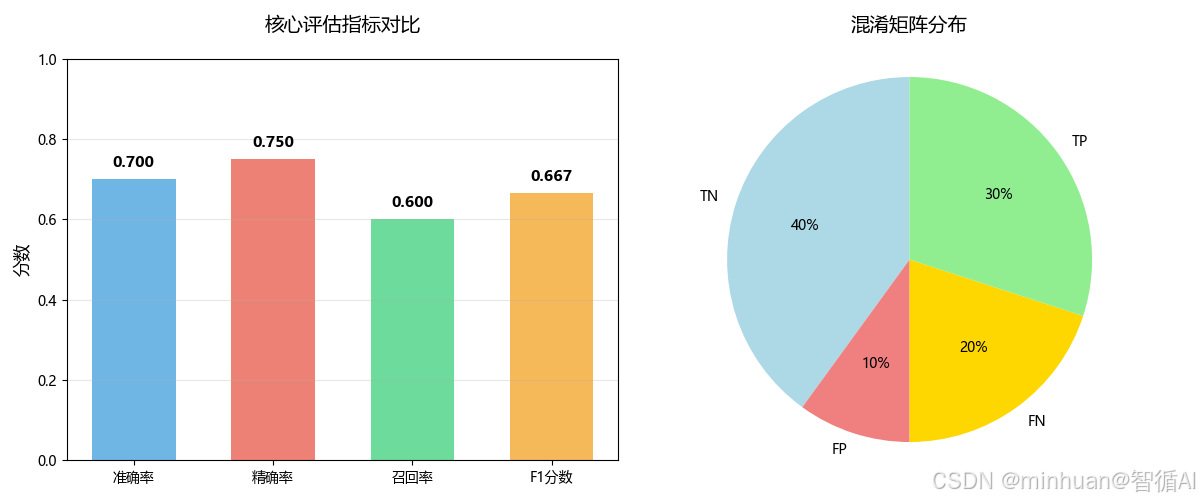
6. 指标图

指标对比条形图与指标关系图

# 2. 指标对比条形图与指标关系图
fig_metrics, axes_metrics = plt.subplots(1, 2, figsize=(12, 5))# 指标对比条形图
ax_bar = axes_metrics[0]
metrics = ['准确率', '精确率', '召回率', 'F1分数']
values = [accuracy_manual, precision_manual, recall_manual, f1_manual]
colors = ['#3498db', '#e74c3c', '#2ecc71', '#f39c12']bars = ax_bar.bar(metrics, values, color=colors, alpha=0.7, width=0.6)
ax_bar.set_ylim(0, 1)
ax_bar.set_title('核心评估指标对比', fontsize=14, pad=20)
ax_bar.set_ylabel('分数', fontsize=12)
ax_bar.grid(True, alpha=0.3, axis='y')# 在条形上添加数值
for bar, value in zip(bars, values):height = bar.get_height()ax_bar.text(bar.get_x() + bar.get_width()/2., height + 0.02,f'{value:.3f}', ha='center', va='bottom', fontsize=11, fontweight='bold')# 指标关系图（混淆矩阵分布）
ax_pie = axes_metrics[1]
categories = ['TN', 'FP', 'FN', 'TP']
counts = [tn, fp, fn, tp]
colors_detail = ['lightblue', 'lightcoral', 'gold', 'lightgreen']
wedges, texts, autotexts = ax_pie.pie(counts, labels=categories, colors=colors_detail,autopct='%1.0f%%', startangle=90)
ax_pie.axis('equal')
ax_pie.set_title('混淆矩阵分布', fontsize=14, pad=20)
plt.tight_layout()
plt.show()

三、综合评估：ROC曲线与AUC

上述指标通常依赖于一个固定的分类阈值（例如，模型输出概率>0.5则判为正例）。但阈值是可以调整的，ROC曲线则通过动态调整阈值，为我们提供了更全面的视角。

1. ROC曲线

定义：以假正率（FPR）为横轴，真正率（TPR，即召回率）为纵轴绘制的曲线。
- FPR = FP / (FP + TN)：所有负例中被误判为正例的比例。我们希望它越低越好。
- TPR = Recall = TP / (TP + FN)
如何绘制：通过不断调整分类阈值，计算出每一组(FPR, TPR)坐标，并将其连接成线。
解读：
- 理想点：左上角(0,1)，即FPR=0（没有误报），TPR=1（全部捕捉）。
- 对角线：从(0,0)到(1,1)，代表一个“随机猜测”模型的性能。任何有意义的模型的ROC曲线都应高于这条线。
- 曲线含义：曲线越靠近左上方，模型的整体性能越好。

2. AUC

定义：ROC曲线下的面积。
取值范围：[0, 1]。
解读：
- AUC = 1.0：完美模型。
- AUC = 0.5：随机模型，无预测能力。
- AUC < 0.5：比随机还差，可能数据或模型有严重问题。
优点：
- 尺度不变：它衡量的是模型排序质量的概率，不受具体分类阈值影响。
- 分类能力稳定：对样本类别分布不敏感，非常适合处理不平衡数据集。

from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score, roc_curve, auc
# 计算ROC曲线和AUC
# 模拟预测概率（用于ROC曲线）
y_pred_proba = [0.1, 0.7, 0.8, 0.4, 0.2, 0.9, 0.3, 0.85, 0.6, 0.25]
fpr, tpr, thresholds = roc_curve(y_true, y_pred_proba)
roc_auc = auc(fpr, tpr)print("\n" + "="*50)
print(" ROC曲线与AUC计算:")
print("="*50)print(f"\nROC曲线坐标点 (FPR, TPR):")
for i, (f, t, thresh) in enumerate(zip(fpr, tpr, thresholds)):print(f"  阈值={thresh:.2f}: FPR={f:.2f}, TPR={t:.2f}")print(f"\nAUC (曲线下面积) = {roc_auc:.3f}")
print("AUC含义:")
print("  • 0.9-1.0: 极好的分类能力")
print("  • 0.8-0.9: 良好的分类能力") 
print("  • 0.7-0.8: 一般的分类能力")
print("  • 0.5-0.7: 较差的分类能力")
print("  • 0.5: 随机猜测")# 创建可视化图形
fig, axes = plt.subplots(1, 3, figsize=(15, 5))# 4. ROC曲线
plt.sca(axes[0])
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.3f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机分类器')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)', fontsize=12)
plt.ylabel('真正率 (True Positive Rate)', fontsize=12)
plt.title('ROC曲线', fontsize=14, pad=20)
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)# 5. 阈值对指标的影响
plt.sca(axes[1])
test_thresholds = np.arange(0.1, 1.0, 0.1)
precisions = []
recalls = []
f1_scores = []# 演示不同阈值的影响
print(f"\n 不同阈值下的预测结果对比:")
print("阈值 | 精确率 | 召回率 | F1分数")
print("-" * 55)for thresh in test_thresholds:y_pred_thresh = [1 if prob >= thresh else 0 for prob in y_pred_proba]precisions.append(precision_score(y_true, y_pred_thresh, zero_division=0))recalls.append(recall_score(y_true, y_pred_thresh))f1_scores.append(f1_score(y_true, y_pred_thresh, zero_division=0))print(f"{thresh:.1f}  | {precisions[-1]:.3f}  | {recalls[-1]:.3f}  | {f1_scores[-1]:.3f}")plt.plot(test_thresholds, precisions, 'o-', label='精确率', linewidth=2)
plt.plot(test_thresholds, recalls, 's-', label='召回率', linewidth=2)
plt.plot(test_thresholds, f1_scores, '^-', label='F1分数', linewidth=2)
plt.xlabel('分类阈值', fontsize=12)
plt.ylabel('分数', fontsize=12)
plt.title('阈值对指标的影响', fontsize=14, pad=20)
plt.legend()
plt.grid(True, alpha=0.3)print(f"\n 关键洞察:")
print("• 阈值降低 → 召回率↑，精确率↓（更敏感，更多FP）")
print("• 阈值提高 → 精确率↑，召回率↓（更严格，更多FN）")
print("• 需要根据业务需求选择最佳阈值")# 6. 性能总结
plt.sca(axes[2])
plt.axis('off')summary_text = ["*** 模型性能总结 ***","",f"• 准确率: {accuracy_manual:.3f}",f"• 精确率: {precision_manual:.3f}", f"• 召回率: {recall_manual:.3f}",f"• F1分数: {f1_manual:.3f}",f"• AUC: {roc_auc:.3f}","","*** 分析建议: ***",f"• 模型整体准确率: {'良好' if accuracy_manual > 0.7 else '一般'}",f"• 精确率: {'较高' if precision_manual > 0.7 else '需提升'}",f"• 召回率: {'较高' if recall_manual > 0.7 else '需提升'}",f"• 综合性能: {'优秀' if f1_manual > 0.7 else '良好' if f1_manual > 0.5 else '需优化'}"
]for i, text in enumerate(summary_text):plt.text(0.1, 0.9 - i*0.07, text, fontsize=11, verticalalignment='top', transform=plt.gca().transAxes)plt.tight_layout()
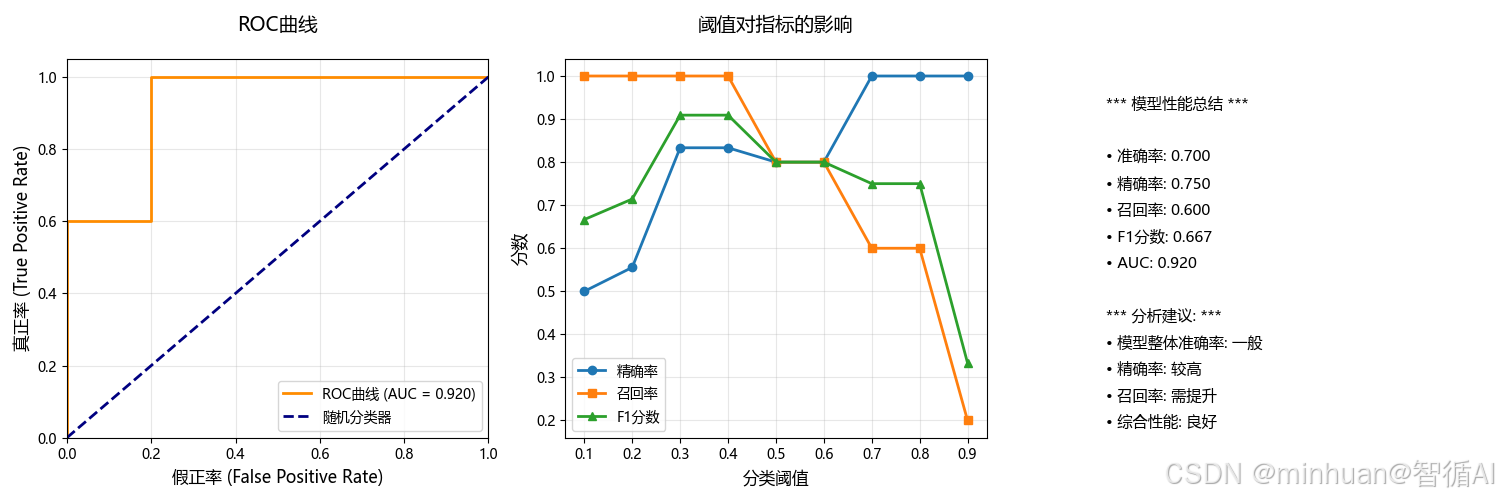
plt.show()

输出结果：

==================================================
ROC曲线与AUC计算:
==================================================

ROC曲线坐标点 (FPR, TPR):
阈值=inf: FPR=0.00, TPR=0.00
阈值=0.90: FPR=0.00, TPR=0.20
阈值=0.80: FPR=0.00, TPR=0.60
阈值=0.70: FPR=0.20, TPR=0.60
阈值=0.40: FPR=0.20, TPR=1.00
阈值=0.10: FPR=1.00, TPR=1.00

AUC (曲线下面积) = 0.920
AUC含义:
• 0.9-1.0: 极好的分类能力
• 0.8-0.9: 良好的分类能力
• 0.7-0.8: 一般的分类能力
• 0.5-0.7: 较差的分类能力
• 0.5: 随机猜测

不同阈值下的预测结果对比:
阈值 | 精确率 | 召回率 | F1分数
-------------------------------------------------------
0.1 | 0.500 | 1.000 | 0.667
0.2 | 0.556 | 1.000 | 0.714
0.3 | 0.833 | 1.000 | 0.909
0.4 | 0.833 | 1.000 | 0.909
0.5 | 0.800 | 0.800 | 0.800
0.6 | 0.800 | 0.800 | 0.800
0.7 | 1.000 | 0.600 | 0.750
0.8 | 1.000 | 0.600 | 0.750
0.9 | 1.000 | 0.200 | 0.333

关键洞察:
• 阈值降低 → 召回率↑，精确率↓（更敏感，更多FP）
• 阈值提高 → 精确率↑，召回率↓（更严格，更多FN）
• 需要根据业务需求选择最佳阈值

阈值的选择：

test_thresholds = np.arange(0.1, 1.0, 0.1)

1. 生成测试范围: 创建从0.1到0.9的阈值序列，步长为0.1
2. 全面评估: 测试模型在不同严格程度下的表现
3. 寻找最优: 帮助找到最适合业务需求的最佳阈值
4. 理解权衡: 展示精确率-召回率之间的trade-off关系
5. 决策支持: 为阈值选择提供数据依据

3. 最佳阈值分析

基于不同阈值下的预测结果对比，阈值0.3或0.4是最好的选择，我们详细分析一下过程：

import matplotlib.pyplot as plt
import numpy as np# 数据
thresholds = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
precisions = [0.500, 0.556, 0.833, 0.833, 0.800, 0.800, 1.000, 1.000, 1.000]
recalls = [1.000, 1.000, 1.000, 1.000, 0.800, 0.800, 0.600, 0.600, 0.200]
f1_scores = [0.667, 0.714, 0.909, 0.909, 0.800, 0.800, 0.750, 0.750, 0.333]# 可视化分析
plt.figure(figsize=(12, 8))plt.plot(thresholds, precisions, 'o-', label='精确率', linewidth=3, markersize=8)
plt.plot(thresholds, recalls, 's-', label='召回率', linewidth=3, markersize=8)
plt.plot(thresholds, f1_scores, '^-', label='F1分数', linewidth=3, markersize=10)# 标记最佳点
best_idx = np.argmax(f1_scores)
plt.axvline(x=thresholds[best_idx], color='red', linestyle='--', alpha=0.7, label=f'最佳阈值 ({thresholds[best_idx]})')
plt.scatter(thresholds[best_idx], f1_scores[best_idx], color='red', s=200, zorder=5)plt.xlabel('分类阈值', fontsize=12)
plt.ylabel('分数', fontsize=12)
plt.title('阈值性能分析 - 最佳阈值选择', fontsize=14, pad=20)
plt.legend()
plt.grid(True, alpha=0.3)
plt.ylim(0, 1.1)# 添加数值标注
for i, (t, p, r, f) in enumerate(zip(thresholds, precisions, recalls, f1_scores)):plt.annotate(f'F1={f:.3f}', (t, f), textcoords="offset points", xytext=(0,10), ha='center', fontsize=9)plt.tight_layout()
plt.show()print(" F1分数排名:")
f1_ranking = sorted(zip(thresholds, f1_scores), key=lambda x: x[1], reverse=True)
for i, (thresh, f1) in enumerate(f1_ranking[:3], 1):print(f"第{i}名: 阈值{thresh} → F1分数 = {f1:.3f}")print("\n 不同业务场景下的最佳选择:")
print("=" * 50)scenarios = {"疾病筛查": {"priority": "召回率", "recommended": [0.3, 0.4], "reason": "不能漏掉任何患者"},"垃圾邮件过滤": {"priority": "精确率", "recommended": [0.7, 0.8], "reason": "不能误判重要邮件"}, "平衡场景": {"priority": "F1分数", "recommended": [0.3, 0.4], "reason": "精确率和召回率都很好"},"欺诈检测": {"priority": "召回率", "recommended": [0.3, 0.4], "reason": "不能漏掉欺诈交易"}
}for scenario, info in scenarios.items():print(f" {scenario}:")print(f"   关注指标: {info['priority']}")print(f"   推荐阈值: {info['recommended']}")print(f"   原因: {info['reason']}")print()# 创建详细比较表
print(" 前三名阈值详细比较:")
print("阈值 | 精确率 | 召回率 | F1分数 | 优势")
print("-" * 55)top_thresholds = [(0.3, 0.833, 1.000, 0.909),(0.4, 0.833, 1.000, 0.909), (0.5, 0.800, 0.800, 0.800)]for thresh, prec, rec, f1 in top_thresholds:if thresh in [0.3, 0.4]:advantage = " 完美召回率 + 高精确率"else:advantage = " 平衡但两者都不突出"print(f"{thresh}   | {prec:.3f}   | {rec:.3f}  | {f1:.3f}  | {advantage}")

输出结果：

F1分数排名:
第1名: 阈值0.3 → F1分数 = 0.909
第2名: 阈值0.4 → F1分数 = 0.909
第3名: 阈值0.5 → F1分数 = 0.800

不同业务场景下的最佳选择:
==================================================
疾病筛查:
关注指标: 召回率
推荐阈值: [0.3, 0.4]
原因: 不能漏掉任何患者

垃圾邮件过滤:
关注指标: 精确率
推荐阈值: [0.7, 0.8]
原因: 不能误判重要邮件

平衡场景:
关注指标: F1分数
推荐阈值: [0.3, 0.4]
原因: 精确率和召回率都很好

欺诈检测:
关注指标: 召回率
推荐阈值: [0.3, 0.4]
原因: 不能漏掉欺诈交易

前三名阈值详细比较:
阈值 | 精确率 | 召回率 | F1分数 | 优势
-------------------------------------------------------
0.3 | 0.833 | 1.000 | 0.909 | 完美召回率 + 高精确率
0.4 | 0.833 | 1.000 | 0.909 | 完美召回率 + 高精确率
0.5 | 0.800 | 0.800 | 0.800 | 平衡但两者都不突出

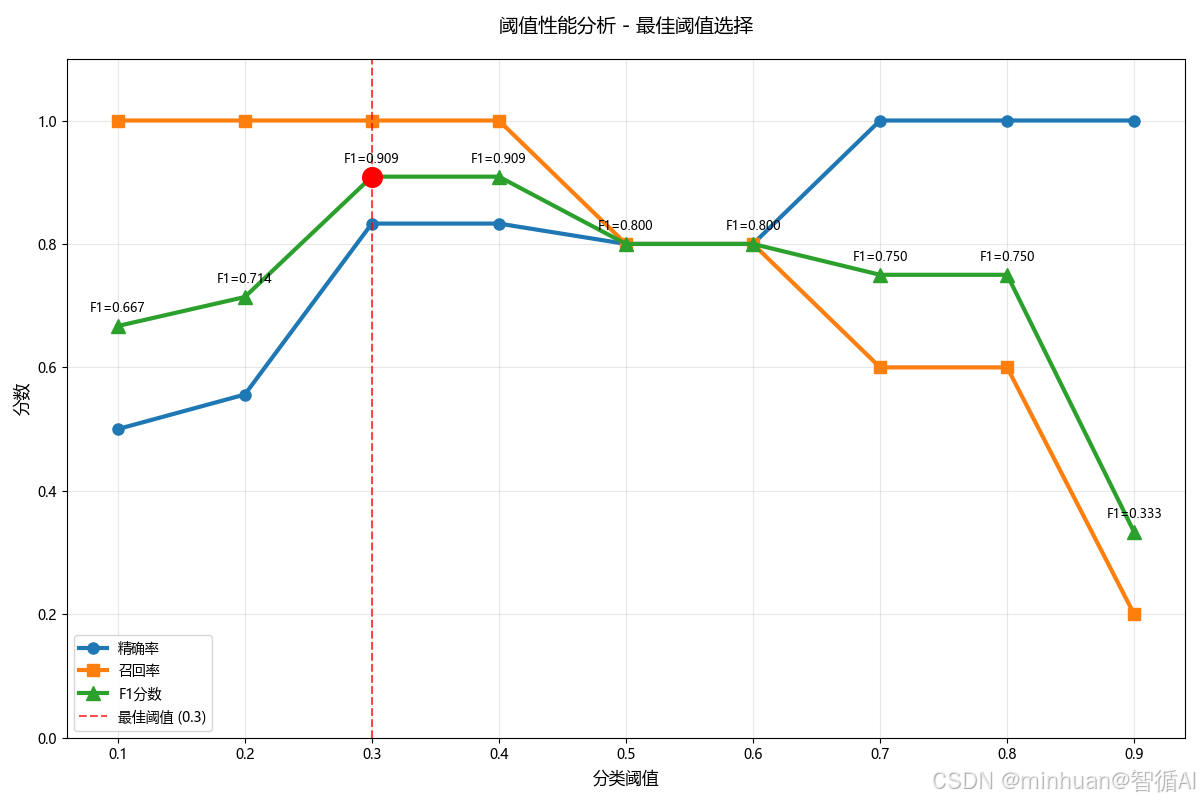
阈值0.3/0.4的优势：

1. 完美的召回率 (1.000)
- 能够找出所有的真实正例
- 没有漏报(FN)
- 对于不能接受漏报的场景至关重要
2. 很高的精确率 (0.833)
- 当模型预测为正例时，83.3%的概率是正确的
- 只有16.7%的误报率
3. 最优的F1分数 (0.909)
- 在精确率和召回率之间达到最佳平衡
- 是所有阈值中最高的综合分数

其他阈值的问题：

阈值0.1-0.2：精确率太低 (50%-55%)，误报太多
阈值0.5-0.6：召回率下降至80%，开始出现漏报
阈值0.7-0.8：召回率大幅下降至60%，漏报严重
阈值0.9：召回率只有20%，基本无法找出正例

阈值0.3和0.4在保持完美召回率的同时，提供了很高的精确率，达到了精确率-召回率权衡的最佳平衡点，因此是最佳选择。

四、指标的适用性与选择

选择评估指标的本质，是将技术指标与业务目标对齐。以下是一些常见场景的策略：

1. 均衡数据，无特殊业务偏好

推荐指标：准确率、F1分数、AUC。
场景：MNIST手写数字识别。我们希望整体识别正确率越高越好。

2. 高度关注误报，追求宁缺毋滥

核心指标：精确率。
场景：
- 推荐系统：向用户推送的内容必须高度相关，不相关的推荐（FP）会损害用户体验。
- 垃圾邮件过滤：将正常邮件误判为垃圾邮件（FP）的代价很高。

3. 高度关注漏报，追求“宁可错杀，不可放过”

核心指标：召回率。
场景：
- 疾病筛查：漏掉一个病人（FN）的后果远比让一个健康人做进一步检查（FP）更严重。
- 金融风控：漏掉一个欺诈交易（FN）可能导致直接的经济损失。

4. 需要在精确率和召回率之间取得平衡

核心指标：F1分数。
场景：
- 学术论文的查重系统：既不能过于宽松（召回率低，漏掉抄袭），也不能过于严苛（精确率低，误伤原创）。
- 电商评论的情感分析：需要平衡正面和负面评论的识别。

5. 需要全面评估模型整体排序性能，或数据高度不平衡

核心指标：ROC曲线与AUC。
场景：
- 任何不平衡分类问题，如欺诈检测、客户流失预测、罕见病诊断等。AUC能给出一个稳健的性能评估。
- 当你不确定如何设定分类阈值时，ROC曲线可以帮你分析不同阈值下的模型表现，为最终决策提供依据。

6. 当误分类的代价不对称时

核心指标：代价敏感分析或指定业务目标下的Fβ分数。
说明：F1分数是Fβ分数在β=1时的特例。Fβ = (1+β²) * (Precision * Recall) / (β² * Precision + Recall)。
- 如果认为召回率更重要，就设置β>1（例如，F2分数）。
- 如果认为精确率更重要，就设置β<1（例如，F0.5分数）。