构建AI智能体:七十、小树成林,聚沙成塔:随机森林与大模型的协同进化
一. 什么是随机森林
随机森林是一种非常强大的机器学习算法,它属于集成学习中的Bagging方法。随机森林的基本单元是决策树,而森林就是由很多棵决策树组成的。简单的说随机森林就是由多个决策树组成的森林,每棵树都是一个独立的预测模型。通过集体投票或平均意见来做出最终决策,这样比单棵决策树更准确、更稳定。
随机森林的核心思想是:通过构建多个决策树,并将它们的预测结果结合起来,从而获得比单个决策树更准确、更稳定的预测。
随机森林的重要性:
- 它能够处理大规模的数据集,并且具有很高的准确性。
- 它能够处理高维数据,并且不需要降维。
- 它能够评估各个特征的重要性。
- 它不容易过拟合,因为多棵树进行了平均。
二、决策树回顾
决策树是随机森林的基本单元,前期文章《构建AI智能体:三十五、决策树的核心机制(一):刨根问底鸢尾花分类中的参数推理计算》,我们详细探讨了决策树的细节内容,如不清楚建议先了解,简单来说决策树是一种模拟人类决策过程的模型,它通过一系列的问题对数据进行分割,直到得到最终的决策。例如,我们定是否外出,我们会先看看天气如何:如果是晴天,在看看看气温,如果温度大于25°C ,那么我们考虑去游泳,如果温度不到25°C,那么我们可能考虑去爬山,如果天气是下雨的,那么我们就选择不出门,在家看书。
1. 决策树是什么
决策树就像我们做决策时的思考过程。比如决定是否外出:
今天天气如何?
├── 晴天 → 温度如何?
│ ├── 温度 > 25°C → 去游泳
│ └── 温度 ≤ 25°C → 去爬山
└── 下雨 → 在家看书
2. 简单的决策树示例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier, plot_treeplt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 创建示例数据
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1, random_state=42)# 训练决策树
tree = DecisionTreeClassifier(max_depth=3, random_state=42)
tree.fit(X, y)# 可视化决策树
plt.figure(figsize=(12, 8))
plot_tree(tree, filled=True, feature_names=['特征1', '特征2'], class_names=['类别0', '类别1'])
plt.title('决策树结构')
plt.show()代码详解:
- make_classification:生成分类数据集
- DecisionTreeClassifier:决策树分类器
- max_depth=3:限制树深度,防止过拟合
- plot_tree:可视化决策树结构
输出结果:
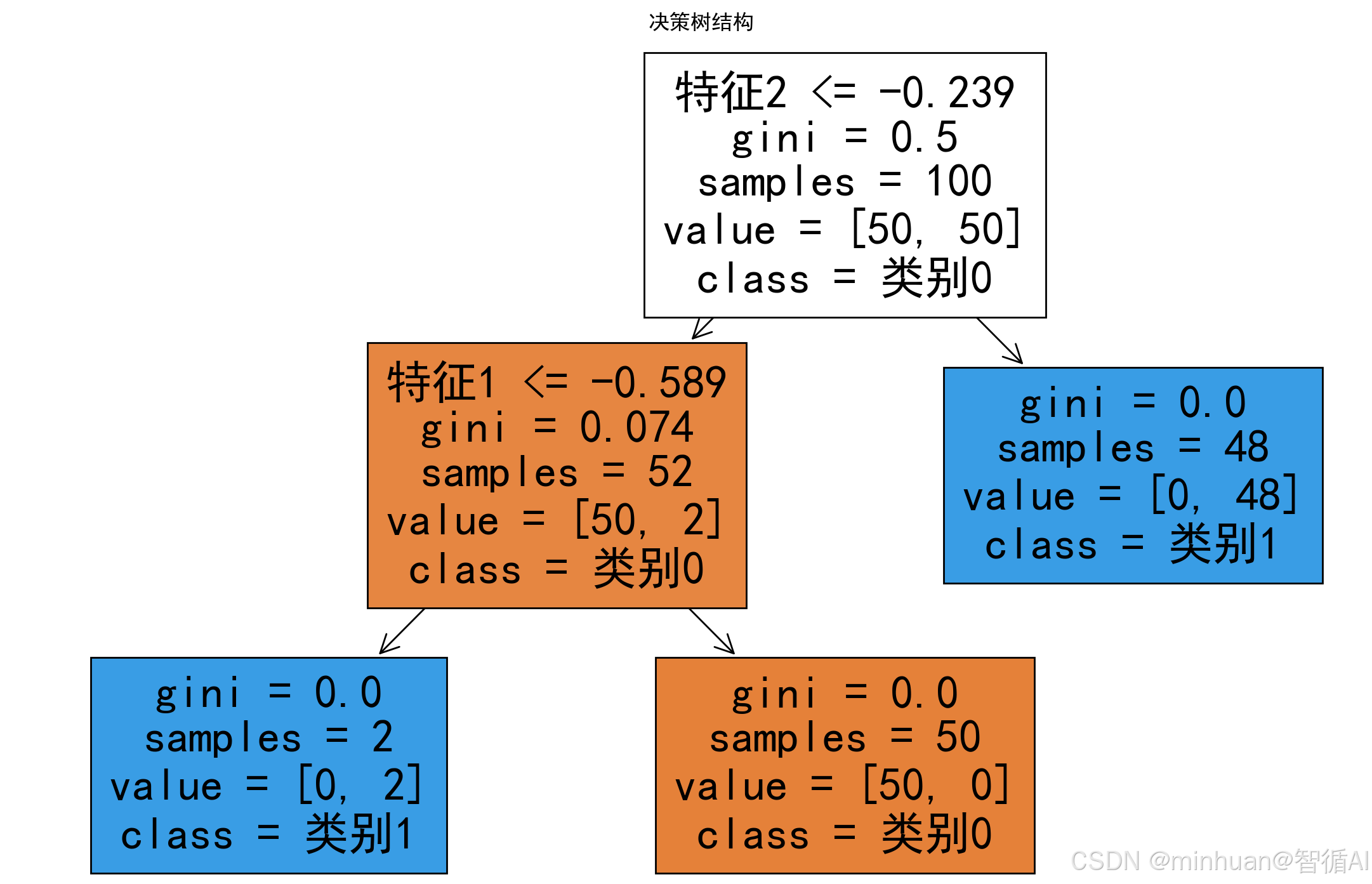
3. 决策树如何做决策
决策树通过递归分割数据来学习,其生成过程包括特征选择、树的构建和剪枝。在特征选择中,关键问题是:如何选择最佳分割点?通常使用信息增益、基尼指数等指标,其目标是选择能让数据变得"最纯净"的分割方式。
from collections import Counter
import math
import numpy as npdef calculate_entropy(labels):"""计算信息熵"""counter = Counter(labels)total = len(labels)entropy = 0.0for count in counter.values():probability = count / totalentropy -= probability * math.log2(probability)return entropydef calculate_information_gain(data, labels, feature_index, threshold):"""计算信息增益"""# 保证 labels 为 numpy 数组,便于布尔索引labels_np = np.asarray(labels)# 分割数据left_mask = data[:, feature_index] <= thresholdright_mask = ~left_maskleft_labels = labels_np[left_mask]right_labels = labels_np[right_mask]# 计算父节点熵parent_entropy = calculate_entropy(labels_np)# 计算子节点加权平均熵n_left, n_right, n_total = len(left_labels), len(right_labels), len(labels_np)children_entropy = (n_left / n_total) * calculate_entropy(left_labels) + \(n_right / n_total) * calculate_entropy(right_labels)# 信息增益 = 父节点熵 - 子节点加权平均熵return parent_entropy - children_entropy# 示例:计算不同分割点的信息增益
print("信息熵计算示例:")
sample_labels = [0, 0, 0, 1, 1, 1]
print(f"样本标签: {sample_labels}")
print(f"信息熵: {calculate_entropy(sample_labels):.4f}")# 测试不同分割
test_data = np.array([[1], [2], [3], [4], [5], [6]])
test_labels = [0, 0, 0, 1, 1, 1]for threshold in [2.5, 3.5, 4.5]:gain = calculate_information_gain(test_data, test_labels, 0, threshold)print(f"阈值 {threshold} 的信息增益: {gain:.4f}")推理过程:
- 计算当前节点的混乱程度(信息熵)
- 尝试不同的分割方式
- 选择信息增益最大的分割方式
- 递归应用到每个子节点
输出结果:
信息熵计算示例:
样本标签: [0, 0, 0, 1, 1, 1]
信息熵: 1.0000
阈值 2.5 的信息增益: 0.4591
阈值 3.5 的信息增益: 1.0000
阈值 4.5 的信息增益: 0.4591
决策树涉及的相关概念参考:
- 信息熵、信息增益:《信息论完全指南:从基础概念到在大模型中的实际应用》
- 最佳分割点、基尼指数:《决策树的核心机制(二):抽丝剥茧简化专业术语推理最佳分裂点》
三、集成学习回顾
集成学习的核心思想在于群体智慧,其“从一棵树到一片森林”的构建范式,形象地揭示了这一理念:通过构建大量存在差异的决策树,形成一个规模庞大的模型集合(森林)。在预测时,这片“森林”并非依赖其中任何单一树木的判断,而是通过集体投票或平均来做出最终决策,从而有效规避单棵树的个体偏见与不稳定性,汇聚为更强大、更稳健的预测能力。
集成学习通过组合多个学习器来获得比单一学习器更好的性能。随机森林属于集成学习中的Bagging方法。
Bagging的基本思想是:
- 从原始数据集中有放回地随机抽取多个样本子集(bootstrap样本)。
- 在每个样本子集上训练一个基学习器(比如决策树)。
- 将这些基学习器的预测结果进行组合(分类问题使用投票,回归问题使用平均)。
随机森林在Bagging的基础上又进了一步:不仅在数据上进行随机抽样,而且在训练每棵树时,对特征也进行随机选择。这样进一步增加了树的多样性,从而提升模型的泛化能力。详细内容可参考《六十八、集成学习:从三个臭皮匠到AI集体智慧的深度解析》。
四、随机森林原理解析
1. 随机森林的核心思想
随机森林通过两个随机性来增强多样性:
1.1 Bootstrap采样:每棵树用不同的训练子集
Bootstrap采样是一种统计学方法,它的核心思想是“以小见大,通过模拟逼近真实”,即在只有一份样本的情况下,通过对原始数据集进行有放回的随机抽样,这个过程重复多次,从而得到多个Bootstrap样本。然后,我们可以基于这些Bootstrap样本估计统计量(如均值、方差、中位数等)的抽样分布。这种方法特别适用于小样本数据集,能够有效估计统计量的分布和不确定性。
Bootstrap采样的步骤:
- 1. 从原始数据集中随机抽取一个样本,并记录。
- 2. 将该样本放回原始数据集,使得下次抽样时该样本仍有可能被抽到。
- 3. 重复步骤1和2,直到抽取的样本数量达到原始数据集的样本数n。这样就得到了一个Bootstrap样本。
- 4. 重复上述过程B次(例如B=1000),得到B个Bootstrap样本。
每个Bootstrap样本与原始数据集的大小相同,但由于是有放回抽样,每个Bootstrap样本中有些样本会出现多次,而有些样本则不会出现。
1.2 特征随机选择:每棵树分裂时只考虑部分特征
特征随机选择是指在模型训练过程中,随机地选取一部分特征来进行学习,而不是每次都使用全部的特征。在模型训练的每个步骤中,随机限制可用的特征,迫使模型学习更鲁棒、更多样的规则。
目标:通过降低模型间的相关性来减少方差,防止过拟合。
核心思想与作用:
- 打破模型的惯性:如果模型在每一轮训练(例如决策树的每一个节点分裂)中都考虑所有特征,那么那些强度最高、最显著的特征会始终被选中。这会导致所有生成的树或模型都非常相似,即模型之间具有高度的相关性。高度相关的模型集成起来,方差减少的效果有限。
- 引入随机性,降低方差:通过强制模型只关注特征的一个随机子集,我们迫使它去探索那些在全局看来可能不那么显著,但在特定局部情境下非常有用的特征。这相当于给模型增加了“扰动”。
- 提升泛化能力:由于模型不再过度依赖少数几个强特征,它学到的规则会更加多样和鲁棒,从而在面对新数据时表现更好。
- 提高训练效率:在每一个节点上,只需要在特征的一个子集中寻找最佳分裂点,计算量会显著降低。
在随机森林中的工作流程:
- 1. 从原始数据集中使用Bootstrap抽样方法,有放回地抽取多个样本子集。
- 2. 为每一个样本子集训练一棵决策树。
- 3. 在训练每棵树的每一个节点进行分裂时:
- 不再从所有 M 个特征中选择最佳分裂特征。
- 而是首先从所有特征中随机选取一个特征子集(假设大小为 m,通常 m = sqrt(M) 或 log2(M))。
- 然后仅在这个小的随机特征子集中寻找最佳分裂特征和分裂点。
- 4. 重复这个过程,直到树生长到预定的深度或满足停止条件。
- 5. 将森林中所有树的预测结果进行集成(分类问题用投票,回归问题用平均)。
特征随机的优势:
集成的“群体智慧”要发挥作用,其基础是个体模型必须具备多样性。如果所有模型都一样,那集成毫无意义。特征随机选择正是为了刻意地创造模型之间的多样性,多样性决定集成效果。
- 没有特征随机选择:所有树都会在全局最优的几个特征上分裂,导致树的结构非常相似。模型方差降低有限。
- 有特征随机选择:每棵树可能在不同的特征子集上分裂,从而生长出结构迥异的树。这些多样化的模型从不同角度学习数据,它们的错误互不相关,集成后能显著降低整体模型的方差,提升泛化性能。
2. 随机森林的流程图
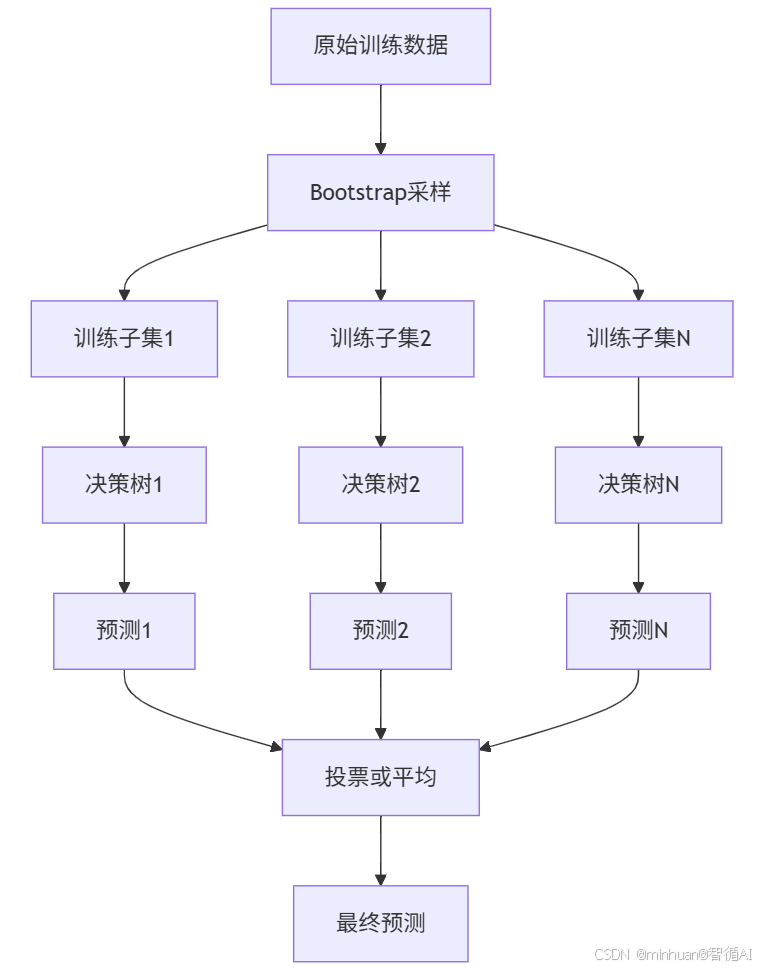
随机森林的构建过程:
- 1. 从原始训练集中使用Bootstrap方法随机有放回地抽取n个样本,作为一棵树的训练集。
- 2. 对于每棵树,从所有特征中随机选择m个特征(m通常远小于总特征数),然后从这m个特征中选择最佳分割点来分裂节点。
- 3. 每棵树都尽可能生长,不进行剪枝(或者使用最小剪枝)。
- 4. 重复步骤1-3,直到生成指定数量的树。
3. Bootstrap采样详解
import numpy as npdef bootstrap_sampling(data, labels, n_trees=3):"""Bootstrap采样实现"""n_samples = len(data)bootstrap_datasets = []for i in range(n_trees):# 有放回随机采样indices = np.random.choice(n_samples, n_samples, replace=True)bootstrap_data = data[indices]bootstrap_labels = labels[indices]bootstrap_datasets.append((bootstrap_data, bootstrap_labels))print(f"树{i+1}的采样结果:")print(f" 采样索引: {indices}")print(f" 唯一样本数: {len(np.unique(indices))}/{n_samples}")print()return bootstrap_datasets# 示例数据
simple_data = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
simple_labels = np.array([0, 1, 0, 1])bootstrap_datasets = bootstrap_sampling(simple_data, simple_labels)输出结果:
树1的采样结果:
采样索引: [0 1 1 3]
唯一样本数: 3/4树2的采样结果:
采样索引: [3 2 0 1]
唯一样本数: 4/4树3的采样结果:
采样索引: [2 3 3 0]
唯一样本数: 3/4
关键概念:有放回抽样
- 代码中的 replace=True 表示抽样后会把样本放回,同一个样本可能被多次抽中
- 从4个样本中抽取4次,可能产生重复样本
采样过程分析:
- 第一次采样(树1):
- 第一次随机生成的索引是:[0, 1, 1, 3]
- 采样结果分析:
- 索引0: 选择第1个样本 [1, 2],标签 0
- 索引1: 选择第2个样本 [3, 4],标签 1
- 索引1: 再次选择第2个样本 [3, 4],标签 1(重复!)
- 索引3: 选择第4个样本 [7, 8],标签 1
- 唯一样本数:3/4
- 实际使用了4个样本位置,但只有3个不同的原始样本
- 样本 [3, 4] 被使用了2次
- 样本 [5, 6] 完全没有被选中
- 第二次采样(树2):
- 第二次随机生成的索引是:[3, 2, 0, 1]
- 采样结果分析:
- 所有4个不同的样本都被选中一次
- 没有重复样本
- 唯一样本数:4/4 - 这是可能的,但不常见
- 第三次采样(树3):
- 第三次随机生成的索引是:[2, 3, 3, 0]
- 采样结果分析:
- 索引2: 选择第3个样本 [5, 6],标签 0
- 索引3: 选择第4个样本 [7, 8],标签 1
- 索引3: 再次选择第4个样本 [7, 8],标签 1(重复!)
- 索引0: 选择第1个样本 [1, 2],标签 0
- 唯一样本数:3/4
- 样本 [7, 8] 被使用了2次
- 样本 [3, 4] 没有被选中
4. 特征随机选择
import numpy as npdef feature_sampling(features, max_features='sqrt'):"""特征随机选择"""n_features = len(features)if max_features == 'sqrt':n_select = int(np.sqrt(n_features))elif max_features == 'log2':n_select = int(np.log2(n_features))else:n_select = max_featuresselected_indices = np.random.choice(n_features, n_select, replace=False)selected_features = [features[i] for i in selected_indices]return selected_indices, selected_features# 示例
features = ['年龄', '工资', '学历', '工作经验', '城市', '性别', '婚姻状况']
print("所有特征:", features)selected_indices, selected_features = feature_sampling(features, 'sqrt')
print(f"随机选择的特征索引: {selected_indices}")
print(f"随机选择的特征: {selected_features}")输出结果:
所有特征: ['年龄', '工资', '学历', '工作经验', '城市', '性别', '婚姻状况']
随机选择的特征索引: [2 5]
随机选择的特征: ['学历', '性别']
特征选择策略:
- 总特征数:7个
- 使用 'sqrt' 策略:n_select = int(np.sqrt(7)) ≈ int(2.645) = 2 ,每次随机选择 2个特征
- 使用 'log2' 策略:n_select = int(np.log2(7)) ≈ int(2.807) = 2 ,每次随机选择 2个特征
五、随机森林的超参数
超参数是机器学习模型在训练开始前需要设定的配置参数,它们不是从数据中学习得到的,而是用来控制学习过程的指导参数,通俗的理解,想象一下,我们在骑自行车时,需要先进行一些调整,比如座椅高度、把手位置和轮胎气压。这些设置不是我们在骑行过程中自动学会的,而是我们在开始前手动调整的。超参数就像这些设置,它们是机器学习模型在训练开始前,由我们人工设定的参数,用来控制模型如何学习。
建议看本小节务必先了解超参数基本原理:《六十七、超参数如何影响大模型?通俗讲解原理、作用与实战示例》
随机森林有一些重要的超参数,例如:
- n_estimators:森林中树的数量。
- max_features:每棵树分裂时考虑的最大特征数。
- max_depth:树的最大深度。
- min_samples_split:内部节点再划分所需最小样本数。
- min_samples_leaf:叶子节点最少样本数。
调整这些超参数可以优化模型性能。
1. 示例代码
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 加载乳腺癌数据集
data = load_breast_cancer()
X, y = data.data, data.target
feature_names = data.feature_namesprint("数据集信息:")
print(f"特征数量: {X.shape[1]}")
print(f"样本数量: {X.shape[0]}")
print(f"类别分布: {np.bincount(y)}")# 划分训练测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建随机森林
rf = RandomForestClassifier(n_estimators=100, # 树的数量max_depth=10, # 最大深度min_samples_split=2, # 内部节点再划分所需最小样本数min_samples_leaf=1, # 叶节点最少样本数max_features='sqrt', # 特征选择方式random_state=42,n_jobs=-1 # 使用所有CPU核心
)# 训练模型
rf.fit(X_train, y_train)# 预测
y_pred = rf.predict(X_test)
y_pred_proba = rf.predict_proba(X_test)# 评估模型
print("\n=== 模型评估 ===")
print(f"训练集准确率: {rf.score(X_train, y_train):.4f}")
print(f"测试集准确率: {rf.score(X_test, y_test):.4f}")# 交叉验证
cv_scores = cross_val_score(rf, X, y, cv=5)
print(f"交叉验证准确率: {cv_scores.mean():.4f} (±{cv_scores.std() * 2:.4f})")# 详细分类报告
print("\n分类报告:")
print(classification_report(y_test, y_pred, target_names=data.target_names))# 混淆矩阵
plt.figure(figsize=(8, 6))
cm = confusion_matrix(y_test, y_pred)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=data.target_names, yticklabels=data.target_names)
plt.title('混淆矩阵')
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.show()# 定义参数网格
param_grid = {'n_estimators': [50, 100, 200],'max_depth': [5, 10, 15, None],'min_samples_split': [2, 5, 10],'min_samples_leaf': [1, 2, 4],'max_features': ['sqrt', 'log2']
}# 网格搜索
grid_search = GridSearchCV(RandomForestClassifier(random_state=42),param_grid,cv=5,scoring='accuracy',n_jobs=-1,verbose=1
)# 简化版参数调优
simple_param_grid = {'n_estimators': [50, 100],'max_depth': [5, 10]
}simple_search = GridSearchCV(RandomForestClassifier(random_state=42),simple_param_grid,cv=3,scoring='accuracy',n_jobs=-1
)simple_search.fit(X_train, y_train)print("简化调优最佳参数:", simple_search.best_params_)
print("简化调优最佳分数:", simple_search.best_score_)2. 代码分析
2.1 参数调优的核心:GridSearchCV
网格搜索是一种穷举式的参数调优方法:
- 定义参数的候选值范围
- 尝试所有可能的参数组合
- 通过交叉验证评估每个组合的性能
- 选择最佳性能的参数组合
代码中的参数网格:
simple_param_grid = {'n_estimators': [50, 100], # 树的数量'max_depth': [5, 10], # 树的最大深度
}- 参数组合数:2 × 2 = 4种组合
- 总训练次数:4 × 3折 = 12次模型训练
参数的意义:
- n_estimators(树的数量)
- 值小:训练快,但可能欠拟合
- 值大:效果更好,但计算成本高
- 平衡点:通常100-200之间
- max_depth(树的最大深度)
- 值小:树简单,防止过拟合,但可能欠拟合
- 值大/None:树复杂,可能过拟合
- 经验值:5-15之间
3. 输出结果
数据集信息:
特征数量: 30
样本数量: 569
类别分布: [212 357]=== 模型评估 ===
训练集准确率: 1.0000
测试集准确率: 0.9708
交叉验证准确率: 0.9561 (±0.0457)分类报告:
precision recall f1-score supportmalignant 0.98 0.94 0.96 63
benign 0.96 0.99 0.98 108accuracy 0.97 171
macro avg 0.97 0.96 0.97 171
weighted avg 0.97 0.97 0.97 171简化调优最佳参数: {'max_depth': 10, 'n_estimators': 50}
简化调优最佳分数: 0.9622920938710413
4. 运行流程

5. 结果说明
分类报告:
precision recall f1-score supportmalignant 0.98 0.94 0.96 63
benign 0.96 0.99 0.98 108accuracy 0.97 171
macro avg 0.97 0.96 0.97 171
weighted avg 0.97 0.97 0.97 171简化调优最佳参数: {'max_depth': 10, 'n_estimators': 50}
简化调优最佳分数: 0.9622920938710413
这表示:
- 在测试的参数组合中,max_depth=10和n_estimators=100表现最好
- 通过3折交叉验证的平均准确率为96.5%
5.1 分类报告详解
数据集信息:
- 类别1: malignant(恶性) - 63个样本
- 类别2: benign(良性) - 108个样本
- 总样本数: 171个测试样本
- 准确率: 0.97 (97%)
核心指标详解:
Precision(精确率/查准率)
- 问题:当模型预测为某个类别时,有多大概率是正确的?
- 计算公式:Precision = TP / (TP + FP)
- malignant: 0.98 - 当模型预测为恶性时,98%的情况是正确的
- benign: 0.96 - 当模型预测为良性时,96%的情况是正确的
Recall(召回率/查全率)
- 问题:实际为某个类别的样本中,模型能找出多少?
- 计算公式:Recall = TP / (TP + FN)
- malignant: 0.94 - 实际为恶性的样本中,模型找出了94%
- benign: 0.99 - 实际为良性的样本中,模型找出了99%
F1-Score(F1分数)
- Precision和Recall的调和平均数
- 计算公式:F1 = 2 × (Precision × Recall) / (Precision + Recall)
- 综合平衡精确率和召回率
- malignant: 0.96
- benign: 0.98
混淆矩阵推理:
根据这些指标,我们可以推断出混淆矩阵:
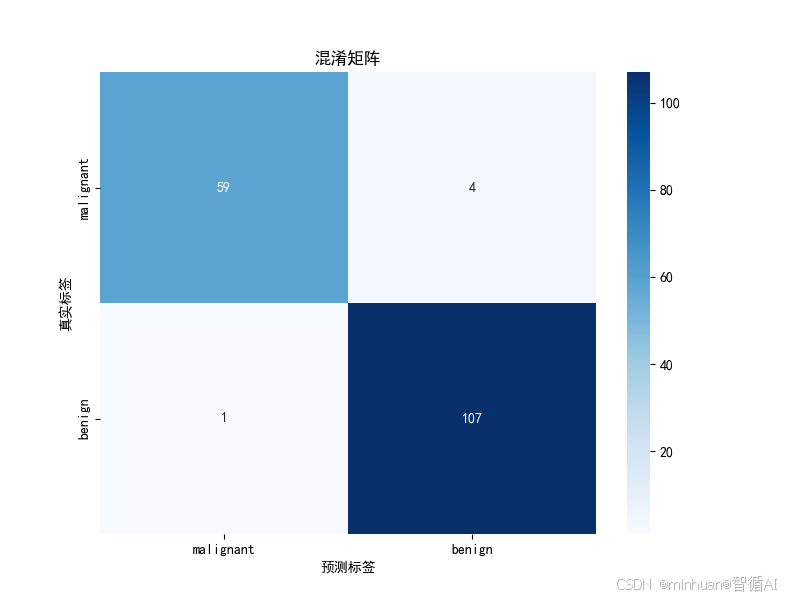
- 实际恶性(63) → 预测恶性: 59个, 预测良性: 4个
- 实际良性(108) → 预测良性: 107个, 预测恶性: 1个
计算验证:
- malignant recall = 59/63 ≈ 0.94 ✓
- benign recall = 107/108 ≈ 0.99 ✓
- malignant precision = 59/(59+1) = 59/60 ≈ 0.98 ✓
- benign precision = 107/(107+4) = 107/111 ≈ 0.96 ✓
平均值说明:
macro avg(宏平均)
- precision:(0.98 + 0.96)/2 = 0.97
- recall:(0.94 + 0.99)/2 = 0.965
- 特点:平等看待每个类别,不考虑样本数量差异
weighted avg(加权平均)
- precision:(0.98*63 + 0.96*108)/171 ≈ 0.97
- recall:(0.94*63 + 0.99*108)/171 ≈ 0.97
- 特点:按样本数量加权,更反映整体性能
六、总结
随机森林是一种强大的集成学习算法,其核心思想是通过构建众多决策树,并以集体投票或平均的方式作出最终预测,从而显著提升模型的泛化能力和鲁棒性。
该算法的成功关键在于引入两大随机性:在数据层面使用Bootstrap采样为每棵树构建略有差异的训练集,同时在特征层面进行随机选择,这种机制确保了树与树之间的差异性,有效避免了过拟合。
与许多复杂模型相比,随机森林具有显著的工程化优势,它无需复杂的特征进行归一化缩放,能原生处理混合数据类型,并且其训练过程高度并行化。这些特性使其在工业界的大规模数据场景下,成为一个非常可靠、易于部署和维护的基石模型。
