当前位置： 首页 > news >正文

从零实现 vLLM (1.2）：如何实现张量并行

news 2025/10/22 11:35:11

前言

在上篇文章《从零实现 vLLM (1.1）：并行词嵌入 VocabParallelEmbedding》中，我们分析了 Qwen3Model 模型中第一个组件：VocabParallelEmbedding 的源码。今天这篇文章我们深入到 Qwen3DecoderLayer 的第一个核心组件：Qwen3Attention，重点分析 QKVParallelLinear 和 RowParallelLinear，这里涉及了推理引擎的核心概念：张量并行。

张量并行（Tensor Parallelism）在大模型推理引擎中至关重要，可以说是核心技术之一。

原因主要有两点：

  1. 解决单张 GPU 显存不足的问题：现在的大模型（比如拥有几百上千亿参数的模型）的权重矩阵非常巨大，单张 GPU 根本放不下。张量并行通过将这些巨大的权重矩阵（比如线性层中的权重）切分到多张 GPU 上，使得模型能够被成功加载和运行。ColumnParallelLinear（列并行）和 RowParallelLinear（行并行）就是将一个大的矩阵运算拆分给多个 GPU 协同完成。

  2. 实现计算加速：张量并行不仅解决了存储问题，还能将计算任务（主要是矩阵乘法）也分配到多个 GPU 上同时执行，从而显著提升推理速度。文中 NumPy 的示例清晰地展示了，如何将计算任务分配到两个模拟的 GPU 上，并通过 All-Reduce 等通信操作最终得到和单 GPU 一样的正确结果，但过程是并行的。

总而言之，没有张量并行技术，我们就无法在现有的硬件上高效地运行那些参数量巨大的模型。它是支撑大模型从训练走向实际应用（推理）的关键基石。

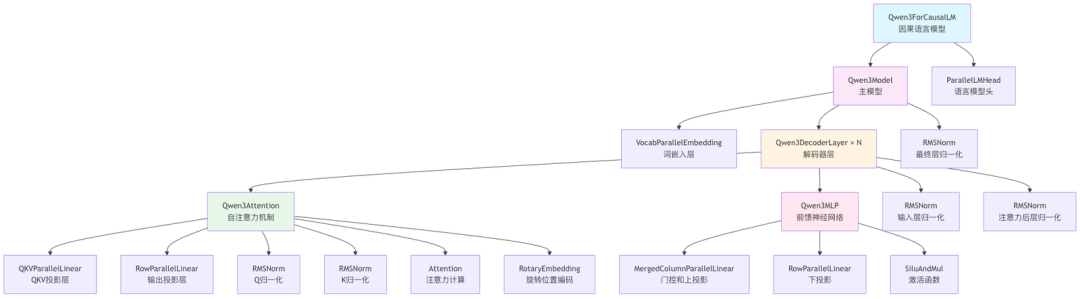
Qwen3Attention 的核心组件如下图所示，我们分析前面两个组件：QKVParallelLinear 和 RowParallelLinear。

Qwen3Attention (继承自 nn.Module)
├── qkv_proj: QKVParallelLinear (用于合并计算 Q, K, V)
│   └── (继承自) ColumnParallelLinear (列并行层)
│       └── (继承自) LinearBase (并行层抽象基类)
│
├── o_proj: RowParallelLinear (用于 Attention 输出)
│   └── (继承自) LinearBase (并行层抽象基类)
│
├── rotary_emb: RotaryEmbedding (旋转位置编码)
│
├── attn: Attention (底层 Attention 计算核心)
│   └── (使用) Context (用于获取 prefill/decode 状态及相关参数)
│
├── q_norm: RMSNorm (对 Query 向量进行归一化)
│
└── k_norm: RMSNorm (对 Key 向量进行归一化)

GPU 张量并行计算过程详解：代码与结果分析

张量并行就是将线性代数中的矩阵运算规则，巧妙地应用于分布式计算中。通过线性代数中的矩阵分块和乘法法则，拆解成可以在多个设备上独立执行的小任务，最后再通过特定的通信操作将结果聚合，从而实现加速。

下面通过一个具体的例子，逐步演示张量并行技术中“列并行”和“行并行”的计算过程。我们将首先在模拟的单个设备上进行标准矩阵乘法作为基准，然后模拟在两个 GPU 上并行计算，并验证结果的一致性。

一、 环境设置与数据准备

首先，我们设置计算环境，定义矩阵维度，并创建模拟数据。

代码:

import numpy as np# 设置随机种子以保证每次运行结果都一样，方便验证
np.random.seed(42)
# 设置numpy的打印选项，让输出更整洁（不使用科学计数法）
np.set_printoptions(suppress=True)# 模拟有 2 个 GPU
gpu_count = 2# 定义矩阵维度
seq_len = 2      # 序列长度
input_dim = 2    # 输入特征维度
hidden_dim = 4   # 隐藏层维度, 设为4方便2个GPU平分
output_dim = 2   # MLP后输出维度# 创建随机整数矩阵来模拟输入和权重
input_activations = np.random.randint(1, 10, size=(seq_len, input_dim))
weights_A = np.random.randint(1, 10, size=(input_dim, hidden_dim))
weights_B = np.random.randint(1, 10, size=(hidden_dim, output_dim))

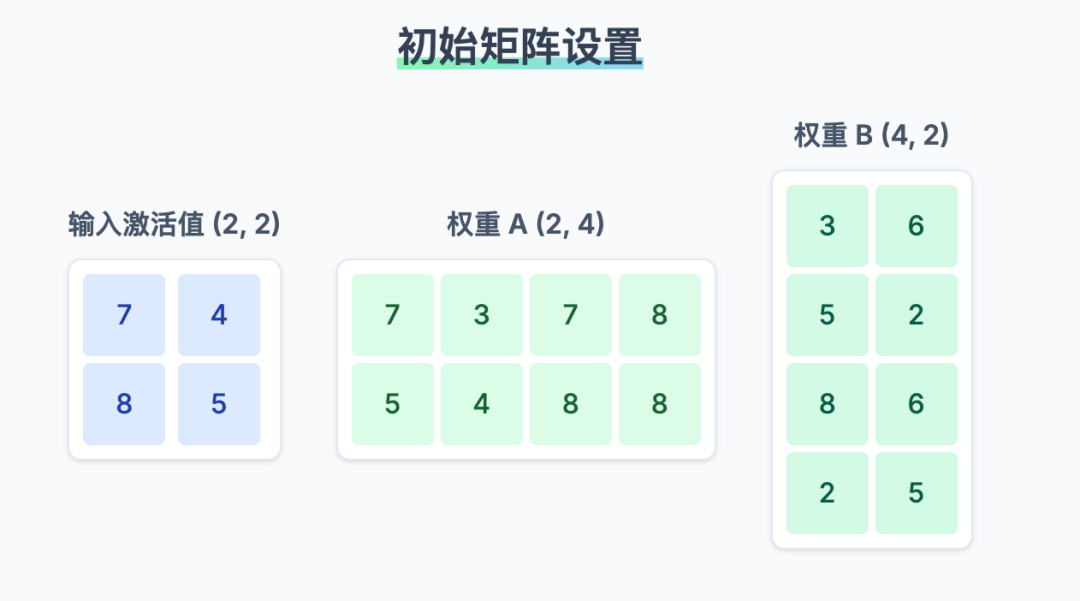
我们导入 numpy 库用于科学计算。通过设置固定的随机种子，确保每次生成的随机矩阵都是相同的，便于复现和验证。我们定义了本次模拟的场景：2个GPU，输入矩阵 X 的维度为 (2, 2)，第一个权重矩阵 A 的维度为 (2, 4)，第二个权重矩阵 B 的维度为 (4, 2)。

--- 场景设置 (Scenario Setup) ---
模拟GPU数量: 2
输入激活值维度 (seq_len, input_dim): (2, 2)
第一个线性层权重维度 (input_dim, hidden_dim): (2, 4)
第二个线性层权重维度 (hidden_dim, output_dim): (4, 2)
----------------------------------------

二、 基准计算 (模拟单 GPU)

在进行并行计算前，我们先在一个设备上完整地计算一次，作为后续验证的“正确答案”。

2.1 第一个线性层计算

intermediate_activations_baseline = input_activations @ weights_A

@ 符号是 Python 中用于 矩阵乘法 的专用运算符。在 NumPy 库中，A @ B 就等同于 np.matmul(A, B)，专门用来计算两个矩阵的乘积。

我们计算输入激活值 input_activations 与第一个权重矩阵 weights_A 的乘积，得到中间激活值。

输出结果:

--- 1. 基准计算 (在单个设备上) ---计算 intermediate_activations = input_activations @ weights_A
输入激活值 input_activations ((2, 2)):
[[7 4][8 5]]权重 weights_A ((2, 4)):
[[7 3 7 8][5 4 8 8]]--> 中间激活值 intermediate_activations_baseline ((2, 4)):
[[ 69  37  81  88][ 81  44  96 104]]

2.2 第二个线性层计算

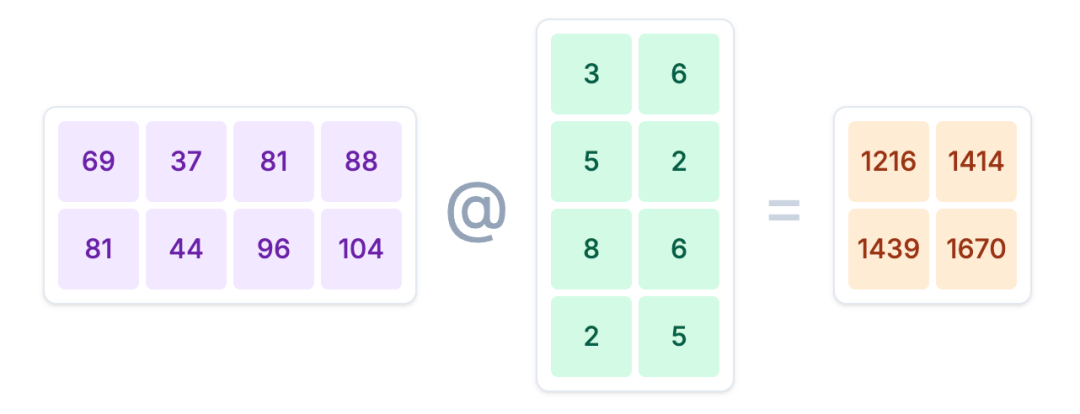
output_baseline = intermediate_activations_baseline @ weights_B

接着，用上一步得到的中间激活值 intermediate_activations_baseline 与第二个权重矩阵 weights_B 相乘，得到最终的输出结果。

输出结果:

计算 output = intermediate_activations_baseline @ weights_B
输入中间激活值 intermediate_activations_baseline ((2, 4)):
[[ 69  37  81  88][ 81  44  96 104]]权重 weights_B ((4, 2)):
[[3 6][5 2][8 6][2 5]]--> 最终输出 output_baseline ((2, 2)):
[[1216 1414][1439 1670]]

三、 模拟列并行 (Column Parallelism)

现在，我们模拟第一个线性层的“列并行”计算过程。

3.1 按列分割权重矩阵

split_size_A = hidden_dim // gpu_count
weights_A1 = weights_A[:, :split_size_A]
weights_A2 = weights_A[:, split_size_A:]

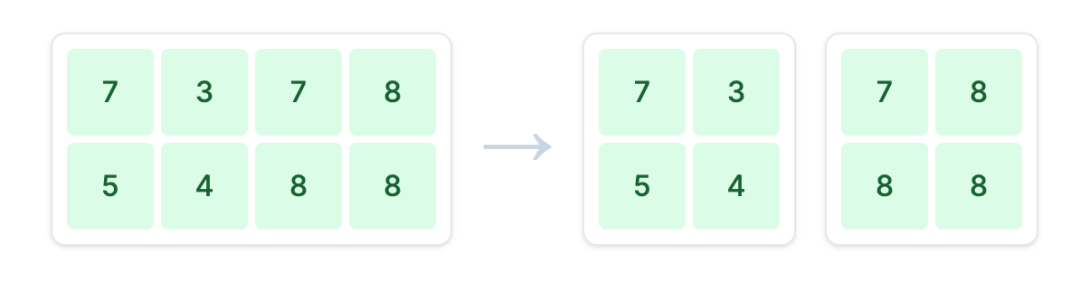
列并行的核心思想是将权重矩阵 weights_A 沿 列 的方向切分，然后将不同的切片分发给不同的 GPU。这里我们将其垂直切成 weights_A1 和 weights_A2 两部分。

输出结果:

--- 2. 模拟列并行 (第一个线性层) ---将 weights_A ((2, 4)) 按列分割成 weights_A1 ((2, 2)) 和 weights_A2 ((2, 2))

3.2 在不同 GPU 上并行计算

# GPU 0
intermediate_1 = input_activations @ weights_A1
# GPU 1
intermediate_2 = input_activations @ weights_A2

每个 GPU 使用完整的输入 input_activations 和自己分到的权重切片进行计算，得到部分的中间激活值。

输出结果:

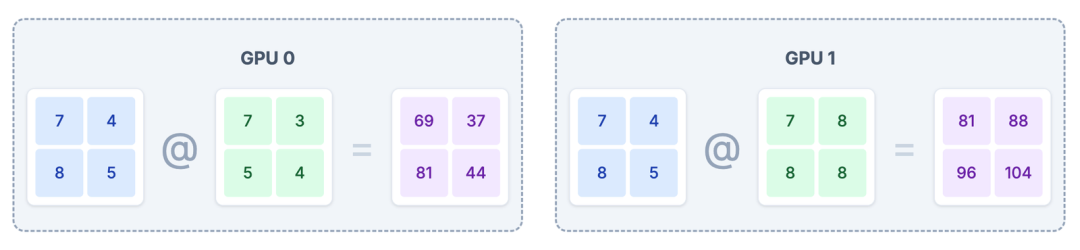
--- GPU 0 计算: intermediate_1 = input_activations @ weights_A1 ---
输入激活值 input_activations ((2, 2)):
[[7 4][8 5]]
权重切片 weights_A1 ((2, 2)):
[[7 3][5 4]]
--> 输出中间激活值切片 intermediate_1 ((2, 2)):
[[69 37][81 44]]--- GPU 1 计算: intermediate_2 = input_activations @ weights_A2 ---
输入激活值 input_activations ((2, 2)):
[[7 4][8 5]]
权重切片 weights_A2 ((2, 2)):
[[7 8][8 8]]
--> 输出中间激活值切片 intermediate_2 ((2, 2)):
[[ 81  88][ 96 104]]

3.3 聚合结果 (All-Gather)

intermediate_activations_tp = np.concatenate((intermediate_1, intermediate_2), axis=1)

在各自完成计算后，需要通过 All-Gather 操作将所有 GPU 上的计算结果 intermediate_1 和 intermediate_2 沿列（axis=1）拼接起来，恢复完整的中间激活值。注意：这里面的All-Gather 只是为了方便跟前面的单 GPU 计算结果进行对照，在实际计算过程中不需要这一步。

输出结果:

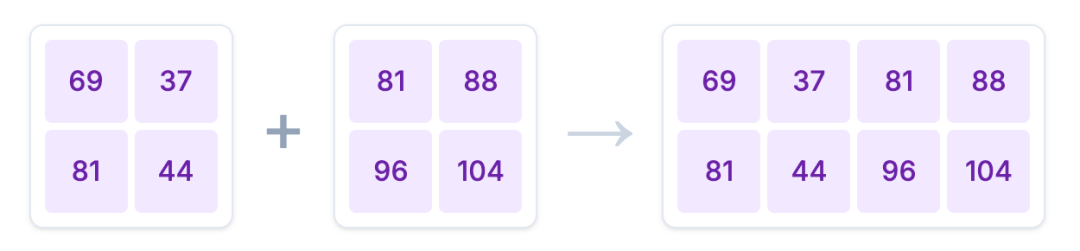
--- All-Gather 聚合 ---
拼接 intermediate_1 和 intermediate_2 得到 intermediate_activations_tp ((2, 4)):
[[ 69  37  81  88][ 81  44  96 104]]

3.4 验证结果

is_close_intermediate = np.allclose(intermediate_activations_baseline, intermediate_activations_tp)
assert is_close_intermediate, "列并行计算结果与基准不符!"

最后，我们验证并行计算的结果与基准结果是否一致。

输出结果:

列并行结果验证: ✅ 成功

四、 模拟行并行 (Row Parallelism)

接下来，我们模拟第二个线性层的“行并行”计算过程。行并行的输入是上一步列并行得到的、已经被切分在不同 GPU 上的中间激活值。

4.1 按行分割权重矩阵

split_size_B = hidden_dim // gpu_count
weights_B1 = weights_B[:split_size_B, :]
weights_B2 = weights_B[split_size_B:, :]

与列并行相反，行并行将权重矩阵 weights_B 沿 行 的方向切分，分发给不同的 GPU。

输出结果:

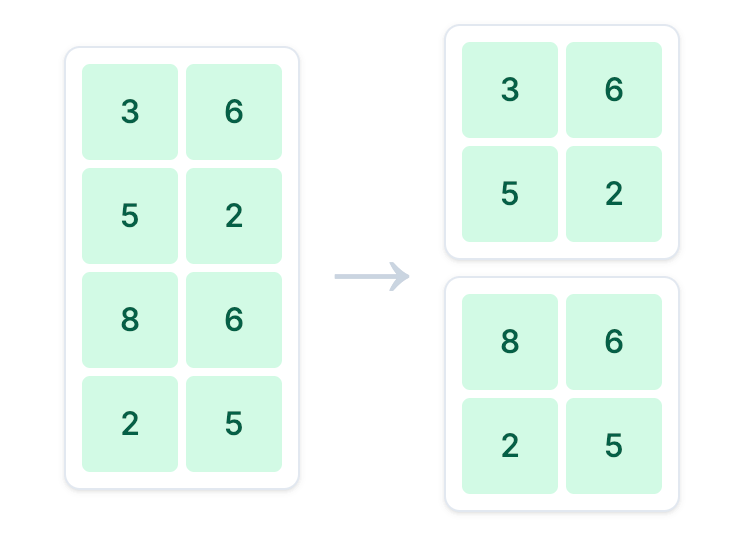
--- 3. 模拟行并行 (第二个线性层) ---将 weights_B ((4, 2)) 按行分割成 weights_B1 ((2, 2)) 和 weights_B2 ((2, 2))

4.2 在不同 GPU 上并行计算

# GPU 0
output_part_1 = intermediate_1 @ weights_B1
# GPU 1
output_part_2 = intermediate_2 @ weights_B2

每个 GPU 使用自己拥有的 部分 中间激活值（intermediate_1 或 intermediate_2）和 部分 权重（weights_B1 或 weights_B2）进行计算，得到最终输出的一个部分。

输出结果:

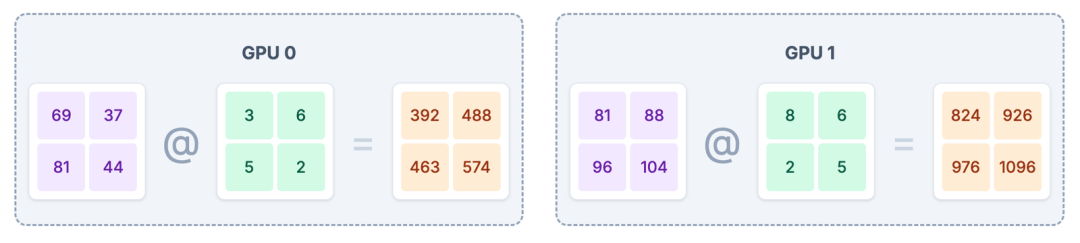
--- GPU 0 计算: output_part_1 = intermediate_1 @ weights_B1 ---
输入中间激活值切片 intermediate_1 ((2, 2)):
[[69 37][81 44]]
权重切片 weights_B1 ((2, 2)):
[[3 6][5 2]]
--> 输出部分结果 output_part_1 ((2, 2)):
[[392 488][463 574]]--- GPU 1 计算: output_part_2 = intermediate_2 @ weights_B2 ---
输入中间激活值切片 intermediate_2 ((2, 2)):
[[ 81  88][ 96 104]]
权重切片 weights_B2 ((2, 2)):
[[8 6][2 5]]
--> 输出部分结果 output_part_2 ((2, 2)):
[[ 824  926][ 976 1096]]

4.3 聚合结果 (All-Reduce)

output_tp = output_part_1 + output_part_2

行并行计算完成后，需要通过 All-Reduce 操作将所有 GPU 上的部分输出 相加，得到最终的完整输出。

输出结果:

--- All-Reduce 聚合 ---
求和 output_part_1 + output_part_2 得到最终输出 output_tp ((2, 2)):
[[1216 1414][1439 1670]]

4.4 验证结果

is_close_output = np.allclose(output_baseline, output_tp)
assert is_close_output, "行并行计算结果与基准不符!"

我们再次验证行并行计算的最终结果与基准结果是否一致。

输出结果:

行并行结果验证: ✅ 成功

通过这个过程，我们清晰地看到，通过对权重矩阵进行巧妙的切分（列并行或行并行），并将计算任务分配到不同设备上，最后通过特定的通信操作（All-Gather 或 All-Reduce）聚合结果，可以实现与单设备计算完全相同的结果，这就是张量并行的基本原理。

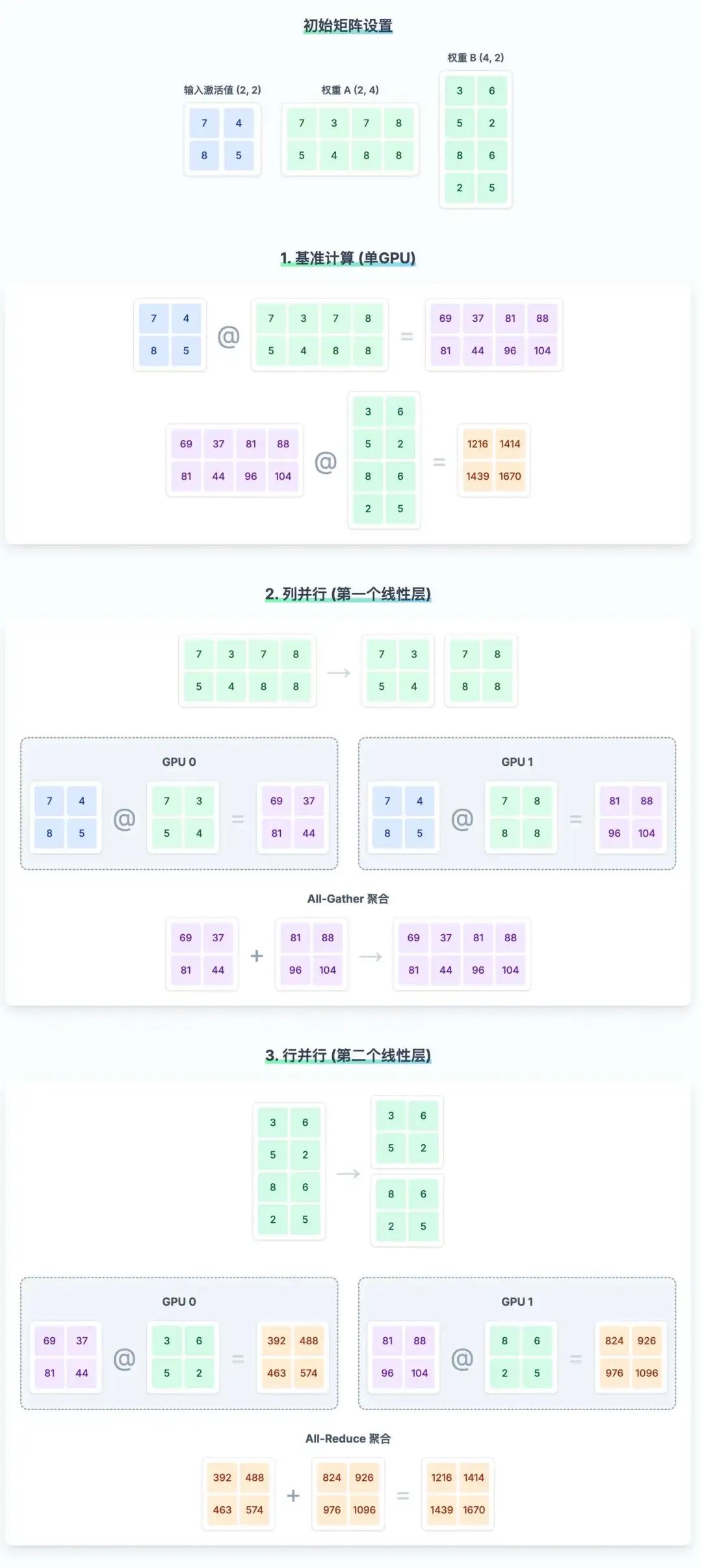
上面是整个完整过程的图示，眼尖的你可能会发现，计算过程里面是不是少了激活函数？确实，我省略了非线性激活函数（如 GeLU 或 ReLU）。

在一个完整的 Transformer MLP 模块中，其计算流程应该是：

  1. 第一个线性层（列并行）: intermediate = input @ weights_A

  2. 激活函数（逐元素操作）: activated_intermediate = GeLU(intermediate)

  3. 第二个线性层（行并行）: output = activated_intermediate @ weights_B

为什么在演示中省略了它？主要原因是为了简化并聚焦于核心概念。这个可视化的主要目的是清晰地展示张量并行如何处理矩阵乘法（线性层）这一计算瓶颈，即：

  • 如何通过列切分权重 A 来实现第一个线性层的并行（Column Parallelism）。

  • 如何通过行切分权重 B 来实现第二个线性层的并行（Row Parallelism）。

  • 以及后续的 All-Reduce 通信操作。

激活函数（如 GeLU）是一个逐元素（element-wise）的操作。在并行计算的场景下，它非常简单：每个 GPU 只需对自己本地持有的那部分中间激活值（intermediate_1 和 intermediate_2）独立应用激活函数即可，不需要任何跨 GPU 的通信。

因此，为了让演示不被枝节带偏，我们暂时省略了这一步，以便让大家能更清楚地看到矩阵分割与聚合的完整过程。

ColumnParallelLinear和RowParallelLinear源码分析

在通过 NumPy 模拟理解了张量并行的基本原理后，我们现在来深入分析 vLLM 中实现这一机制的核心 PyTorch 代码：ColumnParallelLinear 和 RowParallelLinear，以及它们的抽象基类 LinearBase。

1.LinearBase：并行线性层的基石

LinearBase 是一个抽象基类（nn.Module），它为所有并行的线性层提供了基础框架和通用属性。

class LinearBase(nn.Module):def __init__(self,input_size: int,output_size: int,tp_dim: int | None = None,):super().__init__()self.input_size = input_sizeself.output_size = output_sizeself.tp_dim = tp_dim # 张量并行的维度 (0 for column, 1 for row)self.tp_rank = dist.get_rank() # 当前 GPU 的 rankself.tp_size = dist.get_world_size() # 并行组的大小 (GPU 数量)def forward(self, x: torch.Tensor) -> torch.Tensor:raise NotImplementedError

源码解析：

  • __init__方法:

    • 它初始化了所有并行层都需要的通用参数。

    • input_size 和 output_size：定义了整个（未分割前）线性层的输入和输出维度。

    • tp_dim：这是一个关键参数，用于标识张量是在哪个维度上进行切分的。我们约定 0 代表列并行（在输出维度上切分），1 代表行并行（在输入维度上切分）。

    • tp_rank 和 tp_size：通过 torch.distributed 获取当前 GPU 在分布式环境中的排名（rank）和总数（world size），这对于加载正确的数据分片至关重要。

  • forward方法:

    • 它被定义为必须由子类实现的抽象方法，因为列并行和行并行的前向传播逻辑是不同的。

2.ColumnParallelLinear：实现列并行

这个类继承自 LinearBase，实现了列并行功能。它对应我们 NumPy 示例中的第一个线性层计算。

class ColumnParallelLinear(LinearBase):def __init__(self,input_size: int,output_size: int,bias: bool = False,):super().__init__(input_size, output_size, 0)self.input_size_per_partition = input_sizeself.output_size_per_partition = divide(output_size, self.tp_size)self.weight = nn.Parameter(torch.empty(self.output_size_per_partition, self.input_size))self.weight.weight_loader = self.weight_loaderif bias:self.bias = nn.Parameter(torch.empty(self.output_size_per_partition))self.bias.weight_loader = self.weight_loaderelse:self.register_parameter("bias", None)def weight_loader(self, param: nn.Parameter, loaded_weight: torch.Tensor):param_data = param.datashard_size = param_data.size(self.tp_dim) # self.tp_dim = 0start_idx = self.tp_rank * shard_sizeloaded_weight = loaded_weight.narrow(self.tp_dim, start_idx, shard_size)param_data.copy_(loaded_weight)def forward(self, x: torch.Tensor) -> torch.Tensor:# 输入 x 是完整的，未经切分return F.linear(x, self.weight, self.bias)

源码解析：

  • __init__方法:

    • super().__init__(..., 0)：明确设置 tp_dim=0，表示这是一个列并行层。

    • output_size_per_partition：将总的 output_size 除以 GPU 数量 tp_size。这正是列并行的核心：将权重矩阵 W 按列（输出维度）切分。

    • self.weight：权重参数 weight 的形状是 (output_size_per_partition, input_size)，即每个 GPU 只持有权重矩阵的一部分列。

  • weight_loader方法:

    • 这个辅助函数负责将一个完整的权重张量（loaded_weight）正确地切分并加载到当前 GPU 的 param 中。

    • 它使用 torch.Tensor.narrow 方法，根据当前 GPU 的 tp_rank，从完整权重的第 0 维（列）中，提取出属于自己的那一块。

  • forward方法:

    • 输入 x 是完整的、未切分的张量。

    • 它执行标准的线性运算 F.linear(x, self.weight, self.bias)。

    • 由于 self.weight 是按列切分的，所以输出张量也是按列（特征维度）切分的。这个切分后的输出可以直接作为后续行并行层的输入。这里不需要通信操作（如 All-Gather），因为下一个层（RowParallelLinear）被设计为直接处理这种切分后的输入。

3.RowParallelLinear：实现行并行

这个类同样继承自 LinearBase，它接收 ColumnParallelLinear 的输出，并执行行并行计算。它对应我们 NumPy 示例中的第二个线性层计算。

class RowParallelLinear(LinearBase):def __init__(self,input_size: int,output_size: int,bias: bool = False,):super().__init__(input_size, output_size, 1)self.input_size_per_partition = divide(input_size, self.tp_size)self.output_size_per_partition = output_sizeself.weight = nn.Parameter(torch.empty(self.output_size, self.input_size_per_partition))self.weight.weight_loader = self.weight_loaderif bias:self.bias = nn.Parameter(torch.empty(self.output_size))self.bias.weight_loader = self.weight_loaderelse:self.register_parameter("bias", None)def weight_loader(self, param: nn.Parameter, loaded_weight: torch.Tensor):param_data = param.datashard_size = param_data.size(self.tp_dim) # self.tp_dim = 1start_idx = self.tp_rank * shard_sizeloaded_weight = loaded_weight.narrow(self.tp_dim, start_idx, shard_size)param_data.copy_(loaded_weight)def forward(self, x: torch.Tensor) -> torch.Tensor:# 输入 x 是按特征维度切分过的y = F.linear(x, self.weight, self.bias if self.tp_rank == 0elseNone)if self.tp_size > 1:dist.all_reduce(y) # 对所有 GPU 的结果求和return y

源码解析：

  • __init__方法:

    • super().__init__(..., 1)：明确设置 tp_dim=1，表示这是一个行并行层。

    • input_size_per_partition：将总的 input_size 除以 GPU 数量。这是因为它的输入 x（来自前一个列并行层）的特征维度是切分过的。

    • self.weight：权重参数 weight 的形状是 (output_size, input_size_per_partition)。这正是行并行的核心：将权重矩阵 W 按行（输入维度）切分。

  • weight_loader方法:

    • 与 ColumnParallelLinear 类似，但它是在第 1 维（行）上对权重进行切分加载。

  • forward方法:

    • 输入 x 是一个在特征维度上被切分了的张量。

    • 每个 GPU 使用自己的部分输入 x 和部分权重 self.weight 计算出一个部分的输出 y。

    • dist.all_reduce(y)：这是行并行的关键步骤。该操作会将所有 GPU 计算出的部分结果 y逐元素相加，并将最终的完整结果同步到所有 GPU 上。这完美对应了 NumPy 示例中的 output_part_1 + output_part_2。

    • Bias 处理：注意 bias 只在 tp_rank == 0 的 GPU 上添加，这是因为 all_reduce 会将所有 GPU 的结果相加，如果不做处理，bias 会被加 tp_size 次。通过只在一个 GPU 上添加，可以保证最终结果的正确性。

通过这三个类的精妙设计与协作，nano-vllm 高效地实现了张量并行，将大模型的计算压力分散到多个 GPU 上，同时保证了计算结果的准确性。

QKVParallelLinear源码分析

在 Transformer 模型中，注意力（Attention）机制需要分别计算查询（Query）、键（Key）和值（Value）三个投影。一种常见的优化是使用一个单独的、更宽的线性层一次性计算出 Q, K, V，然后再将结果切分开。QKVParallelLinear 就是这个优化方法的实现，它继承自 ColumnParallelLinear，专门用于高效地并行计算 Q, K, V 投影。

class QKVParallelLinear(ColumnParallelLinear):def __init__(self,hidden_size: int,head_size: int,total_num_heads: int,total_num_kv_heads: int | None = None,bias: bool = False,):self.head_size = head_sizeself.total_num_heads = total_num_heads# 支持分组查询注意力 (GQA)，如果 K/V 头数未指定，则默认为 Q 的头数self.total_num_kv_heads = total_num_kv_heads or total_num_headstp_size = dist.get_world_size()# 计算每个 GPU 分到的头数self.num_heads = divide(self.total_num_heads, tp_size)self.num_kv_heads = divide(self.total_num_kv_heads, tp_size)input_size = hidden_size# 计算融合后的总输出维度output_size = (self.total_num_heads + 2 * self.total_num_kv_heads) * self.head_size# 调用父类 ColumnParallelLinear 的初始化方法super().__init__(input_size, output_size, bias)def weight_loader(self, param: nn.Parameter, loaded_weight: torch.Tensor, loaded_shard_id: str):param_data = param.dataassert loaded_shard_id in ["q", "k", "v"]# 根据加载的是 Q, K, 还是 V，计算在本地权重中的偏移量if loaded_shard_id == "q":shard_size = self.num_heads * self.head_sizeshard_offset = 0elif loaded_shard_id == "k":shard_size = self.num_kv_heads * self.head_sizeshard_offset = self.num_heads * self.head_sizeelse: # loaded_shard_id == "v"shard_size = self.num_kv_heads * self.head_sizeshard_offset = self.num_heads * self.head_size + self.num_kv_heads * self.head_size# 定位到本地参数中要填充的区域param_data = param_data.narrow(self.tp_dim, shard_offset, shard_size)# 将完整的 Q/K/V 权重按列切分，获取当前 rank 对应的分片loaded_weight = loaded_weight.chunk(self.tp_size, self.tp_dim)[self.tp_rank]# 将权重分片拷贝到指定位置param_data.copy_(loaded_weight)

源码解析：

  • __init__方法:

    • input_size 就是模型的 hidden_size。

    • output_size 是 Q, K, V 三者维度之和。对于支持 GQA 的模型，总输出维度为 (Q头数 + K头数 + V头数) * 每个头的维度。

    • 目的：初始化一个能够同时处理 Q, K, V 计算的列并行层。

    • 参数：除了标准的 hidden_size 和 bias，它还接收 head_size（每个头的维度）、total_num_heads（Q 的总头数）和 total_num_kv_heads（K 和 V 的总头数）。支持 total_num_kv_heads 是为了兼容分组查询注意力（Grouped-Query Attention, GQA），其中 K 和 V 的头数可以少于 Q。

    • 维度计算：

    • 继承与初始化：它计算出总的 output_size 后，直接调用父类 ColumnParallelLinear 的 __init__ 方法。这意味着 QKVParallelLinear 本质上就是一个权重矩阵被按列（输出维度）切分到不同 GPU 上的 ColumnParallelLinear 层。

  • weight_loader方法:

    • 目的：这是 QKVParallelLinear 的核心所在。它重写了父类的 weight_loader，以一种更复杂的方式加载权重。因为 Q, K, V 的权重通常是分开存储的，需要被正确地加载到这个融合后的大权重矩阵的相应位置。

    • loaded_shard_id：这个参数至关重要，它告诉加载器当前正在加载的是 "q", "k", 还是 "v" 的权重。

    • 加载逻辑：

    1. 计算偏移量 (shard_offset**)**：根据 loaded_shard_id，代码计算出当前权重（Q, K 或 V）应该被放置在每个 GPU 本地持有的权重分片中的哪个位置。例如，Q 放在最前面（偏移量为0），K 跟在 Q 后面，V 跟在 K 后面。

    2. 定位本地参数区域：使用 param_data.narrow() 从本地的融合大权重中精确地切出将要填充 Q, K, 或 V 的小区域。

    3. 切分加载权重：使用 loaded_weight.chunk() 将完整的 Q, K, 或 V 权重矩阵沿着并行维度（tp_dim=0，即列）切分成 tp_size 块，并取出当前 GPU (tp_rank) 应该持有的那一块。

    4. 拷贝数据：最后，将切分好的权重数据 copy_ 到上一步定位好的本地参数区域。

  • forward方法：

    • QKVParallelLinear没有重写 forward 方法，它直接复用了父类 ColumnParallelLinear.forward 的实现。

    • 这意味着在前向传播时，它将完整的输入 x 与其本地持有的、融合了 Q, K, V 的部分权重进行一次标准的线性运算。

    • 其输出是一个融合了 Q, K, V 结果的张量，并且这个张量是按列（特征维度）切分的。后续的逻辑需要将这个融合的输出张量再次切分，以分别得到并行的 Q, K, V 张量，用于后续的注意力计算。

从代码上面看比较抽象，下面我举个例子解释一下 QKV 在weight_loader 中是怎么从三个矩阵合并成一个矩阵的。

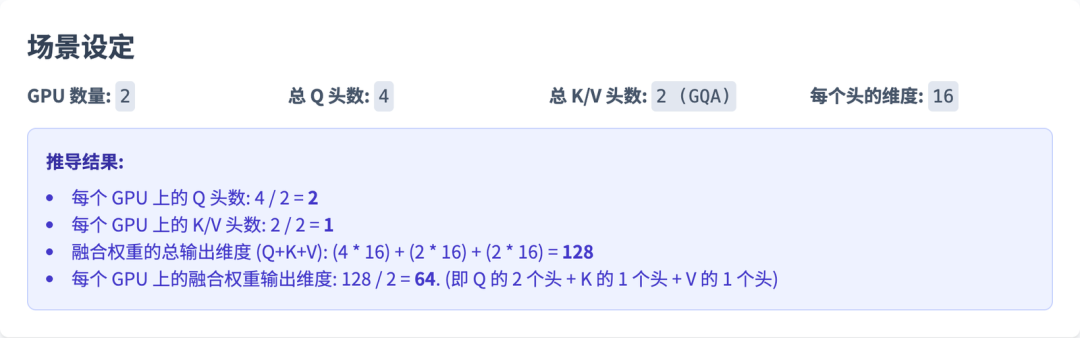
以 GPU0 为例，W_q 是 (4, 2) 的矩阵，切一半 W_q0 放到 Wfused 中。

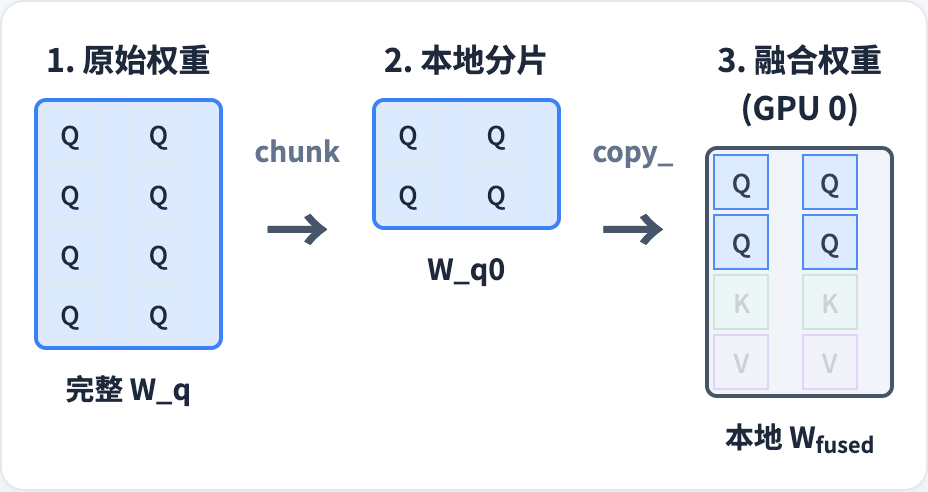
同理，K 和 V 矩阵也是这样进行切分，然后合并到一个矩阵里面。

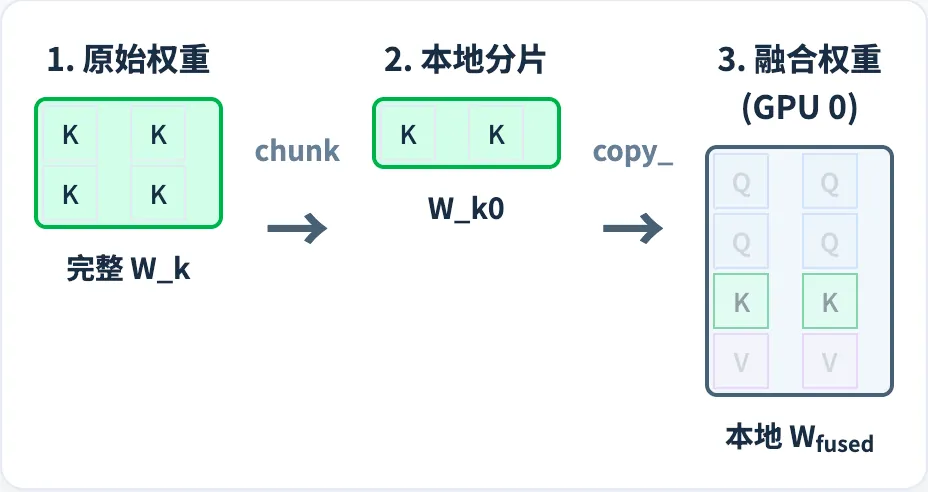
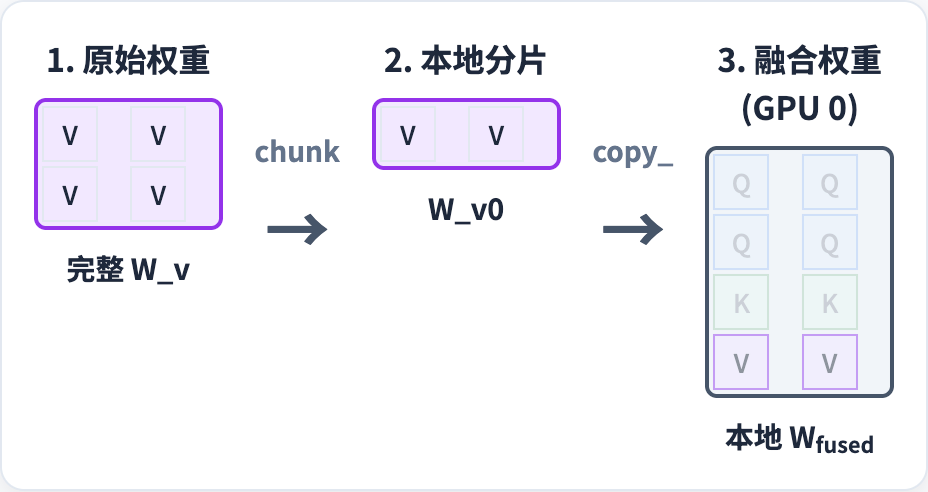
列并行切分的反直觉问题

如果你仔细看会发现，怎么 QKV 的列并行切分在图里面是按照行进行切分的？跟前面的 Numpy 例子对不上呀？好问题，这里面就涉及数学·实现跟 Pytorch 实现的差别了。

在标准的线性代数和 NumPy 中，我们这样表示矩阵乘法：

Y = X @ W
X 的形状是 (..., C_in)
W 的形状是 (C_in, C_out)
Y 的形状是 (..., C_out)

“列并行”的目标是切分输出 Y 的列，也就是它的 C_out 维度。为了实现这一点，我们必须对权重 W 的 C_out 维度进行切分。

由于 W 的形状是 (C_in, C_out)，C_out 是它的第 1 维。对第 1 维进行切分，就是垂直方向的“按列切”。

而在 PyTorch 的 nn.Linear(C_in, C_out) 层为了计算效率，存储其权重参数的方式是转置的。

  • 实际存储的 weight.shape = (C_out, C_in)

  • 层定义: layer = nn.Linear(C_in, C_out)

  • 权重形状: layer.weight.shape 是 (C_out, C_in)

  • 前向传播: 逻辑上等价于 X @ layer.weight.T

“列并行”的目标不变：我们仍然要切分输出 Y 的列，也就是 C_out 维度。

但是，在 PyTorch 存储的这个权重张量里，C_out 维度现在是它的第 0 维。对第 0 维进行切分，就是水平方向的“按行切”。

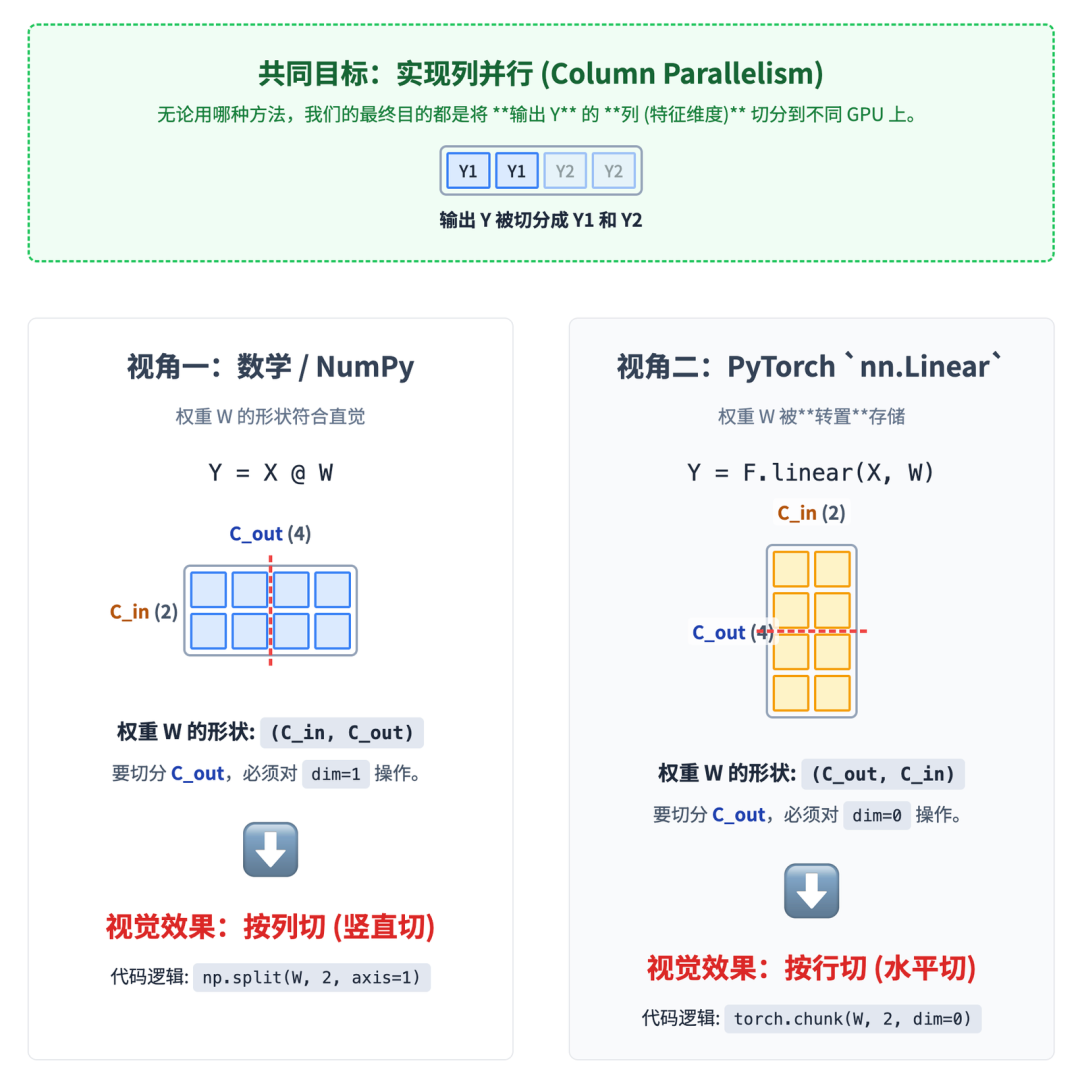
继续深挖：PyTorch 为什么要转置存储矩阵

PyTorch nn.Linear 层以转置的方式存储权重（即形状为 (C_out, C_in))，主要是为了最大化计算性能，这与现代计算机硬件（尤其是 GPU）的内存访问模式密切相关。

核心原因可以归结为一点：内存访问的连续性。

让我们来详细解释一下：

硬件工作原理：

  • 无论是 CPU 还是 GPU，从主内存中读取数据都不是一个一个字节地读取，而是一次性读取一个连续的内存块（Chunk）。

  • 对于 GPU 来说，这种特性更为重要。当多个计算核心（线程）需要访问内存时，如果它们访问的地址是连续的，GPU 就可以将这些访问合并成一次或几次大的读取操作。这个过程就叫做“合并内存访问” (Memory Coalescing)。

  • 合并访问的效率极高，而非连续的、跳跃式的（Strided）内存访问效率则会低很多，因为需要进行多次独立的内存读取操作。

矩阵乘法中的内存访问：

  • 我们来看计算 Y = X @ W.T 的过程（这是 F.linear 的逻辑）。输入 X 的形状是 (batch_size, C_in)，权重 W 的形状是 (C_out, C_in)。

  • 为了计算输出 Y 的第一个元素 Y[0, 0]，我们需要用 X 的第一行和 W 的第一行做点积。

  • 为了计算 Y[0, 1]，我们需要用 X 的第一行和 W 的第二行做点积。

  • ...以此类推。

转置存储的优势：

  • 当权重 W 以 (C_out, C_in) 的形状存储时，它的每一行在内存中是连续存放的。

  • 在计算过程中，当我们要用 X 的某一行去和 W 的所有行分别做点积时，GPU 可以非常高效地、连续地读取 W 的数据。W 的第一行读完，紧接着就是第二行的数据，内存访问是连续的、合并的。

不转置存储的劣势：

  • 如果权重 W 以 (C_in, C_out) 的形状存储，那么它的每一列在内存中是连续的，而每一行的数据则是跳跃式存储的。

  • 在计算 Y = X @ W 时，为了计算 Y 的一行，你需要用 X 的一行去和 W 的每一列做点积。

  • 这意味着你需要跳跃式地访问 W 的内存（访问第一列的第一个元素，然后跳到第二列的第一个元素，再跳到第三列...），这无法形成合并访问，效率会大大降低。

总之，PyTorch 将 nn.Linear 的权重设计为 (C_out, C_in) 的转置形式，是为了让矩阵乘法在底层硬件上执行时，对权重矩阵的内存访问模式是最高效的连续读取模式**。这是深度学习框架在设计时，为了压榨出极致的硬件性能而做出的一个关键优化。

理解张量并行的input_size和output_size

我们在理解张量并行的时候需要时刻记住：

  • 列并行: output_size 被分割，每个GPU处理部分输出维度

  • 行并行: input_size 被分割，每个GPU处理部分输入维度

那么在大模型中，input_size 和 output_size 到底代表了什么？其实这两个变量在不同组件中有不同的含义。

词嵌入层 (Word Embedding)

  • input_size: 词汇表大小 (vocab_size)

  • output_size: 隐藏层维度 (hidden_size)

  • 例如：32000 → 4096

注意力机制中的线性层

  • QKV投影:

    • input_size: hidden_size

    • output_size: num_heads × head_dim × 3 (Q、K、V三个矩阵，标准 MHA)

  • 输出投影:

    • input_size: num_heads × head_dim

    • output_size: hidden_size

前馈网络 (FFN)

  • 第一层 (上投影):

    • input_size: hidden_size

    • output_size: intermediate_size (通常是hidden_size的3-4倍)

  • 第二层 (下投影):

    • input_size: intermediate_size

    • output_size: hidden_size

输出层 (Language Modeling Head)

  • input_size: hidden_size

  • output_size: vocab_size

具体例子

以 Qwen3 0.6B 为例：

hidden_size = 1024
intermediate_size = 3072
num_heads = 16
num_kv_heads = 8
head_dim = 128
vocab_size = 151936线性层尺寸：
- 词嵌入: 151936 → 1024
- QKV投影: 1024 → 4096 (1024 → (16+8+8)×128)(GQA)
- 注意力输出: 2048 → 1024
- FFN第一层: 1024 → 3072
- FFN第二层: 3072 → 1024
- 输出层: 1024 → 151936

张量并行是对矩阵计算进行加速的技术，它是功能无关的，在理解它的时候要结合所在的组件的input_size和output_size 含义去分析，不然可能会被绕晕了。

总结

在这篇文章中，我们详细探讨了如何在大模型推理引擎中实现张量并行。张量并行是将大模型的计算任务分解到多个GPU上，以解决单个GPU显存不足的问题，并提升计算速度。通过Qwen3Attention模块中的QKVParallelLinear和RowParallelLinear两个核心组件，展示了张量并行的实现。

  1. 列并行（Column Parallelism）：通过将权重矩阵按列切分，每个GPU处理部分输出维度。QKVParallelLinear通过一次性计算Q, K, V来优化注意力机制，并将其结果切分到各个GPU上。

  2. 行并行（Row Parallelism）：通过将权重矩阵按行切分，每个GPU处理部分输入维度。RowParallelLinear接收列并行的输出，并在各个GPU上分别计算，最后通过All-Reduce操作聚合结果。

我们还解释了张量并行的数学原理和PyTorch实现中的内存优化策略，特别是如何通过转置存储权重来提高计算效率。

在理解了张量并行的基础模块（QKVParallelLinear和RowParallelLinear）之后，我们下一篇文章将聚焦于Qwen3Attention模块的核心——Attention机制本身。我们将探讨如何运用这些并行化后的Q, K, V张量来执行注意力计算，并深入分析RotaryEmbedding（旋转位置编码）如何融入其中。最终，看清所有组件是如何协同工作，完成一个完整且高效的并行化Attention操作。

关于我们

看到这里，相信你对本文核心主题已经有了更深入的理解。但 AI 和大模型领域更新迭代极快，单篇文章的内容很难覆盖所有细节，只能算是入门铺垫。

我平时会在【小灰熊大模型】这个公・Z・号里，系统整理 AI 大模型相关的实用资料，比如最新模型技术白皮书、实战调参手册、行业落地案例合集，还会每周更新 AI 前沿动态速递。

里面沉淀的干货具体包括：

  • 大模型入门学习路线图，帮新手少走弯路
  • 大模型方向必读书籍 PDF 版，方便随时查阅
  • 大模型面试题库，覆盖常见考点和高频问题
  • 大模型项目源码，可直接参考实操
  • 超详细海量大模型 LLM 实战项目，从 0 到 1 带练
  • Langchain/RAG/Agent 学习教程，聚焦热门技术方向
  • LLM 大模型系统 0 到 1 入门学习教程，适合零基础
  • 吴恩达最新大模型视频 + 课件，同步前沿课程内容

一直以来，我都在专注分享 AI 与大模型领域的干货 —— 从基础原理拆解到进阶实战教程，从开源工具测评到商业落地思考，每一篇内容都尽量打磨得细致实用，希望能帮大家快速跟上技术浪潮。

如果需要上述资料，关注后在GZH后台回复关键词【大模型福利】就能获取，后续也会持续更新更多针对性资源，一起在 AI 领域慢慢深耕成长～

http://www.dtcms.com/a/512530.html

相关文章：

  • 设计系统掉电保持参数参考
  • 机器学习：基于大数据的基金数据分析可视化系统 股票数据 金融数据 股价 Django框架 大数据技术（源码） ✅
  • 网站留言板样式洛阳青峰网络公司做网站
  • 基因数据库网站开发价格导航门户网站怎么做
  • Java Web登录系统实现（不使用开发工具）
  • 安徽省建设安全质量协会网站百度新闻官网
  • 数据结构——最短路径算法
  • SBC在企业中的应用场景
  • ai痕迹记录
  • 中建八局第一建设公司网站网站建设丨找王科杰专业
  • 网站建设的目标是什么制作简单门户网站步骤
  • C++11----新引入的默认成员函数
  • 广州商城型网站建设佛山网站建设有哪些
  • 寻找建设网站客户wordpress 是php
  • 理解 Linux 进程间通信（IPC）
  • JaveWeb后端-Web基础-SpringBoot Web、HTTP协议
  • Spring 自动注入是怎么实现的？从 @Component 到 @Autowired 的完整流程
  • 基于springboot的基于智能推荐的卫生健康系统开发与设计
  • 技术面：Spring（循环依赖，spring与springboot的区别）
  • 网站建设相关法律python破解wordpress
  • 高并发系统网络优化：TCP 参数调优、HTTP 协议优化（HTTP_2、HTTPS）
  • PostgreSQL跨数据库授权查询
  • 构建自定义命令行工具 - 打造专属指令体
  • 今日反弹有玄机：外围利好是助力!
  • 门户网站定制青岛网站建设公司招聘
  • 腾讯云做网站怎么样长沙装修公司口碑比较好的
  • 做翻译 网站php网站建设找哪家好
  • 网站建设中栏目是什么南京做代账会计在哪个网站上找
  • 2025年HR 数字化转型：从工具应用到组织能力重构的深度变革
  • 做网站需要看的书公司网站建设工作内容