MS-YOLOv11:一种用于遥感图像中小目标检测的小波增强多尺度网络
摘要
论文链接:https://www.mdpi.com/1424-8220/25/19/6008
在遥感图像中,小于 32×3232 \times 3232×32 像素的目标面临着三个现有检测器未能充分解决的持久性挑战:(1) 其微弱信号极易被背景杂波淹没,导致高漏检率;(2) 有效像素稀缺,难以提供足够的几何或纹理线索,阻碍了判别性特征的提取;(3) 连续的下采样操作不可逆地丢弃了高频细节,而多尺度金字塔结构仍然无法对此进行有效补偿。为应对这些问题,我们提出了 MS-YOLOv11,这是一种增强型 YOLOv11 变体,集成了“频域细节保留、轻量级感受野扩展和自适应跨尺度融合”。具体而言,首先使用二维 Haar 小波将图像分解为多个频率子带,以显式地分离并保留高频边缘和纹理,同时抑制噪声。然后,每个子带由小核深可分离卷积独立处理,以在不过度平滑的情况下扩大感受野。最后,混合结构块(MSB)采用 MSPLCK 模块执行密集采样的多尺度空洞卷积,以获取微小目标的丰富上下文信息,随后通过 EPA 模块利用残差连接自适应地融合和重加权特征,以抑制背景干扰。在 DOTA 和 DIOR 数据集上的大量实验表明,MS-YOLOv11 在 mAP@50、mAP@95、参数效率和推理速度方面均优于基线模型,验证了其在小目标检测方面的针对性有效性。
关键词:多尺度特征;小波变换;遥感图像;YOLOv11;小目标检测
1. 引言
随着遥感技术的飞速发展,其在环境监测 [1]、城市规划 [2] 和灾害评估 [3] 等领域的应用日益广泛。近年来,深度学习技术的应用显著增强了卷积神经网络的特征提取能力 [4]。目前,主流的目标检测算法分为两阶段和单阶段检测方法 [5]。其中,YOLO 系列 [6] 单阶段检测器在提高识别准确率方面展现出巨大潜力,并在各种计算机视觉任务中表现出强大的实用性和广阔的应用前景。此外,YOLO 系列算法的实时处理能力和计算效率为在航空航天系统中的部署提供了显著优势 [7]。随着 YOLO 架构的不断迭代和优化,它能更好地适应通用目标检测任务。
然而,遥感图像中的目标通常非常小,由于高空获取,其可区分特征有限,这限制了有效的特征提取。其次,杂乱的背景加上天气变化和光照差异等环境因素加剧了前景-背景混淆,降低了检测精度。此外,纹理和形状线索的缺乏会导致视觉上相似的小目标(例如,车辆与油罐、船只与浮桥)之间产生混淆。同时,微弱的目标信号很容易被背景杂波掩盖,导致其漏检率远高于中大型目标 [8]。因此,使用 YOLO 系列算法在遥感图像中准确检测小目标 [9] 仍然是一个重大挑战。总而言之,此类场景下小目标检测的核心挑战可归纳为以下三个方面:
- 微弱的目标信号:目标在广阔的视野和强杂波中容易被遮蔽,导致高漏检率。
- 像素信息不足:几何轮廓和纹理细节极度稀缺,使得传统卷积操作难以捕捉判别性表示。
- 高频信息丢失:连续的下采样操作不可逆地消除了边缘和纹理细节,而现有的金字塔结构仍然难以补偿细粒度的结构信息。
为解决这些挑战,本文提出了 MS-YOLO(多尺度 YOLO),专为遥感场景设计。该算法基于 YOLOv11 基线,引入了三种创新策略:频域细节保留、轻量级感受野扩展和自适应跨尺度融合。具体贡献如下:
频域细节保留:在输入阶段嵌入二维 Haar 小波变换,将图像显式分解为一个低频近似分量和三个高频细节子带。此过程在抑制背景噪声的同时,突出了容易被遮蔽的细微边缘和纹理。
轻量级感受野扩展:对每个子带独立应用小核深可分离卷积。这种方法在不引入冗余参数的情况下指数级扩展感受野,在保留全局上下文的同时避免了对小目标的过度平滑。
自适应跨尺度融合:设计了一个混合结构块(MSB),其中包括:
- 一个 MSPLCK 模块,采用并行空洞卷积 (7×7→13×13→19×197\times7 \to 13\times13 \to 19\times197×7→13×13→19×19) 进行密集采样,以捕获极小目标的多尺度上下文信息;
- 一个 EPA 模块,利用带有残差连接的双通道-空间注意力机制自适应地加权特征,动态抑制背景干扰并增强目标特征。
2. 相关工作
2.1. 目标检测方法
目标检测领域的研究呈现出从传统方法到深度学习技术的明显演变趋势。早期的传统方法主要依赖于手工设计的特征提取器和分类器的组合。基于滑动窗口机制的模板匹配方法,如 Viola-Jones 检测器(2001)[10] 和 HOG+SVM(2005)[11],通过结合 Haar 特征或方向梯度直方图来实现目标定位,但存在计算冗余高、实时性能差的问题。
随着深度学习的兴起,目标检测技术发生了根本性变革。基于卷积神经网络(CNNs)的端到端学习范式显著提高了检测精度和效率。现代深度学习方法主要遵循三条技术路径:两阶段检测器(如 R-CNN 系列(例如 Fast R-CNN, Faster R-CNN)[14])先生成区域建议,再进行分类和回归;以及后续的发展,如 FPN(通过特征金字塔网络增强多尺度特征融合)[15-17] 和 Mask R-CNN[18](扩展到实例分割任务)。这些方法在需要严格精度的场景下能达到高检测精度,但计算复杂度较高。单阶段方法(如 YOLO 系列和 SSD [19])直接在特征图上预测目标类别和位置,以牺牲部分精度换取速度优势,更适合实时应用。YOLO 系列从 YOLOv1 到最新的 YOLOv12 经历了多次迭代,融入了多尺度预测 [20]、CSPNet 骨干网络 [21]、Transformer 注意力机制 [22] 和神经架构搜索(NAS)[23] 等技术,不断平衡精度与效率。无锚框方法 [24](如 CenterNet, CornerNet, 和 DETR)放弃了预设的锚框,直接预测关键点或利用自注意力机制进行端到端检测,减少了超参数依赖,但面临训练收敛慢和计算需求高等挑战。
2.2. 小目标检测的深度学习算法
遥感图像中的小目标检测是计算机视觉领域的一项关键挑战。近年来,全球研究人员在多个方向进行了广泛研究,包括特征增强与注意力机制、多尺度特征融合、模型轻量化与高效检测,以及基于 Transformer 的新方法,极大地推动了该领域的发展。
在特征增强方面,研究人员通过引入注意力机制和特征重建技术来提高小目标的表征能力。例如,Huang 等人在 Faster R-CNN 的基础上,采用图像上采样和梯度上升方法来重建特征,同时保留细节信息。Wu 等人将空间到深度的变换与注意力机制相结合,提高了准确性和区分密集分布目标的能力。然而,这类方法通常会产生巨大的计算开销,难以满足实时检测的要求。
多尺度特征 [26] 融合是解决尺度变化问题的关键技术路径。Shan 等人将区域建议网络(RPNs)与多角度 RoI 提取 [27] 相结合,有效地利用了多层次特征。Lv 等人提出了 RT-DETR 模型,通过跨尺度融合和 IoU 感知的查询选择机制 [28] 增强了多尺度处理能力。Liu 等人进一步设计了 SO-RTDETR[29],通过引入注意力机制来平衡不同尺度目标的检测性能。尽管这些方法取得了优异的精度,但其复杂的结构和高昂的训练成本需要大量的计算资源。
此外,一系列基于 YOLO 架构的改进算法加速了小目标检测的发展。例如,LGFF-YOLO[30] 通过全局信息融合模块(GIFM)和四叶草融合模块(FLCM)来增强多尺度特征表示。FFCA-YOLO [31] 引入了特征增强模块(FEM)来扩展感受野,而 SF-YOLO [32] 则通过空间信息感知(SIP)模块优化前景-背景判别。同时,互学习(MA)[33] 等新范式通过分支协作和特征对齐进一步提高了检测性能。例如,MADet [34] 采用混合回归策略来处理多样化的对象,而 DICN [35] 则通过网络一致性 [36] 促进跨域知识迁移。
总而言之,CNNs——特别是 YOLOv11——为遥感图像中的小目标检测提供了强大的基线,提供了速度、精度和实际可部署性的良好平衡。其对局部特征提取的归纳偏置与该任务的核心挑战非常契合。虽然 Transformer [37] 在全局建模方面具有理论优势,但其计算成本对于许多实时遥感应用来说可能过高。因此,MS-YOLOv11 采用了混合方法:通过小波变换增强局部细节提取,并通过高效的注意力和多尺度机制弥补全局上下文的不足。这使得精度和速度同时得到提升,更好地满足了遥感图像中小目标检测的实际需求。
3. 提出的模型
3.1. MS-YOLO 模型概述
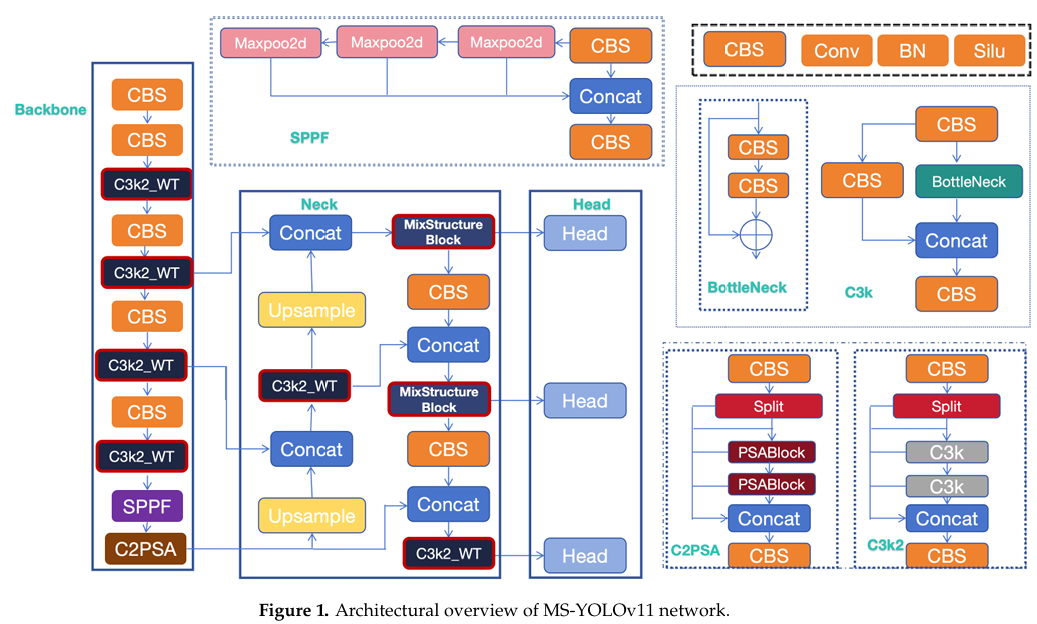
原始的 YOLOv11 架构在其骨干网络中使用了四个 C3K2 模块进行特征提取,这可能会导致特征退化。为了缓解这一限制,我们将小波变换卷积神经网络(WTCNN)模块集成到骨干网络中。这个创新模块通过小波变换进行多尺度目标分解,能够有效地捕获不同尺度的目标特征。所提出的增强不仅提高了小目标检测的准确性,还增强了在复杂场景下的多尺度目标检测性能。
在网络的颈部,混合结构块(Mix Structure Block)模块在多尺度特征融合中起着关键作用。通过将特征融合技术与残差连接相结合,该模块优化了特征表示,同时捕获了多尺度特性。这种设计显著提高了特征的鲁棒性和判别力,使其在复杂背景和可变光照条件下的检测任务中表现出色。完整的网络架构如图 1 所示。
3.2. 小波变换的算法原理
傅里叶变换将信号分解为全局正弦分量,但这种方法在分析具有强空间局部性的图像特征(如边缘和纹理模式)时存在局限性。考虑一幅图像,其左上角包含精细细节,而右下角是平滑区域:这些不同的区域需要独立的空间分析,但傅里叶变换本质上缺乏空间定位能力。这一局限性在处理非平稳图像信号时尤为明显——例如,在物体边界处的频率突变——傅里叶变换只能产生一个聚合的频谱,而无法指示高频边缘分量的空间分布 [38]。在遥感目标检测应用中,空间定位尤其关键。物体边界等基本图像特征表现为局部化的高频分量。小波变换通过在其高频子带(LH, HL, 和 HH)中直接编码空间位置信息(通过图像坐标)来解决这一根本性限制。这与傅里叶分析形成对比,后者仅能指示高频内容的全局存在,而没有空间参考。此外,小波分解自然地生成一种金字塔结构的表示(以拉普拉斯金字塔为例),便于分层、由粗到精的特征提取。这种多分辨率特性使得小波分析特别适用于目标检测和图像融合等计算机视觉任务。二维 Haar 小波变换的数学框架在算法 1 中正式给出。
本工作主要利用 Haar 小波变换(WT)的计算效率和实现优势。我们强调,我们的方法并不从根本上局限于这种特定的小波基,其他小波族也可以替代实现,尽管可能会带来更大的计算需求。

对于给定图像 XXX,单层一维 Haar WT(沿宽度或高度维度应用)通过以下方式实现:(1) 使用分析核 12[1,1]\frac{1}{\sqrt{2}}[1,1]21[1,1] 和 12[1,−1]\frac{1}{\sqrt{2}}[1,-1]21[1,−1] 进行深度卷积,然后 (2) 使用步长 2 进行标准下采样。二维扩展将这些操作结合到两个空间维度上,有效地实现为使用四组不同滤波器、步长为 2 的深度卷积:
fLL=12[1111],fLH=12[1−11−1],fHL=12[11−1−1],fHH=12[1−1−11]
\begin{array}{c c}
{{f_{L L}=\displaystyle\frac{1}{2}\left[\begin{matrix}{1}&{1}\\ {1}&{1}\end{matrix}\right],}}&{{f_{L H}=\displaystyle\frac{1}{2}\left[\begin{matrix}{1}&{-1}\\ {1}&{-1}\end{matrix}\right],}}\\
{{f_{H L}=\displaystyle\frac{1}{2}\left[\begin{matrix}{1}&{1}\\ {-1}&{-1}\end{matrix}\right],}}&{{f_{H H}=\displaystyle\frac{1}{2}\left[\begin{matrix}{1}&{-1}\\ {-1}&{1}\end{matrix}\right]}}
\end{array}
fLL=21[1111],fHL=21[1−11−1],fLH=21[11−1−1],fHH=21[1−1−11]
这里,fLLf_{LL}fLL 作为低通滤波器,而 fLH,fHL,f_{LH}, f_{HL},fLH,fHL, 和 fHHf_{HH}fHH 构成互补的高通滤波器。对每个输入通道的卷积操作产生以下结果:
[XLL,XLH,XHL,XHH]=Conv(⌈fLL,fLH,fHL,fHH⌉,X),[X_{L L},X_{L H},X_{H L},X_{H H}]=\mathrm{Conv}\big(\lceil f_{L L},f_{L H},f_{H L},f_{H H}\rceil,{\bf X}\big),[XLL,XLH,XHL,XHH]=Conv(⌈fLL,fLH,fHL,fHH⌉,X),
生成四个输出通道,每个通道的空间分辨率相对于 XXX 减半。分量 XLL,XLH,XHL,X_{LL}, X_{LH}, X_{HL},XLL,XLH,XHL, 和 XHHX_{HH}XHH 分别代表低频近似和水平、垂直及对角线的高频细节。公式 (1) 中基滤波器的正交性允许通过转置卷积进行精确重建:
X=ConvTranspose([fLL,fLH,fHL,fHH],[XLL,XLH,XHL,XHH])\mathbf{X}=\mathbf{ConvTranspose}\big(\big[f_{L L},f_{L H},f_{H L},f_{H H}\big],\big[X_{L L},X_{L H},X_{H L},X_{H H}\big]\big)X=ConvTranspose([fLL,fLH,fHL,fHH],[XLL,XLH,XHL,XHH])
级联小波分解通过对低频分量递归应用来实现:
XLL(i),XLH(i),XHL(i),XHH(i)=WT (XLL(i−1))X_{L L}^{\left(i\right)},X_{L H}^{\left(i\right)},X_{H L}^{\left(i\right)},X_{H H}^{\left(i\right)}=\mathsf{W T}\!\left(X_{L L}^{\left(i-1\right)}\right)XLL(i),XLH(i),XHL(i),XHH(i)=WT(XLL(i−1))
其中上标 (i)(i)(i) 表示分解层级。这一分层过程在降低低频分量空间分辨率的同时,逐步提高了频率分辨率。
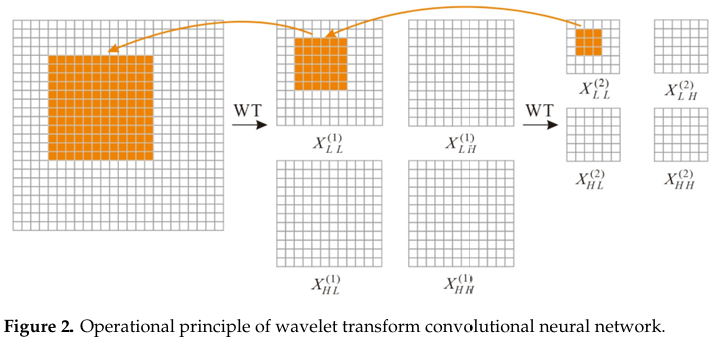
值得注意的是,小波域中的卷积操作可以扩展感受野。例如,对第二级低频分量 XLL(2)X_{LL}^{(2)}XLL(2) 应用一个 3×33\times33×3 卷积,实际上相当于在原始输入 XXX 上为低频信号处理建立了一个覆盖 12×1212 \times 1212×12 感受野的九参数核。
3.3. 小波变换卷积神经网络
随着卷积核尺寸的增加,参数呈二次方增长,这是一个重大挑战。我们的解决方案包括三个阶段:(1) 对输入的低/高频分量进行基于小波的滤波和下采样,(2) 在特定频率的特征图上进行小核深度卷积,(3) 通过逆小波变换进行输出重建。数学上,此操作表示为:
Y=IWT(Conv (W,WT (X)))Y=\operatorname{IWT}(\operatorname{Conv}\!\left(W,\operatorname{WT}\!\left(X\right)\right))Y=IWT(Conv(W,WT(X)))
其中 XXX 表示输入张量,WWW 表示 k×kk \times kk×k 深度卷积核的权重张量,其输入通道数是 XXX 的四倍。这种方法不仅隔离了特定频率的卷积,还使小核能在扩展的输入区域上操作,有效地增加了它们的感受野。图 2 提供了原理示意图。
我们将此单级操作通过级联分解进行扩展,由以下递归方程定义:
XLL(i), XLH(i), XHL(i), XHH(i)=WT (XLL(i−1))X_{L L}^{\left(i\right)},\;X_{L H}^{\left(i\right)},\;X_{H L}^{\left(i\right)},\;X_{H H}^{\left(i\right)}=\mathsf{W T}\!\left(X_{L L}^{\left(i-1\right)}\right)XLL(i),XLH(i),XHL(i),XHH(i)=WT(XLL(i−1))
YLL(i), YLH(i), YHL(i), YHH(i)=Conv(W(i), (XLL(i), XLH(i), XHL(i), XHH(i)))Y_{L L}^{(i)},\;Y_{L H}^{(i)},\;Y_{H L}^{(i)},\;Y_{H H}^{(i)}=\mathsf{C o n v}\Big(W^{(i)},\;\Big(X_{L L}^{(i)},\;X_{L H}^{(i)},\;X_{H L}^{(i)},\;X_{H H}^{(i)}\Big)\Big)YLL(i),YLH(i),YHL(i),YHH(i)=Conv(W(i),(XLL(i),XLH(i),XHL(i),XHH(i)))
这里,XLL(0)X_{LL}^{(0)}XLL(0) 作为第一分解层的输入。在每一级 iii 的输出 XH(i)X_{H}^{(i)}XH(i) 包含三个高频子带 (XLH(i), XHL(i), XHH(i)ˉ)\left(\bar{X_{L H}^{\left(i\right)},\;X_{H L}^{\left(i\right)},\;X_{H H}^{\left(i\right)}}\right)(XLH(i),XHL(i),XHH(i)ˉ)。利用 WT 和 IWT 操作的线性,多级特征聚合递归地执行:
Z(i)=IWT(YLL(i)+Z(i+1), YLH(i), YHL(i), YHH(i))Z^{(i)}=\mathrm{IWT}\Big(Y_{L L}^{(i)}+Z^{(i+1)},\;Y_{L H}^{(i)},\;Y_{H L}^{(i)},\;Y_{H H}^{(i)}\Big)Z(i)=IWT(YLL(i)+Z(i+1),YLH(i),YHL(i),YHH(i))
其中 Z(i)Z^{(i)}Z(i) 表示来自第 iii 级的聚合输出,最深层 lll 的初始条件设置为 Z(ℓ+1)=0Z^{(\ell+1)}=0Z(ℓ+1)=0。与 [39] 中对每个频率子带采用独立归一化不同,我们在卷积操作后采用可学习的通道级缩放因子,使网络能够自适应地平衡来自不同频率分量的贡献。
图 2 展示了 WTCNN 在 MobileNetV2 的第三个倒残差块中的应用,显示了使用 3×33 \times 33×3 核的两级分解。
WTCNN 的集成提供了两个关键优势:(1) 通过 lll 级分解实现感受野的指数级增长 (2ℓ⋅k)(2^{\ell}\cdot k)(2ℓ⋅k),而参数仅线性增加 (ℓ⋅4⋅c⋅k2)(\ell\cdot4\cdot c\cdot k^{2})(ℓ⋅4⋅c⋅k2);(2) 通过对输入低频进行递归 WT 分解来增强低频响应,补充了标准卷积对高频的偏向。
这些技术优势带来了实际好处,包括与大核方法相比更好的可扩展性、更强的抗干扰鲁棒性以及对形状(而非纹理)的更高敏感性。
我们进一步通过小波变换图像特征来可视化多尺度特征提取(图 3)。分解清晰地将图像内容分离到不同的频带中,产生了四个特征性的特征图。
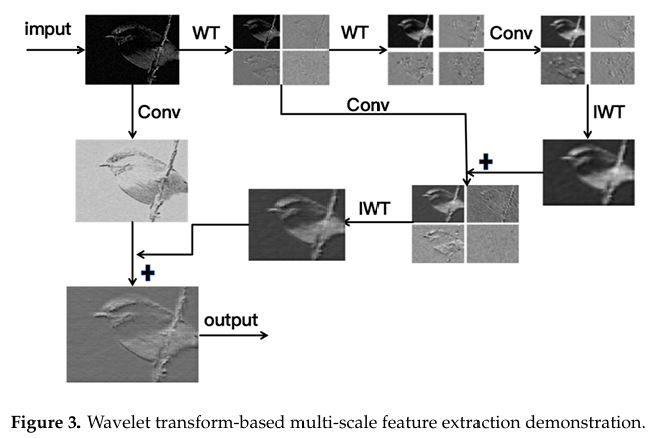
该图展示了通过二维离散小波变换对鸟类图像的分解。原始图像(“WT”)揭示了基本轮廓,而子带则突出了:(LL) 形态结构,(LH) 垂直羽毛纹理,(HL) 水平喙/爪边缘,以及 (HH) 对角线微观结构——有效地展示了从宏观形状到微观图案的分层特征提取。
3.4. 混合结构块
混合结构块集成了两个关键组件:一个多尺度并行大卷积核模块和一个增强并行注意力模块 [40],如图 4 所示。
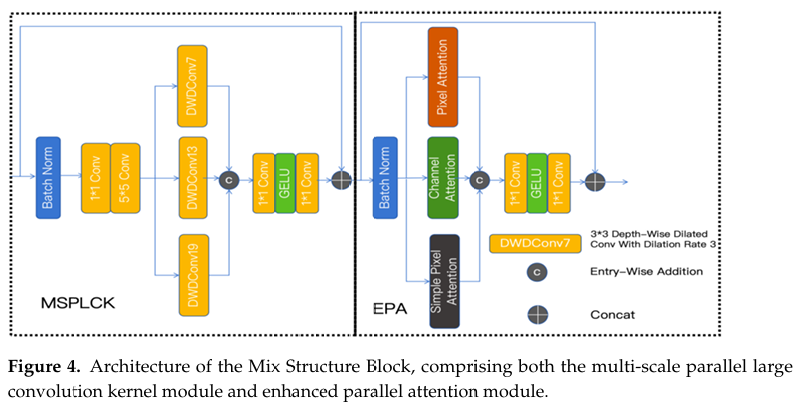
3.4.1. 多尺度并行大卷积核模块 (MSPLCK)
MSPLCK 模块协同结合了大感受野和多尺度能力。大核卷积网络不仅提供了扩展的有效感受野,而且表现出比纹理偏向更强的形状偏向。对于小目标检测任务,广泛的感受野至关重要——它使网络能够通过全局上下文信息捕获微小目标的整体结构,同时通过形状偏向精确地重建目标轮廓。
处理从原始特征图 xxx 开始,首先进行批归一化:
x^=BatchNorm(x)\hat{x}=\operatorname{BatchNorm}(x)x^=BatchNorm(x)
该模块的数据流数学表达如下:
x1=PWConv(x^),x2=Conv(x1),x3=Concat(DWDConv19(x2),DWDConv13(x2),DWDConv7(x2))
\begin{array}{r l}
&{x_{1}=\mathrm{PWConv}\big(\hat{x}\big),}\\
&{x_{2}=\mathrm{Conv}\big(x_{1}\big),}\\
&{x_{3}=\mathrm{Concat}\big(\mathrm{DWDConv}_{19}\big(x_{2}\big),}\\
&{\quad\quad\mathrm{DWDConv}_{13}\big(x_{2}\big),}\\
&{\quad\quad\mathrm{DWDConv}_{7}\big(x_{2}\big)\big)}
\end{array}
x1=PWConv(x^),x2=Conv(x1),x3=Concat(DWDConv19(x2),DWDConv13(x2),DWDConv7(x2))
其中 PWConv 表示逐点卷积,Conv 代表标准的 5×55 \times 55×5 卷积,而 DWDConvk 表示有效核大小为 1 的空洞深度可分离卷积(DWDConv19 为 7×77\times77×7 核,膨胀率为 3;DWDConv13 为 5×55\times55×5 核,膨胀率为 3;DWDConv7 为 3×33\times33×3 核,膨胀率为 3)。Concat 操作沿通道维度合并特征。
这种采用三种不同核大小的并行架构,有助于全面的多尺度特征提取。虽然较大的空洞卷积提供了广泛的感受野和显著的形状偏向——有助于利用长距离依赖定位小目标——但较小的变体则专注于精细的局部细节和纹理信息,增强了小目标的判别能力。连接操作使 x3x_3x3 的特征维度相对于 xxx 增加了三倍。
KaTeX parse error: Undefined control sequence: \upnu at position 13: \boldsymbol{\̲u̲p̲n̲u̲}=\boldsymbol{x…
随后,x3x_3x3 通过一个由两个带 GELU 激活的逐点卷积层组成的多层感知机(MLP)进行处理,将其特征维度变换回与 xxx 匹配。MLP 的输出通过残差连接与原始输入相结合,有效地整合了不同类型的特征,同时适应了小目标的特定表示需求。
3.4.2. 增强并行注意力模块
增强并行注意力(EPA)模块是一种创新架构,通过并行处理战略性地结合了互补的注意力机制。我们对小目标特征的分析表明,通道注意力机制擅长编码全局语义信息,而像素注意力操作在建模空间细粒度特征方面表现出卓越的能力。这种架构设计能够同时提取位置特定和全局共享的特征表示,使其特别适用于小目标检测任务。
EPA 框架包含三个在批归一化特征图上并行运行的注意力路径:
x^=BatchNorm(x)\hat{x}=\operatorname{BatchNorm}(x)x^=BatchNorm(x)
像素注意力分支专门用于捕获空间细粒度特征,这对于小目标的精确定位和分类至关重要。如图 5 所示。
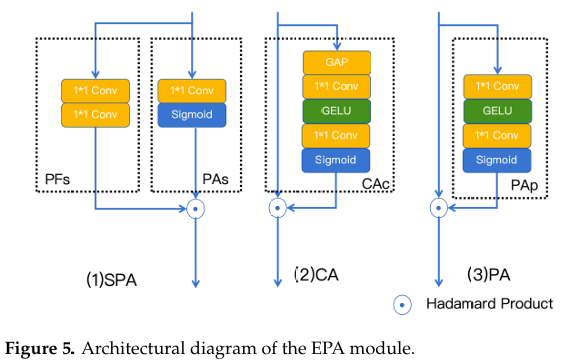
该组件包含两个主要子模块:一个特征变换分支 (PFs)(PF_s)(PFs) 和一个空间注意力门 (PAs)(PA_s)(PAs),其操作如下:
PFs=Conv3×3(PWConv(x^))PAs=σ(PWConv(x^))Fs=PFs⊙PAs
\begin{aligned}
{P F_{s}}&{{}=\operatorname{Conv}_{3\times3}(\operatorname{PWConv}(\hat{x}))}\\
{P A_{s}}&{{}=\sigma(\operatorname{PWConv}(\hat{x}))}\\
{F_{s}}&{{}=P F_{s}\odot P A_{s}}
\end{aligned}
PFsPAsFs=Conv3×3(PWConv(x^))=σ(PWConv(x^))=PFs⊙PAs
其中 PWConv 表示逐点卷积操作,σ\sigmaσ 代表 sigmoid 激活函数。扩展的像素注意力机制包含了额外的非线性变换。
通道注意力分支通过通道级特征重校准提供全局上下文建模:
CAc=σ(PWConv(GELU(PWConv(GAP(x^))))Fc=x^⊙CAc
\begin{array}{r l}
&{C A_{c}=\sigma(\mathrm{PWConv}(\mathrm{GELU}(\mathrm{PWConv}(\mathrm{GAP}(\hat{x}))))}\\
&{\quad F_{c}=\hat{x}\odot C A_{c}}
\end{array}
CAc=σ(PWConv(GELU(PWConv(GAP(x^))))Fc=x^⊙CAc
其中 GAP 表示用于空间信息聚合的全局平均池化操作。特征集成通过连接和非线性变换实现:
F=Concat (Fs,Fc,Fp)y=x+PWConv (GELU (PWConv (F)))
\begin{array}{l}
{{F=\operatorname{Concat}\!\left(F_{s},F_{c},F_{p}\right)}}\\
{{\quad y=x+\operatorname{PWConv}\!\left(\operatorname{GELU}\!\left(\operatorname{PWConv}\!\left(F\right)\right)\right)}}
\end{array}
F=Concat(Fs,Fc,Fp)y=x+PWConv(GELU(PWConv(F)))
EPA 模块因其双容量架构而在小目标检测中表现出色。对于全局语义信息,通道注意力分支生成通道级权重以增强目标的判别性特征;对于空间细节,像素注意力产生空间掩码以聚焦于小目标的局部结构。这种通过专用注意力机制对不同特征层次进行并行处理的方式,能够全面建模小目标特征,同时保持计算效率。
4. 实验
4.1. 数据集
本文使用了两个开源实验数据集:DIOR-R 数据集 [41] 和 DOTA 数据集 [42]。我们使用 DIOR-R 数据集来评估模型的性能。它包含 23,190 张遥感图像,共有 192,512 个标注目标实例,涵盖 20 个常见物体类别。所有目标实例都用一个定向边界框进行标注,以指示其在图像中的位置和方向。数据分布为 60% 用于训练,20% 用于验证,20% 用于测试。图像被调整为 640×640640 \times 640640×640 像素作为模型的输入。DOTA(航空图像中的目标检测数据集)是一个著名的用于遥感图像中定向边界框(OBB)检测的大规模数据集。它包含 2806 张图像,尺寸从 800×800800 \times 800800×800 到 4000×40004000 \times 40004000×4000 像素不等,包含 15 个类别的 188,282 个实例。该数据集有助于全面评估目标检测算法在各种航空图像上的表现,并用于验证该框架在定向目标检测任务中的准确性。定向边界框(OBB)头预测每个目标的旋转角度 θ\thetaθ,参数化范围为 [0,90∘)[0, 90^\circ)[0,90∘),并直接用其值进行回归。
4.2. 评估指标
我们使用五个指标来评估模型性能:精确率(P)、召回率(R)、平均精度均值(mAP)、F1 分数、检测速度(FPS)和小目标的 mAP(记为 mAP(small))。基于假阳性(FP)、真阳性(TP)、假阴性(FN)和真阴性(TN),P 和 R 定义如下:
R=TPTP+FNP=TPTP+FP
\begin{array}{l}
{\displaystyle{R=\frac{T P}{T P+F N}}}\\
{\displaystyle{P=\frac{T P}{T P+F P}}}
\end{array}
R=TP+FNTPP=TP+FPTP
IoU 阈值设为 0.5。随后,使用之前获得的召回率和精确率,我们绘制精确率-召回率(P-R)曲线,并将曲线下面积计算为平均精度(AP)。我们遵循 COCO 评估协议,使用几个标准的平均精度均值(mAP)指标来评估模型:
mAP@0.50:在单个 IoU 阈值 0.50 下的 mAP;
mAP@0.75:在更严格的 IoU 阈值 0.75 下的 mAP;
mAP@0.50:0.95:在从 0.50 到 0.95、步长为 0.05 的多个 IoU 阈值下计算的平均 mAP;
mAP(small):根据 COCO 标准,特指面积小于 32×3232 \times 3232×32 像素的小目标的 mAP@0.50。
用于整体模型评估的最终 mAP 值定义为所有目标类别平均精度(AP)的均值:
AP=∫01P(R)dR,mAP=∑i=1NclsAPNclsAP=\int_{0}^{1}P\big(R\big)d R,\mathsf{m A P}=\frac{\sum_{i=1}^{N_{\mathrm{cls}}}A P}{N_{cls}}AP=∫01P(R)dR,mAP=Ncls∑i=1NclsAP
其中 NclsN_{cls}Ncls 表示类别数量。此外,更高的 F1 分数表明检测模型的鲁棒性更强,其定义如下:
F1=2×P×RP+RF_{1}=2\times\frac{P\times R}{P+R}F1=2×P+RP×R
另外,我们以 FPS(每秒帧数)报告推理速度。除非另有说明,所有指标均在测试集上计算。
4.3. 实验设置
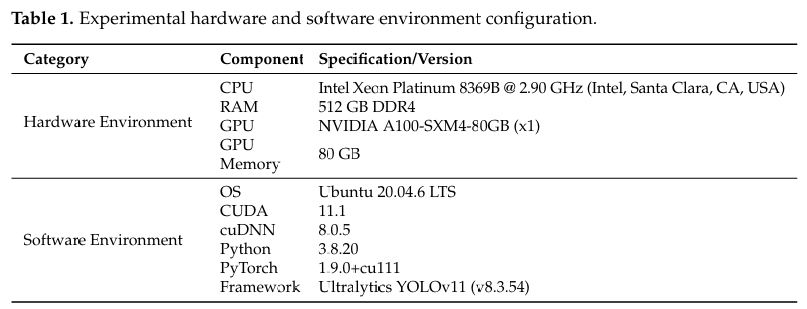
如表 1 所示,硬件环境由一块 NVIDIA A100—SXM4-80 GB GPU(NVIDIA, Santa Clara, CA, USA)组成。软件环境运行在 Ultralytics 8.3.54 Python—3.8.20 torch—1.9.0 + cu111 上。我们采用 SGD 算法进行端到端网络优化,超参数配置如下:初始学习率(lro)为 0.01,最终学习率(lrf)为 0.01,批大小为 161616,图像尺寸(imgsz)为 640,训练 300 个周期,8 个工作进程。
4.4. 实验结果
表 2-4 分别展示了 YOLOv11-OBB 和 MS-YOLOv11-OBB 模型在 DIOR-R 和 DOTA 数据集上的性能指标。通过分析模型在 DIOR-R 数据集不同类别上的表现,我们观察到改进后的模型在检测小目标方面取得了显著成果。具体而言,对于储罐(Storage Tank)和车辆(Vehicle)等小目标类别,模型的 mAP50 值分别达到了 85.87% 和 81.13%。这些结果表明,即使在处理小而具有挑战性的目标时,模型也能保持高检测精度。此外,所有类别的平均 mAP50 达到了 0.8833,进一步验证了该模型卓越的整体性能。此外,所有类别的 mAP50 均超过 69.61%。
为了与原始 YOLOv11 进一步比较并验证 MS-YOLOv11 的鲁棒性,我们在 DOTA 和 DIOR-R 数据集上进行了对比实验。结果表明,我们的方法表现更佳,改进后的 MS-YOLOv11-OBB 模型在 DIOR-R 数据集上的召回率(R)、F1 分数和 mAP 均有整体提升。与原始 YOLOv11 相比,MS-YOLOv11 的平均 P、R、F1 和 mAP50 分别提高了 0.22%、3.57%、2.32% 和 2.58%。值得注意的是,对于水坝(Dam)类别,原始 YOLOv11 的 mAP 仅为 56.61%,而 MS-YOLOv11 在储罐(Storage Tank)、船舶(Ship)和车辆(Vehicle)等类别上也实现了高精度。最后,在 DOTA 数据集上,所提出的 MS-YOLOv11 与原始 YOLOv11 相比,P、R、F1 和 mAP 分别提高了 2.75%、1.98%、2.19% 和 3.13%。从这些比较中,我们可以初步得出结论:MS-YOLOv11 在检测各种遥感目标方面表现更好,在精度和准确性上均优于原始 YOLOv11。
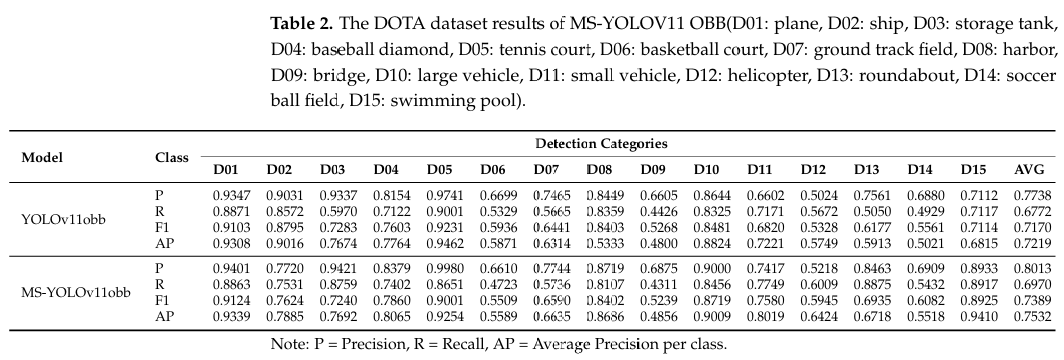
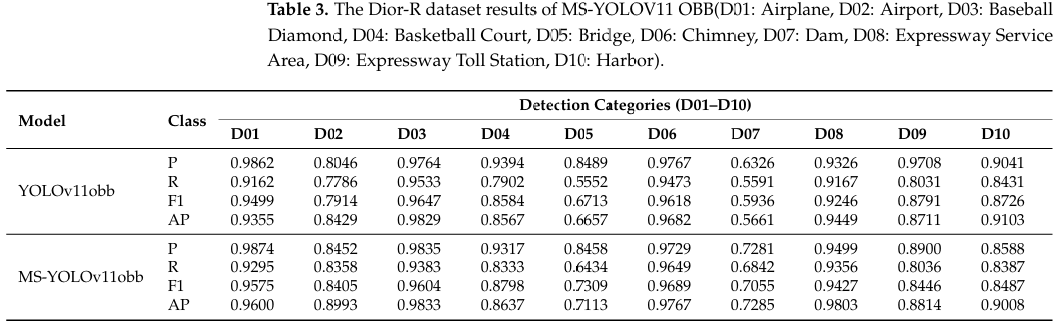
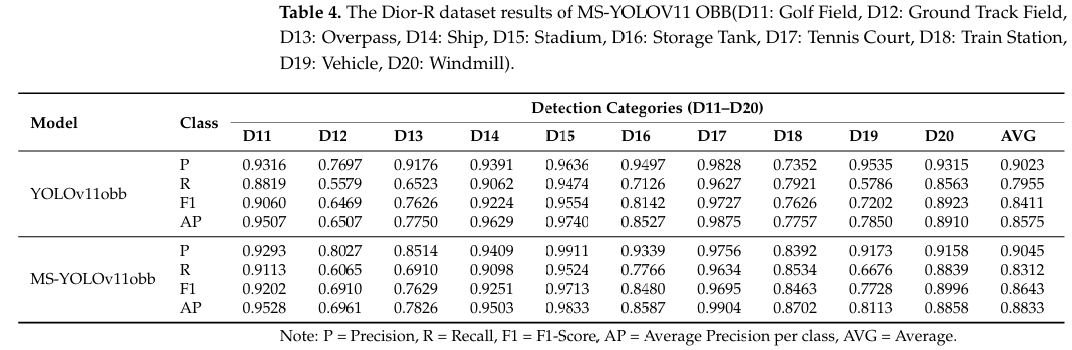
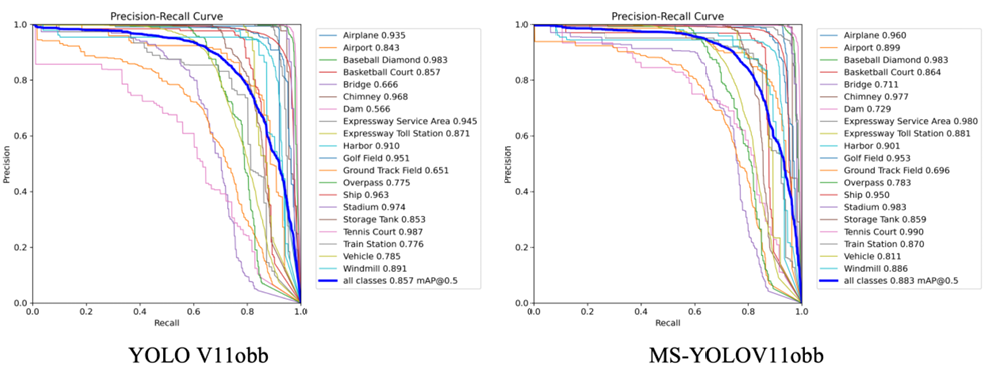
图 6 展示了两个模型的精确率-召回率(P-R)曲线,直观地反映了在不同置信度阈值下精确率与召回率之间的权衡。曲线趋势表明,MS-YOLO V11obb 的 P-R 曲线更平滑,更接近图的右上角,并且随着召回率的增加,精确率下降得更慢。这表明 MS-YOLO V11obb 在不同置信度阈值下保持了更好的性能,表现出更高的稳定性和准确性。
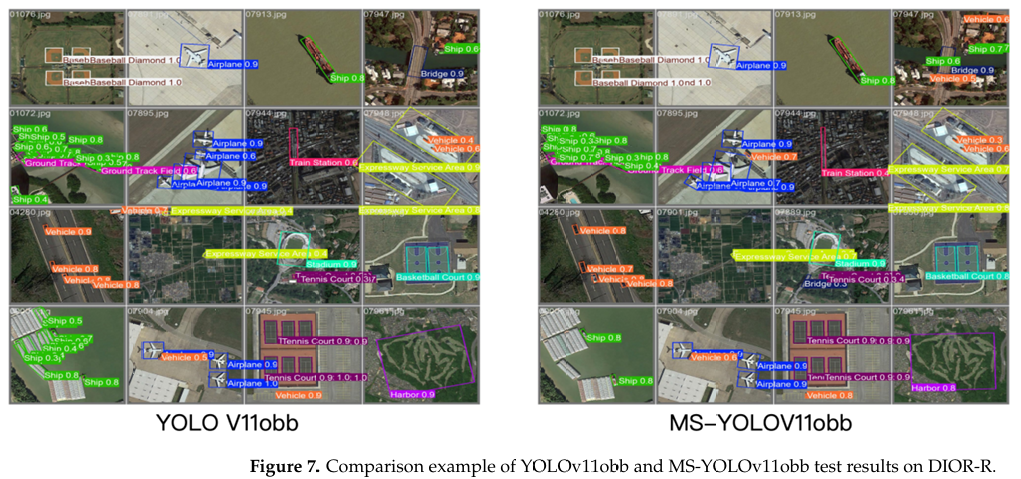
最后,为了直观地展示 MS-YOLOv11 的检测性能,我们在 DIOR-R 数据集上展示了 MS-YOLOv11 和 YOLOv11 的一些检测结果,如图 7 所示。YOLOv11 存在不同程度的漏检和误检,而 MS-YOLOv11 解决了这些问题。特别是在多个目标对象之间存在显著重叠时,MS-YOLOv11 的边界框预测更为准确。这进一步表明,我们的改进增强了原始 YOLO 的性能,有助于提高遥感目标提取的准确性。
4.5. 消融实验
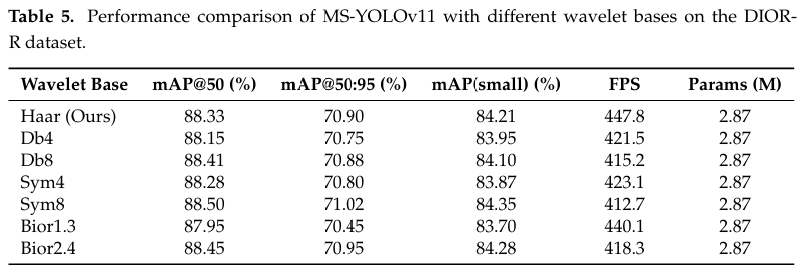
在本工作中,我们采用 Haar 小波变换是因为其高效和简洁,尽管我们的方法对基的选择是无关的,其他基也可以使用,但会增加计算需求。为了进一步验证 Haar 小波的选择并探索不同频域变换的影响,我们在相同的实验设置下与各种小波基进行了对比实验。如表 5 所示,虽然 Sym8 和 Bior2.4 等更复杂的小波由于其更高的正则性和更好的纹理表示能力,取得了有竞争力的精度,但 mAP 的差异微乎其微(<0.5%)。至关重要的是,Haar 小波在推理速度(FPS)方面表现出显著优势,远超其他基。这与我们为实际应用实现精度和效率最佳平衡的设计原则相一致。因此,我们得出结论,Haar 小波是 MS-YOLOv11 中 WTConv 模块最合适的选择。
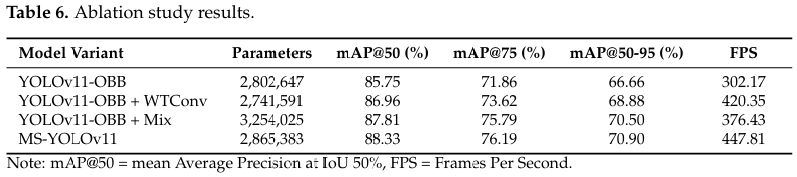
根据表 6 所示的消融研究结果,我们分析了 MS-YOLOv11 模型中不同组件的贡献。通过在骨干网络中局部增强 WTConv 模块,我们将 mAP 从 85.75% 提高到 86.96%,同时由于 WTConv 模块替换了重复使用的 C3K2 模块,参数数量减少了约 61,591,实现了 1.21% 的精度提升。当独立地将颈部网络替换为所提出的混合结构块时,mAP 从 85.75% 增加到 87.81%(提升了 2.06%)。总体而言,在基本保持参数数量不变的情况下,MS-YOLOv11 将 FPS 从 302.17 提高到 447.81,mAP 比原始 YOLOv11 高出 2.58%,并且 mAP@75 和 mAP@50-95 也分别提高了 4.33% 和 4.24%。这些结果证明了 MS-YOLOv11 对原始 YOLOv11 性能的有效增强。
4.6. 与其他检测模型的比较
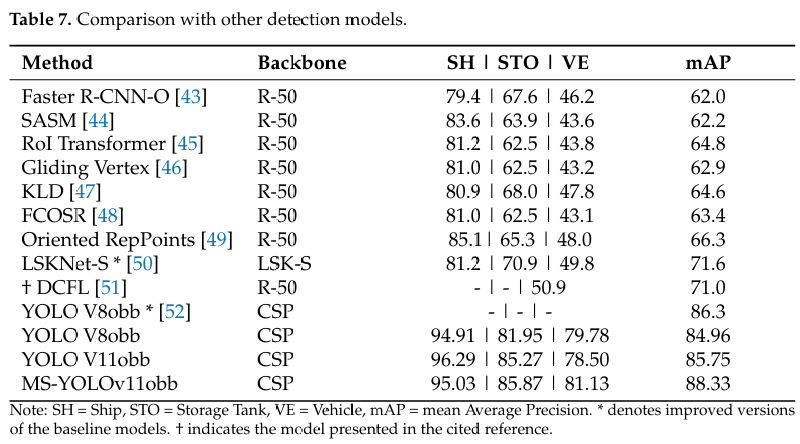
为了验证所提出的 MS-YOLOv11 的优越性,我们在 DIOR-R 数据集上与几种具有代表性的检测方法进行了全面比较,包括基线 YOLOv11、YOLOv8、经典定向目标检测器(Rotated Faster R-CNN、Rotated RetinaNet、RoI Transformer、Gliding Vertex、AOPG、GGHL、Oriented RepPoints)以及最先进的方法(LSK-S*, DCFL)。如表 7 所示,经典方法在遥感场景下的表现普遍不佳,mAP 值在 62.0% 到 66.3% 之间。值得注意的是,MS-YOLOv11 取得了最高的 mAP 88.33%,优于 YOLOv11 (85.75%) 和 YOLOv8 (84.96%),并显著超越了所有其他方法。对于小目标类别——船舶(SH)、储罐(STO)和车辆(VE)——MS-YOLOv11 的检测精度分别达到了 95.03%、85.87% 和 81.13%,显示出相对于竞争方法的一致优势。这些结果证实了 MS-YOLOv11 不仅提升了整体检测性能,而且在小目标检测方面表现出卓越的能力,验证了我们架构改进的有效性。
得益于 WTConv 模块利用二维 Haar 小波变换对输入图像进行多级分解,它在提取全局和细节特征的同时扩展了感受野。其次,网络进一步引入了混合结构块模块,以增强小目标和多尺度特征提取能力,获取的多尺度特征最终通过特征融合和残差连接进行优化。MS-YOLOv11 在遥感目标检测中表现出更高的适应性和优越的检测性能,有效地解决了漏检和误检问题。同时,在速度方面,MS-YOLOv11 相比 YOLOv11 实现了 145.64 FPS 的提升。此外,未来的研究可以整合多源遥感数据,并采用领域自适应学习等技术,以进一步提高算法的准确性和泛化能力。
5. 结论
所提出的 MS-YOLOv11 算法通过集成带有二维 Haar 小波变换的 WTConv 模块和混合结构块模块,显著改善了遥感图像中的小目标检测。WTConv 模块通过多级分解扩展感受野,同时联合提取全局和局部特征,而混合结构块则增强了多尺度特征融合。实验结果表明,MS-YOLOv11 在 DIOR-R 和 DOTA 数据集上均取得了更高的检测精度,mAP 分别提升了 2.58% 和 3.13%。在储罐(Storage Tank)小目标类别上的检测性能显著提升,从 78.50% 增加到 81.13%,提高了 2.63%。与经典算法(如 Rotated Faster R-CNN)和原始 YOLOv11 相比,该模型显著减少了漏检和误检,并提供了更精确的边界框预测。未来的工作将侧重于整合多源遥感数据和领域自适应学习,以进一步增强算法在复杂场景中的泛化能力。
