P7073 [CSP-J2020] 表达式

题目传送门

前言：树形数据结构+大模拟，作为2020年的T3甚至要比T4还要难，调了好久，CSP-J中不多见的达到了100多行的代码，非常炸裂。

思路：

本题总体方向主要是借助树形数据结构与栈来进行建树，然后对整棵树进行预处理求值，然后标记该节点是否会影响根节点的值，并进行临时修改的求值。本思路主要分为三个部分

1. 建树：

首先这部分是本题中最重要的一部分，我们通过将表达式转换为树形数据结构再求值会大大降低时间复杂度，建树的部分主要通过栈与结构体数组所表示的树来进行对于表达式的建模，而我们根据样例一可以构建出如下一棵树（如图）：

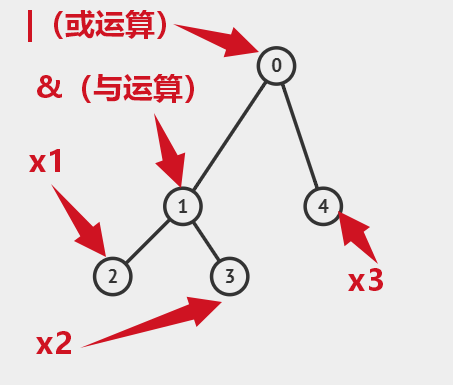
因此，我们可以按照运算符与数字的区别分成以下三种情况：

1. 如果表达式当前遍历到的东西是操作数的话：将操作数的编号存入栈
2. 如果表达式当前遍历到的是一元运算符（！取反运算），那么取出一个栈顶元素并弹出，并将栈顶元素作为当前节点的左孩子（指编号），然后将当前运算符的编号存入栈中（为避免与操作数的编号冲突，我们规定将运算符的编号从n+1开始）
3. 如果表达式当前遍历到的是二元运算符（& 与运算，| 或运算），那么先取出一个栈顶元素并弹出，接着再取出一个栈顶元素并弹出，将第一个栈顶元素作为右孩子，将第二个栈顶元素作为左孩子，与一元运算符一样，把运算符的编号存入栈中

代码如下：

    for(int i=0;i<len;i++){//建树if(s[i]=='x'){//如果当前是操作数i++;int bland=0;while(s[i]!=' '&&i<len){//获取操作数序号bland=bland*10+(s[i]-'0');i++;}st.push(bland);//将序号存入栈}else{if(s[i]==' ') continue;if(s[i]=='!'){//一元运算符处理int t=st.top();st.pop();op++;f[op+n].c='!',f[op+n].child_l=t;st.push(n+op);//将运算符的序号存入栈}else{//二元运算符处理int t1=st.top();st.pop();int t2=st.top();st.pop();// 将两个栈顶元素拿出op++;f[op+n].c=s[i],f[op+n].child_l=t2,f[op+n].child_r=t1;// 将信息存入结构体st.push(n+op);//将运算符的序号存入栈}}}

2.搜索求值：

我们直接采用DFS直接搜索，用一个数组来存储以当前节点为根节点时，当前表达式的值（注意：叶子结点即操作数的表达式的值与该操作数的原值保持一致，不需要发生改变），为后续的标记节点做铺垫（搜索应该都会吧）：

int dfs1(int x){if(x<=n) return t[x]=a[x];//如果当前序号是操作数的话，返回操作数原本的值if(f[x].c=='&'){//与运算返回值return t[x]=dfs1(f[x].child_l)&dfs1(f[x].child_r);}if(f[x].c=='|'){//或运算返回值return t[x]=dfs1(f[x].child_l)|dfs1(f[x].child_r);}if(f[x].c=='!'){//取反运算返回值return t[x]=(!dfs1(f[x].child_l));}
}

3.标记节点：

本步骤是最重要的，因为本步骤是预处理的最后一步，关于临时修改的查询操作需要借助当前步骤对于节点的标记来进行判断。

我们通过对于与运算，或运算，取反运算的运算规则可得到以下定理：

1. 如果与运算的左操作数为1，那么关于该运算的值的决定来源于右操作数
2. 如果与运算的右操作数为1，那么关于该运算的值的决定来源于左操作数
3. 如果或运算的左操作数为0，那么关于该运算的值的决定来源于右操作数
4. 如果与运算的右操作数为0，那么关于该运算的值的决定来源于左操作数
5. 对于取反运算，如果该取反运算对于距离本运算最近的二元运算符有影响的话，那么该运算的值来源于左操作数

通过以上规则，我们可以通过对于每个节点的标记得出，每个节点是否会对于根节点的值做出影响

标记代码：

void dfs2(int x){if(x==h){//如果当前节点是根节点，标记为1vis[x]=1;}if(x<=n){//叶子节点不在递归return ;}int tu_l=f[x].child_l,tu_r=f[x].child_r;//左孩子与右孩子int c=f[x].c;if(c=='&'){if(t[tu_l]&&vis[x]){vis[tu_r]=1;if(tu_r>n) dfs2(tu_r);}if(t[tu_r]&&vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}else if(c=='|'){if(!t[tu_l]&&vis[x]){vis[tu_r]=1;if(tu_r>n) dfs2(tu_r);}if(!t[tu_r]&&vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}else if(c=='!'){if(vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}return ;
}

AC CODE:

#include<bits/stdc++.h>
using namespace std;
int h;
int a[1000005];
int n;
string s;
stack<int> st;//用于建树的栈
int op=0;//存入序号
struct node{char c;//运算符int child_l,child_r;//左孩子和右孩子
}f[1000005];//结构体建树
int t[1000005];//存储以当前节点为根节点的值
bool vis[1000005];//存储该节点是否会影响最终值
int dfs1(int x){if(x<=n) return t[x]=a[x];//如果当前序号是操作数的话，返回操作数原本的值if(f[x].c=='&'){//与运算返回值return t[x]=dfs1(f[x].child_l)&dfs1(f[x].child_r);}if(f[x].c=='|'){//或运算返回值return t[x]=dfs1(f[x].child_l)|dfs1(f[x].child_r);}if(f[x].c=='!'){//取反运算返回值return t[x]=(!dfs1(f[x].child_l));}
}
void dfs2(int x){if(x==h){//如果当前节点是根节点，标记为1vis[x]=1;}if(x<=n){//叶子节点不在递归return ;}int tu_l=f[x].child_l,tu_r=f[x].child_r;//左孩子与右孩子int c=f[x].c;if(c=='&'){if(t[tu_l]&&vis[x]){vis[tu_r]=1;if(tu_r>n) dfs2(tu_r);}if(t[tu_r]&&vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}else if(c=='|'){if(!t[tu_l]&&vis[x]){vis[tu_r]=1;if(tu_r>n) dfs2(tu_r);}if(!t[tu_r]&&vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}else if(c=='!'){if(vis[x]){vis[tu_l]=1;if(tu_l>n) dfs2(tu_l);}}return ;
}
int main(){getline(cin,s);
//    cout<<s;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];t[i]=a[i];}int len=s.size();for(int i=0;i<len;i++){//建树if(s[i]=='x'){//如果当前是操作数i++;int bland=0;while(s[i]!=' '&&i<len){//获取操作数序号bland=bland*10+(s[i]-'0');i++;}st.push(bland);//将序号存入栈}else{if(s[i]==' ') continue;if(s[i]=='!'){//一元运算符处理int t=st.top();st.pop();op++;f[op+n].c='!',f[op+n].child_l=t;st.push(n+op);//将运算符的序号存入栈}else{//二元运算符处理int t1=st.top();st.pop();int t2=st.top();st.pop();// 将两个栈顶元素拿出op++;f[op+n].c=s[i],f[op+n].child_l=t2,f[op+n].child_r=t1;// 将信息存入结构体st.push(n+op);//将运算符的序号存入栈}}}h=st.top();//根节点int ans=dfs1(h);//第一遍搜索求值dfs2(h);//第二遍搜索标记节点是否会影响表达式的值int q;cin>>q;while(q--){//访问操作int xia;cin>>xia;if(vis[xia]){cout<<(!ans)<<'\n';}else{cout<<ans<<'\n';}}return 0;
}