EDA--三井物产商品预测挑战赛 Exploratory Data Analysis（探索性数据分析）

前言

在机器学习中，EDA 指的是 Exploratory Data Analysis（探索性数据分析），是建模前至关重要的一步。
简单说，EDA 就是通过可视化、统计分析等方法，「摸透数据的脾气」—— 比如：
数据里有多少变量？哪些是关键特征（比如商品销量预测中的「价格」「季节」）？
有没有缺失值、异常值（比如销量突然出现负数，明显不合理）？
特征之间有没有相关性（比如「促销活动」和「销量」是不是正相关）？
目标变量（比如要预测的「商品销量」）分布是怎样的（集中在某个区间，还是分散的）？
相当于给数据做「全身检查」，帮你发现数据的规律、隐藏问题或潜在价值，为后续的特征工程、模型选择打下基础。比如在三井物产商品预测竞赛中，通过 EDA 可能会发现「节假日」对商品销量影响极大，这就能成为建模时的重要特征 —— 跳过 EDA 直接建模，很可能会漏掉关键信息，导致模型效果拉垮。

任务描述与核心思路

三井物产商品预测挑战赛要预测的目标是424个价差序列的对数数以（log returns）数据存放于train_labels.csv文件中。
我们需要通过train_labels.csv解析每一个目标对应的资产以及滞后阶数。它的核心难点在于多市场交易时间不一致，假期不一致导致的数据对其问题、长期预测中的结构性断点，例如政策冲击、黑天鹅时间等等。

解决方案思路

多源数据清理、特征工程、构建价差特征、时序模型选择、鲁棒性优化等多个任务处理。

竞赛价值

• 对于升学中的金融工程、金融数学、统计学等专业有不错的实战经验。
• 求职量化投资、风控、金融科技等作为项目展示。
• 尽管赛事已经结束，但是对于求学、求职都是不容错过的项目之一，因为kaggle稀缺量化赛题！

EDA

# 导入数据
# 导入数据
path = r'C:\Users\0\Desktop\三井\\'
target_pairs = pd.read_csv(path + "target_pairs.csv")
train_labels = pd.read_csv(path + "train_labels.csv")
train = pd.read_csv(path + "train.csv")
test = pd.read_csv(path + "test.csv")

print("标的对数据维度：", target_pairs.shape)
print("训练标签数据维度：", train_labels.shape)
print("训练数据集维度：", train.shape)
print("\n训练数据集预览：")
train.head()

通过比较相邻两天的价格变化，计算出对数收益率。比如用第1天和第2天的价格算一个收益率，第2天和第3天的价格再算一个收益率，这样连续计算下去。

这种收益率计算方式在金融分析中很常用，能更准确地反映价格的实际变化情况。代码会把这些计算结果依次显示出来，方便查看每天的价格变动幅度。`

def calculate_log_return(old_price, new_price, days=1):"""计算对数收益率参数:old_price: 旧价格new_price: 新价格  days: 时间间隔（天数），默认为1返回:float: 对数收益率，如果输入无效返回None"""if days <= 0 or old_price <= 0 or new_price <= 0:return Nonereturn math.log(new_price / old_price)# 优化后的计算方式
def calculate_returns_optimized(price_series, window=6):"""计算价格序列的连续收益率参数:price_series: 价格序列window: 计算窗口大小返回:list: 收益率列表"""returns = []for i in range(min(window, len(price_series) - 1)):return_val = calculate_log_return(price_series.iloc[i], price_series.iloc[i+1])returns.append(return_val)print(f"第{i+1}天到第{i+2}天的收益率: {return_val:.6f}")return returns# 使用优化函数
print("📈 US_Stock_VT 连续收益率计算：")
vt_returns = calculate_returns_optimized(train["US_Stock_VT_adj_close"])

我自己对股票和大宗商品资产只做了一点研究。我认为，由于基本面因素（各种全球话题、新闻和趋势），股票价格和类似价格波动很大。 我或多或少已经放弃了这样一种想法，即机器学习模型可以整合所有这些基础知识来进行预测（也许将来会有可能……但我不知道会发生什么）。 所以，我在这里能做的就是根据它们自己的价格走势以及其他价格的走势来预测未来的价格。

我想尝试的想法是为低波动性条件建立一个模型，为高波动性条件构建另一个模型。因为我认为这两个人最终只会成为彼此的噪音。当然，如果价格趋势本身在波动后发生变化，那么这种策略就会崩溃。

就目前而言，关于价格趋势，我会以资产自身的价格为主要特征，当波动性上升时切换到“高波动性模型”，一旦它平静下来，就切换回原始模型。此外，由于有400多个项目需要预测，将它们分组或缩小到仅相关的项目也可能是一种方法。

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号def plot_correlation_heatmap(data, figsize=(20, 18), title="数据集相关性热力图", cmap="RdBu_r", annot=False, save_path=None):"""绘制相关性热力图参数:data: 输入数据框figsize: 图形尺寸title: 图表标题cmap: 颜色映射annot: 是否在热力图上显示数值save_path: """# 计算相关性矩阵corr_matrix = data.corr()# 创建图形plt.figure(figsize=figsize)# 绘制热力图sns.heatmap(corr_matrix, mask=mask if annot else None,  # 如果显示数值，隐藏上三角避免重复cmap=cmap,center=0,  # 以0为中心annot=annot,  # 控制是否显示数值fmt=".2f",   # 数值格式annot_kws={"size": 8},  # 数值字体大小cbar_kws={"shrink": 0.8},  # 颜色条设置square=True,  # 保持单元格为正方形linewidths=0.5)  # 单元格间线宽# 设置标题和标签plt.title(title, fontsize=16, fontweight='bold', pad=20)plt.xticks(rotation=45, ha='right', fontsize=10)plt.yticks(fontsize=10)# 调整布局plt.tight_layout()# 使用优化后的函数
print("📊 正在计算相关性矩阵...")
correlation_matrix = plot_correlation_heatmap(data=train,figsize=(25, 22),title="训练数据集特征相关性热力图",cmap="coolwarm",annot=False,  # 数据量大时不建议显示数值save_path=None  
)# 显示相关性统计信息
print(f"\n📈 相关性统计信息:")
print(f"数据集形状: {train.shape}")

plt.figure(figsize=(30,30))
sns.heatmap(train_labels.corr(), cmap="coolwarm")
plt.show()

找出价格波动特别大的时期。

它从数据中挑选了几个代表性的资产，对每个资产都计算其价格波动情况。具体做法是看每20天的价格变化幅度，然后找出那些波动特别剧烈的时期——也就是波动幅度超过90%其他时间段的情况。

在图表上，这些高波动时期会用红色阴影标出来，让人一眼就能看出哪些时候市场特别不稳定。同时还会显示波动率的统计数字，比如平均波动幅度、最大波动幅度等。

这样就能清楚了解各个资产在什么时间段出现了异常波动，帮助识别市场的风险时期。

# 选择要分析的目标列
plot_target_columns = [train.columns[1],    # 第2列train.columns[100],  # 第101列  train.columns[200],  # 第201列train.columns[300],  # 第301列train.columns[400]   # 第401列
]print(f"📊 开始分析 {len(plot_target_columns)} 个目标列的高波动区间...")for i, target_col in enumerate(plot_target_columns, 1):print(f"\n🔍 正在处理第 {i}/{len(plot_target_columns)} 个列: {target_col}")# 计算滚动波动率（20日标准差）rolling_volatility = train[target_col].rolling(window=20, min_periods=10).std()# 计算波动率阈值（90%分位数）volatility_threshold = rolling_volatility.quantile(0.90)# 识别高波动区间（波动率超过阈值）high_volatility_periods = rolling_volatility > volatility_threshold# 创建图形fig, ax = plt.subplots(figsize=(14, 6))# 绘制价格走势线sns.lineplot(x=train.index, y=train[target_col], ax=ax, linewidth=1.2, color='blue', label='价格走势')# 标记高波动区间high_vol_groups = pd.Series(high_volatility_periods).groupby((high_volatility_periods != high_volatility_periods.shift()).cumsum())high_vol_count = 0for group_id, group_data in high_vol_groups:if group_data.iloc[0]:  # 只处理高波动区间high_vol_count += 1ax.axvspan(group_data.index[0], group_data.index[-1], alpha=0.2, color="red", label='高波动区间' if high_vol_count == 1 else "")# 设置图表属性ax.set_title(f'{target_col} - 价格走势与高波动区间识别\n'f'(波动率阈值: {volatility_threshold:.4f}, 高波动区间数: {high_vol_count})', fontsize=14, fontweight='bold', pad=15)ax.set_xlabel('时间索引', fontsize=12)ax.set_ylabel('价格', fontsize=12)ax.legend(loc='upper right')ax.grid(True, alpha=0.3)# 添加波动率信息文本框textstr = f'''波动率统计:
均值: {rolling_volatility.mean():.4f}
最大值: {rolling_volatility.max():.4f}
阈值(90%): {volatility_threshold:.4f}'''ax.text(0.02, 0.98, textstr, transform=ax.transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.8))plt.tight_layout()plt.show()# 输出统计信息total_periods = len(high_volatility_periods)high_vol_ratio = high_volatility_periods.sum() / total_periods * 100print(f"  高波动区间占比: {high_vol_ratio:.2f}% ({high_vol_count} 个区间)")print(f"\n✅ 所有 {len(plot_target_columns)} 个目标列分析完成！")

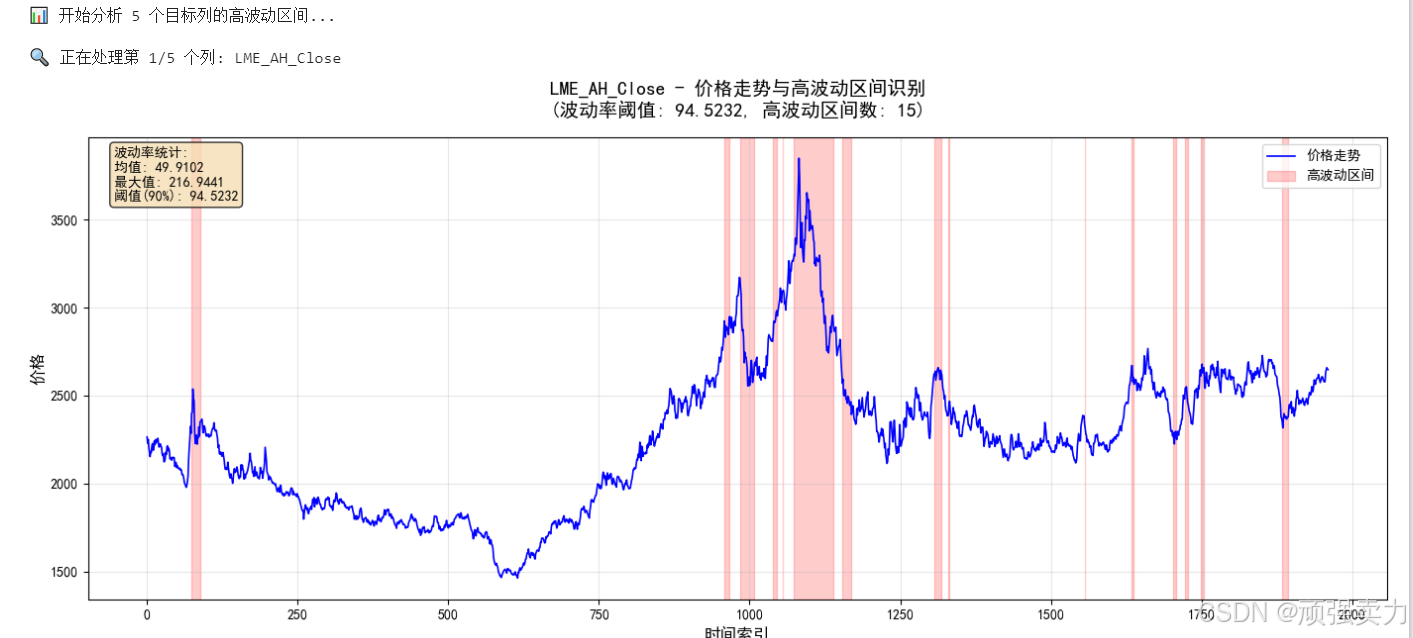
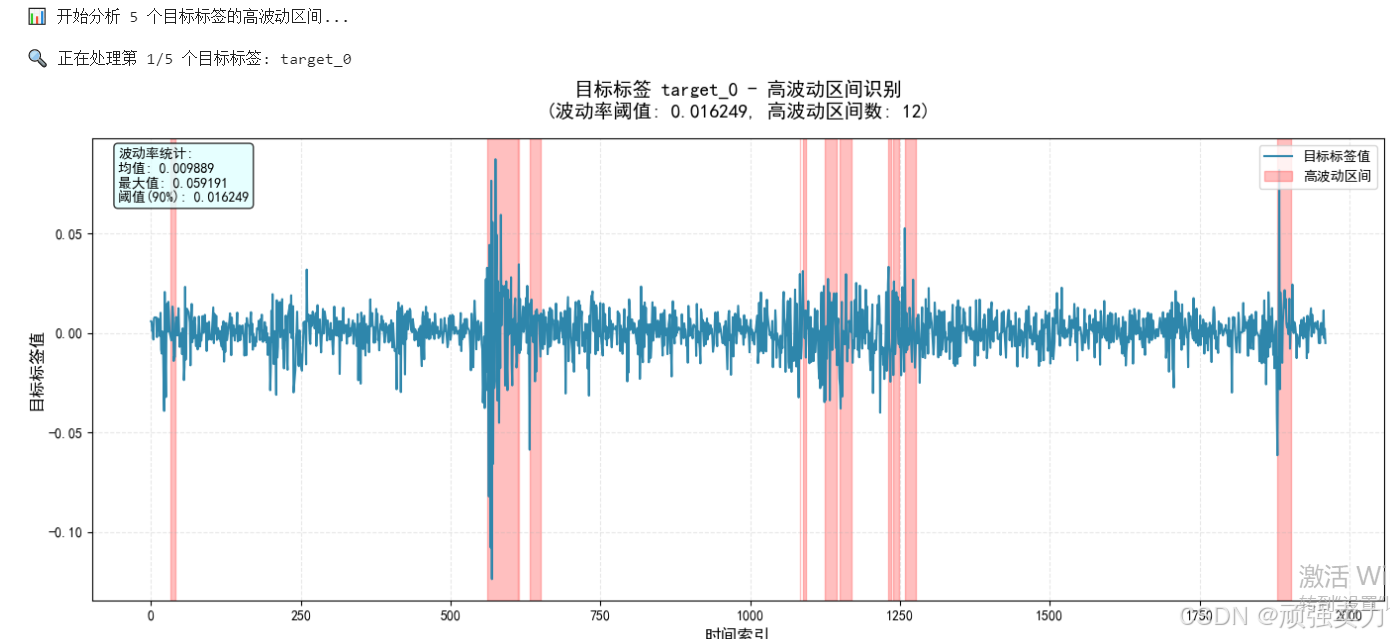
分析预测目标值的波动情况。

它从几百个预测目标中挑选了5个有代表性的，检查它们在时间序列上的波动特征。具体来说，它会找出那些波动特别剧烈的时期——也就是波动幅度超过90%其他时间段的异常波动期。

在图表上，这些高波动时期会用红色背景标出来，让人一眼就能看出预测目标在哪些时间段出现了异常变化。同时还会显示波动率的统计信息，比如平均波动幅度和阈值水平。

通过这种分析，可以了解预测目标的稳定性，识别出那些难以预测的剧烈波动时期，为建模提供参考。

# 选择要分析的目标标签列
plot_target_columns = ['target_0', 'target_100', 'target_200', 'target_300', 'target_400']print(f"📊 开始分析 {len(plot_target_columns)} 个目标标签的高波动区间...")for i, target_col in enumerate(plot_target_columns, 1):print(f"\n🔍 正在处理第 {i}/{len(plot_target_columns)} 个目标标签: {target_col}")# 计算滚动波动率（20日标准差，至少需要10个数据点）rolling_volatility = train_labels[target_col].rolling(window=20, min_periods=10).std()# 计算波动率阈值（90%分位数）volatility_threshold = rolling_volatility.quantile(0.90)# 识别高波动区间（波动率超过阈值）high_volatility_periods = rolling_volatility > volatility_threshold# 创建图形fig, ax = plt.subplots(figsize=(14, 6))# 绘制目标标签走势线sns.lineplot(x=train_labels.index, y=train_labels[target_col], ax=ax, linewidth=1.5, color='#2E86AB', label='目标标签值')# 分组识别连续的高波动区间high_vol_groups = pd.Series(high_volatility_periods).groupby((high_volatility_periods != high_volatility_periods.shift()).cumsum())# 标记高波动区间high_vol_count = 0for group_id, group_data in high_vol_groups:if group_data.iloc[0]:  # 只处理高波动区间high_vol_count += 1ax.axvspan(group_data.index[0], group_data.index[-1], alpha=0.25, color="red", label='高波动区间' if high_vol_count == 1 else "")# 设置图表属性ax.set_title(f'目标标签 {target_col} - 高波动区间识别\n'f'(波动率阈值: {volatility_threshold:.6f}, 高波动区间数: {high_vol_count})', fontsize=14, fontweight='bold', pad=15)ax.set_xlabel('时间索引', fontsize=12)ax.set_ylabel('目标标签值', fontsize=12)ax.legend(loc='upper right')ax.grid(True, alpha=0.3, linestyle='--')# 添加统计信息文本框textstr = f'''波动率统计:
均值: {rolling_volatility.mean():.6f}
最大值: {rolling_volatility.max():.6f}
阈值(90%): {volatility_threshold:.6f}'''ax.text(0.02, 0.98, textstr, transform=ax.transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle='round', facecolor='lightcyan', alpha=0.8))plt.tight_layout()plt.show()# 输出详细统计信息total_periods = len(high_volatility_periods)valid_periods = rolling_volatility.notna().sum()high_vol_count_total = high_volatility_periods.sum()high_vol_ratio = (high_vol_count_total / valid_periods * 100) if valid_periods > 0 else 0print(f"  有效数据点: {valid_periods}/{total_periods}")print(f"  高波动区间占比: {high_vol_ratio:.2f}% ({high_vol_count_total} 个数据点)")print(f"  连续高波动区间数: {high_vol_count}")print(f"\n✅ 所有 {len(plot_target_columns)} 个目标标签分析完成！")# 汇总统计
print(f"\n📈 目标标签高波动分析汇总:")
for target_col in plot_target_columns:vol = train_labels[target_col].rolling(20, min_periods=10).std()thr = vol.quantile(0.90)high_vol_ratio = (vol > thr).sum() / vol.notna().sum() * 100print(f"  {target_col}: 高波动占比 {high_vol_ratio:.2f}%")

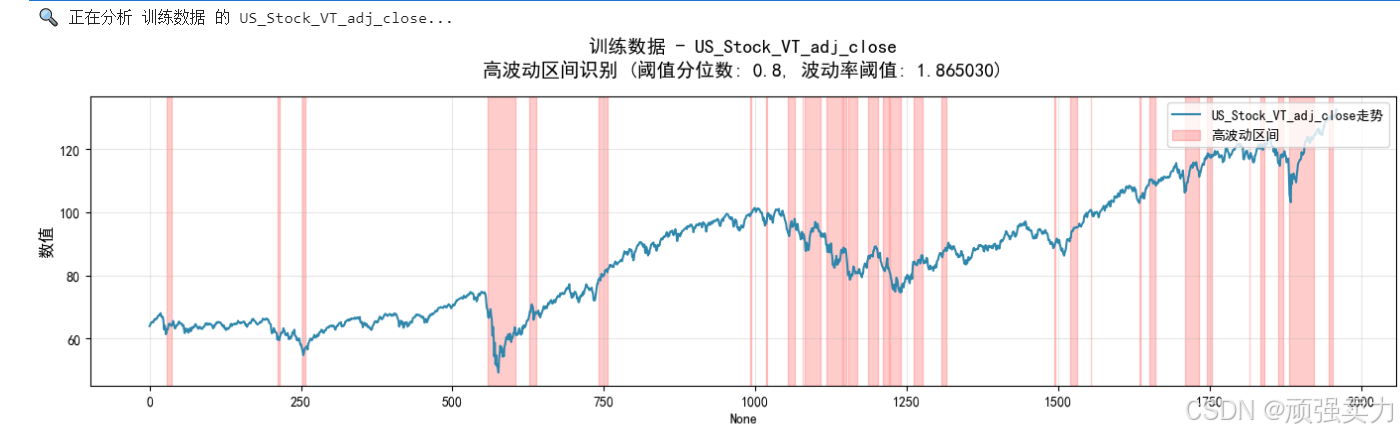
分析价格和预测目标的波动情况，找出市场特别不稳定的时期。

它分别检查了两个重要指标：一个是全球股票ETF的价格走势，另一个是预测模型的目标值。分析方法是计算每20天的价格波动幅度，然后找出那些波动特别大的时期——也就是波动幅度超过80%其他时间段的异常时期。

结果显示为上下两个图表：上面的图显示价格走势，用红色阴影标出高波动时期；下面的图显示波动率本身的变化，用一条红色虚线标明阈值。

通过这种分析，可以清楚看到市场在哪些时间段出现了异常波动，帮助识别风险时期和潜在的投资机会。

def plot_high_volatility_intervals(data, column_name, data_source, threshold_quantile=0.80, window=20, min_periods=10, figsize=(14, 6)):"""绘制时间序列的高波动区间参数:data: 数据源column_name: 列名data_source: 数据来源描述threshold_quantile: 波动率阈值分位数window: 滚动窗口大小min_periods: 最小计算周期figsize: 图形尺寸"""print(f"🔍 正在分析 {data_source} 的 {column_name}...")# 计算滚动波动率volatility = data[column_name].rolling(window=window, min_periods=min_periods).std()# 计算波动率阈值threshold = volatility.quantile(threshold_quantile)# 识别高波动区间high_vol = volatility > threshold# 创建图形fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(figsize[0], figsize[1] + 2))# 上子图：价格/数值走势与高波动区间sns.lineplot(x=data.index, y=data[column_name], ax=ax1, linewidth=1.5, color='#2E86AB', label=f'{column_name}走势')# 标记高波动区间high_vol_count = 0high_vol_groups = pd.Series(high_vol).groupby((high_vol != high_vol.shift()).cumsum())for _, group in high_vol_groups:if group.iloc[0]:  # 只处理高波动区间high_vol_count += 1ax1.axvspan(group.index[0], group.index[-1], alpha=0.2, color="red", label='高波动区间' if high_vol_count == 1 else "")ax1.set_title(f'{data_source} - {column_name}\n'f'高波动区间识别 (阈值分位数: {threshold_quantile}, 波动率阈值: {threshold:.6f})', fontsize=14, fontweight='bold', pad=15)ax1.set_ylabel('数值', fontsize=12)ax1.legend(loc='upper right')ax1.grid(True, alpha=0.3)# 下子图：波动率走势ax2.plot(volatility.index, volatility, linewidth=1.5, color='#FF6B6B', label='波动率')ax2.axhline(y=threshold, color='red', linestyle='--', linewidth=2, label=f'高波动阈值 ({threshold_quantile*100}%分位数)')ax2.set_ylabel('波动率', fontsize=12)ax2.set_xlabel('时间索引', fontsize=12)ax2.legend(loc='upper right')ax2.grid(True, alpha=0.3)ax2.set_title('波动率走势与阈值线', fontsize=12, pad=10)plt.tight_layout()plt.show()# 输出统计信息valid_periods = volatility.notna().sum()high_vol_periods = high_vol.sum()high_vol_ratio = (high_vol_periods / valid_periods * 100) if valid_periods > 0 else 0print(f"📊 {column_name} 波动分析统计:")print(f"  - 有效数据点: {valid_periods}")print(f"  - 高波动数据点: {high_vol_periods} ({high_vol_ratio:.2f}%)")print(f"  - 连续高波动区间数: {high_vol_count}")print(f"  - 波动率范围: {volatility.min():.6f} ~ {volatility.max():.6f}")print(f"  - 波动率阈值({threshold_quantile*100}%分位数): {threshold:.6f}")print()# 分析股票价格的高波动区间
plot_high_volatility_intervals(data=train,column_name="US_Stock_VT_adj_close",data_source="训练数据",threshold_quantile=0.80,window=20,min_periods=10
)# 分析目标标签的高波动区间
plot_high_volatility_intervals(data=train_labels,column_name="target_0",data_source="训练标签",threshold_quantile=0.80,window=20,min_periods=10
)print("✅ 高波动区间分析完成！")

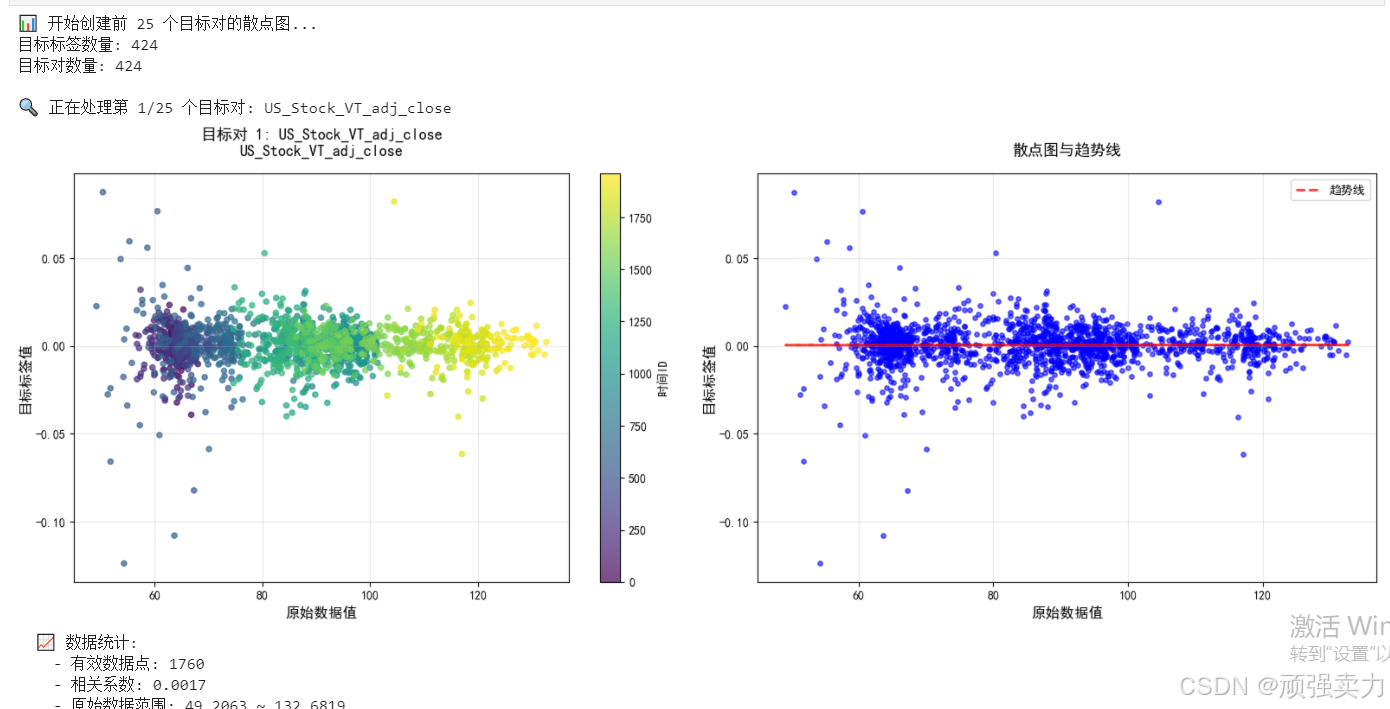
分析不同资产组合与预测目标之间的关系。

它从几百个资产组合中挑选了25个来分析，每个组合要么是两个资产的价差（比如铜价减锌价），要么是单个资产的价格。然后画出散点图，来看这些原始数据与对应的预测目标值之间有什么关系。

左边图表用颜色表示时间顺序，可以观察关系是否随时间变化；右边图表加了趋势线，能更清楚地看出整体关系方向。还会计算相关系数，量化这种关系的强弱。

通过这种分析，可以了解哪些资产组合与预测目标关联密切，为建模提供线索，比如发现某些价差变化确实能预测未来的收益差异。

def create_target_pair_plots(target_pairs, train, train_labels, num_plots=25):"""创建目标对与标签关系的散点图参数:target_pairs: 目标对数据框train: 训练数据train_labels: 训练标签num_plots: 要绘制的图形数量"""# 获取目标标签列表（排除第一列）target_label_list = train_labels.head(1).columns.to_list()[1:]print(f"📊 开始创建前 {num_plots} 个目标对的散点图...")print(f"目标标签数量: {len(target_label_list)}")print(f"目标对数量: {len(target_pairs)}")# 限制绘制的数量num_plots = min(num_plots, len(target_pairs), len(target_label_list))for i, target_pair in enumerate(target_pairs["pair"].to_list()[:num_plots]):print(f"\n🔍 正在处理第 {i+1}/{num_plots} 个目标对: {target_pair}")# 创建绘图数据框df_plot = pd.DataFrame()df_plot["date_id"] = train["date_id"]# 解析目标对并计算原始数据parts_list = [p.strip() for p in target_pair.split("-")]if len(parts_list) == 2:# 计算两个特征的差值绝对值df_plot["raw_data"] = abs(train[parts_list[0]] - train[parts_list[1]])data_description = f"{parts_list[0]} - {parts_list[1]} (绝对值)"else:# 使用单一特征df_plot["raw_data"] = train[parts_list[0]]data_description = parts_list[0]# 添加对应的目标标签current_target = target_label_list[i]df_plot["target"] = train_labels[current_target]# 移除缺失值df_plot_clean = df_plot.dropna()if len(df_plot_clean) == 0:print(f"  ⚠️  {target_pair} 无有效数据，跳过")continue# 创建图形fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))# 左图：散点图（按时间着色）scatter = ax1.scatter(x=df_plot_clean["raw_data"], y=df_plot_clean["target"], c=df_plot_clean["date_id"], cmap="viridis", alpha=0.7,s=20)ax1.set_xlabel('原始数据值', fontsize=12)ax1.set_ylabel('目标标签值', fontsize=12)ax1.set_title(f'目标对 {i+1}: {target_pair}\n{data_description}', fontsize=13, fontweight='bold', pad=15)ax1.grid(True, alpha=0.3)# 添加颜色条cbar = plt.colorbar(scatter, ax=ax1)cbar.set_label('时间ID', fontsize=10)# 右图：添加趋势线和统计信息ax2.scatter(x=df_plot_clean["raw_data"], y=df_plot_clean["target"], alpha=0.6, s=15, color='blue')# 计算并绘制趋势线if len(df_plot_clean) > 1:z = np.polyfit(df_plot_clean["raw_data"], df_plot_clean["target"], 1)p = np.poly1d(z)ax2.plot(df_plot_clean["raw_data"], p(df_plot_clean["raw_data"]), "r--", alpha=0.8, linewidth=2, label='趋势线')ax2.set_xlabel('原始数据值', fontsize=12)ax2.set_ylabel('目标标签值', fontsize=12)ax2.set_title('散点图与趋势线', fontsize=13, fontweight='bold', pad=15)ax2.legend()ax2.grid(True, alpha=0.3)plt.tight_layout()plt.show()# 输出统计信息correlation = df_plot_clean["raw_data"].corr(df_plot_clean["target"])print(f"  📈 数据统计:")print(f"    - 有效数据点: {len(df_plot_clean)}")print(f"    - 相关系数: {correlation:.4f}")print(f"    - 原始数据范围: {df_plot_clean['raw_data'].min():.4f} ~ {df_plot_clean['raw_data'].max():.4f}")print(f"    - 目标标签范围: {df_plot_clean['target'].min():.4f} ~ {df_plot_clean['target'].max():.4f}")print(f"\n✅ 已完成 {num_plots} 个目标对的散点图分析！")# 使用优化后的函数
create_target_pair_plots(target_pairs, train, train_labels, num_plots=25)# 额外的汇总分析
print(f"\n📋 目标对类型统计:")
pair_types = []
for target_pair in target_pairs["pair"].to_list()[:25]:parts_list = [p.strip() for p in target_pair.split("-")]if len(parts_list) == 2:pair_types.append("差值对")else:pair_types.append("单一特征")type_counts = pd.Series(pair_types).value_counts()
for type_name, count in type_counts.items():print(f"  {type_name}: {count} 个")

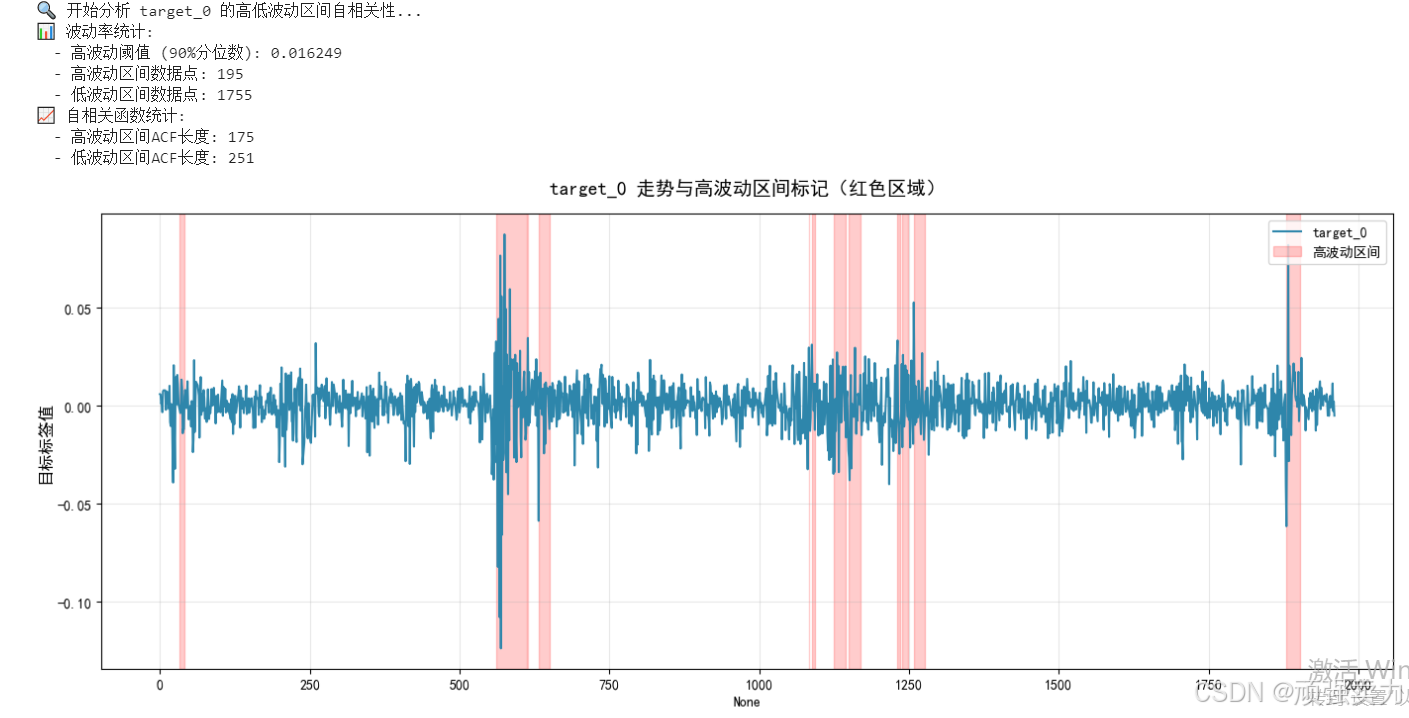
分析预测目标在不同市场状态下的记忆效应。

它把预测目标的时间序列分成两种状态：高波动时期（市场不稳定）和低波动时期（市场平稳）。然后分别计算这两种状态下数据的自相关性，也就是看今天的数据对明天、后天…有多大的预测作用。

结果显示为三个图表：第一个显示目标值走势，用红色标出高波动时期；第二个显示高波动时期的自相关情况；第三个显示低波动时期的自相关情况。通过对比，可以看出市场不稳定时和平稳时，历史数据的预测能力有什么不同。

这种分析帮助理解预测目标在不同市场环境下的行为特征，为建模提供重要参考。

def calculate_acf(x, nlags=250, drop_head=5):"""计算自相关函数(ACF)，去除前几个数据点参数:x: 输入序列nlags: 最大滞后阶数drop_head: 去除前几个数据点返回:numpy array: 自相关函数值"""x = pd.Series(x).dropna().to_numpy(float)# 检查数据是否足够if x.size <= drop_head + 1:return np.array([])# 去除前几个数据点x = x[drop_head:]# 去中心化x -= x.mean()# 计算自相关c = np.correlate(x, x, mode='full')[x.size-1:]out = c[:min(nlags + 1, c.size)]# 标准化return out / out[0] if out[0] != 0 else np.zeros_like(out)# 参数设置
window_size = 20
target_column = 'target_0'print(f"🔍 开始分析 {target_column} 的高低波动区间自相关性...")# 计算滚动波动率
volatility = train_labels[target_column].rolling(window=window_size, min_periods=window_size//2).std()# 计算高波动阈值（90%分位数）
threshold = volatility.dropna().quantile(0.90) if volatility.dropna().size else np.nan# 识别高低波动区间
if np.isfinite(threshold):high_vol = volatility.notna() & (volatility >= threshold)low_vol = volatility.notna() & ~high_vol
else:high_vol = pd.Series(False, index=volatility.index)low_vol = pd.Series(False, index=volatility.index)print(f"📊 波动率统计:")
print(f"  - 高波动阈值 (90%分位数): {threshold:.6f}")
print(f"  - 高波动区间数据点: {high_vol.sum()}")
print(f"  - 低波动区间数据点: {low_vol.sum()}")# 创建图形
fig, axes = plt.subplots(3, 1, figsize=(14, 12), sharex=False,gridspec_kw={'height_ratios': [2, 1, 1]})
ax1, ax2, ax3 = axes# (1) target_0 走势与高波动区间标记
sns.lineplot(x=train_labels.index, y=train_labels[target_column], ax=ax1, linewidth=1.5, color='#2E86AB', label=target_column)# 标记高波动区间
high_vol_count = 0
for _, group in pd.Series(high_vol).groupby((high_vol != high_vol.shift()).cumsum()):if group.iloc[0]:high_vol_count += 1ax1.axvspan(group.index[0], group.index[-1], alpha=0.2, color='red', label='高波动区间' if high_vol_count == 1 else "")ax1.set_title(f'{target_column} 走势与高波动区间标记（红色区域）', fontsize=14, fontweight='bold', pad=15)
ax1.set_ylabel('目标标签值', fontsize=12)
ax1.legend(loc='upper right')
ax1.grid(True, alpha=0.3)# 计算自相关函数
lags_required = 250
acf_high_vol = calculate_acf(train_labels.loc[high_vol, target_column], lags_required)
acf_low_vol = calculate_acf(train_labels.loc[low_vol, target_column], lags_required)print(f"📈 自相关函数统计:")
print(f"  - 高波动区间ACF长度: {len(acf_high_vol)}")
print(f"  - 低波动区间ACF长度: {len(acf_low_vol)}")# (2) 高波动区间的自相关函数
if acf_high_vol.size:ax2.plot(range(acf_high_vol.size), acf_high_vol, color='red', linewidth=2, label='高波动区间ACF')ax2.axhline(y=0, color='black', linestyle='-', alpha=0.3)# 添加置信区间（近似）ax2.axhline(y=2/np.sqrt(len(acf_high_vol)), color='gray', linestyle='--', alpha=0.5)ax2.axhline(y=-2/np.sqrt(len(acf_high_vol)), color='gray', linestyle='--', alpha=0.5)ax2.set_title('高波动区间自相关函数 (去除前5个数据点)', fontsize=13, fontweight='bold', pad=10)
ax2.set_xlabel('滞后阶数', fontsize=11)
ax2.set_ylabel('自相关系数', fontsize=11)
ax2.legend()
ax2.grid(True, alpha=0.3)# (3) 低波动区间的自相关函数
if acf_low_vol.size:ax3.plot(range(acf_low_vol.size), acf_low_vol, color='blue', linewidth=2, label='低波动区间ACF')ax3.axhline(y=0, color='black', linestyle='-', alpha=0.3)# 添加置信区间（近似）ax3.axhline(y=2/np.sqrt(len(acf_low_vol)), color='gray', linestyle='--', alpha=0.5)ax3.axhline(y=-2/np.sqrt(len(acf_low_vol)), color='gray', linestyle='--', alpha=0.5)ax3.set_title('低波动区间自相关函数 (去除前5个数据点)', fontsize=13, fontweight='bold', pad=10)
ax3.set_xlabel('滞后阶数', fontsize=11)
ax3.set_ylabel('自相关系数', fontsize=11)
ax3.legend()
ax3.grid(True, alpha=0.3)plt.tight_layout()
plt.show()# 输出详细分析结果
print(f"\n📋 分析结果总结:")
print(f"  - 检测到 {high_vol_count} 个连续高波动区间")
if acf_high_vol.size > 0 and acf_low_vol.size > 0:print(f"  - 高波动区间初期自相关: {acf_high_vol[1]:.4f} (滞后1阶)")print(f"  - 低波动区间初期自相关: {acf_low_vol[1]:.4f} (滞后1阶)")print(f"  - 高波动衰减速度: {np.mean(np.abs(acf_high_vol[:10])):.4f}")print(f"  - 低波动衰减速度: {np.mean(np.abs(acf_low_vol[:10])):.4f}")print(f"\n✅ {target_column} 自相关分析完成！")

数据预处理：处理缺失值，用前后数据填充空白

时间序列特征：

• 滞后特征：加入前几天、前几周的历史数据
• 价格变化：计算每日涨跌幅、价格变动幅度
• 滚动统计：计算移动平均线、波动率等指标

技术指标：

• RSI相对强弱指标
• 布林带
• 动量指标
• 波动率计算

跨市场特征：

• 不同资产间的价差（比如铜价减锌价）
• 资产价格比率
• 相关性分析

统计特征：

• 偏度、峰度等分布形态指标
• Z-score标准化
• 分位数统计

简单说，就是把原始的价格数据加工成各种有预测价值的指标，帮助模型更好地捕捉市场规律。比如不仅看今天股价，还看近期趋势、波动情况、与其他资产的关系等。

以上仅为三井物产商品预测挑战赛的EDA部分，如果您喜欢或者向了解更多，可以移步下面的连接，如果您仅仅想看本次竞赛解题思路，也可以移步小绿号海水三千查看《三井物产商品预测怎么冲分？优胜者的 Transformer 建模思路，全在这了》！
链接https://blog.csdn.net/weixin_48152827/article/details/153417219？spm=1001.2014.3001.5502