Week 21: 深度学习补遗：ViT Overview与手搓Multi-Head Attention

Week 21: 深度学习补遗：ViT Overview与手搓Multi-Head Attention

摘要

本周，阅读了ViT的文献以及进行了多头注意力机制的简单手搓，再次加强了对多头注意力机制与维度变化的理解，花了一定的时间解决了具体实践中维度变化理解的疑难杂症，将理论与实践进行了一定的联系，收获颇丰。

Abstract

This week, I reviewed the ViT original paper and conducted a hands-on experiment with the multi-head attention mechanism. This reinforced my understanding of how multi-head attention interacts with dimensionality changes. I spent considerable time resolving complex issues related to dimensionality in practical applications, successfully bridging theory and practice. The experience proved highly rewarding.

1. ViT概览

ViT是Vision Transformer的简称。和CNN的“利用卷积操作提取局部特征”区别，ViT的思想是，把一副图像拆成多个固定大小的块，转化为类似自然语言的Token，利用纯Transformer架构完成图像的全局建模，并且利用注意力机制进行长距离依赖关系的捕捉。

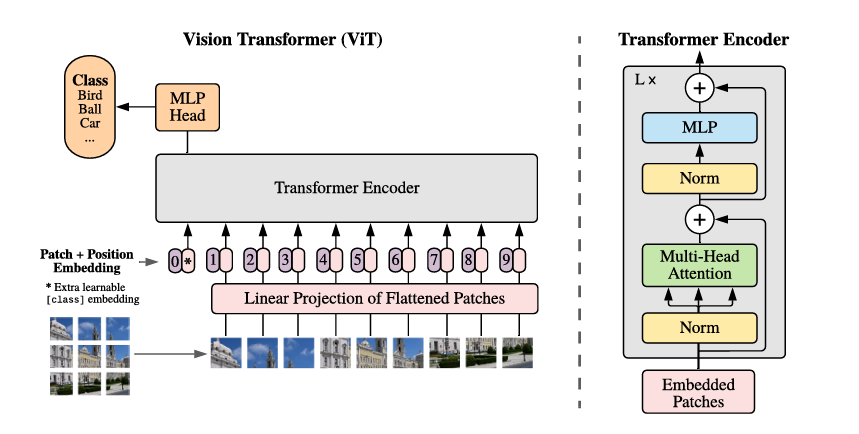
1.1 数据流

1. 将模型切分为固定大小的块（Patches）
2. 将块展平成（Flatten）向量
3. 加上位置嵌入编码（Position Embedding）
4. 进入Transformer的Encoder
5. 进入MLP头
6. 获得分类结果

1.2 Discussion

ViT作为视觉Transformer的先驱，整体结构较为简单粗暴。

对于输入图像，将其进行切块后，经线性映射层对展平的Patch进行映射后，加上位置编码，直接进入Transformer的Encoder。最后经过一个MLP Head作为Classifier，直接得到分类输出。

其主要提出了一种将图像使用Transformer进行处理的思路，但因为其Patch之间的交互完全依赖Global Attention，而网络结构又较为简单粗暴，因此效果有所局限性，特别是在纹理提取上具有一定局限性。

2. 手搓剖析 - Multi-Head Attention

本周开始，为了加深对知识点的理解，对于经典的几个网络结构开始进行手搓，并仔细分析其维度变化以及实现细节。

2.1 Code Overview

class MultiHeadAttention(nn.Module):def __init__(self, d_model, num_heads) -> None:super().__init__()self.d_model = d_modelself.num_heads = num_heads# Q, K, V projections matrixself.W_q = nn.Linear(d_model, d_model) # d_model -> d_modelself.W_k = nn.Linear(d_model, d_model)self.W_v = nn.Linear(d_model, d_model)# Output projection matrixself.W_o = nn.Linear(d_model, d_model)# Softmaxself.softmax = nn.Softmax(dim=-1) # dim=-1 means last dimensiondef forward(self, q, k, v):batch, time, dimension = q.shape # q.shape = (batch, time, d_model)n_d = self.d_model // self.num_heads # self.d_model is the dimension of the model, n_d is the dimension of each head# arranging dimensions evenly across headsq, k, v = self.W_q(q), self.W_k(k), self.W_v(v)# projecting q, k, v to target spaceq = q.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)k = k.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)v = v.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)# .view() is used to reshape the tensor without changing the data# .permute() is used to rearrange the dimensions of the tensor# view: (batch, time, d_model) -> (batch, time, num_heads, n_d)# permute: (batch, time, num_heads, n_d) -> (batch, num_heads, time, n_d)# time * n_d is the dimension of the query and key vectors# reshape for parallel computationscore = q @ k.transpose(2, 3) / math.sqrt(n_d)# @ is matrix multiplication or dot product# * is element-wise multiplication# / math.sqrt(n_d) is scaling factor to normalize the dot productmask = torch.tril(torch.ones(time, time, dtype=bool))# torch.triu() is used to create a triangular matrix with upper triangular elements# torch.tril() is used to create a triangular matrix with lower triangular elements# torch.ones() is used to create a tensor of onesscore = score.masked_fill(mask == 0, float('-inf'))score = self.softmax(score) @ vscore = score.permute(0, 2, 1, 3).contiguous().reshape(batch, time, dimension)# .contiguous() is used to make the tensor contiguous in memoryreturn self.W_o(score)

2.2 Projection Matrix 映射矩阵

self.W_q = nn.Linear(d_model, d_model) # d_model -> d_model
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)

通过在__init__中定义三个线性层W_q、W_k、W_v，代表三个权重矩阵。

本处需要注意的细节是，d_model代表模型的维度，实际上d_model > num_heads * n_d，即n_d = d_model // num_heads。所以，三个线性层W_q、W_k、W_v其实是所有注意力头都拥有的独立现行投影矩阵的组合。

2.3 计算前准备

q, k, v = self.W_q(q), self.W_k(k), self.W_v(v)
# projecting q, k, v to target spaceq = q.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)
k = k.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)
v = v.view(batch, time, self.num_heads, n_d).permute(0, 2, 1, 3)
# .view() is used to reshape the tensor without changing the data
# .permute() is used to rearrange the dimensions of the tensor
# view: (batch, time, d_model) -> (batch, time, num_heads, n_d)
# permute: (batch, time, num_heads, n_d) -> (batch, num_heads, time, n_d)# time * n_d is the dimension of the query and key vectors
# reshape for parallel computation

首先执行映射，将输入的$Q$、$K$、$V$映射到对应的空间。

然后进行reshape，将(batch, time, d_model)展开为(batch, time, num_heads, n_d)，再进行索引改变，变为(batch, num_heads, time, n_d)，这样执行矩阵乘法后维度就会变成(batch, num_heads, time, time)。

2.4 矩阵乘法与Mask

score = q @ k.transpose(2, 3) / math.sqrt(n_d)
# @ is matrix multiplication or dot product
# * is element-wise multiplication
# / math.sqrt(n_d) is scaling factor to normalize the dot productmask = torch.tril(torch.ones(time, time, dtype=bool))
# torch.triu() is used to create a triangular matrix with upper triangular elements
# torch.tril() is used to create a triangular matrix with lower triangular elements
# torch.ones() is used to create a tensor of onesscore = score.masked_fill(mask == 0, float('-inf'))
score = self.softmax(score) @ vscore = score.permute(0, 2, 1, 3).contiguous().reshape(batch, time, dimension)
# .contiguous() is used to make the tensor contiguous in memoryreturn self.W_o(score)

一些重要函数的意义在主时钟已经给出，此处不再赘述，仅叙述关键数学思路。

k.transpose(2,3)意义为转置$k$的第二、第三维度的矩阵，即从(batch, num_heads, time, n_d)变为(batch, num_heads, n_d, time)。执行score = q @ k.transpose(2, 3) / math.sqrt(n_d)后，即完成了$q$与$k$的点积，并进行了归一化。

利用torch.tril(torch.ones(time, time, dtype=bool))生成了一个下三角矩阵，维度为(time, time)，用bool类型的1填充。并利用.masked_fill(mask == 0, float('-inf'))将所有为0的元素变为负无穷-inf。

易知，在第一行只有(0,0)是1，其余都是-inf，相乘后都为-inf，这样就完成了Mask的操作，即注意力在0时刻只能看到(0,0)。

最后，执行.permute(0, 2, 1, 3)将索引恢复，并进行reshape回输入的尺寸即可输出。

总结

本周对ViT模型的文献进行了阅读，开始尝试理解模型的结构和思考其实现方式，对ViT的历史成就与局限性进行了分析和了解。同时，花费一定时间手搓了Multi-Head Attention，后续也将继续对比较重要的机制进行手搓以加强理解。本周在学习中发现数学中简要表达的某些计算过程在实践中的维度变化更加难以理解，还是需要一定的结合实践进行深入理解，本周收获较为丰富。