28~57核心原理

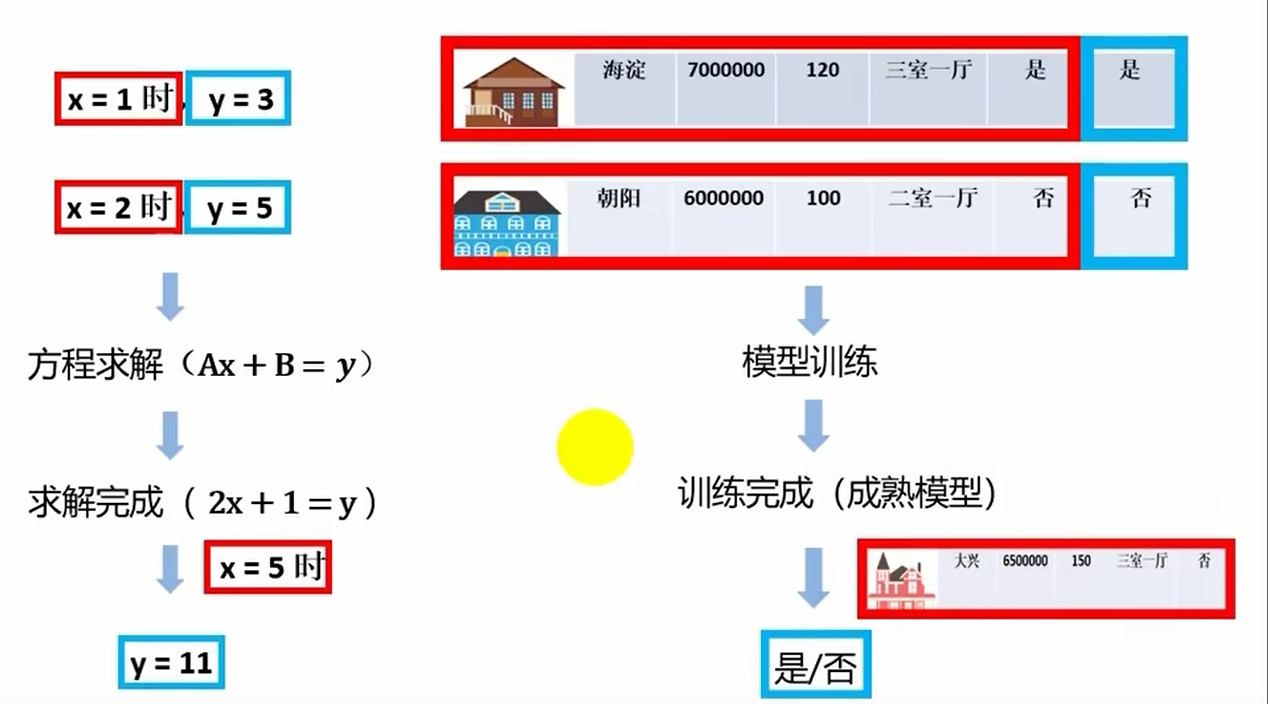
监督学习建模流程

0.总体概述

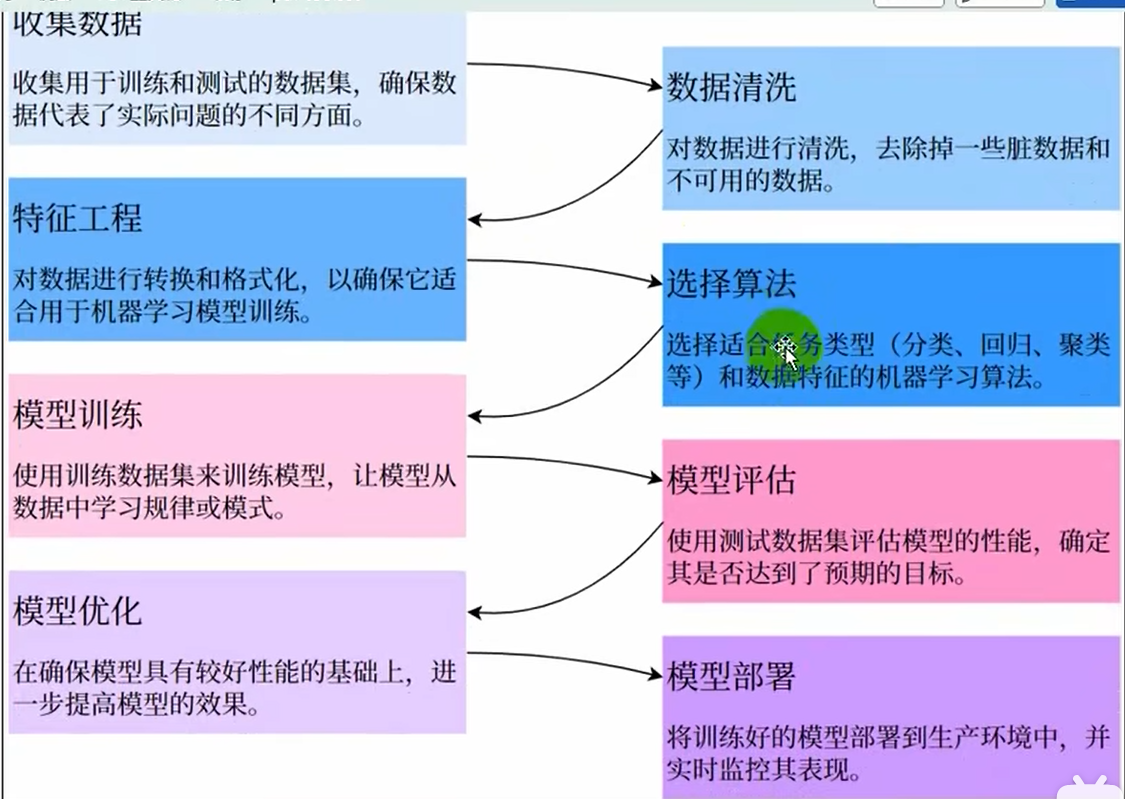
特征工程：将得到的数据转化成机器学习过程中代码可以使用的形式

1.特征工程

什么是特征工程

对原始数据的处理，转化和构造，生成新的特征或选则其中有效的特征

特征工程的内容

a.特征选择(最基本)

挑特征，不会创建新特征也不会改变数据结构

低方差过滤法：方差越大越重要，方差太小例如都是均值就没有意义了

包裹法：将特征工程放在了模型训练过程中，给模型某个特征添加一个噪声，如果这个模型结果变得很差说明这个特征非常重要，反之则不重要

b.特征转换

对数据进行数学或统计处理，使其变得更加适合模型的输入要求

独热编码(one-hot encoding):将特征的所有类别转化成不同的二进制列，用于无序类别特征

c.特征构造

基于现有的特征创造出新的，更有代表性特征

d.特征降维

当数据集特征数量非常大时，特征降维可以帮助减少计算复杂度并避免过拟合，有点像特征选择，但要保持数据本质的情况下减少特征的数量。

常用方法

特征选择

a.低方差过滤法

只看特征的方差，不关注y(标签)

import numpy as np
# 构造特征
a=np.random.randn(100) # 随机生成100个数据的ndarray数组，数组服从标准正态分布
print(np.var(a)) #np.var(a)求a的方差
b=np.random.randn(100)*0.1 #0.1X~N(0,0.01)
b=np.random.normal(5,0.1,size=100)# 随机生成100个数据的数组，服从正太分布X~N(5,0.01)
# 构造特征向量(输入数据X)
X=np.vstack((a,b)).T # vstack是将数组按行方向拼接堆叠成一个数组，要求a,b列数相同
print(X,X.shape)# 转置了所以是100*2
# 低方差过滤法
from sklearn.feature_selection import VarianceThreshold
vt=VarianceThreshold(0.01) # 设置过滤的阈值
X_filterd=vt.fit_transform(X) #适配转换后的特征
print(X_filterd,X_filterd.shape) #将b方差=0.01滤掉了，100*1

b.相关系数法

计算特征与目标变量y 或 特征之间的相关性，筛选出高相关性特征(与目标相关)或剔除冗余特征(特征间高度相关)

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 读取数据
advertising=pd.read_csv('D:\\pythoncode\\machine_learning\\ch02_base\data\\advertising.csv)
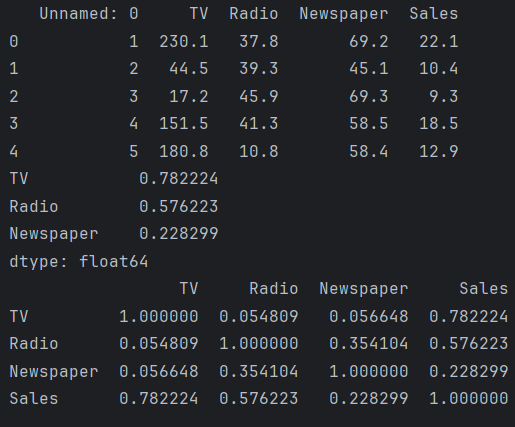
print(advertising.head()) # 第一列序号肯定和销售额无关去掉，将x,y拆分
# 数据预处理
# 去掉第一列id
'''
advertising.columns[0]获取第一列列名，返回‘Unnamed:0’
axis=1 指定操作方向为列(axis=0代表行，axis=1代表列)
inplace=True 直接修改原DataFrame,不返回副本，若设为False(默认值)，则返回删除后dataframe而不修改原数据
'''
advertising.drop(advertising.columns[0],axis=1,inplace=True)
# 去掉空值
advertising.dropna(inplace=True) #删除dataframe中所有包含缺失值的行
# 提取特征和标签(目标值)
X=advertising.drop('Sales',axis=1)
Y=advertising['Sales'] # pandas是按列存储的,代码返回一列Series,想要取第一行advertising.loc[0]
# 计算皮尔逊相关系数
print(X.corrwith(Y,method='pearson'))# corrwith()是计算Xi和Y的皮尔逊相关系数
corr_matrix=advertising.corr(method='pearson')
print(corr_matrix) # advertising内部各个特征的相关系数矩阵dataframe# 将相关系数矩阵画成热力图
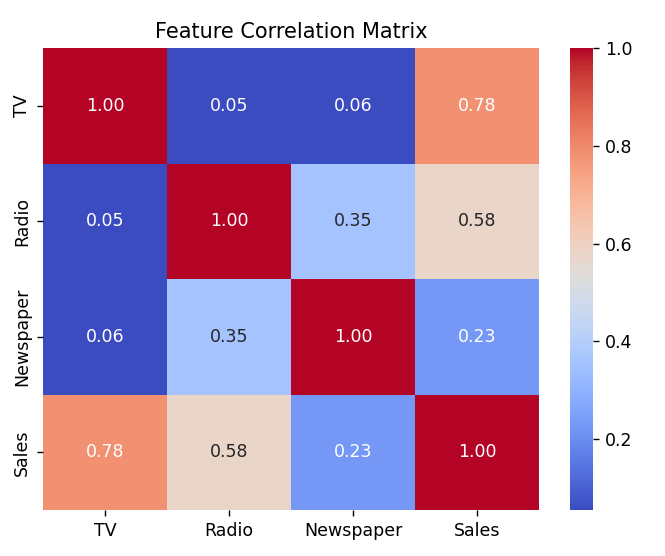
sns.heatmap(corr_matrix,annot=True,cmap='coolwarm',fmt='.2f') # annot=True是不仅显示图还显示数值
plt.title("Feature Correlation Matrix")
plt.show() # pycharm必须写，图越红说明俩相关系数越正相关

特征降维

c.PCA(主成分分析)降维

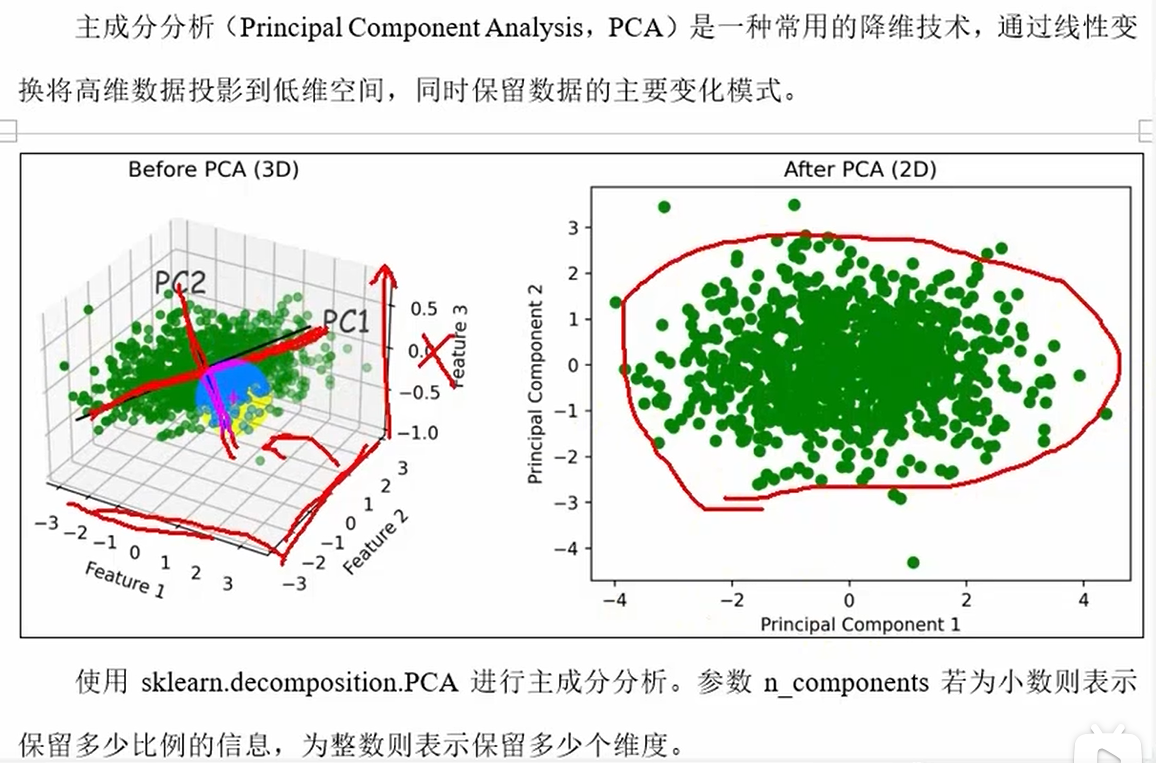
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# 生成数据
X=np.random.randn(1000,3)
# 使用PCA进行降维，将三维数据降为2维
pca=PCA(n_components=2)
X_pca=pca.fit_transform(X) # PCA类下的fit_transform适配转换方法
print(X_pca.shape)
# 可视化展示
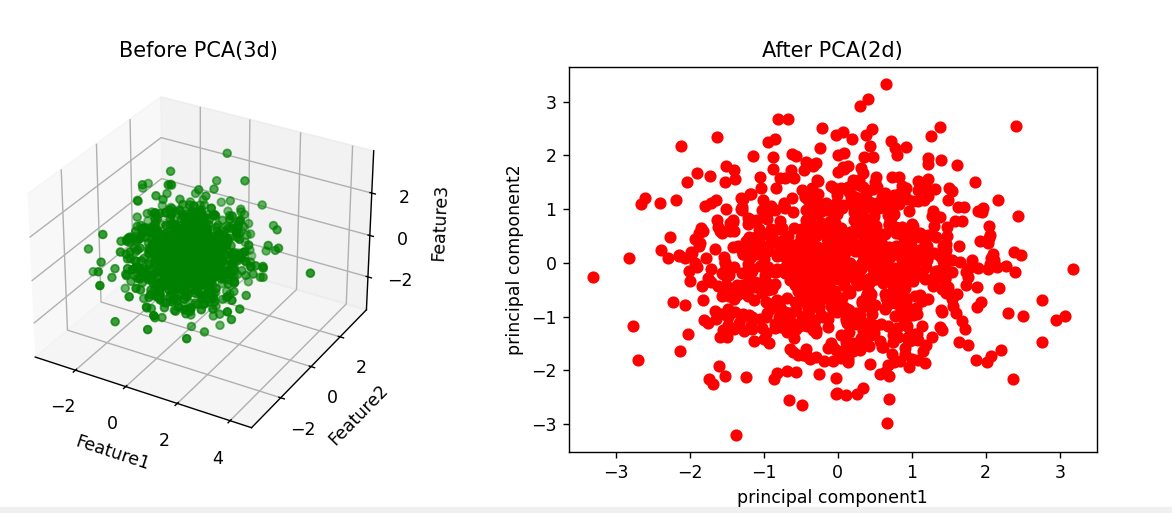
# 转换前的3维数据可视化
fig=plt.figure(figsize=(12,4)) # 创建一个新的图形窗口，尺寸12*4
'''
fig.add_subplot():在图形对象fig添加子图
121:表示子图布局为1行2列的第1个位置
projection=‘3d’指定子图为3d坐标系(默认为2d)
'''
ax1=fig.add_subplot(121,projection='3d')
ax1.scatter(X[:,0],X[:,1],X[:,2],c='g')# :表示所有行
ax1.set_title('Before PCA(3d)')
ax1.set_xlabel('Feature1')
ax1.set_ylabel("Feature2")
ax1.set_zlabel('Feature3')
# 转化后的2维数据可视化
ax2=fig.add_subplot(122)
ax2.scatter(X_pca[:,0],X_pca[:,1],c='r')
ax2.set_title('After PCA(2d)')
ax2.set_xlabel('principal component1')
ax2.set_ylabel("principal component2")
plt.show() # plt.show()是阻碍进程运行展示，若fig.show()会一闪而逝# 手动构建线性相关的三组特征数据
n=1000
# 定义两个主成分方向向量(就是一维ndarray数组)，若矩阵是二维ndarray数组
pca1=np.random.normal(0,1,n)
pca2=np.random.normal(0,0.2,n)
# 再加一个噪声
noise=np.random.normal(0,0.05,n)
# 构建3个特征的输入数据X
X=np.vstack((pca1+pca2,pca1-pca2,2*pca1+3*pca2+noise)).T# vstack将ndarray数组按行叠加
Pca=PCA(n_components=2)
X_Pca=Pca.fit_transform(X) # X是ndarray数组
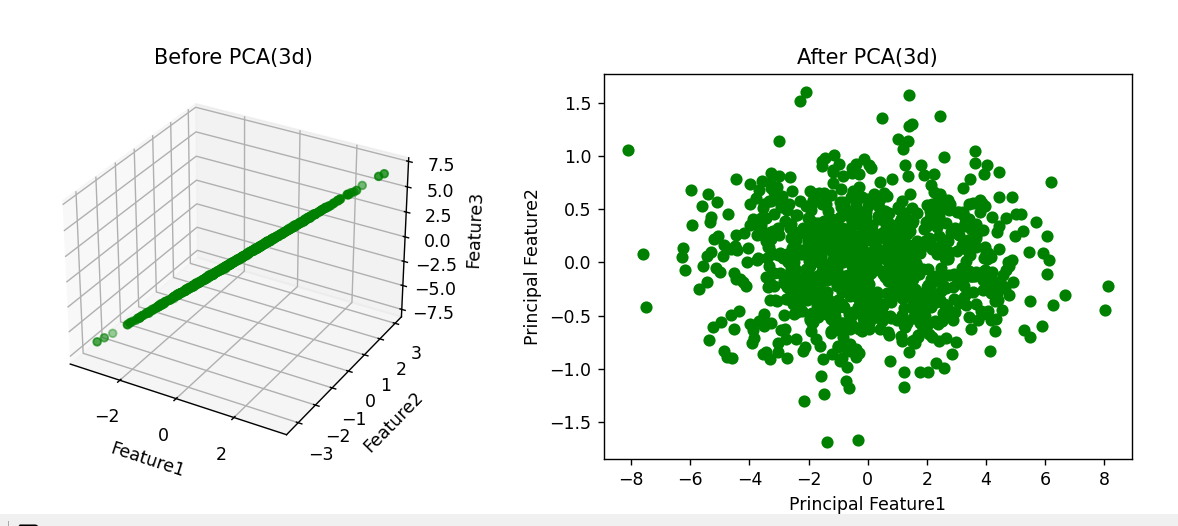
# 转换前的3维数据可视化
fig=plt.figure(figsize=(12,4))
sx1=fig.add_subplot(121,projection='3d')
sx1.scatter(X[:,0],X[:,1],X[:,2],c='g')
sx1.set_title("Before PCA(3d)")
sx1.set_xlabel("Feature1")
sx1.set_ylabel('Feature2')
sx1.set_zlabel("Feature3")
# 转化后的2维可视图
sx2=fig.add_subplot(122)
sx2.scatter(X_Pca[:,0],X_Pca[:,1],c='g')
sx2.set_title("After PCA(3d)")
sx2.set_xlabel("Principal Feature1")
sx2.set_ylabel('Principal Feature2')
plt.show()

两个show()运行结果：

2.模型评估与算法(模型)选择

损失函数

0-1损失函数

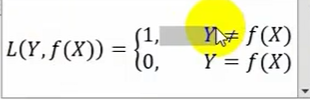
平方损失函数

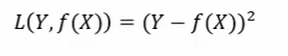
绝对损失函数

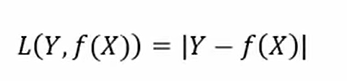
对数似然损失函数

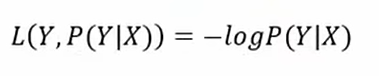
多个概率联合相乘不好算，加个对数就变成相加，然后加个-号最大似然函数就变成求损失函数最小值

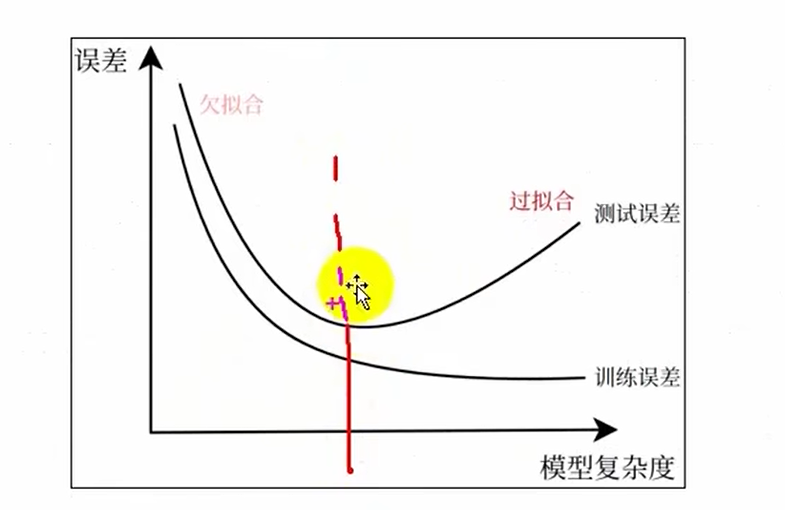
训练(经验)误差与泛化误差

在选择的各种模型下，得出俩误差对比，然后选出最好模型？？？

训练误差最小化不一定是泛化误差最小化，所以两者有矛盾

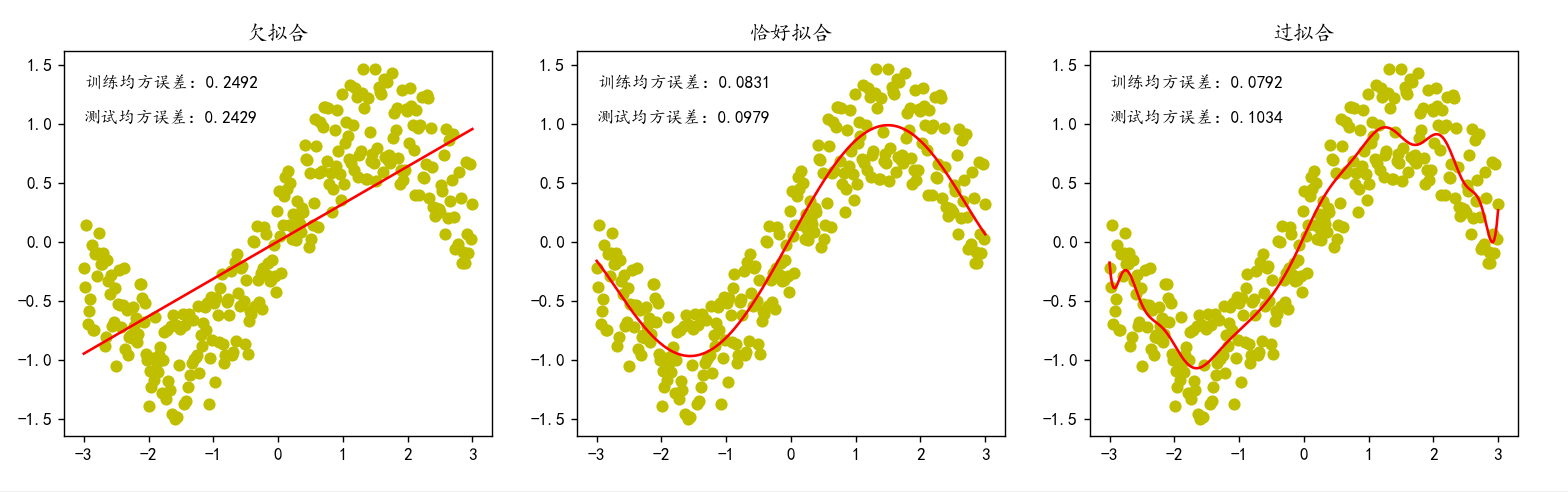
欠拟合和过拟合

基本原理

拟合好坏代表模型泛化能力(考试能力)的强弱

过拟合：模型在训练数据上表现过好，但测试数据上就不行了

欠拟合：模型在训练数据上表现不佳，测试集上也同样表现差

代码案例(整个机器学习过程)

使用多项式在x∈[-3,3]上拟合y=sinx

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plot
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures #构建多项式特征(特征工程)
from sklearn.model_selection import train_test_split #划分训练集和验证(测试)集，在模型评估与选择中是划分训练集和验证集
from sklearn.metrics import mean_squared_error # metrics衡量指标--引入均方误差损失函数plt.rcParams['font.sans-serif']=['kaiTi'] # 字典rcParams,可以用来改plt中的汉字问题
plt.rcParams['axes.unicode_minus']=False #字典rcParams,可以将整个false,默认用ascll码显示
'''
1.生成数据(预处理数据)
2.划分训练集和测试集
3.0特征工程
3.定义模型(线性回归模型)
4.训练模型
5.预测结果，计算误差
'''
# 1.生成数据
X=np.linspace(-3,3,300).T # 随机生成300个(-3,3)数据的ndarray数组,也可以用np.random.randint(-3,3,300)
print(X.shape) # (300,)---生成300个数据的一维数组
'''
要将一维数组转化成300*1的二维数组
'''
X=X.reshape(300,1)
Y=np.sin(X)+np.random.uniform(-0.5,0.5,300).reshape(300,1)
# 画出散点图（3个子图）
fig,ax=plt.subplots(1,3,figsize=(15,4)) #返回一个视窗fig和一个子图1*3的数组ax
ax[0].scatter(X,Y,c='y')
ax[1].scatter(X,Y,c='y')
ax[2].scatter(X,Y,c='y')
#plt.show()
# 2.划分训练集和测试集
(trainX,testX,trainY,testY)=train_test_split(X,Y,test_size=0.2,random_state=42)
# 3.定义模型（线性回归模型）
model=LinearRegression()

# 一。欠拟合（直线）
x_train1=trainX
x_test1=testX
# 4.训练模型
model.fit(trainX,trainY) # or model.fit(X_trainX,trainY)
# 打印查看模型参数
print(model.coef_) #斜率k
print(model.intercept_) #截距
# 5.预测结果，计算均方误差
y_pred1=model.predict(testX) #根据上面训练的模型得出测试集的预测值，
test_loss1=mean_squared_error(testY,y_pred1)
train_loss1=mean_squared_error(trainY,model.predict(trainX))
# 画出拟合曲线,并写出训练误差和测试误差
ax[0].plot(X,model.predict(X),'r')
ax[0].set_title('欠拟合')
ax[0].text(-3,1.3,f"训练均方误差：{train_loss1:.4f}")
ax[0].text(-3,1,f"测试均方误差：{test_loss1:.4f}")
plt.show()

三.过拟合（20次多项式）
poly20=PolynomialFeatures(degree=20)
x_train3=poly20.fit_transform(trainX)
x_test3=poly20.fit_transform(testX)
# 4.训练模型
model.fit(x_train3,trainY)
# 5.得出预测结果用来计算均方误差
train_loss3=mean_squared_error(trainY,model.predict(x_train3))
test_loss3=mean_squared_error(testY,model.predict(x_test3))
# 画出拟合曲线
ax[2].plot(X,model.predict(poly20.fit_transform(X)),c='r')
ax[2].text(-3,1.3,f"训练均方误差：{train_loss3:.4f}")
ax[2].text(-3,1,f"测试均方误差：{test_loss3:.4f}")
plt.show()

plt.rcParams['font.sans-serif']=['kaiTi'] # 字典rcParams,可以用来改plt中的汉字问题

plt.rcParams['axes.unicode_minus']=False #字典rcParams,可以将整个false,默认用ascll码显示，就显示负号了

model.predict()里是已经处理好的特征

plot()中的x与y，是原数据x对应的预测值y，但y也是通过处理好的x来预测的

正则化

其中k是xi前参数的个数(即特征的个数)，模型越复杂k就越大，后面的那项就越大，Loss就上升了

正则化项就是xi前的参数

入是正则化系数，是超参数要手动调节

a.L1正则化(Lasso回归，主要用于特征选择中的嵌入法)

当部分权重趋近0甚至变为0(xi前的参数)，则会触发特则选择，模型自动丢弃一些不重要特征

b.L2正则化(Ridge回归，岭回归)

c.ElasticNet正则化(弹性网络回归)

正则化案例

以多项式在x∈[-3,3]上拟合y=sinx为例,分别不使用正则化,使用L1正则化,使用L2正则化拟合

import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression,Lasso,Ridge #线性回归模型，Lasso回归，岭回归
from sklearn.preprocessing import PolynomialFeatures #构建多项式特征(特征工程)
from sklearn.model_selection import train_test_split #划分训练集和验证(测试)集，在模型评估与选择中是划分训练集和验证集
from sklearn.metrics import mean_squared_error # metrics衡量指标--引入均方误差损失函数
plt.rcParams['font.sans-serif']=['kaiTi'] # 字典rcParams,可以用来改plt中的汉字问题
plt.rcParams['axes.unicode_minus']=False #字典rcParams,可以将整个false,默认用ascll码显示
'''
1.生成数据
2.划分训练集和测试集
(3.0特征工程)
3.定义模型(线性回归模型)
4.训练模型
5.预测结果，计算误差
'''
# 1.生成数据
X=np.linspace(-3,3,300).T # 随机生成300个(-3,3)数据的ndarray数组,也可以用np.random.randint(-3,3,300)'''
要将一维数组转化成300*1的二维数组
'''
X=X.reshape(300,1)
Y=np.sin(X)+np.random.uniform(-0.5,0.5,300).reshape(300,1)
# 画出散点图（2*3个子图）
fig,ax=plt.subplots(2,3,figsize=(15,8)) #返回一个视窗fig和一个子图2*3的数组ax
ax[0,0].scatter(X,Y,c='y')
ax[0,1].scatter(X,Y,c='y')
ax[0,2].scatter(X,Y,c='y')
# 2.划分训练集和测试集
(trainX,testX,trainY,testY)=train_test_split(X,Y,test_size=0.2,random_state=42)
# 过拟合（20次多项式）
poly20=PolynomialFeatures(degree=20)
x_train=poly20.fit_transform(trainX)
x_test=poly20.fit_transform(testX)

# 3.1定义模型（不进行正则化的linearRegression回归）
model1=LinearRegression()
# 4.训练模型
model1.fit(x_train,trainY)
# 5.得出预测结果用来计算均方误差
test_loss1=mean_squared_error(testY,model1.predict(x_test))
# 画出拟合曲线
ax[0,0].plot(X,model1.predict(poly20.fit_transform(X)),c='r')
ax[0,0].set_title('过拟合')
ax[0,0].text(-3,1,f"测试均方误差：{test_loss1:.4f}")
# 画出所有系数的直方图
'''
ax[1,0]操作第二行第一列子图
bar()画直方图
np.arange(21)生成的0~21数字作为x轴
model.coef_.reshape(21)将xi前的所有参数转化成一维ndarray数组作为y轴
'''
ax[1,0].bar(np.arange(21),model1.coef_.reshape(21)) # 21 or -1
print(type(ax)) # ndarray
# plt.show()

# 3.2定义模型（L1正则化的Lasso回归）--特征选择的嵌入法
model2=Lasso(alpha=0.01) # alpha是正则化系数
# 4.训练模型
model2.fit(x_train,trainY)
# 5.得出预测结果用来计算均方误差
test_loss2=mean_squared_error(testY,model2.predict(x_test))
# 画出拟合曲线
ax[0,1].plot(X,model2.predict(poly20.fit_transform(X)),c='r')
ax[0,1].set_title('过拟合')
ax[0,1].text(-3,1,f"测试均方误差：{test_loss2:.4f}")
# 画出所有系数的直方图
ax[1,1].bar(np.arange(21),model2.coef_.reshape(-1)) # 21 or -1
print(type(ax)) # ndarray
#plt.show()

# 3.3定义模型（L2正则化的岭回归）
model3=Ridge(alpha=1) # alpha是正则化系数
# 4.训练模型
model3.fit(x_train,trainY)
# 5.得出预测结果用来计算均方误差
test_loss3=mean_squared_error(testY,model3.predict(x_test))
# 画出拟合曲线
ax[0,2].plot(X,model3.predict(poly20.fit_transform(X)),c='r')
ax[0,2].set_title('过拟合')
ax[0,2].text(-3,1,f"测试均方误差：{test_loss3:.4f}")
# 画出所有系数的直方图
ax[1,2].bar(np.arange(21),model3.coef_.reshape(-1)) # 21 or -1
print(type(ax)) # ndarray
plt.show()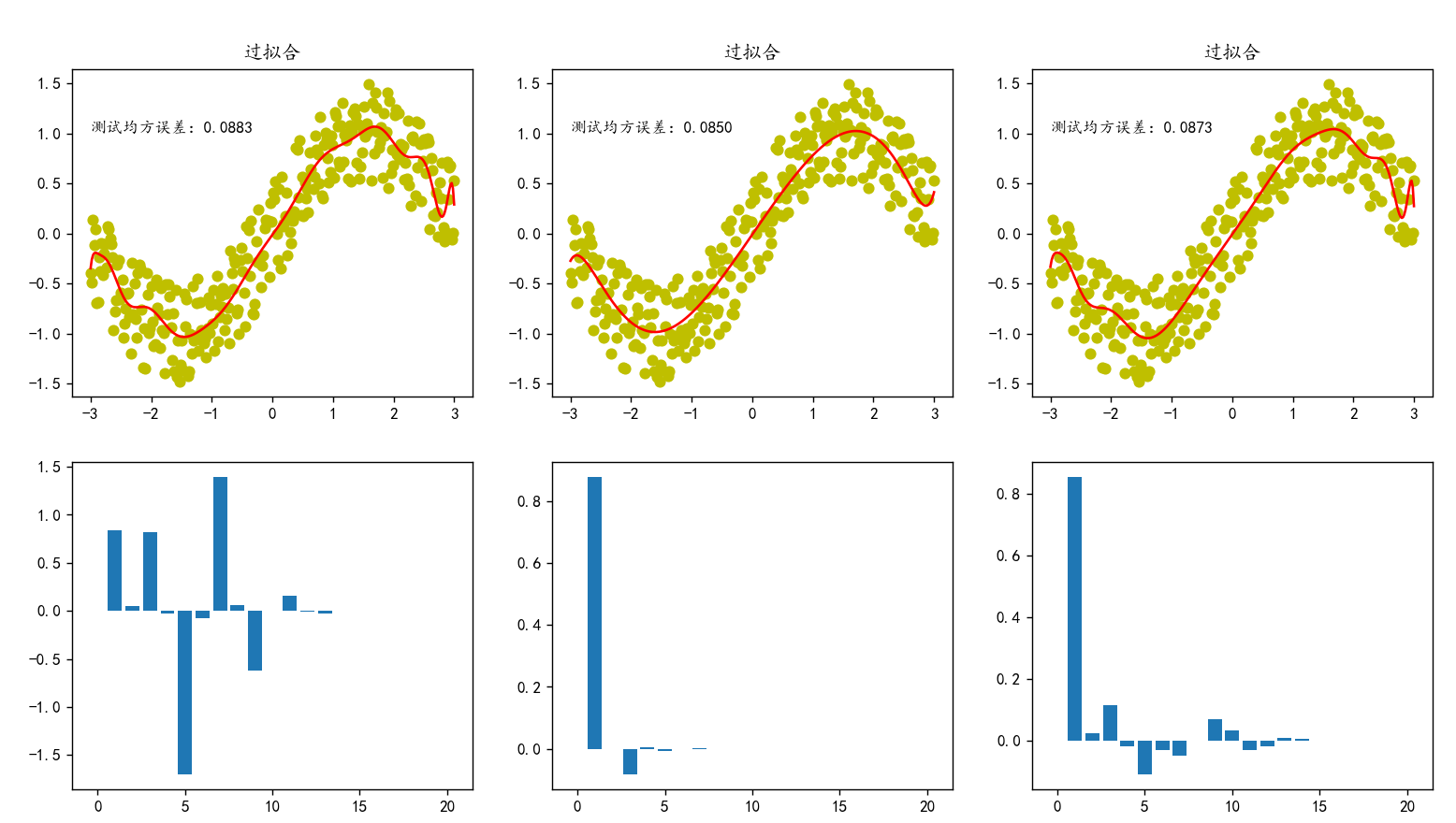

ax[1,1]用来操作多子图布局下的ndarrays数组第二行的第二列子图

交叉验证(选正则化的超参数)

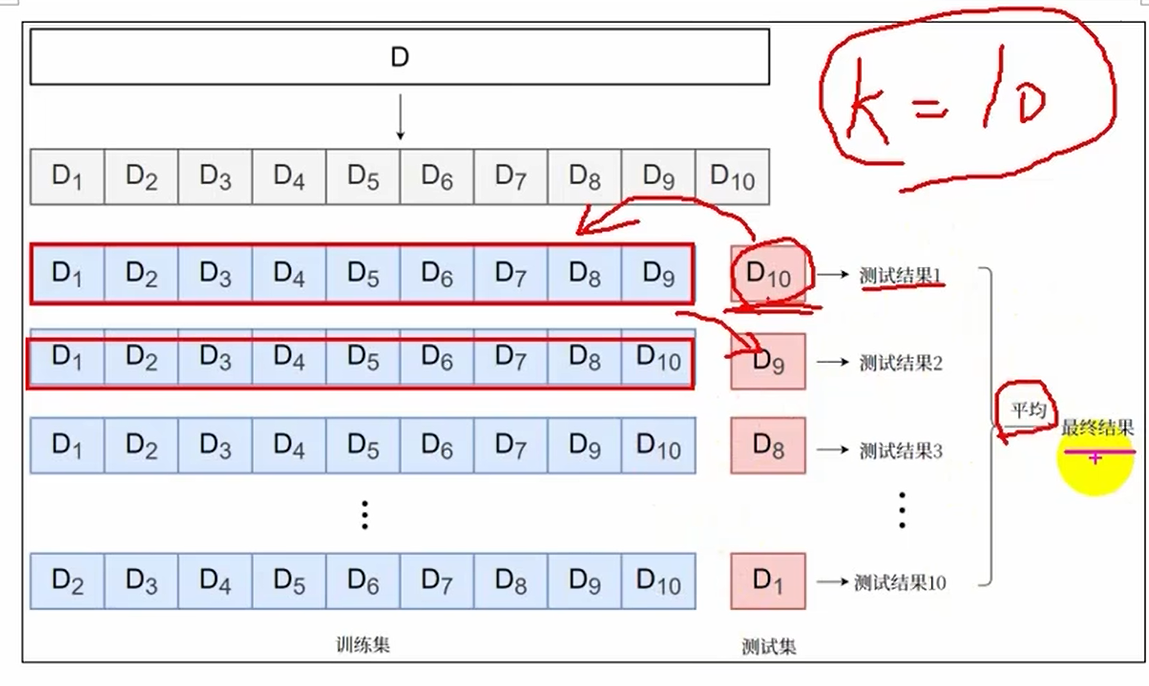
原始数据集‌通常按比例划分为三部分：训练集（60-80%）、验证集（10-20%）、测试集（10-20%） 

3.模型求解算法

解析法

限制条件很多，必须loss函数可以求导且能求出结果。像L1正则化Lasso回归有绝对值就不可以用

梯度下降法

分类

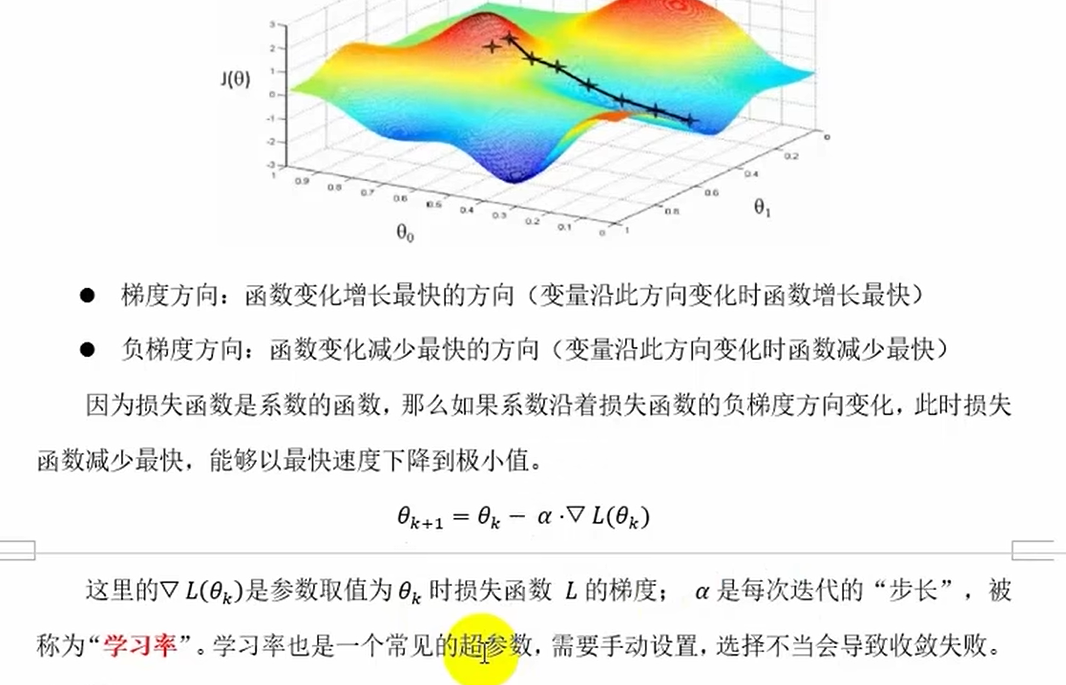
梯度下降计算步骤

代码案例1

求f(x)=x^2的最小值点，x的初始值为1

import numpy as np
import matplotlib.pyplot as plt
# 定义目标函数
def f(x):return x**2
# 定义梯度函数（导函数）
def gradient(x):return 2*x
# 用列表保存点的变化轨迹
x_list=[]
y_list=[]
# 定义超参数和x的初始值
alpha=0.1
x=1
# 重复迭代100次
for i in range(100):y=f(x)# 记录当前点的坐标x_list.append(x)y_list.append(y)#print(f"x={x},y={y}")# 计算梯度grad=gradient(x)# 根据公式更新参数x=x-alpha*grad
# 画图
x=np.arange(-1,1,0.01 )
plt.plot(x,f(x),c='b')
'''
plot()中的x和y支持多种数据结构，包括列表，ndarray,dataframe等
'''
plt.scatter(x_list,y_list,c='g')
plt.show()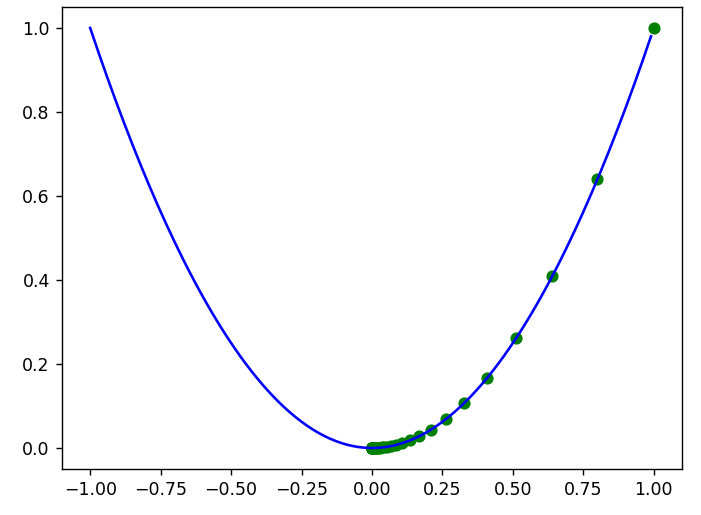

代码案例2

import numpy as np
import matplotlib.pyplot as plt
# 定义目标函数
def J(x):return (x**2-2)**2 # 预测值-真实值
# 定义梯度函数
def gradient(x):return 4*x**3-8*x
# 存储点的变化轨迹，方便观察
x_list=[]
y_list=[]
# 设置超参数和x初始值
alpha=0.1
x=1
# 重复迭代直至梯度＞某个设定好的值循环，否则停止
while np.abs(grad:=gradient(x))>1e-10:y=J(x)x_list.append(x)y_list.append(y)x=x-alpha*grad
# 画出图像
x=np.arange(0.8,1.6,0.01)
plt.plot(x,J(x),c='r')
plt.plot(x_list,y_list,c='b')
plt.scatter(x_list,y_list,c='g')
plt.show()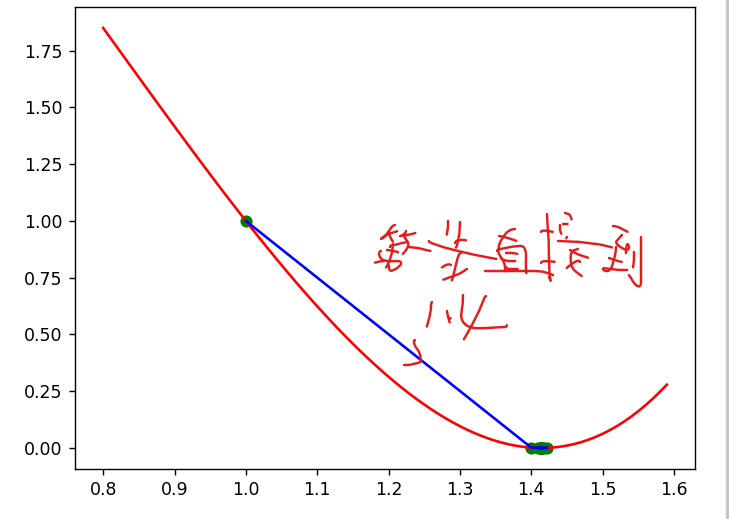

学习率太大结果不能收敛，太小则更新代价太大

梯度下降法的应用

a.L1正则化(Lasso回归)

b.L2正则化(岭回归)

牛顿法和拟牛顿法

4.模型评价指标(性能度量)

注意：模型评价metrics用的是训练集，而超参数选择才用验证集

回归模型评价指标

分类模型评价指标

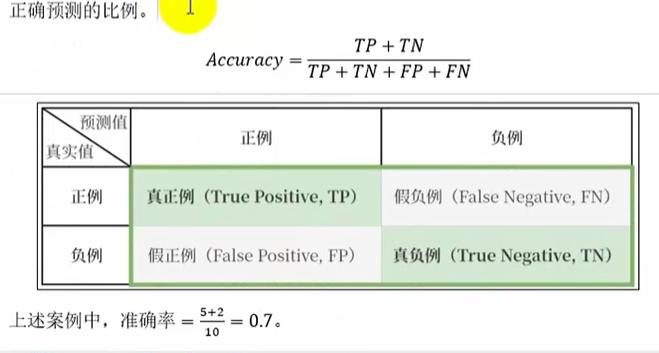
混淆矩阵(评价指标的工具)

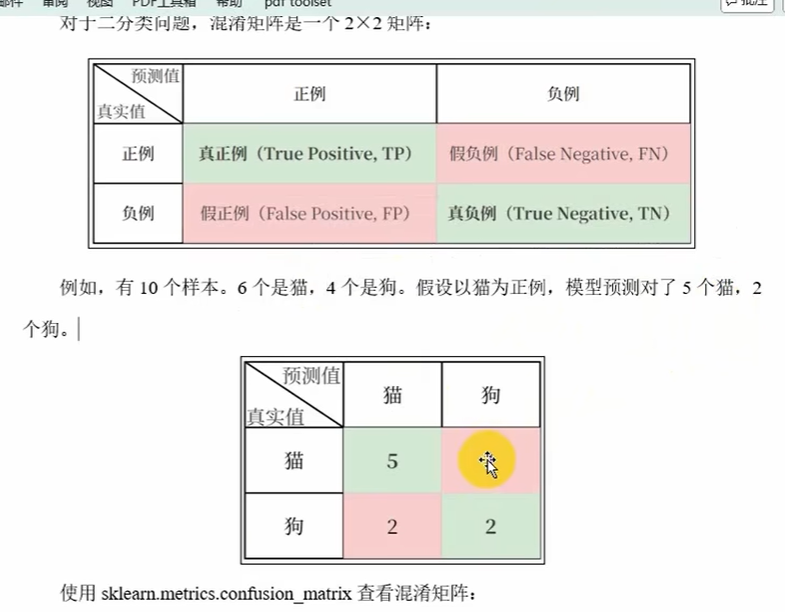
import pandas as pd
from sklearn.metrics import confusion_matrix # 混淆矩阵
import seaborn as sns # 海生热力图
import matplotlib.pyplot as plt
# 定义类别标签
# 假装已经通过机器学习过程得到预测值
labels=['猫','狗']
y_true=['猫','猫','猫','猫','猫','猫','狗','狗','狗','狗']
y_pred=['猫','猫','狗','猫','猫','猫','猫','猫','狗','狗']
# 得到混淆矩阵
matrix=confusion_matrix(y_true,y_true,labels=labels) #ndarray
print(matrix,type(matrix))
print(pd.DataFrame(matrix,columns=labels,index=['猫1','狗1'])) # column列 index行，pd和np可以相互转化
'''
画热力图，
annot=True:显示数据
fmat='d':数据格式为整数
cmap='Greens':颜色格式为绿色
'''
sns.heatmap(matrix,annot=True,fmt='d',cmap='Greens')
plt.show()

运行结果：

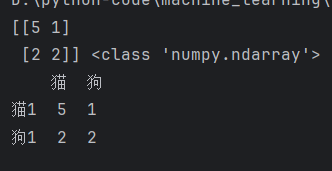
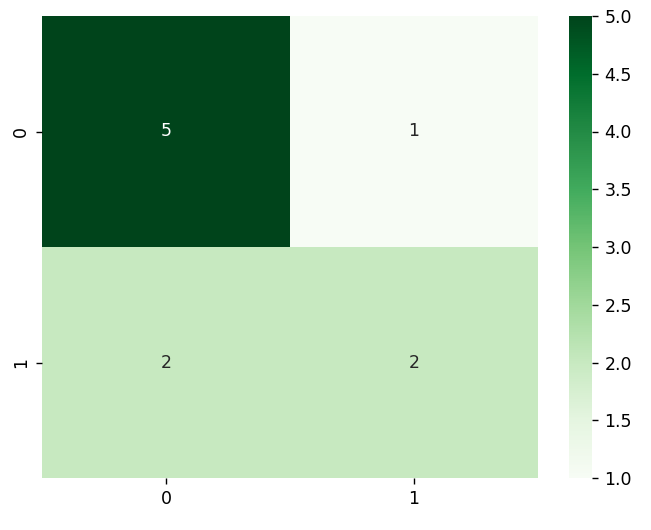
准确率

精确率

召回率

F1