多视图几何--立体匹配--Gipuma

原文：《Massively Parallel Multiview Stereopsis by Surface Normal Diffusion》
参考：
https://github.com/kysucix/gipuma
https://blog.csdn.net/qq_26876733/article/details/102820388
https://blog.csdn.net/fangjin_kl/article/details/76072755

摘要

主要贡献：

1、对patchmatchstereo进行改进，使其可以在GPU并行化，计算时间与图像大小成线性关系，与并行线程数成反比

2、对patchmatch进行多视图聚合，可以生成更精确的深度图

1引言

贡献：

提出了Gipuma——一种简单而强大的多视图Patchmatch立体匹配变体，其采用了一种新的、高度并行的传播方案。

我们的第一个贡献在于提升计算效率：标准的Patchmatch本质上是顺序执行的，因为它以对角线方式在图像中逐像素传播信息。虽然通过将传播方向与图像轴对齐并并行处理行/列[1, 2, 17, 40]可以实现一定程度的并行化，但这些方法仍未能充分利用当前硬件的全部潜力。为此，我们提出了一种新的类扩散方案，该方案基于红黑（棋盘格）模式，能够并行处理图像中一半的像素。实践证明，这种尤其适合现代众核GPU的、可以说更为局部的传播方案，其效果与标准Patchmatch程序相当，但速度却快得多。

第二个贡献旨在提高准确性与鲁棒性：我们将PatchMatch立体匹配从双视图匹配扩展至多视图匹配，以更好地利用多视图数据集中的冗余信息。Patchmatch立体匹配方法本身也会在视差空间中为每个像素恢复一个法向量。我们扩展的出发点是观察到，同样可以在欧几里得3D场景空间中定义这些法向量。在这种情况下，它们能立即定义每个表面点处的局部切平面，从而定义出观察该表面的任意两幅图像之间的关联单应性变换（亦即一对倾斜的支持窗口）。表面法向量的显式估计使得在检查不同视图间的光度一致性时，可以利用平面诱导的单应性变换。这避免了极线校正，并允许在通用配置下聚合多幅图像的证据。

所描述的多视图设置仍然需要一幅参考图像来确定表面的参数化。因此，我们首先依次将每幅图像作为参考图像计算深度，然后将结果融合成一个一致的3D重建模型。然而，我们更倾向于在光度一致性层面谨慎地利用多视图信息，然后使用一个相对基础的融合方案将它们合并成一个一致的3D点云。这与其他一些方法形成对比，那些方法从计算高效但噪声较多的深度图出发，并采用复杂的融合算法进行合并，这些算法（至少是隐含地）必须解决表面拟合这一额外问题[21, 28, 39]。

2patchmatchstereo回顾

Patchmatch立体匹配算法的核心是一种迭代式随机化算法，其目标是为每个像素$p$在视差空间中找到一个平面${\pi }_p$，使得该像素局部邻域内的匹配代价$m$最小化。像素$p$处的代价通过对像素$p$周围的自适应权重窗口$W_p$内作不相似性度量$\rho$累加得到。设$q$为参考图像中落在该窗口内的像素，${\pi }_p$为一个将参考图像中每个像素$q$与另一幅图像中对应位置$q_{{\pi }_p}^{\prime }$相应的平面，则匹配代价为：

$$m(p,{\pi }_p)=\sum _{q\in W_p}w(p,q)\rho (q,q_{{\pi }_p}^{\prime }).\text{\hspace{1em}(1)}$$

权重函数

权重函数 $w(p,q)=e^{-\frac{||I_p-I_q||}{\gamma }}$ 可视为一种软分割策略，其作用是降低与中心像素差异较大的像素的影响。在所有实验中，我们固定设置$\gamma =10$。

不相似性度量

不相似性度量$\rho$由绝对颜色差异与梯度幅值差异的加权和构成。更形式化地说，对于颜色分别为$I_q$和$I_{q_{{\pi }_p}^{\prime }}$的像素$q$与$q_{{\pi }_p}^{\prime }$，有：

$$\rho (q,q_{{\pi }_p}^{\prime })=(1-\alpha )\cdot \min (||I_q-I_{q_{{\pi }_p}^{\prime }}||,{\tau }_{col})+\alpha \cdot \min (||\nabla I_q-\nabla I_{q_{{\pi }_p}^{\prime }}||,{\tau }_{grad}),\text{\hspace{1em}(2)}$$

其中：

• $\alpha$ 用于平衡两项的贡献；

• ${\tau }_{col}$ 和 ${\tau }_{grad}$ 为截断阈值（用于增强代价对异常值的鲁棒性）；

• 在所有实验中，我们设置 $\alpha =0.9$ 、 ${\tau }_{col}=10$ 且 ${\tau }_{grad}=2$ 。

空间点$[x,y,disp{]}^{\top }$必须满足平面方程：

$$\begin{gathered} {\tilde{\mathbf{n}}}^{\top }\mathbf{P}=-\tilde{\mathbf{d}} \\ {a}_f=-\frac{n_x}{n_z} \\ {b}_f=-\frac{n_y}{n_z} \\ {c}_f=\frac{n_x{x}_0+n_y{y}_0+n_z{z}_0}{n_z} \\ disp=-\frac{1}{{\tilde{n}}_z}(\tilde{\mathbf{d}}+{\tilde{n}}_{x}x+{\tilde{n}}_{y}y),\text{\hspace{1em}(3)} \end{gathered}$$

其中$a_f,b_f,c_f$视差平面系数，$\tilde{\mathbf{n}}$为法向量，$\tilde{\mathbf{d}}$为到原点的距离。该定义在校正后的配置中产生了支持窗口的仿射畸变[17]。

3红黑传播

3.1表面法线扩散

标准的Patch matching过程是将信息沿对角线传播的，从左上到右下或者相反方向交替进行传播。该算法本质上是顺序的，因为每一个点都依赖于前一个点。通过将传播方向与图像轴对齐和并行[ 1、2、17、40]中的行/列运行等过程可以实现少量的并行化，但这些仍然没有完全利用当前硬件的能力。

相反，我们提出了一种专门针对GPU处理器等多核架构的新的类扩散方案。我们以棋盘格模式将像素划分为"红色"和"黑色"组，并同时依次更新所有的黑色和红色像素。在给定的像素更新中，可能的候选点仅是局部邻域中属于各自的其他(红色/黑色)组的点，见图2a。

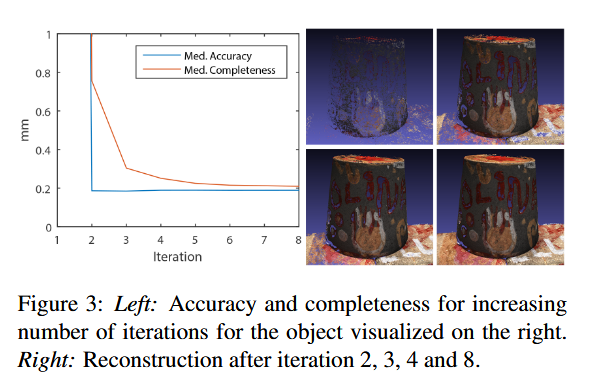
红黑方案是一种用于并行化消息传递型更新过程的标准技巧，例如线性方程求解中的红黑高斯-赛德尔方法。置信传播算法也曾提出采用红黑加速策略[11]。事实上，PatchMatch算法可被解读为连续空间中的一种置信传播形式[4]。与这些红黑方案的应用不同，我们的视野超越了直接相邻单元。如图2b所示，我们的标准模式采用20个局部邻域进行传播。得益于更大的邻域范围，我们仅需较少迭代次数即可收敛到优质解（参见图3）。该设计方案被证明是在单次传播步骤成本与信息远距离扩散所需迭代次数之间的理想平衡。在所有实验中，我们将迭代次数固定为8次。此时深度图已基本收敛，后续变化微乎其微。

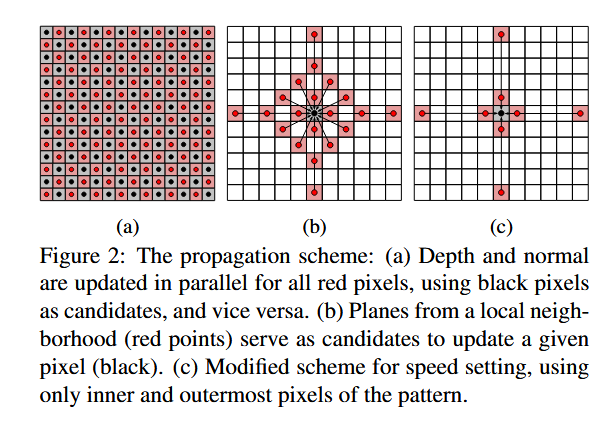
3.2稀疏匹配代价

我们采用了与原始Patch matching文献[ 5 ]中提出的相似的匹配代价。唯一不同的是，我们只考虑灰度度而不考虑颜色差异。当使用RGB时，性能改善很小，在我们看来，并不能证明运行时间增加三倍。（使用灰度单通道，不使用RGB三通道）为了进一步加快计算速度，我们采用了所谓的稀疏Census变换[ 41 ]的思想，在计算匹配代价时只使用窗口中的每一行和每一列，从而得到4倍的增益。在经验上，我们没有观察到这种稀疏代价下匹配精度的任何下降。

3.3应用细节

我们在CUDA中实现了Gipuma，并在最近的桌面计算机游戏显卡上进行了测试。我们的实验使用了Nvidia GTX 980。图像被映射到纹理存储器中，纹理存储器提供硬件加速的双线性插值来调整视图之间的支持窗口。为了限制从GPU内存读取时的延迟，我们广泛使用共享内存，并缓存参考相机的支持窗口。我们在GPLv3许可证下将代码作为开源软件发布。

运行时间：我们的方法的运行时间主要受三个因素的影响：用于匹配的图像数量，图像分辨率和匹配窗口(这在实际中与图像大小大致成正比)的大小。对于分辨率为1600 × 1200的图像，10张图像、窗口大小为25的单幅深度图的时间为50秒。当使用5 . 1节的策略和窗口大小为15时，相同图像数量的运行时间为2.7秒。从10个视图生成分辨率为640 × 480的Middlebury深度图，运行时间为2.5秒。

4多视图拓展

4.1场景空间的参数化

根据定义，视差是针对一对校正图像而言的。与之不同，我们提出在欧几里得场景空间中运用平面patch进行处理。这种方式具有多个优点。首先，它避免了在多视图设置中相当不自然且繁琐的极线校正或显式极线追踪过程。其次，作为附带结果，它能在3D场景空间中生成一个密集的表面法向量场。这可用于改进后续的点云融合（例如，可以过滤那些深度一致但法向不一致的像素），并能直接为表面重建[26]提供所需的法向信息。此外，这种方式使得数据成本能够直接聚合来自多个视图的证据：每个像素的成本是通过参考相机相对于所有其他选定视图的成本来计算的。最后，这一改进带来的额外成本很小：任意两幅图像之间的映射是平面诱导的单应性变换[16]，对应于一次三维矩阵-向量乘法，见图4。

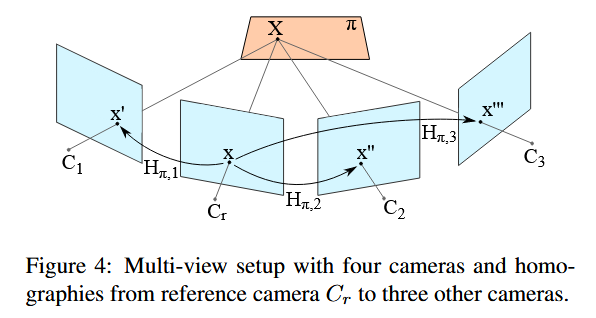
在欧几里得场景空间中，对于三维物体点 $X=[X,Y,Z{]}^T$ ，其满足平面方程 $n^{T}X=-d$ 。找到该物体点等价于求取视线与空间平面的交点。在不失一般性的前提下，可将参考相机置于坐标系原点。通过内参标定矩阵 $K$ ，像素点$x=[x,y{]}^T=[K|0]X$ 处的深度与平面参数的关系可表示为：

$$Z=\frac{-dc}{[x-u,\alpha (y-v),c]\cdot n},K=\left[\begin{array}{ccc}c& 0& u\\ 0& c/\alpha & v\\ 0& 0& 1\end{array}\right].\text{\hspace{1em}(4)}$$

其中$u,v$ 是以像素为单位的主点坐标， $c,\frac{c}{\alpha }$ 分别表示以像素为单位的相机焦距。

参考相机$K[|0|]$ 中的图像点$x$ 与另一相机$K^{\prime }[R|t]$ 中的对应点$x^{\prime }$ 通过平面诱导的单应性变换建立关联(局部窗口内，同名点对x,x‘都在相同的空间平面上，所以这两个点可以使用单应矩阵进行变换)：

$$H_{\pi }=K^{\prime }(R-\frac{1}{d}t{n}^T)K^{-1},x^{\prime }=H_{\pi }x.\text{\hspace{1em}(5)}$$

公式4的推导：

公式4描述了在欧几里得场景空间中，深度Z与平面参数之间的关系。推导过程基于平面方程和相机投影模型。

• 平面方程为 $n^{T}X=-d$ ，其中 $n$ 是平面的法向量（单位向量）， $d$ 是常数， $X=[X,Y,Z{]}^T$ 是3D场景点。

• 参考相机被放置在坐标原点，其内参矩阵为 $K$ ，像素点 $x=[x,y{]}^T$ 对应于3D点 $X$ 的投影关系为 $\mathbf{x}=KX$ ，其中 $\mathbf{x}=[x,y,1{]}^T$ 是齐次坐标形式。

• 从投影关系解出 $X$ ，有 $X=Z{K}^{-1}\mathbf{x}$ ，其中 $Z$ 是深度值。

• 将 $X$ 代入平面方程：

  $$n^T(Z{K}^{-1}\mathbf{x})=-d$$

  简化得：

  $$Z{n}^T{K}^{-1}\mathbf{x}=-d$$

  因此：

  $$Z=\frac{-d}{n^T{K}^{-1}\mathbf{x}}$$

现在，考虑内参矩阵 $K$ 的具体形式：

$$K=\left[\begin{array}{ccc}c& 0& u\\ 0& c/\alpha & v\\ 0& 0& 1\end{array}\right]$$

其中 $u,v$ 是主点坐标（像素单位），$c$ 和 $c/\alpha$ 是焦距（像素单位）。计算 $K^{-1}$：

$$K^{-1}=\left[\begin{array}{ccc}\frac{1}{c}& 0& -\frac{u}{c}\\ 0& \frac{\alpha }{c}& -\frac{\alpha v}{c}\\ 0& 0& 1\end{array}\right]$$

计算 $K^{-1}\mathbf{x}$:

$$K^{-1}\mathbf{x}=\left[\begin{array}{c}\frac{x-u}{c}\\ \frac{\alpha (y-v)}{c}\\ 1\end{array}\right]$$

然后计算 $n^T{K}^{-1}\mathbf{x}$:

$$n^T{K}^{-1}\mathbf{x}=n_x\frac{x-u}{c}+n_y\frac{\alpha (y-v)}{c}+n_z\cdot 1=\frac{1}{c}\left[n_x(x-u)+n_y\alpha (y-v)+n_{z}c\right]$$

注意，分母中的点积 $[x-u,\alpha (y-v),c]\cdot n$ 正好是 $n_x(x-u)+n_y\alpha (y-v)+n_{z}c$，因此：

$$Z=\frac{-d}{n^T{K}^{-1}\mathbf{x}}=\frac{-d}{\frac{1}{c}\left([x-u,\alpha (y-v),c]\cdot n\right)}=\frac{-dc}{[x-u,\alpha (y-v),c]\cdot n}$$

这就是公式4。推导的关键在于将平面方程与相机投影模型结合，并通过内参矩阵的逆变换得到深度表达式。

对公式5的理解

公式5描述了平面诱导的单应性变换（plane-induced homography）：

• 在局部窗口内，如果两个同名点 $x$ （参考相机中的点）和 $x^{\prime }$ （另一个相机中的点）对应同一个3D空间平面上的点，那么它们之间可以通过一个单应矩阵 $H_{\pi }$ 进行变换。

• 公式5为：

  $$H_{\pi }=K^{\prime }\left(R-\frac{1}{d}t{n}^T\right)K^{-1},x^{\prime }=H_{\pi }x$$

  其中 $K^{\prime }$ 是另一个相机的内参矩阵，$R$ 和 $t$ 是从参考相机到另一个相机的旋转和平移，$n$ 和 $d$ 是平面参数。

• 这个单应矩阵直接编码了平面在两个相机视图之间的几何关系，避免了显式的极线校正，并允许在多个视图之间聚合信息。

• 局部窗口内，同名点对x,x’都在相同的空间平面上，所以这两个点可以使用单应矩阵进行变换"准确捕捉了公式5的本质。这种单应变换是多视图立体匹配中的核心思想，用于高效计算像素间的对应关系。

​初始化。​​

当在场景空间中操作时，必须谨慎以确保 PatchMatch 求解器的随机初始化是正确且无偏的。为了高效地生成在可见半球上均匀分布的随机法线，我们遵循 [29] 的方法：从区间 (–1, 1) 内的均匀分布中选取两个值 $q_1$ 和 $q_2$ ，直到这两个值满足$S=q_1^2+q_2^2<1$ ,然后，通过如下映射

$$\mathbf{n}={\left[\begin{array}{c}1-2S,2q_1\sqrt{1-S},2q_2\sqrt{1-S}\end{array}\right]}^{\top }\text{\hspace{1em}(6)}$$

通过公式 (6)可以得到在球面上均匀分布的单位向量。如果投影

$[u,v,c{]}^{\top }\cdot \mathbf{n}$ 在主光线上为正值，则该向量被取反。

此外，还应考虑到一个众所周知的事实：深度分辨率是各向异性的。即使匹配是在场景空间中参数化的，相似性仍然是在图像空间中测量的。由此可知，在视差范围内，测量精度大致恒定，且与深度成反比（或近似与深度的平方成反比；此处原文 *“inversely proportional to the depth”* 可能根据上下文理解为与深度本身成反比，或更常见的与深度平方成反比，但按字面直译为“与深度成反比”）。因此，建议从可能的视差范围中均匀地抽取样本，并将其转换为深度值（也就是说，提供一个在近场区域更密集采样的深度集，因为这些深度值会产生较大影响；以及在远场区域更稀疏的深度集，因为在远场区域小的变化不会产生可观察的差异）。出于同样的原因，平面细化步骤的搜索间隔应与深度成比例设置。

4.2 多图像成本计算

当使用多视图时，如何最佳地将图像间的两两差异合并为一个统一的代价值便成为一个问题。在我们的实现中，我们仅考虑参考图像与所有其他重叠视图之间的两两相似性，而不考虑非参考图像之间的相似性。

视图选择

对于给定的参考图像，我们首先排除所有那些与参考图像的视角方向差异小于 α_min 或大于 α_max 的视图。这两个阈值基于以下经验观察：基线 < α_min 过小，不利于三角测量并会导致过高的深度不确定性；而基线 > α_max 则会因透视畸变过大而无法可靠地比较外观[37]。α_min 和 α_max 的选择取决于具体的数据集。在大型数据集中，即使应用角度标准后视图数量仍然过多时，如果运行时性能优先于精度，我们建议仅在此筛选范围内随机选取一个子集 S 的视图（参见第5节）。当采用此方法时，我们设定 S = 9。

代价聚合

对于特定的平面 π，我们从 N 次比较中各自获得一个成本值 mi。存在不同的策略将这些成本值融合为一个单一的多视图匹配成本。一种可能的方法是如 Okutomi 和 Kanade [30] 所提出的，对所有 n 个成本值进行累加。然而，如果物体在某些视图中被遮挡，那么即使是正确的平面，这些视图也会返回高成本值，从而使目标函数变得模糊不清。为了稳健地处理这种情况，我们遵循 Kang 等人 [24] 的方法。他们假设对于给定的点，至少应有一半的图像是有效的，因此提议只纳入所有 N 个成本值中最好的 50%。我们对此稍作修改，引入了一个参数 K 来指定需要考虑的单个成本值的数量，以替代固定的 50%：

$$m_{\text{srt}}={\text{sort}}_{\uparrow }(m_1\dots m_N),m_{\text{mv}}=\sum _{i=1}^K{m}_i\text{\hspace{1em}(7)}$$

4.3融合

与其他多视图重建方案类似，我们首先通过将所有$N$个视图依次作为参考视图来计算每个视图的深度图。随后，将$N$个深度图融合成一个统一的点云，以消除错误的深度值，并通过在一致的深度和法向量估计上进行平均来降低噪声。我们的方法遵循这样的理念：首先生成最优的独立深度图，然后以直接的方式将它们合并成完整的点云。

一致性检查

误匹配主要出现在无纹理区域、遮挡区域（包括相机视锥体外的区域）。许多此类情况可以通过检测不同视角下估计的深度是否相互一致来识别。具体方法是：依次将每幅图像声明为参考视图，将其深度图转换为稠密的三维点集，并将这些点重投影到其余$N-1$个视图中，得到每个视图中的二维坐标$p_i$和视差值${\hat{d}}_i$。若${\hat{d}}_i$与对应深度图中存储的视差值$d_i$相差不超过$f$个像素（该阈值取决于重建场景的尺度），则认为该匹配是一致的。我们进一步利用估计的表面法向量，并检查法向量差异不超过$f_{ang}$（实验中设置为$30^{\circ }$）。

如果该点在至少$f_{con}$个其他视图中的深度与参考视图一致，则接受对应像素；否则将其剔除。对所有被接受的点，其三维位置和法向量会在场景空间中直接对所有一致视图进行平均计算，以抑制噪声。

总结

本文主要有两个贡献：

1、将像素分为红黑两组，像素视差参数的更新来源于另外一组近邻像素，以此达到并行patchmatchstereo的效果（缺乏理论证明）。

2、将patchmatchstereo拓展到多视图领域，这里的主要创新点在于：观察patchmatchstereo代价函数公式1，2这里面并不包含视差，而是需要同名点即可。因此不进行极线校正也不通过视差寻找同名点，而是使用单应矩阵计算同名点（公式4，5），求解的参数是空间法线，再由法线参数和视差平面求解视差图（公式3）。文中利用视线角度选择近邻视图，同时改进了多个视图的代价聚合函数，然后为每个图像生成一个深度图，最后利用相机位姿转到同一坐标系中，对同名点视差进行视差和法线一致性检查，生成一个完整的最终的视差图。