当前位置：首页 > news >正文

散点拟合圆：Matlab两种方法实现散点拟合圆

news 2025/10/20 7:19:37

文章目录

- 一、散点拟合圆的数学原理
- 二、Python实现
- 三、MATLAB实现
- - 1. 最小二乘法实现
  - 2. 使用优化函数
- 四、Pratt圆拟合方法原理推导
- - 1. 基本数学模型
  - 2. Pratt方法的代数推导
  - 3. 中心化简化计算
  - 4. Pratt方法实现
  - 5. 验证和测试代码

直接拿来使用：

function [xc, yc, R, a] = circfit(x, y)
% 圆拟合函数
% [XC, YC, R, A] = CIRCFIT(X, Y)
% 结果是圆心 (xc, yc) 和半径 R。A 是描述圆方程的可选输出：
% x^2 + y^2 + a(1)*x + a(2)*y + a(3) = 0
n = length(x);
xx = x .* x;
yy = y .* y;
xy = x .* y;
A = [sum(x) sum(y) n; sum(xy) sum(yy) sum(y); sum(xx) sum(xy) sum(x)];
B = [-sum(xx + yy); -sum(xx .* y + yy .* y); -sum(xx .* x + xy .* y)];
a = A \ B;
xc = -0.5 * a(1);
yc = -0.5 * a(2);
R = sqrt((a(1)^2 + a(2)^2) / 4 - a(3));
theta = 0:0.1:2 * pi;
Circle1 = xc + R * cos(theta);
Circle2 = yc + R * sin(theta);
plot(Circle1, Circle2, 'g', 'linewidth', 1);
axis equal;
end

一、散点拟合圆的数学原理

圆的标准方程为：(x - a)² + (y - b)² = r²，其中(a, b)是圆心坐标，r是半径。

最小二乘法的目标是最小化误差平方和：
S(a, b, r) = Σ[(x_i - a)² + (y_i - b)² - r²]²

通过数学变换，可以将非线性问题转化为线性问题求解：

将圆方程展开：x² + y² - 2ax - 2by + (a² + b² - r²) = 0
令C = a² + b² - r²，则方程变为：x² + y² = 2ax + 2by - C
构造线性方程组，使用最小二乘法求解a, b, C
由a, b, C计算出圆心(a, b)和半径r = √(a² + b² - C)

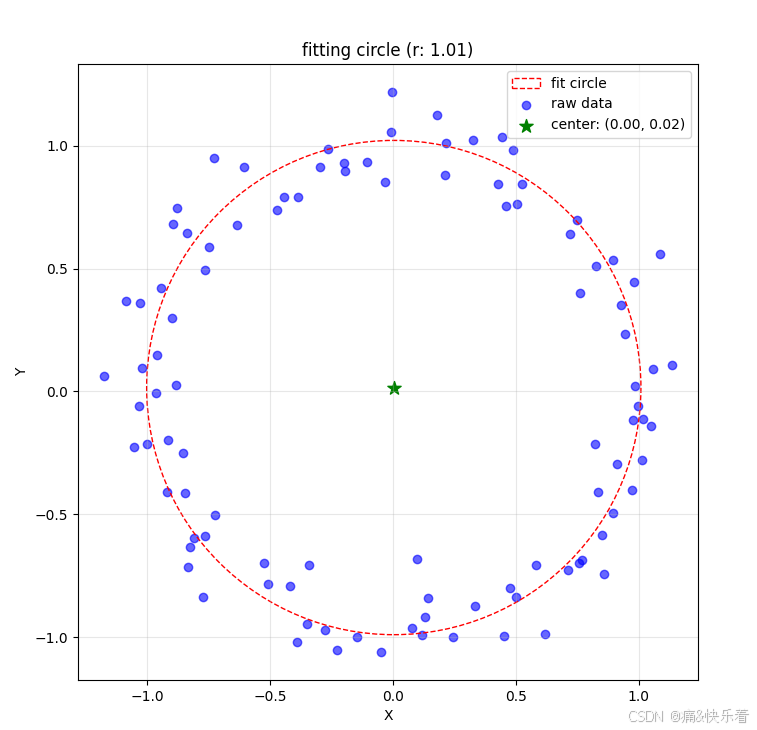
二、Python实现

import numpy as np
import matplotlib.pyplot as pltdef fit_circle_least_squares(x, y):"""使用最小二乘法拟合圆"""# 构造矩阵A和向量CA = np.column_stack([x, y, np.ones_like(x)])C = x**2 + y**2# 解线性方程组B = np.linalg.lstsq(A, C, rcond=None)[0]# 计算圆心和半径a = B[0] / 2b = B[1] / 2r = np.sqrt(B[2] + a**2 + b**2)return a, b, r# 生成测试数据
np.random.seed(42)
theta = np.linspace(0, 2 * np.pi, 100)
x = np.cos(theta) + np.random.normal(0, 0.1, 100)
y = np.sin(theta) + np.random.normal(0, 0.1, 100)# 拟合圆
a, b, r = fit_circle_least_squares(x, y)# 绘制结果
plt.figure(figsize=(8, 6))
plt.scatter(x, y, c='blue', label='Data Points')
theta_fit = np.linspace(0, 2 * np.pi, 100)
plt.plot(a + r * np.cos(theta_fit), b + r * np.sin(theta_fit), 'r-', label='Fitted Circle')
plt.axis('equal')
plt.title('Circle Fitting using Least Squares')
plt.legend()
plt.show()print(f"Fitted circle: center=({a:.4f}, {b:.4f}), radius={r:.4f}")

在这里插入图片描述

三、MATLAB实现

1. 最小二乘法实现

这种方法通过求解线性方程组来拟合圆。代码如下：

function [a, b, r] = fit_circle_least_squares(x, y)% 构造矩阵A和向量CA = [x(:) y(:) ones(size(x(:)))];C = x(:).^2 + y(:).^2;% 解线性方程组B = A \ C;% 计算圆心和半径a = B(1) / 2;b = B(2) / 2;r = sqrt(B(3) + a^2 + b^2);
end% 生成测试数据
rng(42);
theta = linspace(0, 2*pi, 100);
x = cos(theta) + randn(size(theta))*0.1;
y = sin(theta) + randn(size(theta))*0.1;% 拟合圆
[a, b, r] = fit_circle_least_squares(x, y);% 绘制结果
figure;
scatter(x, y, 'b', 'filled');
hold on;
theta_fit = linspace(0, 2*pi, 100);
plot(a + r*cos(theta_fit), b + r*sin(theta_fit), 'r-', 'LineWidth', 2);
axis equal;
title('Circle Fitting using Least Squares');
legend('Data Points', 'Fitted Circle');

2. 使用优化函数

function [a, b, r] = fit_circle_optimization(x, y)% 初始猜测值x_mean = mean(x);y_mean = mean(y);r_mean = sqrt(mean((x - x_mean).^2 + (y - y_mean).^2));% 定义目标函数objFun = @(params) sum((sqrt((x - params(1)).^2 + (y - params(2)).^2) - params(3)).^2);% 优化params = fminsearch(objFun, [x_mean, y_mean, r_mean]);a = params(1);b = params(2);r = params(3);
end% 生成测试数据
rng(42);
theta = linspace(0, 2*pi, 100);
x = cos(theta) + randn(size(theta))*0.1;
y = sin(theta) + randn(size(theta))*0.1;% 拟合圆
[a, b, r] = fit_circle_optimization(x, y);% 绘制结果
figure;
scatter(x, y, 'b', 'filled');
hold on;
theta_fit = linspace(0, 2*pi, 100);
plot(a + r*cos(theta_fit), b + r*sin(theta_fit), 'r-', 'LineWidth', 2);
axis equal;
title('Circle Fitting using Optimization');
legend('Data Points', 'Fitted Circle');

四、Pratt圆拟合方法原理推导

1. 基本数学模型

圆的方程： $x - a)^2 + (y - b)^2 = r^2$

展开得到： $x^2 - 2ax + a^2 + y^2 - 2by + b^2 = r^2$

令 $c = a^2 + b^2 - r^2$ ，得到： $x^2 + y^2 = 2ax + 2by + c$

2. Pratt方法的代数推导

目标函数：最小化代数距离
$min⁡a,b,c∑i=1n[(xi2+yi2)−2axi−2byi−c]2\min_{a,b,c} \sum_{i=1}^n [(x_i^2 + y_i^2) - 2ax_i - 2by_i - c]^2$

构建线性方程组：
令 $z_i = x_i^2 + y_i^2$ ，则问题转化为：
$min⁡a,b,c∑i=1n[zi−2axi−2byi−c]2\min_{a,b,c} \sum_{i=1}^n [z_i - 2ax_i - 2by_i - c]^2$

对 $a, b, c$ 求偏导并令为0：

${∂∂a:∑2xi(zi−2axi−2byi−c)=0∂∂b:∑2yi(zi−2axi−2byi−c)=0∂∂c:∑(zi−2axi−2byi−c)=0\begin{cases} \frac{\partial}{\partial a}: \sum 2x_i(z_i - 2ax_i - 2by_i - c) = 0 \\ \frac{\partial}{\partial b}: \sum 2y_i(z_i - 2ax_i - 2by_i - c) = 0 \\ \frac{\partial}{\partial c}: \sum (z_i - 2ax_i - 2by_i - c) = 0 \end{cases}$

整理得：

${2∑xizi=4a∑xi2+4b∑xiyi+2c∑xi2∑yizi=4a∑xiyi+4b∑yi2+2c∑yi∑zi=2a∑xi+2b∑yi+nc\begin{cases} 2\sum x_i z_i = 4a\sum x_i^2 + 4b\sum x_i y_i + 2c\sum x_i \\ 2\sum y_i z_i = 4a\sum x_i y_i + 4b\sum y_i^2 + 2c\sum y_i \\ \sum z_i = 2a\sum x_i + 2b\sum y_i + nc \end{cases}$

3. 中心化简化计算

为了简化计算，将坐标平移到质心：
$xˉ=1n∑xi,yˉ=1n∑yi\bar{x} = \frac{1}{n}\sum x_i,\quad \bar{y} = \frac{1}{n}\sum y_i$
$ui=xi−xˉ,vi=yi−yˉu_i = x_i - \bar{x},\quad v_i = y_i - \bar{y}$

由于 $∑ui=0\sum u_i = 0$ ， $∑vi=0\sum v_i = 0$ ，方程组大大简化：

${2∑uizi=4a∑ui2+4b∑uivi2∑vizi=4a∑uivi+4b∑vi2∑zi=nc\begin{cases} 2\sum u_i z_i = 4a\sum u_i^2 + 4b\sum u_i v_i \\ 2\sum v_i z_i = 4a\sum u_i v_i + 4b\sum v_i^2 \\ \sum z_i = nc \end{cases}$

其中 $zi=ui2+vi2+2xˉui+2yˉvi+(xˉ2+yˉ2)z_i = u_i^2 + v_i^2 + 2\bar{x}u_i + 2\bar{y}v_i + (\bar{x}^2 + \bar{y}^2)$

4. Pratt方法实现

function [center, radius, residual] = CircleFitByPratt(x, y)
% Pratt圆拟合方法 - 修正版本
% 输入: 每行是一个点[x,y]
% 输出: center - 圆心坐标 [a, b]
%       radius - 半径
%       residual - 残差n = length(x);% 计算质心x_avg = mean(x);y_avg = mean(y);% 中心化坐标u = x - x_avg;v = y - y_avg;% 计算各项和（为什么要求和？）% 这些和是构建线性方程组的基础，来自最小二乘法的正规方程Suu = sum(u.^2);      % ∑u²Svv = sum(v.^2);      % ∑v²  Suv = sum(u.*v);      % ∑uvSuuu = sum(u.^3);     % ∑u³Svvv = sum(v.^3);     % ∑v³Suvv = sum(u.*v.^2);  % ∑uv²Svuu = sum(v.*u.^2);  % ∑vu²% 构建正确的线性方程组% 方程组来源：对代数距离目标函数求偏导得到A = [Suu, Suv; Suv, Svv];B = [(Suuu + Suvv)/2;(Svvv + Svuu)/2];% 求解线性方程组if cond(A) > 1e10% 条件数太大，使用伪逆solution = pinv(A) * B;elsesolution = A \ B;enduc = solution(1);vc = solution(2);% 计算圆心（转换回原坐标系）center = [uc + x_avg, vc + y_avg];a = center(1);b = center(2);% 计算半径% 公式推导：r² = E[(x-a)²+(y-b)²] = E[u²+v²] + (a-x̄)² + (b-ȳ)²alpha = uc^2 + vc^2;radius = sqrt(alpha + (Suu + Svv)/n);% 计算残差if nargout > 2distances = sqrt((x - a).^2 + (y - b).^2);residual = sum((distances - radius).^2);end
end

5. 验证和测试代码

clc;
clear;
close all;% 生成测试数据
rng(42);
n_points = 100;
theta = linspace(0, 2*pi, n_points);
true_radius = 5.0;
true_center = [2.0, 3.0];x = true_center(1) + true_radius * cos(theta) + 0.1 * randn(1, n_points);
y = true_center(2) + true_radius * sin(theta) + 0.1 * randn(1, n_points);% 使用修正的Pratt方法拟合
[center, radius, residual] = CircleFitByPratt(x, y);fprintf('Pratt圆拟合结果:\n');
fprintf('真实圆心: (%.4f, %.4f)\n', true_center);
fprintf('拟合圆心: (%.4f, %.4f)\n', center);
fprintf('圆心误差: %.6f\n', norm(center - true_center));
fprintf('真实半径: %.4f\n', true_radius);
fprintf('拟合半径: %.4f\n', radius);
fprintf('半径误差: %.6f\n', abs(radius - true_radius));
fprintf('残差: %.6f\n', residual);% 可视化
figure;
scatter(x, y, 50, 'filled', 'blue', 'MarkerFaceAlpha', 0.6);
hold on;% 绘制拟合圆
theta_plot = linspace(0, 2*pi, 100);
x_circle = center(1) + radius * cos(theta_plot);
y_circle = center(2) + radius * sin(theta_plot);
plot(x_circle, y_circle, 'r-', 'LineWidth', 2);% 绘制圆心
plot(center(1), center(2), 'ro', 'MarkerSize', 8, 'LineWidth', 2);
plot(true_center(1), true_center(2), 'gx', 'MarkerSize', 10, 'LineWidth', 2);axis equal;
grid on;
xlabel('X');
ylabel('Y');
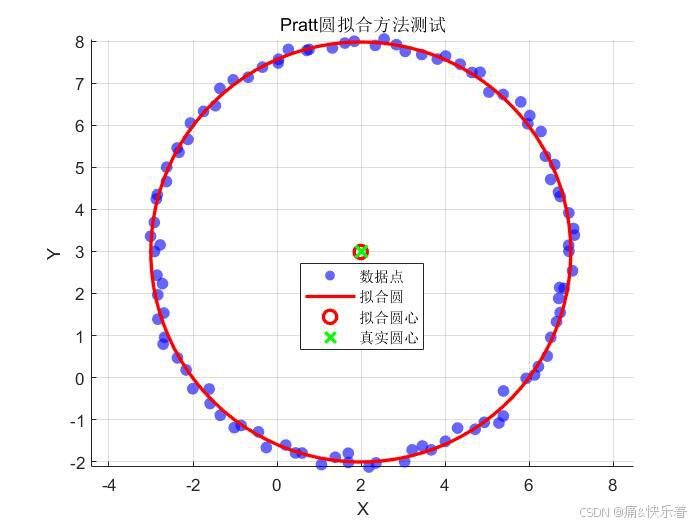
title('Pratt圆拟合方法测试');
legend('数据点', '拟合圆', '拟合圆心', '真实圆心', 'Location', 'best');