当前位置：首页 > news >正文

【机器学习入门】9.1 神经元模型 —— 从生物神经元到人工神经网络基础

news 2025/10/19 18:46:39

对于刚入门机器学习的同学来说，“神经网络” 可能是最具神秘感的模型之一，但它的核心单元 ——“人工神经元”，其实是对生物神经元的简化模仿。今天我们从生物神经元的结构和工作原理出发，拆解人工神经元（感知机）的模型、神经网络的构建逻辑，以及前向传播、反向传播等核心概念，帮你搭建起 “神经元→神经网络” 的完整认知框架，为后续深入学习深度学习打下基础。

一、先理解：生物神经元是如何工作的？

人工神经元的设计灵感完全来源于生物神经元，要搞懂人工模型，首先得清楚生物神经元的结构和信号传递逻辑 —— 这是理解神经网络的 “源头”。

1. 生物神经元的基本结构

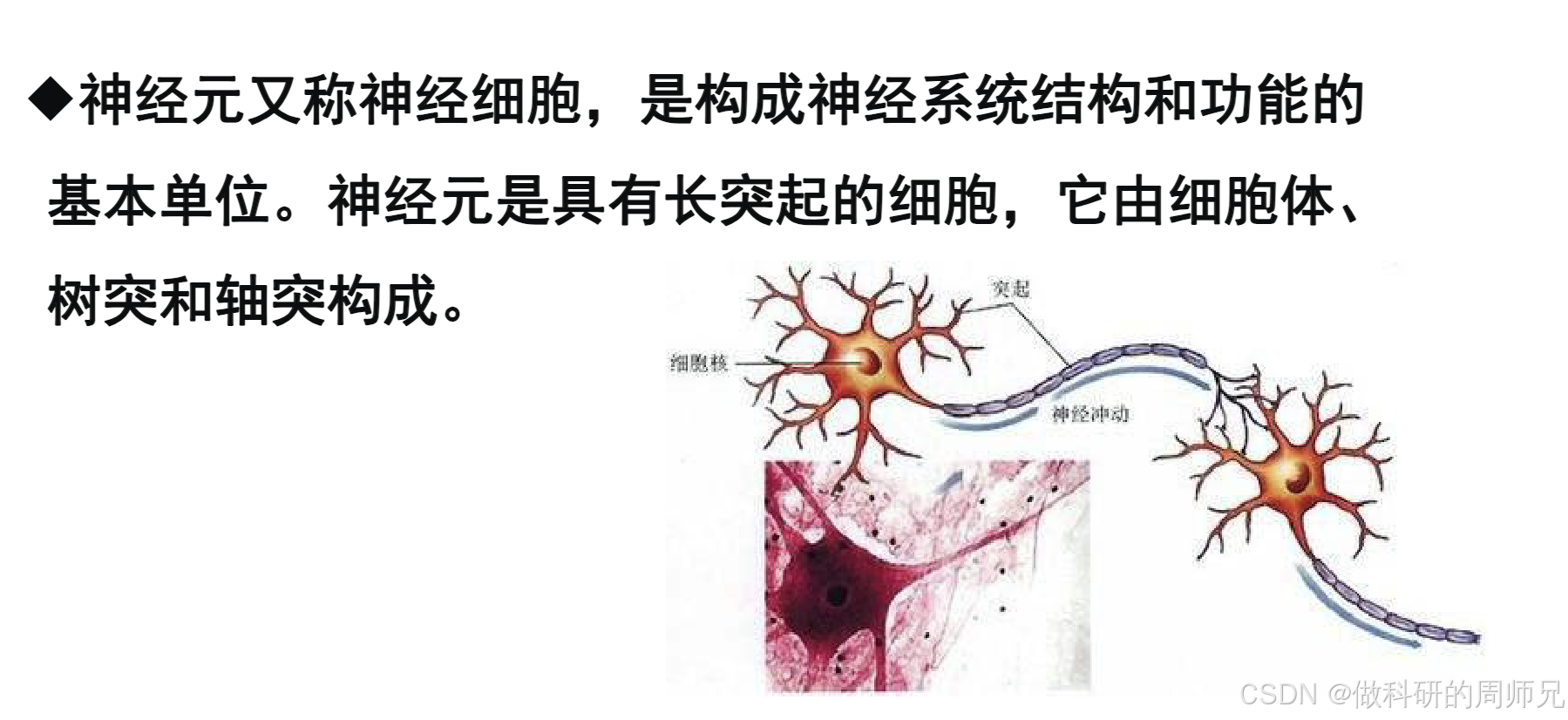
生物神经元（神经细胞）是构成人体神经系统的基本单位，每个神经元都有三个核心部分，分工明确：

树突（输入端）：像 “树枝” 一样的突起，负责接收来自其他神经元的信号（化学信号或电信号）。一个神经元可能有多个树突，就像有多个 “信号接收器”，能同时接收多个神经元的输入。
细胞体（处理中心）：包含细胞核、细胞质等，相当于神经元的 “大脑”。它会把树突接收的多个信号进行整合（比如判断信号的强弱、总和是否达到阈值），决定是否产生 “神经冲动”（即是否传递信号）。
轴突（输出端）：像 “电线” 一样的长突起，负责将细胞体产生的神经冲动传递出去。轴突的末端有 “突触”，能将电信号转化为化学信号，传递给下一个神经元的树突 —— 这样就形成了神经元之间的 “信号通路”。

2. 生物神经元的信号传递逻辑

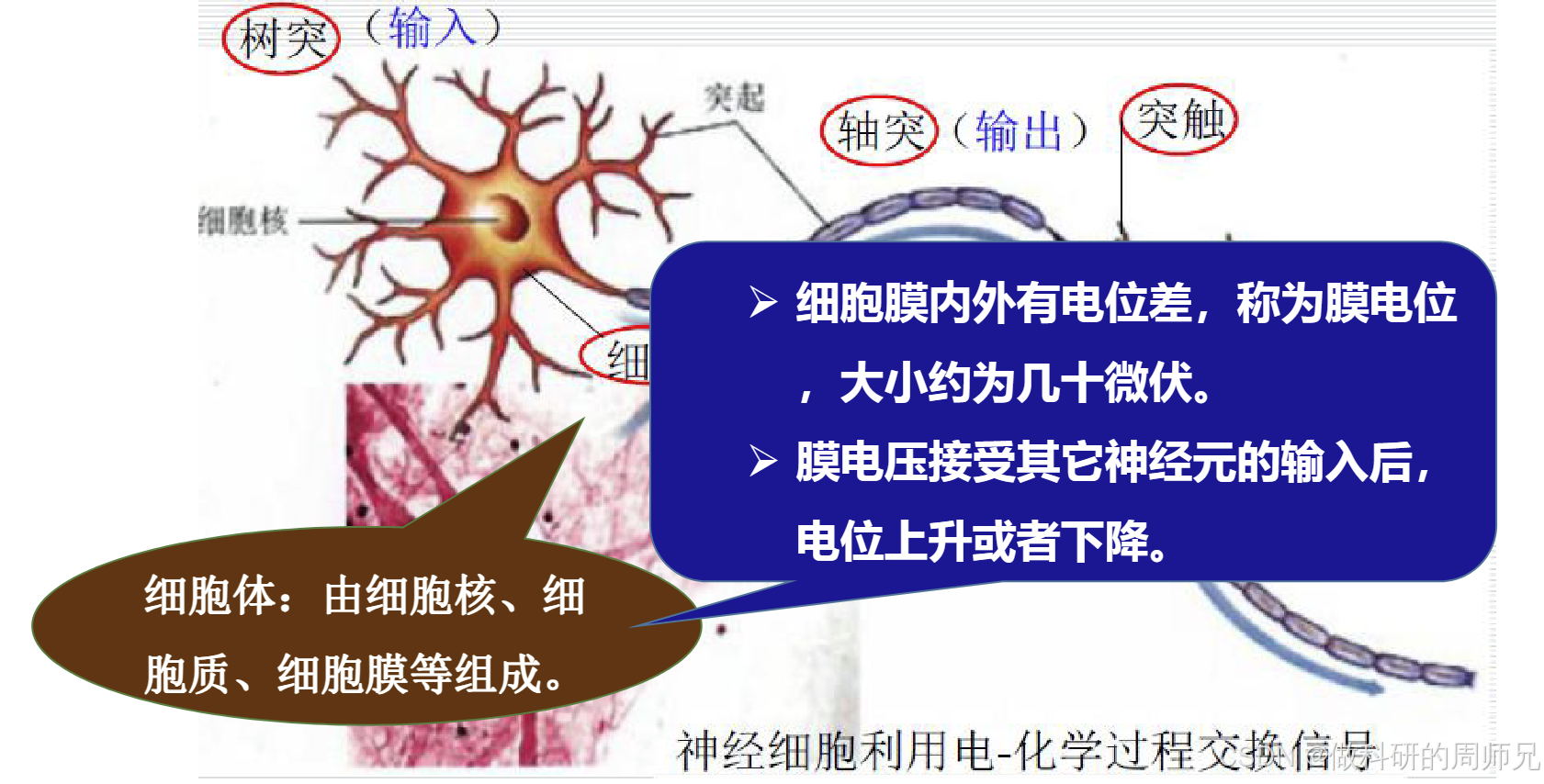
神经元之间的信号传递遵循 “输入→整合→输出” 的简单规则，关键在于 “膜电位” 和 “阈值”：

膜电位：神经元的 “信号储备”：细胞膜内外存在微小的电位差（约几十微伏），称为膜电位。当树突接收其他神经元的信号时，膜电位会上升或下降（接收兴奋信号时上升，接收抑制信号时下降）。
阈值：信号传递的 “开关”：细胞体会持续整合所有树突的信号，当膜电位的总和超过某个 “阈值” 时，神经元会被 “激活”，产生神经冲动；若未达到阈值，则不产生冲动，信号被 “阻断”。
信号传递：电 - 化学转换：激活后的神经冲动会沿着轴突传递，到达突触时转化为化学信号（神经递质），跨越 “突触间隙” 传递给下一个神经元的树突，完成一次信号传递。

简单来说，生物神经元的工作逻辑是：多个输入信号整合→判断是否达到阈值→达到则输出信号，否则不输出—— 这正是人工神经元设计的核心灵感。

二、人工神经元：生物神经元的数学简化模型

人工神经元（也叫 “感知机”，是最简单的人工神经元模型）用数学公式模拟生物神经元的 “输入→整合→输出” 过程，将复杂的生物信号转化为可计算的数值运算。

1. 人工神经元的模型结构

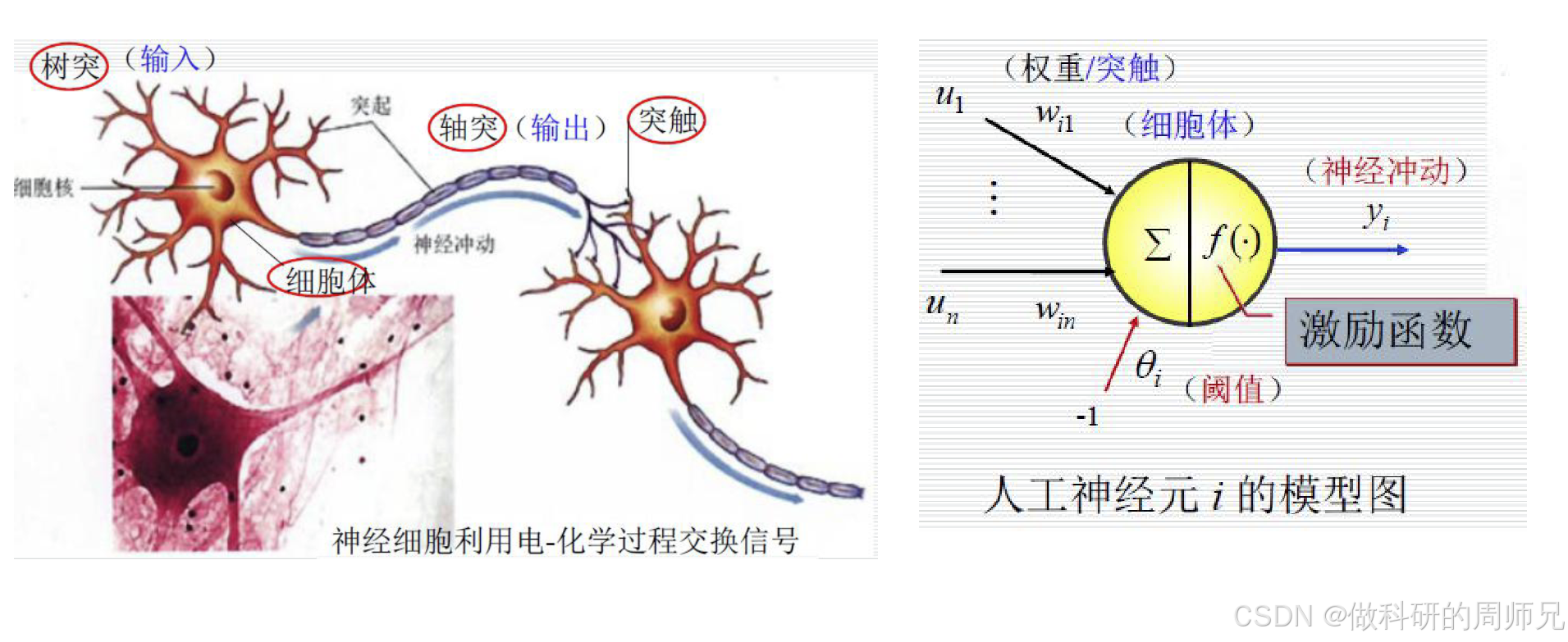
一个标准的人工神经元模型包含 4 个核心组件，对应生物神经元的功能，结构非常直观：

输入（对应树突）：用x₁, x₂, ..., xₙ表示，对应来自其他神经元的输出信号（或原始数据特征，比如 “好瓜” 的色泽、根蒂等特征）。每个输入都有一个 “权重”，用w₁, w₂, ..., wₙ表示。
权重（对应突触）：权重wᵢ代表 “第 i 个输入信号的重要程度”—— 权重越大，该输入对神经元输出的影响越强；权重为正表示 “兴奋信号”（促进输出），为负表示 “抑制信号”（阻碍输出），这对应生物突触传递信号的强弱差异。
细胞体（整合与激活）：分为两步操作：
1. 加权求和：先计算所有输入与对应权重的乘积之和，再减去一个 “阈值”θ（也叫偏置b，通常用-b替代θ，公式更简洁），结果称为 “净输入”z，公式为：z = w₁x₁ + w₂x₂ + ... + wₙxₙ - b （或 z = Σ(wᵢxᵢ) - b）这一步对应生物神经元整合树突信号的过程。
2. 激活函数：将净输入z代入 “激活函数”f(·)，得到神经元的最终输出y，公式为：y = f(z)激活函数的作用是 “引入非线性”—— 如果没有激活函数，无论多少个神经元叠加，最终还是线性模型，无法拟合复杂数据（比如图像、文本）。常见的简单激活函数是 “阶跃函数”：f(z) = 1（若z ≥ 0，神经元激活，输出 1）；f(z) = 0（若z < 0，神经元不激活，输出 0）。
输出（对应轴突）：用y表示，作为当前神经元的结果，传递给下一层的神经元（或作为最终预测结果，比如 “好瓜 = 1，坏瓜 = 0”）。

2. 人工神经元的工作流程（以 “好瓜分类” 为例）

用一个具体案例能更直观理解人工神经元的计算过程：假设用一个人工神经元判断 “是否为好瓜”，输入特征为 “根蒂（x₁）、纹理（x₂）、敲声（x₃）”，具体步骤如下：

输入与权重设定：
- 输入x：根蒂（蜷缩 = 1，稍蜷 = 0.5，硬挺 = 0）、纹理（清晰 = 1，稍糊 = 0.5，模糊 = 0）、敲声（浊响 = 1，沉闷 = 0.5，清脆 = 0）；
- 权重w：根蒂w₁=0.4（关键特征，权重高）、纹理w₂=0.3（重要特征）、敲声w₃=0.2（次要特征）；
- 偏置b=0.5（阈值转化而来）。
加权求和计算净输入：假设某样本的输入为x₁=1（根蒂蜷缩）、x₂=1（纹理清晰）、x₃=1（敲声浊响），则：z = (0.4×1) + (0.3×1) + (0.2×1) - 0.5 = 0.4+0.3+0.2-0.5 = 0.4。
激活函数输出结果：用阶跃函数判断：因z=0.4 ≥ 0，所以y=f(z)=1，最终输出 “好瓜”。

如果另一个样本的输入为x₁=0（根蒂硬挺）、x₂=0（纹理模糊）、x₃=0.5（敲声沉闷），则：z = (0.4×0) + (0.3×0) + (0.2×0.5) - 0.5 = 0+0+0.1-0.5 = -0.4 < 0，输出y=0，判断为 “坏瓜”—— 这完全符合我们对好瓜的判断逻辑。

三、从单个神经元到神经网络：如何搭建多层结构？

单个人工神经元（感知机）只能处理 “线性可分” 的问题（比如用一条直线区分两类样本），但现实中的数据大多是 “非线性” 的（比如用曲线区分好瓜和坏瓜）。要解决非线性问题，就需要将多个人工神经元按 “层” 排列，组成 “神经网络”—— 这就是 “多层感知机” 的基础。

1. 神经网络的基本结构：三层全连接网络

最基础的神经网络是 “输入层→隐藏层→输出层” 的三层结构，且层与层之间的神经元 “全连接”（即上一层的每个神经元都与下一层的所有神经元相连），称为 “全连接网络”：

输入层（Input Layer）：对应原始数据的特征，每个神经元代表一个特征，只负责传递输入，不做任何计算。比如 “好瓜分类” 中，输入层有 3 个神经元，分别对应 “根蒂、纹理、敲声”3 个特征。
隐藏层（Hidden Layer）：位于输入层和输出层之间，是神经网络的 “计算核心”。隐藏层可以有一层或多层（多层时称为 “深度神经网络”），每层包含多个神经元 —— 每个神经元都会接收上一层所有神经元的输出作为输入，进行加权求和 + 激活函数计算，再将结果传递给下一层。比如隐藏层有 2 个神经元，输入层的 3 个神经元都会与这 2 个隐藏神经元相连，形成 3×2=6 个连接（每个连接对应一个权重）。
输出层（Output Layer）：接收隐藏层的输出，进行最终计算，输出模型的预测结果。比如 “好瓜分类” 是二分类任务，输出层可以只有 1 个神经元，输出 1 表示 “好瓜”，0 表示 “坏瓜”；若为多分类任务（如区分 “好瓜、中瓜、坏瓜”），输出层则有 3 个神经元，每个神经元对应一类的预测概率。

2. “全连接” 的含义：层间连接无遗漏

“全连接” 是神经网络中最基础的连接方式，核心特点是 “上一层每个神经元都连接下一层所有神经元”：

假设输入层有n个神经元，隐藏层有m个神经元，则两层之间共有n×m个连接，每个连接都有一个独立的权重（比如输入层 3 个神经元、隐藏层 2 个神经元，就有 6 个权重）；
这种连接方式能让下一层神经元充分整合上一层的所有信息，比如隐藏层神经元能同时利用 “根蒂、纹理、敲声” 三个特征的信息，比单个神经元的判断更全面。

四、神经网络的核心过程：前向传播与反向传播

神经网络的训练和预测依赖两个关键过程：“前向传播”（从输入到输出的预测过程）和 “反向传播”（从输出到输入的参数优化过程）—— 这是神经网络能 “学习” 的核心。

1. 前向传播：从输入到输出的预测流程

前向传播是 “已知参数（权重和偏置），计算预测结果” 的过程，按 “输入层→隐藏层→输出层” 的顺序逐层计算，和单个神经元的工作流程一致，但需要逐层迭代：

输入层传递：输入层神经元直接将原始特征（如x₁=1, x₂=1, x₃=1）传递给隐藏层；
隐藏层计算：隐藏层的每个神经元接收输入层所有神经元的输出，计算加权求和 + 激活函数，得到隐藏层输出（如隐藏层神经元 1 的输出h₁=f(w₁₁x₁ + w₁₂x₂ + w₁₃x₃ - b₁)，神经元 2 的输出h₂=f(w₂₁x₁ + w₂₂x₂ + w₂₃x₃ - b₂)）；
输出层计算：输出层神经元接收隐藏层所有神经元的输出，再次计算加权求和 + 激活函数，得到最终预测结果（如y=f(w₃₁h₁ + w₃₂h₂ - b₃)）。

简单来说，前向传播就是 “逐层代入公式计算”，最终得到预测值 —— 这是模型进行预测时的核心流程（比如用训练好的神经网络判断一个新西瓜是否为好瓜）。

2. 反向传播：从误差到参数的优化流程

反向传播是 “已知预测误差，调整参数（权重和偏置）” 的过程，核心是 “通过误差反向推导，修正权重和偏置，减少误差”—— 这是神经网络 “学习” 的关键，步骤如下：

计算预测误差：用输出层的预测结果y_pred和真实标签y_true计算误差（比如用 “均方误差”Loss=(y_pred - y_true)²），误差越大，说明当前参数越差；
反向计算误差梯度：从输出层开始，反向计算每个参数（权重w、偏置b）对误差的 “梯度”（即参数变化一点点时，误差变化多少）—— 梯度的方向表示 “参数如何调整能减小误差”（比如梯度为正，说明参数需要减小；梯度为负，说明参数需要增大）；
更新参数：根据梯度方向和 “学习率”（控制每次参数调整的幅度，比如 0.01），更新所有参数（公式为w_new = w_old - 学习率×梯度，b_new = b_old - 学习率×梯度）；
迭代优化：重复 “前向传播计算误差→反向传播更新参数” 的过程，直到误差减小到预设值，或迭代次数达到上限 —— 此时神经网络的参数（权重和偏置）已优化完成，能准确预测新样本。

五、神经网络的优化：如何让模型更稳定？

训练神经网络时，很容易出现 “过拟合”（训练集精度高，测试集精度低）或 “训练不稳定”（误差波动大）的问题，需要通过 “正则化” 等方法优化 —— 这是让神经网络实用化的关键。

1. 正则化：防止过拟合的核心手段

正则化的本质是 “限制参数的大小，避免模型过度复杂”，常用的有两种方式：

L2 正则化（权重衰减）：在误差函数中加入 “所有权重的平方和”，公式为Loss = 原始误差 + λ×Σ(wᵢ²)（λ是正则化强度，越大对权重的限制越强）。这样训练时，模型会倾向于选择更小的权重，避免某些权重过大导致过拟合（比如避免过度依赖 “根蒂” 特征，忽略其他特征）；
Dropout（随机失活）：训练过程中，随机 “关闭” 一部分隐藏层神经元（比如每次训练关闭 50% 的神经元），让模型不依赖某个特定神经元的输出，迫使模型学习更通用的特征（比如即使 “根蒂” 特征的神经元被关闭，模型仍能通过 “纹理”“敲声” 判断好瓜）。

2. 其他优化技巧

学习率调整：初始学习率不宜过大（避免参数震荡不收敛），也不宜过小（避免训练过慢），可采用 “学习率衰减”（随着迭代次数增加，逐渐减小学习率）；
批量训练（Batch Training）：每次不使用全部训练样本，而是随机选择一小批样本（比如 32 个或 64 个）进行训练，既能加快训练速度，又能让参数更新更稳定；
激活函数选择：除了简单的阶跃函数，实际中常用 “ReLU 函数”（f(z)=max(0,z)）或 “Sigmoid 函数”（f(z)=1/(1+e⁻ᵢ)），这些函数能更好地处理非线性问题，避免 “梯度消失”（反向传播时梯度越来越小，参数无法更新）。

六、入门总结与神经网络的应用场景

核心逻辑回顾：神经网络是由人工神经元按层组成的模型，人工神经元模仿生物神经元的 “输入→整合→输出” 逻辑，通过前向传播实现预测，通过反向传播优化参数，最终能学习复杂的非线性规律。
关键概念记忆：
- 人工神经元：输入 + 权重 + 加权求和 + 激活函数 + 输出；
- 神经网络结构：输入层（特征）→隐藏层（计算核心）→输出层（预测），层间全连接；
- 核心过程：前向传播（预测）、反向传播（优化参数）；
- 优化方法：正则化（L2、Dropout）、学习率调整、批量训练。
常见应用场景：
- 图像识别：如人脸识别、物体检测（用深度神经网络提取图像特征，判断图像内容）；
- 自然语言处理：如文本分类、情感分析（将文本转化为向量输入神经网络，判断文本情感是正面还是负面）；
- 推荐系统：如商品推荐、视频推荐（用神经网络学习用户行为特征，推荐用户可能喜欢的内容）；
- 回归预测：如房价预测、销量预测（输出层为连续值，预测未来的数值结果）。

对于刚入门的同学，不需要一开始深入反向传播的复杂数学推导（如梯度下降、链式法则），重点是理解 “人工神经元的结构”“神经网络的层间关系” 以及 “前向传播的流程”。后续我们会通过代码实践，带你用 Python 搭建简单的神经网络，直观感受模型的训练和预测过程。

简单神经网络 Python 实践代码模板（好瓜分类数据集适配）

以下代码基于numpy手动实现全连接神经网络，包含网络搭建、前向传播计算、反向传播参数优化（梯度下降），全程贴合 “好瓜分类” 任务，代码注释详细，可直接复制到 CSDN 推文的实践部分，帮助入门学生亲手体验神经网络的 “学习” 过程。

一、环境依赖

确保安装所需 Python 库，未安装则执行以下命令：

pip install numpy pandas matplotlib

二、完整代码实现

1. 导入所需库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.metrics import accuracy_score, classification_report

2. 构建 “好瓜分类” 数据集

基于神经网络输入需求，整理 “好瓜” 核心特征（含分类特征与数值特征），标签设为 “好瓜 = 1，坏瓜 = 0”，确保数据贴合实际分类场景：

# 设置随机种子，保证结果可复现
np.random.seed(42)# 构建好瓜分类数据集（4个分类特征+2个数值特征，共6个输入特征）
good_melon_data = {# 分类特征（文本类型，需编码）"色泽": ["青绿", "乌黑", "乌黑", "青绿", "乌黑", "青绿", "浅白", "乌黑", "浅白", "青绿","青绿", "浅白", "乌黑", "乌黑", "浅白", "浅白", "青绿", "乌黑", "青绿", "浅白","乌黑", "青绿", "浅白", "乌黑", "青绿", "浅白", "乌黑", "青绿", "浅白", "乌黑"],"根蒂": ["蜷缩", "蜷缩", "蜷缩", "稍蜷", "稍蜷", "硬挺", "稍蜷", "稍蜷", "蜷缩", "蜷缩","蜷缩", "蜷缩", "稍蜷", "稍蜷", "硬挺", "蜷缩", "稍蜷", "蜷缩", "稍蜷", "硬挺","蜷缩", "稍蜷", "蜷缩", "稍蜷", "硬挺", "稍蜷", "蜷缩", "稍蜷", "硬挺", "稍蜷"],"敲声": ["浊响", "沉闷", "浊响", "浊响", "浊响", "清脆", "沉闷", "浊响", "浊响", "沉闷","沉闷", "浊响", "浊响", "沉闷", "清脆", "浊响", "浊响", "沉闷", "浊响", "清脆","浊响", "浊响", "沉闷", "浊响", "清脆", "沉闷", "浊响", "浊响", "清脆", "沉闷"],"纹理": ["清晰", "清晰", "清晰", "清晰", "稍糊", "清晰", "稍糊", "清晰", "模糊", "稍糊","清晰", "清晰", "清晰", "稍糊", "模糊", "模糊", "稍糊", "清晰", "清晰", "模糊","清晰", "稍糊", "清晰", "稍糊", "清晰", "稍糊", "清晰", "稍糊", "清晰", "稍糊"],# 数值特征（模拟好瓜关键属性，已标准化前处理）"糖度": np.random.normal(loc=[6.0, 4.0], scale=0.8, size=30).round(2),  # 好瓜糖度更高"酸度": np.random.normal(loc=[2.5, 3.5], scale=0.6, size=30).round(2),  # 好瓜酸度更低# 标签（1=好瓜，0=坏瓜）"好瓜": [1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0,1, 1, 0, 1, 0, 0, 1, 1, 0, 0]
}# 转换为DataFrame格式
df = pd.DataFrame(good_melon_data)# 查看数据集基本信息
print("数据集形状（样本数, 特征数）：", df.shape)  # 30个样本，6个特征（含标签前5个）
print("\n数据集前5行：")
print(df.head())
print("\n好瓜/坏瓜样本分布：")
print(df["好瓜"].value_counts())

3. 数据预处理（分类特征编码 + 数值特征标准化）

神经网络对输入数据格式和量纲敏感，需将文本特征转为数值，数值特征标准化（消除量纲干扰）：

# 1. 分离特征（X）与标签（y）
X = df.drop("好瓜", axis=1)
y = df["好瓜"].values.reshape(-1, 1)  # 转为列向量，适配神经网络输出维度# 2. 分类特征编码（LabelEncoder）
label_encoders = {}
for col in ["色泽", "根蒂", "敲声", "纹理"]:le = LabelEncoder()X[col] = le.fit_transform(X[col])label_encoders[col] = le  # 保存编码规则（如：色泽-青绿=0，乌黑=1）# 3. 数值特征标准化（糖度、酸度）
scaler = StandardScaler()
X[["糖度", "酸度"]] = scaler.fit_transform(X[["糖度", "酸度"]])# 4. 划分训练集（70%）与测试集（30%）
X_train, X_test, y_train, y_test = train_test_split(X.values, y, test_size=0.3, random_state=42, stratify=y
)# 查看预处理后的数据
print("\n预处理后训练集形状：", X_train.shape)  # (21, 6)：21个样本，6个输入特征
print("预处理后测试集形状：", X_test.shape)    # (9, 6)：9个样本，6个输入特征
print("训练集标签形状：", y_train.shape)      # (21, 1)：21个样本，1个输出标签

4. 手动实现全连接神经网络（核心代码）

定义神经网络类，包含 “权重初始化”“激活函数”“前向传播”“反向传播”“模型训练” 核心功能：

class SimpleFullyConnectedNN:def __init__(self, input_dim, hidden_dim, output_dim, learning_rate=0.01):"""初始化全连接神经网络参数：input_dim: 输入特征维度（如6：6个好瓜特征）hidden_dim: 隐藏层神经元数量（经验值，如8）output_dim: 输出维度（二分类任务设为1）learning_rate: 学习率（控制参数更新幅度，默认0.01）"""# 1. 初始化权重和偏置（随机初始化，服从正态分布）# 输入层→隐藏层：权重shape=(input_dim, hidden_dim)，偏置shape=(1, hidden_dim)self.W1 = np.random.normal(loc=0, scale=0.1, size=(input_dim, hidden_dim))self.b1 = np.zeros((1, hidden_dim))  # 偏置初始化为0# 隐藏层→输出层：权重shape=(hidden_dim, output_dim)，偏置shape=(1, output_dim)self.W2 = np.random.normal(loc=0, scale=0.1, size=(hidden_dim, output_dim))self.b2 = np.zeros((1, output_dim))# 2. 超参数设置self.lr = learning_rateself.loss_history = []  # 记录训练过程的损失值，用于可视化def sigmoid(self, z):"""激活函数：sigmoid（将输出映射到0-1，适合二分类）"""# 避免z过大导致exp(-z)下溢，添加数值稳定处理z = np.clip(z, -500, 500)return 1 / (1 + np.exp(-z))def sigmoid_derivative(self, a):"""sigmoid函数的导数（用于反向传播计算梯度）"""# a是sigmoid的输出，导数公式：a*(1-a)return a * (1 - a)def forward_propagation(self, X):"""前向传播：计算预测结果参数：X: 输入数据（shape=(样本数, input_dim)）返回：hidden_out: 隐藏层输出，output: 输出层预测结果"""# 1. 输入层→隐藏层：z1 = X*W1 + b1，hidden_out = sigmoid(z1)self.z1 = np.dot(X, self.W1) + self.b1self.hidden_out = self.sigmoid(self.z1)# 2. 隐藏层→输出层：z2 = hidden_out*W2 + b2，output = sigmoid(z2)self.z2 = np.dot(self.hidden_out, self.W2) + self.b2self.output = self.sigmoid(self.z2)return self.hidden_out, self.outputdef compute_loss(self, y_true, y_pred):"""计算损失：二分类交叉熵损失（比均方误差更适合分类任务）"""# 避免log(0)或log(1)导致数值错误，添加微小值y_pred = np.clip(y_pred, 1e-10, 1 - 1e-10)loss = -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))return lossdef backward_propagation(self, X, y_true):"""反向传播：计算参数梯度并更新权重和偏置参数：X: 输入数据，y_true: 真实标签"""# 1. 计算输出层误差（y_true - y_pred）与梯度m = X.shape[0]  # 样本数量output_error = y_true - self.output  # 输出层误差（shape=(m, 1)）# 输出层权重W2的梯度：hidden_out.T * (output_error * sigmoid_derivative(output))dW2 = np.dot(self.hidden_out.T, output_error * self.sigmoid_derivative(self.output)) / m# 输出层偏置b2的梯度：均值化误差（因偏置对每个样本的影响相同）db2 = np.mean(output_error * self.sigmoid_derivative(self.output), axis=0, keepdims=True)# 2. 计算隐藏层误差与梯度（误差反向传递）# 隐藏层误差：(output_error * sigmoid_derivative(output)) * W2.Thidden_error = np.dot(output_error * self.sigmoid_derivative(self.output), self.W2.T)# 隐藏层权重W1的梯度：X.T * (hidden_error * sigmoid_derivative(hidden_out))dW1 = np.dot(X.T, hidden_error * self.sigmoid_derivative(self.hidden_out)) / m# 隐藏层偏置b1的梯度：均值化隐藏层误差db1 = np.mean(hidden_error * self.sigmoid_derivative(self.hidden_out), axis=0, keepdims=True)# 3. 更新权重和偏置（梯度下降：参数 = 参数 - 学习率×梯度）self.W1 += self.lr * dW1self.b1 += self.lr * db1self.W2 += self.lr * dW2self.b2 += self.lr * db2def train(self, X_train, y_train, epochs=1000, print_interval=100):"""模型训练：迭代执行前向传播、损失计算、反向传播参数：X_train: 训练集特征y_train: 训练集标签epochs: 训练迭代次数（默认1000）print_interval: 每多少轮打印一次训练信息（默认100）"""for epoch in range(1, epochs + 1):# 1. 前向传播计算预测结果_, y_pred_train = self.forward_propagation(X_train)# 2. 计算训练损失train_loss = self.compute_loss(y_train, y_pred_train)self.loss_history.append(train_loss)# 3. 反向传播更新参数self.backward_propagation(X_train, y_train)# 4. 定期打印训练信息if epoch % print_interval == 0:# 计算训练精度（预测值>0.5视为1，否则视为0）train_pred = (y_pred_train > 0.5).astype(int)train_acc = accuracy_score(y_train.astype(int), train_pred)print(f"Epoch {epoch:4d} | 训练损失：{train_loss:.4f} | 训练精度：{train_acc:.4f}")def predict(self, X):"""模型预测：输入数据，输出预测标签（0或1）"""_, y_pred = self.forward_propagation(X)return (y_pred > 0.5).astype(int)  # 二分类阈值设为0.5

5. 模型训练与测试（好瓜分类任务）

初始化神经网络，设置超参数，执行训练并验证测试集效果：

# 1. 初始化全连接神经网络
# 输入维度=6（6个好瓜特征），隐藏层神经元=8（经验值），输出维度=1（二分类）
nn_model = SimpleFullyConnectedNN(input_dim=X_train.shape[1],hidden_dim=8,output_dim=1,learning_rate=0.05  # 调整学习率，加速收敛
)# 2. 训练模型（迭代1000轮，每100轮打印信息）
print("\n开始训练全连接神经网络...")
nn_model.train(X_train, y_train, epochs=1000, print_interval=100)# 3. 测试集预测与评估
y_test_pred = nn_model.predict(X_test)
test_acc = accuracy_score(y_test.astype(int), y_test_pred)
test_loss = nn_model.compute_loss(y_test, nn_model.forward_propagation(X_test)[1])# 输出测试集结果
print("\n" + "="*50)
print("全连接神经网络测试集评估结果")
print("="*50)
print(f"测试集损失：{test_loss:.4f}")
print(f"测试集精度：{test_acc:.4f}")
print("\n测试集分类报告：")
print(classification_report(y_test.astype(int), y_test_pred,target_names=["坏瓜", "好瓜"],zero_division=0  # 避免无预测样本时的警告
))

6. 结果可视化（训练损失曲线 + 精度对比）

通过图表直观展示模型训练过程的损失变化，以及训练集 / 测试集精度对比：

# 设置中文字体（避免中文乱码）
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False# 创建画布（1行2列，左侧损失曲线，右侧精度对比）
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))# 1. 训练损失曲线（左侧子图）
ax1.plot(range(1, len(nn_model.loss_history)+1), nn_model.loss_history, color='#2E86AB', linewidth=2, label='训练损失')
ax1.set_xlabel("训练迭代次数（Epoch）", fontsize=12)
ax1.set_ylabel("交叉熵损失值", fontsize=12)
ax1.set_title("神经网络训练损失变化曲线", fontsize=14)
ax1.legend()
ax1.grid(alpha=0.3)# 2. 训练集/测试集精度对比（右侧子图）
# 计算训练集精度
y_train_pred = nn_model.predict(X_train)
train_acc = accuracy_score(y_train.astype(int), y_train_pred)
# 测试集精度（已计算）
accs = [train_acc, test_acc]
labels = ["训练集", "测试集"]
colors = ['#A23B72', '#F18F01']# 绘制柱状图
bars = ax2.bar(labels, accs, color=colors, alpha=0.8, edgecolor='black', linewidth=1)
# 添加数值标签
for bar, acc in zip(bars, accs):height = bar.get_height()ax2.text(bar.get_x() + bar.get_width()/2., height + 0.01,f'{acc:.4f}', ha='center', va='bottom', fontsize=12, fontweight='bold')ax2.set_ylabel("分类精度", fontsize=12)
ax2.set_title("神经网络训练集与测试集精度对比（好瓜分类）", fontsize=14)
ax2.set_ylim(0.5, 1.05)  # 调整y轴范围，突出差异
ax2.grid(axis='y', alpha=0.3)# 调整子图间距，保存图片（可直接插入CSDN推文）
plt.tight_layout()
plt.savefig("simple_nn_melon_classification.png", dpi=300, bbox_inches='tight')
plt.show()

三、代码使用说明与结果解读

1. 代码适配性

超参数调整：若训练损失下降缓慢，可增大learning_rate（如 0.05→0.1）；若损失震荡不收敛，可减小学习率或增加hidden_dim（如 8→12）；
数据集替换：若用自定义数据集，需确保输入特征维度input_dim与数据匹配（如 10 个特征则input_dim=10），二分类任务output_dim固定为 1。

2. 关键结果解读

训练损失曲线：随着迭代次数增加，损失值应逐渐下降并趋于平稳（如从 1.0 降至 0.2 以下），说明模型在持续学习；若损失不降反升，需检查学习率或权重初始化；
精度对比：训练集精度通常高于测试集（正常现象），若两者差异过大（如训练集 1.0、测试集 0.6），可能存在过拟合，可减少hidden_dim或增加训练样本；
业务意义：模型能通过 “根蒂、纹理” 等关键特征的权重学习，自动识别好瓜特征，证明神经网络可通过数据 “自主学习” 分类规律，无需手动设计规则。

查看全文

http://www.dtcms.com/a/501367.html